基于城乡公交网络的小件快运路径选择

申 科，赵建有，康 静 SHEN Ke,ZHAO Jianyou,KANG Jing

（1.长安大学 汽车学院，陕西 西安 710064；2.中南大学 交通运输工程学院，湖南 长沙 410075）

0 引言

近几年，小件快运成为大多数客运企业实现经济增长和转型发展的手段之一[1]。同样地，城乡公交企业也可以利用自己平时较大的空载空间发展小件快运，在满足农村居民出行需求的同时，还可以满足农村居民在日常生产生活中对小件物品日益增长的需求[2]。目前专业的快递公司均受限于农村快运市场点多、面广、偏远以及与市区路况相差很大的特点，致使农村物流市场发展迟缓，而利用城乡公交发展小件快运便可以在一定程度上加快城乡物流以及农村物流市场的发展。因此，城乡公交小件快运的路径选择是否科学、合理是至关重要的[3]。

由于小件快运起步较晚，因此，目前国内外学者对小件快运的研究成果并不是很多，其主要研究成果有：赖平仲对小件快运的市场环境进行分析，其研究结果表明公路小件快运在农村市场发展前景最大[4]。刘莹对小件快运企业运输模式进行研究，最后分析归纳得出小件快运企业的运输模式主要为专线物流、联盟运输、单一运输这三种模式[5]。郑昌旭对小件快运的网络结构和时空特性进行分析，建立了服务网络设计模型，并结合案例给出了详细的小件快运服务网络设计方案[6]。赵锋超对小件快运在农村市场发展的有利条件和不利条件进行分析，提出了一系列促进小件快运发展的措施[7]。夏跃华以小件快运运输总时间最短为目标，构建了小件快运的车辆调度模型，并结合实例得出运输时间最短的车辆调度方案[8]。梁娜、高冲等以小件快运运输总成本最小为目标，构建了小件快运运输路径选择模型，并结合实例得出运输成本最小的运输路径选择方案[9]。梁娜针对小件快运路径选择问题展开研究，依据运输目标的优先顺序建立了多目标动态规划模型，并结合实例运用模型和LINGO软件求解出了最佳运输路线方案[10]。刘如意对乡镇客运站小件快运业务运营现状进行调研，总结了运营过程中的一些不足之处，并提出相关建议[11]。 Nicolas Teypaz等人以小件快运企业所获经济效益最大为目标，构建了小件快运运输服务网络模型[12]。Ferdinand Friska Natalia以快递收发效率最大为目标，建立一种小件快运企业收发快递最快的服务模式[13]。Yuan Cai和Jinhua Chen分析了综合城乡区域的终端物流配送方法，并对城乡一体化的最终布局的方法进行了讨论[14]。 Heechul Bae等人以运输总成本最小为目标，引入服务时间软约束，建立了多站点带时间窗的车辆路径优化模型[15]。

综观上述研究现状，学者们多数只依托道路客运企业对小件快运进行研究，而很少依托城乡公交研究小件快运的，这主要是因为之前我国城乡公交发展滞后，而自国家提出乡村振兴战略和“四好农村公路”以来，我国城乡公交获得了很快的发展，为开展小件快运提供了基础。因此基于城乡公交网络对小件快运的路径选择进行研究显得尤为重要。

1 基于城乡公交网络的小件快运路径选择模型

1.1 模型假设

城乡公交小件快运路径选择的实质是在已有的多条城乡公交路线中选择一条效率高、经济性好的运输路线。建模之前需明确模型的适用条件，即基本假设如下[16]：（1）城乡公交小件快运的各运输目标相互独立、互不影响。（2）城乡公交车的车辆参数（包括车型、限载乘客、体积、行李舱容积等）和运营参数（包括行驶速度、运营时刻表、公交班次等）全部相同。（3）城乡公交车辆在小件运输途中除运输距离和运输货物的质量外，其他影响运输费用的因素保持不变，如油价、车损等。（4）快运小件没有优先顺序，按先到先装车、先运走的原则进行装载，装载的小件最大不超过行李舱最大容量和最大载重量，运输实行按件数收费。（5）不考虑道路状况对城乡公交车行驶的影响，不考虑拥堵、自然灾害、交通事故等意外因素的发生。

1.2 参数说明

该模型涉及到的参数有[17]：i：始发站编号，i=1,2,…,n；j：到达站编号，j=1,2,…,n,且i≠j；G：客车行李舱最大载重量（kg）；V：客车行李舱最大容量限制（m）3；g：站点i装入行李舱的货物质量（kg）；V：站点i装入行李舱的货物体积（m）3；

mii k：客车班次，由i点发往j点的第k辆客车，其中k=1,2,…,m；M：客车班次集合，一条线路上的客车班次数，假设车辆型号、装载限制相同，M=｛1,2 ,…,m｝；tij：从i点到j点客车按规定路线行驶的在途运行时间（min），不含停靠时间，tij≥0；：从i点到j点客车在每个固定停靠站停留的时间（min），≥0；xij：从i点到j点的固定停靠站数目（只针对直达线路）；Z1：运输时间的目标函数；cij：i到j点之间运送单位距离单件货物的费用（元/件·km）；lij：站点i到站点j的实际道路长度（km）；yij：在i点装车被运送到j点的货物总件数（件）；Z2：运输成本的目标函数；ph：运输目标的重要程度，即优先因子，h＝1,2，规定优先因子为p1的运输目标应比优先因子为p2的运输目标先得到满足，且ph的取值越大，目标的重要程度越高，应先被满足，ph值的确定需根据专家打分法和未来规划而量化；p1：最短运输时间目标的优先因子，即规划运输路线时首先考虑满足最短运输时间，其次考虑其他目标；p2：最低运输成本目标的优先因子，即在满足最短运输时间的情况下再考虑最低运输成本目标的实现；wh：不同重要程度下运输目标归一化处理的单位参考值，为常数。为方便分析，这里将所有量纲都统一转化为时间（min）来进行分析；w1：最短运输时间目标归一化处理的单位参考值，这里将所有量纲都统一转化为时间（min），因此w1取值为1，无单位；w2：最低运输成本目标归一化处理的单位参考值，这里将所有量纲都统一转化为时间（min），因此w2的单位是元/分钟；Z：小件快运整体目标规划的函数。

决策变量：

1.3 模型构建

1.3.1 最短运输时间目标的建模

小件快运的运输时间在所有目标中是重视程度最高的，应先得到满足，主要包含客车在途运行时间和在固定停靠站停留时间。在城镇公交干线和镇村公交支线上均设有固定停靠站和简易招呼站，为沿线镇、村的居民提供便利的公交服务，因此必须考虑该部分时间对运输小件的影响[18]。但是由于该时间随机性较大，无法具体测量，为方便建立模型，将每次停靠时间视为固定常量，总的停靠时间还要考虑停靠站的个数。在此，把在途运行时间和停靠时间作为变量建模，最短运输时间目标的数学模型如下：

1.3.2 最低运输成本目标的建模

成本一直是小件快运相对专业的物流公司所具备的优势，应着重发挥。这里考虑了三个关键变量：单位质量单位距离的运费、两站点间货物质量和两站点间实际道路长度。为简化问题，将所有小件看作标准件（根据道路客运小件快运服务规范要求，定义体积在0.4*0.5*0.5m3以内，质量30kg以内的小件为标准小件）[19]。最低运输成本目标的数学模型如下：

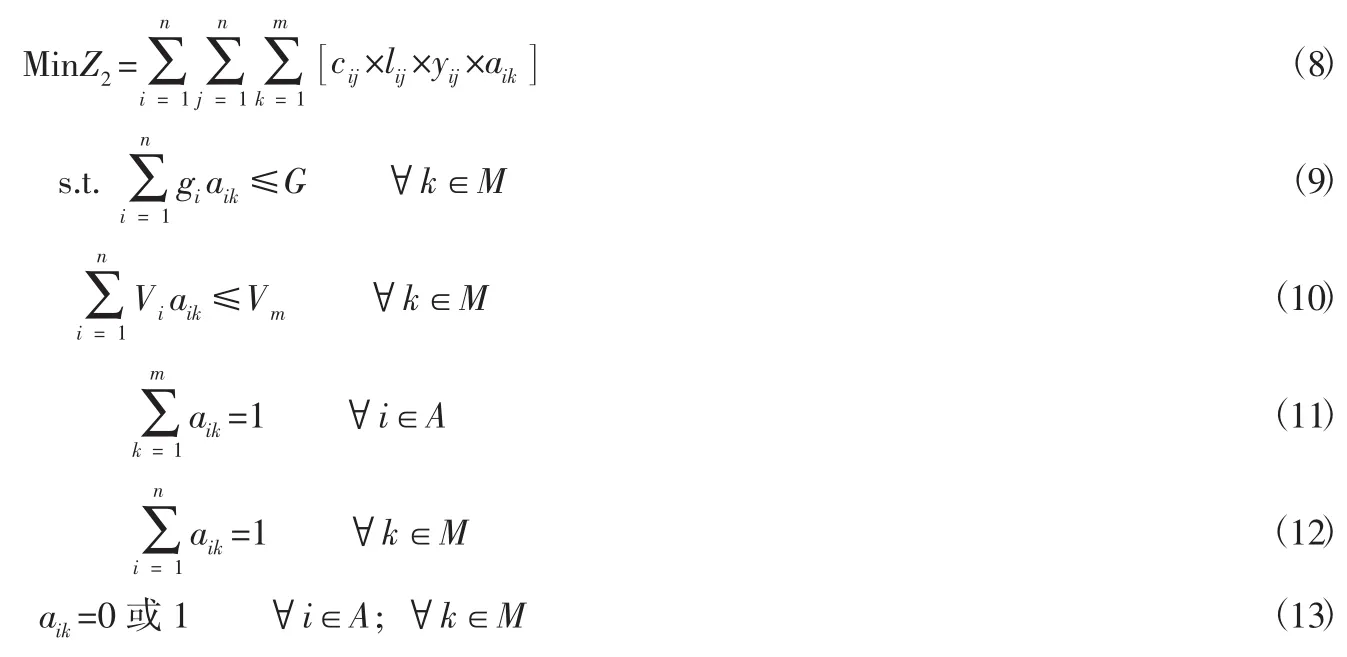
1.3.3 整体目标规划分析与建模

在建模之前，由调研数据可得，客运企业小件快运运输路线的规划应按照最短运输时间、最低运输成本的目标满足顺序来进行[20]。本文所建模型为含有两个小指标的目标规划转化为整体目标规划的路线选择模型。总目标规划模型如下：

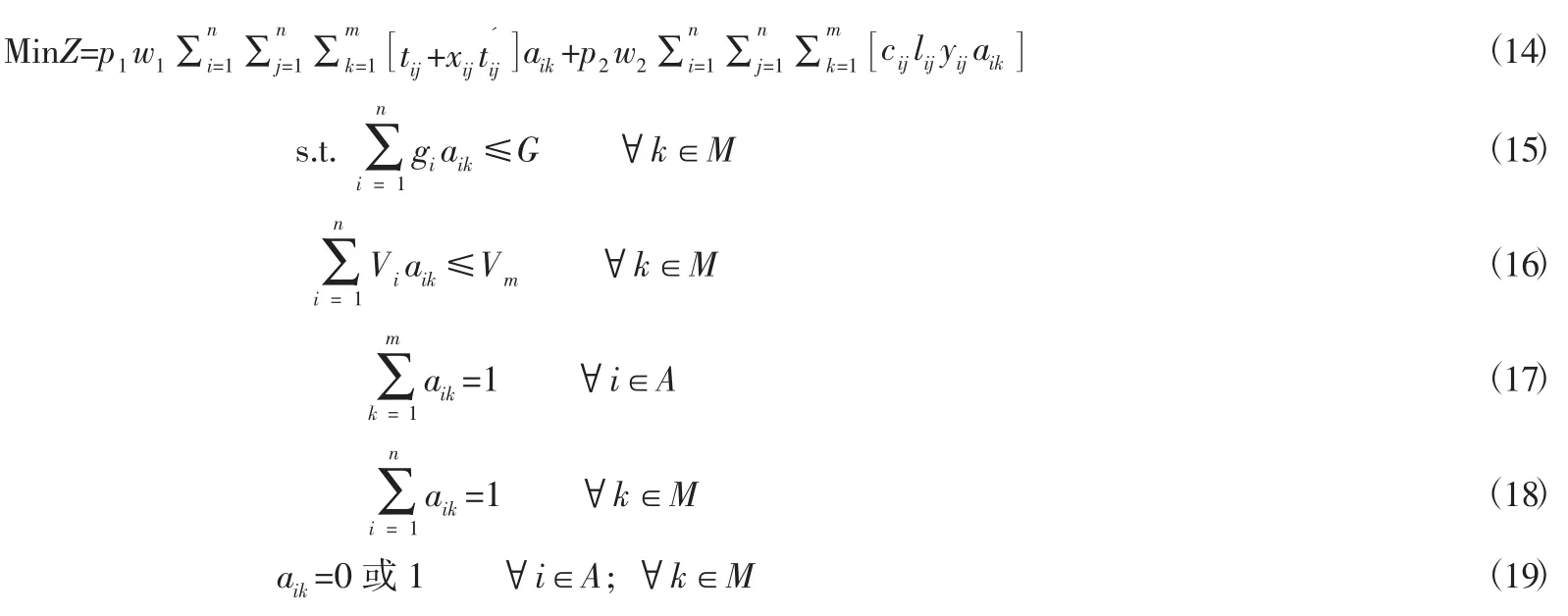
2 案例分析

2.1 案例介绍

近年来，渭南市华州区的城乡公交发展迅速，其城乡公交运营的车辆数已有100辆，这为小件快运业务的开展奠定了基础。现以渭南市华州区县城到北拾村的城乡公交线网为研究对象，对小件快运路径选择进行研究以更好地开展小件快运业务。根据这个区域包含的镇、村的地理位置（如图1所示），列出10个重要的运输网络站点，这些站点对应的名称如表1所示，构建出这些站点间的运输路线网络如图2所示。

各运输站点之间的实际道路长度lij（只包括直达线路）和各条线路上的固定停靠点个数xij（只针对直达线路）等信息如表2所示。

对于货物需求量，则根据各个镇、村近年的人口数，得到各运输站点间的日均小件流量，如表3所示。本文并未对快运小件进行分类统计，为此，采集数据为综合统计量，不区分货类差异。

小件快运业务都是利用客运站的客运班车的行李舱进行“捎带运输”，客车的车型主要采用车长为5.99米的南京金龙纯电动开沃客车NJL6600，其额定总质量为6 800kg（带空调状态），行李舱的容积为0.84m3，假设乘客行李所占空间不到行李舱容积的三分之一[20]，剩余的仓容为0.56m3，如果每个小件按0.01m3折算，则剩余行李舱的最大运送能力为56件/班次。

2.2 案例说明

现要规划从站点1到站点10的最优快运路线，依据运输目标的优先顺序，应先选择运输时间最短的路线，如果有多条最短运输时间的线路，则比较各条线路的运输成本，最后综合考虑两个指标，选择出最佳运输路线方案。针对该案例的模型基本适用条件如下：（1）在每个固定停靠点均会停留且停留时间取2分钟；（2）营运客车的平均行驶速度为25km/h，视其固定不变[10]；（3） 客运站发车时间为6：30～19：30，发车频率按30分钟计，则每条线路的发车班次k为26次；（4） 各运输站点间的小件快运容量为56×26=1 456（件）；（5） 单位小件运输成本为0.05元/件公里[9]；（6）p1、p2分别是最短运输时间和最低运输成本的优先因子，结合实际情况，对p1和p2按权重比例分别取值为55.9%和44.1%；（7） 按实地调研情况对w1取1，w2取0.63 元/分钟。

2.3 案例求解

图1 华州区县城到北拾村之间各村镇的地理位置

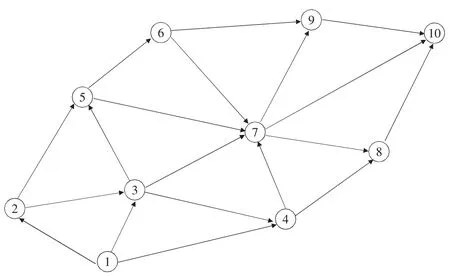
图2 运输站点路网图

表1 路网编号对应站点

表2 各运输站点之间的基本信息

上述案例的数学模型中，最短运输时间和最低运输成本这两个目标优化的结果需要运用LINGO软件求解。依据运输目标的优先顺序，具体的求解结果如下：（1）先求解运输时间最短的路线。运输时间包括在途运行时间和固定停靠时间，由于已知各运输站点间的固定停靠点个数且停留时间视为常数，则将这两段时间求和，再利用LINGO软件规划时效性最高的路径。求解结果为最短运输时间为45分钟，相对应的路径为1-4-8-10。（2）如果有多条满足最短运输时间的路线，则继续比较各条路线的运输成本，从而选出成本最低的路线。但是第一步中只得到一条最短运输时间的路径，因此还需要比较该路径与其他路径的运输成本，求解结果为最低运输成本23.19元，相对应的路径为1-3-7-9-10。（3）目前依据两个不同的指标求解出两条分别符合单目标的运输路线，因此需要引入权重值ph和量纲wh来衡量哪条路线最符合小件快运的运输要求，使得总的效用值最小。求解结果为最佳运输路线1-4-8-10，目标函数值为34.59元，路线图如图3所示。

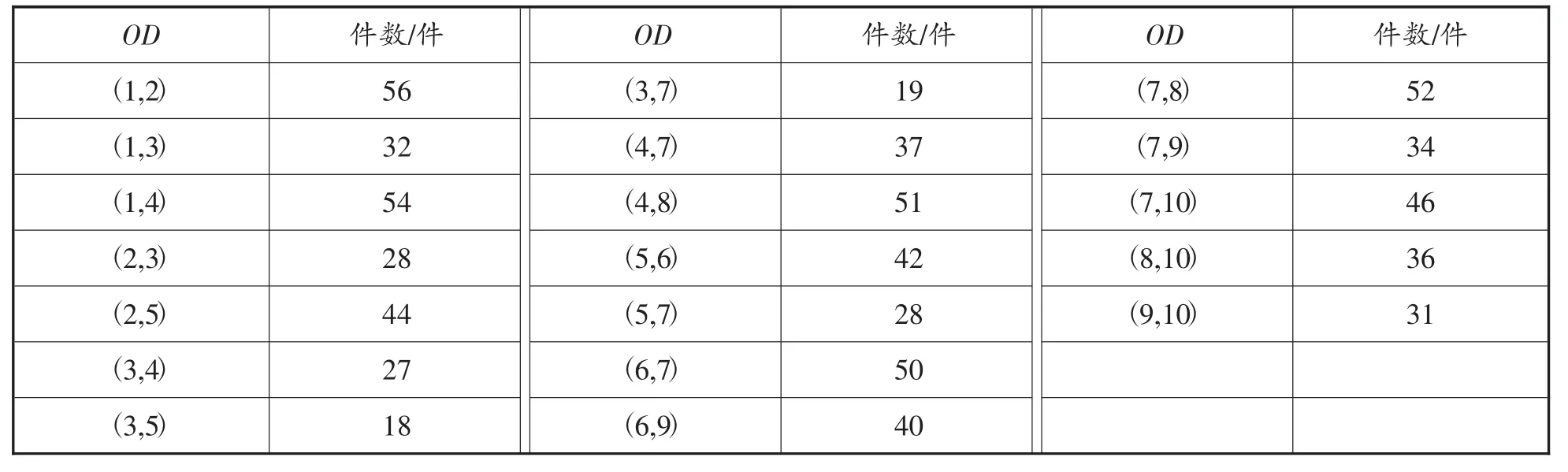
表3 各运输站点之间的日均小件流量

图3 最佳运输路线网络图

3 结论

本文在实地考察和查阅大量资料的基础上，确定了运输目标的优先顺序，即时效性和低成本是必须被重视的优势。故以最短运输时间和最低运输成本作为两个单目标，主要约束条件为客车行李舱的装载和容量限制，用 0-1变量表示客运小件的装载和运送状态，应用运筹学中目标规划的方法分别对两个单目标和整体运输目标建立模型。结合渭南市华州区城乡客运站的实际情况，选取了10个运输网络站点并构建出路线图进行路线选择的分析，再运用所建模型和LINGO软件规划出符合运输目标优先顺序的最佳运输路线方案，验证了模型的有效性，解决了客运站开展小件快运业务的实际问题。