LBM中基于半程反弹的统一边界条件研究

凌风如，张超英，陈燕雁，覃章荣

(广西师范大学 广西多源信息挖掘与安全重点实验室，广西 桂林 541004)

近年来，格子Boltzmann方法(lattice Boltzmann method，简称LBM)在流体力学中备受关注，它用简单的微观动力学模型模拟复杂的宏观现象，具有算法简单、边界实现容易、并行度高等优点[1-6]。LBM现已广泛应用于流体力学的众多方面，如湍流、多相流、空气动力学、磁流体力学以及一些化学反应和具有复杂边界的流体流动。对于计算流体力学中的问题，边界处理极其重要，它将影响模拟结果的精度和稳定性，因此边界处理一直是人们研究的热点。

反弹格式是处理静止无滑移平直边界的一类常用且简单的方法。在该格式中，边界点分布函数的流出方向被简单地设定为流入方向的反向[7-8]。在LBM模拟中，存在2种类型的反弹格式，即全程反弹和半程反弹[9]。在全程反弹方案中，物理边界位于格子点上；在半程反弹方案中，物理边界位于格子点中间，前者只有一阶精度，后者在空间上具有二阶精度[7]。但是，反弹格式的处理方法并不能精准地模拟曲线边界[10]。为了提高基于反弹方案的阶梯逼近格式的计算精度，人们提出曲线边界处理方法以解决复杂的几何边界问题。第一种曲线边界处理方法是由Filippova和Hänel提出的(以下简称为FH格式)[11-12]。该方法采用一种虚平衡分布函数，基于分布函数插值构建了具有二阶精度的边界条件。然而，它的数值稳定性较差，特别是当近边界流体点非常接近固壁边界时。为了提高FH格式的数值稳定性，Mei等[13-14]提出了一种改进的曲线边界处理方法。Bouzidi等[15]提出了一种具有二阶精度的曲线边界处理方法，该方法结合了流体点分布函数的线性或二次插值和反弹技术。Lallemand等[16]改进了这种方法，并将其扩展到运动边界中。Yu等[17]通过使用2次顺序插值的方法提出一种统一的曲线边界处理方法，解决了以上边界处理的不连续性问题。Tao等[18]提出一种基于单点的曲线边界处理方法，该方法结合了插值和非平衡态外推技术，能充分实现LBM的并行计算优势。后来，学者们又进一步改进了这些边界处理方法[19-21]。

在LBM模拟中，使用基于插值或外推的曲线边界处理方法时，系统的质量守恒通常难以保证，在模拟的每个时步都存在质量的损失或增加，被称为“质量泄漏”。Lallemand等[16]认为使用插值的方法会打破曲线边界附近的质量守恒。为了解决质量泄漏的问题，学者们提出基于流量的有限体积格式的曲线边界处理方法，这无疑增加了LBM计算的复杂性[22]。随后，学者们提出了多种质量守恒的曲线边界处理方法以达到避免质量泄漏和提高数值稳定性的效果，但这些边界处理方法仍存在轻微的质量泄漏问题[23]。不过，在实际的LBM模拟中考虑到计算精度、易操作性和可靠性这3个因素，在求解曲线边界问题上，插值技术仍受到大多数学者们的青睐。基于此，本文提出一种质量守恒的统一曲线边界处理方法，并使用经典算例分别验证该方法的计算精度、数值稳定性和质量守恒。

本文内容安排如下：第1节简要回顾单弛豫的Bhatnagar-Gross-Krook (BGK)近似的格子Boltzmann方法的基本原理和文献中常用的曲线边界处理方法；第2节介绍本文提出的一种质量守恒的统一曲线边界处理新方法；第3节以Poiseuille流为例，验证本文提出的统一曲线边界条件的有效性，并与常用的边界条件进行比较；第4节总结本文提出的曲线边界方法的特点。

1 格子Boltzmann方法和曲线边界条件

单弛豫时间近似的LBM模型(LBGK)的演化方程为[7]：

(1)

(2)

(3)

标准的LBM演化过程分为碰撞和流动2个步骤，分别是：

(4)

(5)

(6)

在图1中，当q取值为0.5或1时，粒子分布函数以速度ei从近边界流体点xf处流动到物理边界，接着以速度e-i反弹到xf处，这就是标准的反弹格式；但当q取其他值时，离开近边界流体点xf处的粒子经历反弹后，并未回到xf处，因此需要专门的处理。

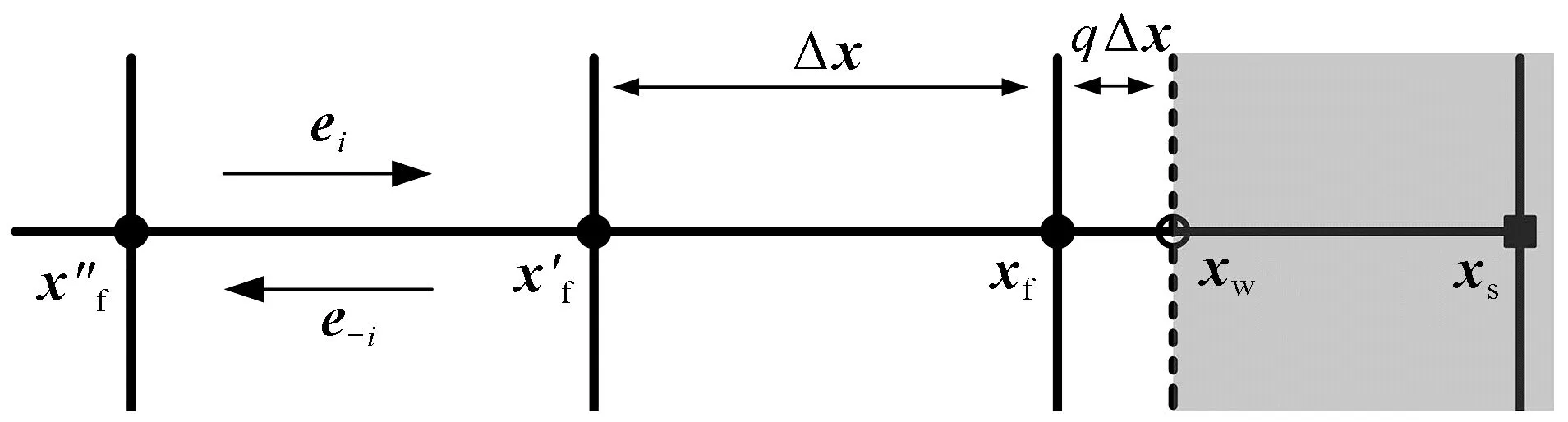
图1 规则格子和曲线边界的一维投影Fig.1 1D projection of regular lattice and curved boundary

(7)

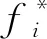
(8)

其中，uf=u(xf，t)是近边界流体点xf处的流体速度，usf是一个待定的虚拟速度，c=δx/δt=1。Filippova和Hänel考虑到缓慢流动因素，对uf在xw处作Taylor展开后进行化简，提出用以下关系式来确定usf和χ：

(9)

(10)

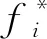
(11)

(12)

当弛豫时间τ取值较小时，Mei等改进的公式可获得较好的稳定性，但是当τ>1.25时其仍然可能存在发散的问题[24]。除此之外，Mei等[25]还将改进的格式(以下简称为MLS格式)推广到三维空间应用。

对于无滑移的物理边界，利用反弹的方法进行处理是最简单和容易实现的，因此在LB模拟中被广泛使用。Bouzidi等[15]提出了一种结合反弹和插值的曲线边界处理方法(以下简称BFL格式)。该格式的计算公式为：

(13)

(14)

在之后的研究中，Lallemand和Luo[16]应用相同的方法改进了BFL格式，即在引用插值公式时，把所有的分布函数统一到同一个时间层次上，同时考虑碰撞和流动步骤(以下简称LL格式)。LL格式中边界未知分布函数的计算公式为：

(15)

(16)

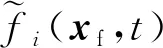
(17)

可以证明上述线性插值得到的YMS1格式具有二阶精度。同时可使用高阶插值得到更高精度的YMS2格式[24]：

(18)

从式(17)和(18)可以看出，YMS1格式和YMS2格式在处理曲线边界时不需要区分q的大小。然而，与其他格式相比，YMS格式需要涉及更多的操作和临近边界流体点的分布函数，这在某种程度上会影响LBM数值模拟的并行计算优势。

Tao等[18]提出了一种基于单点的二阶精度的曲线边界处理方法(以下简称TAO格式)。TAO格式边界处未知分布函数的计算公式为：

(19)

从其计算公式可以看出，该格式仅利用近边界流体点xf处的分布函数。TAO格式使用了插值、非平衡外推和时空近似等方法，得到了一种基于单点的二阶精度的曲线边界处理方法，该方法能够充分发挥LBM数值模拟的并行计算优势。

2 基于半程反弹的统一边界条件

(20)

最后利用t+δt时刻的分布函数f-i(xv，t+δt)和f-i(x′f，t+δt)插值，即可求得边界处待求的分布函数f-i(xf，t+δt)。

(21)

代入式(20)得f-i(xv，t+δt)，再进行插值得：

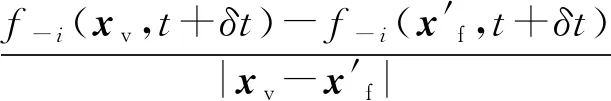
(22)

即可求得：

(23)

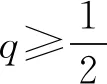
(24)

(25)

其中，α是一个与τ有关的修正因子，用于减小插值带来的误差，由拟合Poiseuille流的数据确定，形式如下：

(26)

图2 HBI格式示意图Fig.2 Schematic of HBI model

3 模拟计算结果

在本文的研究中，通过2种经典的Poiseuille流算例，一种是常规的Poiseuille流，另一种是给流场施加恒定重力，分别验证本文提出的HBI格式的计算精度、数值稳定性和质量守恒。然后将使用HBI格式获得的结果与FH格式、MLS格式、BFL格式、LL格式、YMS1格式、YMS2格式和TAO格式分别进行比较。

3.1 验证边界条件的精度和稳定性

为了验证HBI格式计算精度和数值稳定性，我们采用FH格式、MLS格式、BFL格式、LL格式、YMS1格式、YMS2格式、TAO格式及HBI格式处理不同位置的固壁边界对Poiseuille流进行模拟。流场左右使用周期边界，以恒定压力作为体力驱动流场内分布函数运动，其实现形式如下：

(27)

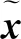
(28)

其中，ν为粘滞系数，h为流场高度，b=y/h。由图3可得，使用HBI格式模拟的结果u(y)与理论值uex(y)精确重合，证明本文提出的统一曲线边界条件是可靠的。

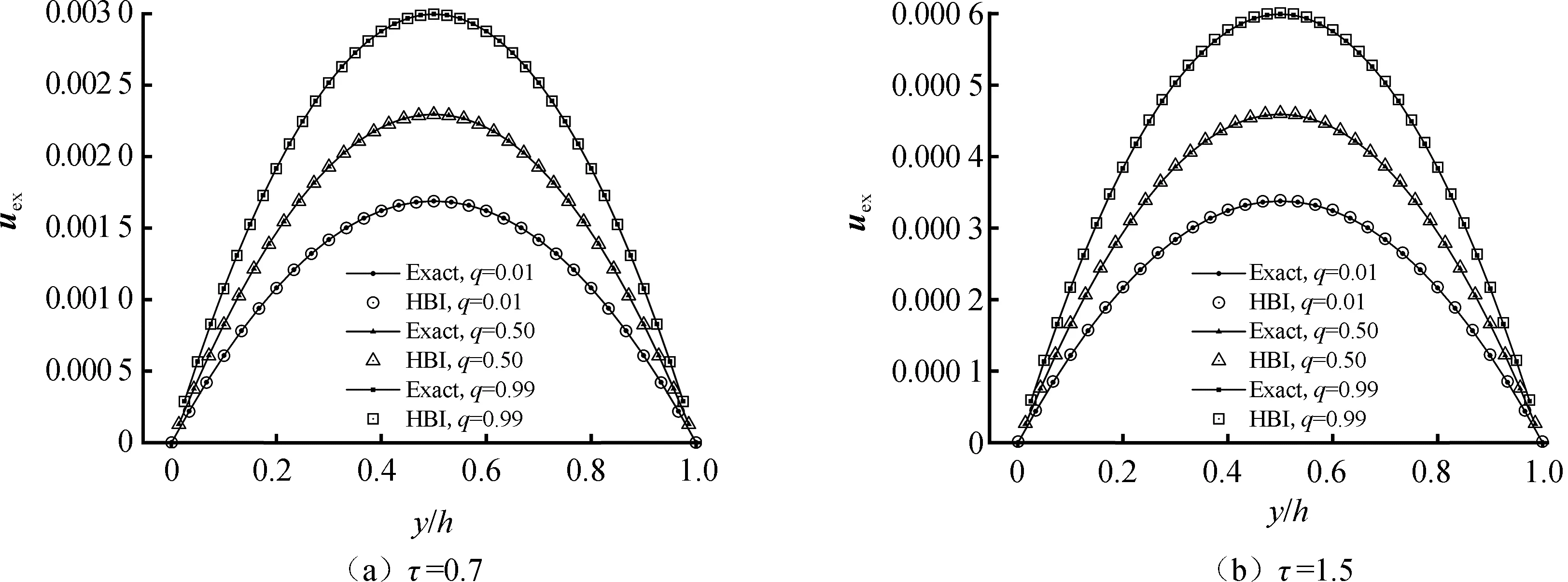
图3 使用HBI格式模拟Poiseuille流的结果Fig.3 Simulations of Poiseuille flow using HBI model

为了定量地对比HBI和其他曲线边界条件，定义u(y)的相对L2范数误差(L2-norm error)：

(29)

图4 对压力驱动的稳定管道流使用不同的边界处理方法，E2随q变化情况Fig.4 E2 as a function of q using different boundary treatments for steady state pressure-driven channel flow

3.2 验证边界条件的质量守恒

通常，在LBM模拟中，由于使用插值边界条件，系统的质量难以做到完全守恒。在模拟的过程中，每个时步都存在质量泄漏的问题。在许多情况下，由于质量泄漏非常小并且最终能够在足够大的时间步长内接近零，因此人们往往容易忽略其对模拟结果的影响。但是，在某些情况下，这种质量泄漏会持续增加，从而严重影响模拟结果的准确性。

包含重力的Poiseuille流就是一个简单但非常有用的例子[26]。设流场的长和宽分别为100和50格子单位，重力为G=-ρgj，g=0.001，q分别取值0.2和0.8，流场左右使用周期边界条件[27]，计算结果如图5所示，利用FH格式、MLS格式、BFL格式、LL格式、YMS1格式、YMS2格式和TAO格式的曲线边界处理方法，系统的总质量会以恒定速率持续下降，而使用本文提出的HBI格式计算的总质量基本保持不变，实现了系统的质量守恒。

图5 使用不同的曲线边界处理方法，重力驱动下系统质量随时间变化情况Fig.5 System mass changes with time using different boundary treatments for steady gravity-driven flow

4 结语

本文提出了一种基于半程反弹的统一曲线边界处理新方法，并将该方法用于对2种不同的Poiseuille流进行数值模拟，以系统地测试其计算精度和数值稳定性，检验其是否存在质量泄漏问题。数值模拟结果表明，与常用的曲线边界处理方法相比，本文提出的边界处理方法具有以下优点：①计算公式统一，保证了边界处理的连续性；②增强了数值计算的稳定性并提高了计算精度；③应用半程反弹原理，在q取值0.5时，能够恢复半程反弹格式；④满足曲线边界上的质量守恒。本文提出的边界处理方法适用于无滑移边界，接下来进一步研究将其推广到运动曲线边界中。