带阻尼项的3D Navier-Stokes方程拉回吸引子的上半连续性

曹伯芳，姜金平，曹兰兰

(延安大学 数学与计算机科学学院，陕西 延安 716000)

0 引言

设Ω是R3中带有光滑边界∂Ω的有界区域，我们考虑以下带阻尼项的三维Navier-Stokes方程：

(1)

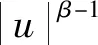
阻尼在自然界中普遍存在，它来自于流体的运动阻力，描述各种物理现象，比如多孔介质流，阻力或摩擦效应以及一些耗散现象[1-2]。从物理学角度来看，耗散对于非线性引起的构形中能量的聚积起着重要的扩散作用，影响着相应的非线性方程解的长时间动力学行为。因此，许多数学家和物理学家都开始关注具有耗散项的非线性方程, 关于这方面的研究已有很多(如文献[3-5])。

当α=0，问题(1)就为经典的3D Navier-Stokes方程，近几十年来关于3D Navier-Stokes方程已有大量的研究(见[6-12])。

关于方程(1)解的适定性问题，Cai[13]首次利用Galerkin逼近的方法讨论了3D Navier-Stokes方程的柯西问题，在β≥1时和β≥7/2分别存在弱解和强解，进一步验证7/2≤β≤5强解是唯一的。

随后在文献[14]中，Zhang等证明了问题(1)在β>3时强解是全局存在的，在3<β≤5时强解是唯一的。

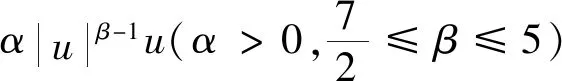
本文我们考虑利用文献[19]和[20]中的方法证明问题(1)的拉回吸引子的上半连续性。主要困难在于利用弱连续和分解的方法证明全局吸引子的存在性以及关于拉回吸引子在扰动意义下的上半连续性。

1 预备知识

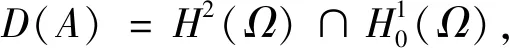
Hilbert空间，

其中α∈R,定义在Hα中的内积和范数为

分别定义双线性和三线性算子如下

B(u,v):=P((u·▽)v),

为了得到后面的定理，我们给出一些重要的不等式，三线性算子满足以下不等式(参见文献[21])。

b(u,v,v)=0,b(u,v,w)=-b(u,w,v),∀u,v,w∈V,

(2)

Ladyzhenskaya不等式：对于任意的u∈V,有

定义1[22]如果对任意开集V⊂X，满足G(λ0)⊂V，存在λ0的邻域U(λ0)，使得G(λ)⊂V,∀λ∈U(λ0)，则称G在λ0∈A处是上半连续的。

设S(t):X→X,t∈R+是一个C0半群，研究对任意的小参数ε∈(0,ε0]的非自治扰动系统拉回吸引子的连续性，即对∀t∈R,τ∈R以及x∈X，有

对X中的任意有界集是一致成立的。

定理1[19-20]当(H1)成立，对∀ε∈(0,ε0],存在拉回吸引子ɛ={Aɛ(t)}t∈R,且存在紧集K⊂X,有

下面我们证明(H2)。

引理1 假设集族={D(t)}t∈R关于过程U(·，·)是拉回吸收的，且对任意一个ε∈(0,ε0],ε={Kε(t)}t∈R是空间中的一个紧集族。假设Uε(·,·)=U1,ε(·,·)+U2,ε(·,·):R×R×X→X，使得

(i)对任意的t∈R和ε∈(0,ε0]，

‖U1,ε(t,t-τ)xt-τ‖≤Φ(t,τ),∀xt-τ∈B(t-τ),τ>0,

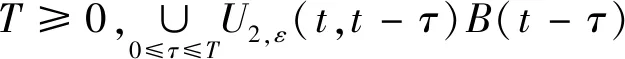
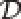
并且存在一个紧集K⊂X满足

成立。

则对∀ε∈(0,ε0]，ε={Aε(t)}t∈R是系统上的拉回吸引子并且(H2)成立。

证明参见文献[23]。

如果u∈L∞(τ,T,;H)∩L2(τ,T;V)∩Lβ+1(τ,T;Lβ+1(Ω))满足

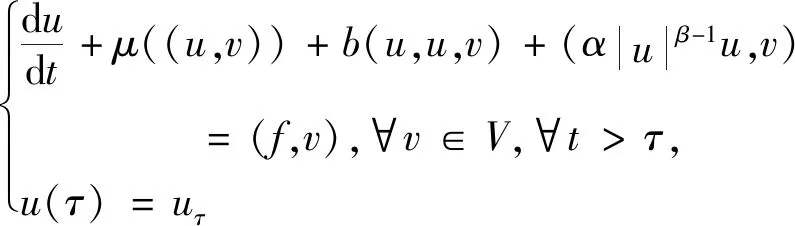
那么我们说u是方程(1)在[τ,T]上的一个弱解。

上述方程等价于以下方程

u∈L∞(τ,T;V)∩L2(τ,T;H2(Ω))∩L∞(τ,T;Lβ+1(Ω))

而且，解连续依赖于初值。当f(x,t)=0，即自治动力系统，上述结果也成立。

2 全局吸引子的存在性

本部分我们考虑在自治情形下方程(1)的抽象形式如下：

(3)

由于嵌入i:V→V′是稠密的，因此，对于任意的f∈V′， 我们可以找到一个依赖于f和ε的函数fε∈V使得

‖f-fε‖V′≤ε,

(4)

现在我们考虑分解u(t)=v(t)+w(t)，其中v(t)和w(t)分别满足以下方程

(5)

和

精细化的国别研究旨在把服务“一带一路”倡议的大目标转化为可实际落实的小目标。国别研究可以研究一个国家，也可以研究由几个语言文化相似国家组成的文化区域，以语言为切入点，进而研究该国或该地区的宗教信仰、文化习俗、禁忌习惯等多人文环境知识。同时，国别研究不应仅局限于了解有关国家的文化通识知识，还可以结合学生所学专业研究该专业在目标国家的发展现状、营商环境和法律制度等更具专业导向的国别知识。

(6)

由定理2，方程(3)的解是存在且唯一的，进一步，解连续依赖于初值。为了方便，我们记方程(5)和(6)的解分别为{Sv(t)}t≥0和{Sw(t)}t≥0， 因此，对于任意的u0∈V，有

u(t)=S(t)u0=v(t)+w(t)=Sv(t)u0+Sw(t)u0

引理2 设外力f∈V′，初值uτ∈V,则半群在V中存在有界吸收集B0，其中

B0={u∈V:‖u‖V≤ρ}

是V中的一个有界集合。

证明方程(3)两边与u做内积，在Ω上积分得

由Poincare不等式‖▽u‖2≥λ‖u‖2，

所以

利用Gronwall不等式，得

定理3 对任意的外力f∈V′，带有初边值问题的(3)和(4)生成的半群{S(t)},t≥0在V上是渐近紧的。

证明利用半群的分解定理，主要通过以下引理。

引理3 ∀δ>0,存在常数ε=ε(δ,f)，使得方程(5)满足

其中Q(·)是(0,+∞]上的非负增函数。

证明方程(5)中的第一式两边分别乘以v(t)， 在区域Ω上积分可得

根据Poincare不等式‖▽u‖2≥λ‖u‖2，

应用Gronwall不等式得

因此，我们选取合适的ε2≤λ2μ2δ，引理3得证。

证明对(6)中的第一式两边关于Aσw(t)做内积，积分得

(7)

(8)

(9)

根据文献[15]中的性质7，我们可以得到

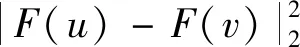
其中w=u-v，因此

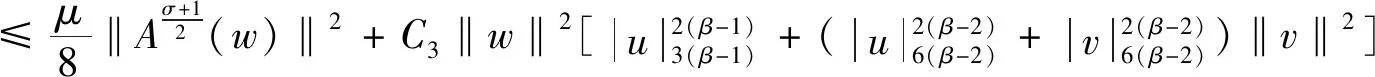
对(7)式结合(8)-(10)，可以得出

其中C4=C4(μ,‖fε‖2,‖u0‖2)，故

因此，引理4得证。

根据文献[26]中的引理3.2.6和定理3.4.6，引理3.2和引理3.3以及紧嵌入，我们有

引理5 对任意的外力f∈V′，带有初边值问题的(3)和(4)生成的半群{s(t)},t≥0在V上是渐近紧的。

因此，由文献[27-30]，引理2和引理5，可以得到以下定理：

定理4 对任意的f∈V′和初值u0∈V，问题(3)整体解所生成的半群{S(t)},t≥τ∈R存在一个不变的紧的吸收V中所有有界集合的全局吸引子。

3 非自治动力系统中带阻尼项的3D Navier-Stokes方程拉回吸引子的上半连续性

本部分我们将通过定理1和引理1证明方程(1)拉回吸引子的上半连续性。

考虑非自治动力系统的初边值问题

(11)

(12)

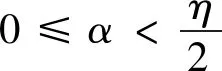
定理5 若(12)式成立，初值uτ∈V,则当ε>0时 ，非自治系统(11)的拉回吸引子ε={Aε(t)}t∈R和该系统当ε=0时的全局吸引子，对于任意的t∈R满足

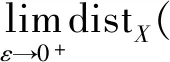
引理6 (1)假设uτ∈V，当扰动项中ε=0时，系统(11)变为自治动力系统，所生成的半群记为{S(t)},t∈R在空间V中存在全局吸引子。

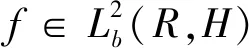
系统(11)的初始条件uτ∈V，现将方程的解分解为uε(t)=Uε(t,τ)uτ，

uε(t)=Uε(t,τ)uτ=U1,ε(t,τ)uτ+U2,ε(t,τ)uτ,

其中

U1,ε(t,τ)uτ=v(t)

U2,ε(t,τ)uτ=w(t)

分别满足

(13)

和

(14)

引理7 若(12)式成立，对于任意的有界集B∈V和t∈R,存在时刻T(B,t)>0,使得对于任意的τ≥T(B,t)和任意的ut-τ∈B,

证明方程(11)与uε做内积，因为三线性〈B(uε,uε),uε〉=0，经计算得

于是，

这里λ是算子A的第一特征值，则

因此

(15)

从(15)式可以推出

(16)

对式子(16)从t-τ到t积分，得

‖f(s)‖2ds

记半径r2=e-τη‖uε(t-τ)‖2。

(17)

如果我们令

Bε={uε∈V|‖uε‖V≤2Rε(t)}

(18)

则能得到Bε={Bε(t)}t∈R在V中是拉回吸收的，进一步有

引理8 设Rε(t)和Bε(t)定义如上(17)和(18)，对于任意的t∈R，问题(13)的解v(t)=U1,ε(t,t-τ)u(t-τ)满足

证明方程(13)式两边同乘以v(t)，分部积分得

对上式使用Poincare不等式得

设η1=2η>0，则

(19)

对(19)式从t-τ到t积分得

因此引理8得证。

证明将(14)式与w(t)在空间V中做内积，得

=〈B(w,w)-B(w,u)-B(u,w),w〉+ε〈f(x,t),w〉

(20)

利用三线性算子的性质〈B(w,w),w〉=0,〈B(u,w),w〉=0以及所满足的不等式(2)式，再结合Young不等式，可得，

〈(B(w,w)-B(w,u)-B(u,w)),w〉

≤C‖w‖2‖v‖2+μ‖▽w‖2≤Ce-η1τRε(t-τ)‖w‖2+μ‖▽w‖2

(21)

以及

(22)

结合(20)-(22)式，可以得出

对任意的t>τ，从t-τ到t积分可得

引理10 对∀t∈R和∀τ>0，问题(11)的解在空间V中，当ε→0+时，uε(t)=Uε(t,t-τ)u0收敛到u(t)=S(τ)u0，即

其中B是空间V中的有界子集。

证明令

yε(t)=uε(t)-u(t),

于是yε(t)满足

(23)

yε|∂Ω=0,

yε|t = τ= (uε)τ-uτ

方程(23)式两边同乘以yε(t)并积分，可得

=-〈B(u,u)-B(uε,uε),yε〉+〈εf,yε〉

≤|〈B(uε,uε)-B(u,u),yε〉|+〈εf,yε〉

≤‖B(uε,uε)-B(u,u)‖V‖yε‖V+

根据Poincare不等式‖▽yε‖2≥λ‖yε‖2，得

(24)

利用引理(7)-引理(9)，以及解的存在性可以知道

uε,u∈C([τ,+∞);H)∩L2(τ,T;V)∩L∞(τ,T;D(A)∩H)

即引理10得证

定理5的证明可结合引理7-引理10，以及引理1得证。