发动机特性数字化处理与数学建模

管湘源，储江伟，高伟健，赵小婷

(东北林业大学 交通学院，哈尔滨 150040)

0 引言

发动机是车辆的动力系统，是一个复杂的非线性、时变性及滞后系统[1]，使用真实发动机来设计控制器是一项费时费力的任务。因此，许多研究人员通过建立发动机数学模型来设计、测试和优化其控制器。汽车行业已经转向基于模型的校准来寻求解决方案[2]。当前主流发动机建模方法有两种：一种是解析法，即依据发动机的机理和相应参数关系而建立仿真数学模型；第二种是实验法，即通过发动机台架试验数据建立仿真模型[3-5]。

通过解析法建立数学模型，通常需要根据数据拟合(一般为曲面拟合法、多元插值法和综合法)来确定相关系数(即曲线或曲面的待定系数)，进而得到最终的数学拟合公式。利用Matlab拟合工具箱进行数据拟合，具有求解便捷和精度较高等特点，因而在机械、物理、电力、水利、医药和能源等多种学科领域均有广泛应用。在机械领域应用方面，郑啸洲等[6]通过Matlab拟合工具箱对某型发动机试验数据进行拟合处理，建立发动机的数学模型。在物理领域应用方面，陈文芳等[7]和魏奶萍[8]通过Matlab曲线拟合工具箱处理PN结的伏安特性数据,拟合得到相应的PN结伏安特性函数表达式；郭悦韶[9]通过Matlab曲线拟合工具箱处理霍尔效应实验测量数据，拟合得到磁场分布曲线；范隽宏等[10]通过Matlab曲线拟合工具箱对软磁材料的单位损耗数据的曲线拟合分析，得出用于变压器电磁计算的拟合方程；岳鹏等[11]以测量玻璃热膨胀系数和折射率温度系数实验、太阳能电池基本特性测量实验为例，通过Matlab曲线拟合工具箱处理物理实验数据，进行拟合实验曲线。在电力领域应用方面，李太兴等[12-13]通过Matlab曲线拟合工具箱进行火电厂运行的机组负荷优化分配；高艳平等[14]通过Matlab曲线拟合工具箱分析某发电厂的地基沉降实测资料，并拟合出多种不同的地基沉降预测模型。在水利领域应用方面，王杰等[15]通过Matlab曲线拟合工具箱求解分析抽水试验资料，并确定承压含水层的导水系数和导压系数。在医药领域应用方面，曹俊涵等[16]通过Matlab曲线拟合工具箱处理药物溶出数据，并计算药物溶出度Weibull分布参数。在能源领域应用方面，高鹏[17]通过Matlab曲线拟合工具箱对浮选尾矿灰分数据与图像灰度数据进行曲线拟合；何定武[18]通过Matlab曲线拟合工具箱分析风机特性曲线并计算风机实际工况下节电率。

在上述应用中，经过验证，由Matlab曲线拟合工具箱得到的拟合结果具有较高精度，因此本研究也选用Matlab曲线拟合工具箱作为曲线拟合工具，以某款发动机的外特性和万有特性曲线为例，通过Matlab曲线拟合工具箱cftool对提取的数据按照不同的拟合方法进行公式拟合，并根据拟合优度检验结果选择出最佳拟合公式，此公式即为最终确定的外特性曲线的数学模型。

1 发动机数值建模原理

以发动机台架试验数据的离散点或万有特性图数字化提取的坐标点数据作为样点，选择一种合适的函数逼近方式，将它重构成确定的数学模型，这是建模的关键。

发动机数学建模的原理是基于函数逼近，即函数的近似表示问题。函数逼近的方法多种多样，具体分类如图1所示。

图1 函数逼近方法分类Fig.1 Function approximation method classification

由图1可知，函数逼近的常规方法为拟合法、插值法和综合法。

1.1 曲面(线)拟合法

曲面(线)拟合法是选定近似函数H(x)后，不要求H(x)通过已知样本点，只要求在某种意义下H(x)在这些样点的总偏值最小。采用多元线性回归方法进行曲面拟合，构造发动机稳态输出转矩、油门开度以及发动机转速的关系。发动机的负荷特性数学模型构建为[19]：

(1)

式中：Me为发动机输出转矩，Nm；α为发动机的油门开度，%；ne为发动机的转速，r/min；B为系数矩阵。

通过最小二乘原理来确定系数矩阵B。建立的回归方程为[20]：

(2)

式中：b,e为系数矩阵B的余数。

写成矩阵形式如下：

Z=G·B+E。

(3)

G的列数k与多项式阶数s的关系为：k=(s+1)(s+2)/2。其拟合值和测量值的逼近程度可以用拟合度来评价。

1.2 多元插值法

插值法是给出函数f(x)的一些样点值，选定某些便于计算的函数，要求函数通过已知样点，由此确定函数H(x)为f(x)近似值。

采用多元插值法，构造发动机稳态输出转矩、油门开度以及发动机转速的关系。发动机的负荷特性数学模型构建为:

Me(t)=f(ne(t),αe(t))。

(4)

式中：Me(t)为发动机输出转矩，Nm；αe为发动机的油门开度，%；ne为发动机的转速，rad/s。

要计算的点ne、αe落在4个网格点中间，即

(5)

定义：

(6)

则：

(7)

其中，cij是插值系数，插值问题的核心就是求出插值系数，插值算法不同所求出的插值系数各异。

Matlab中的曲线拟合等相应的工具箱或cubic、linear、neast、spline、interpn、interpft、ndgrid等函数可以用来实现插值的功能。下面对比分析几种常用的插值方法的特点及用途，如图2所示。

图2 几种常用的插值方法Fig. 2 Several interpolation methods

1.3 综合法

综合法是融合多项式拟合与一元函数插值的方法。它首先根据最小二乘原理，拟合得到每个转速下的T=f(α)；然后对于某一工况点A，根据转速判断最临近于工况点A的3条负载特性曲线，再用该曲线的多项式计算出来A点α对应的转矩Ti-1、Ti、Ti+1的值，最后用插值法求得T(α)[23]。

2 万有特性图数字化方法

传统数据提取方法是进行手工测量和估算，此种方法不但误差大，而且效率低。因此，有必要采取数字化方法提取万有特性曲线图的数据。选用图像数字化软件Get Data作为数据提取的工具，其提取数据流程如图3所示。

提取数据前，需对图像进行预处理，包括图像的放大、截取和摆正等清晰化过程。良好的预处理可以在一定范围内降低视觉误差和分辨率误差，从而使获得的数据更为精确。

文中选取某款汽油机，根据厂方提供的万有特性曲线(图4)和外特性曲线(图5)的图像数据，对图上的数据进行采集，提取为数据表形式，为后期建立数学模型奠定基础。

图3 Get Data提取数据流程图Fig.3 Get Data extraction data flow chart

将万有特性曲线(图4)和外特性曲线(图5)分别导入Get Data软件，经过设置曲线颜色、设置背景色、设置基准点与取值范围的几个前期过程后，选择曲线相应坐标点，进行对应数据的提取。万有特性曲线的数据提取，如图6所示。外特性曲线的数据提取，如图7所示。

图4 发动机万有特性曲线Fig.4 Engine universal characteristic curve

图5 发动机外特性曲线Fig.5 Engine external characteristic curve

图6 万有特性图坐标点数据提取Fig. 6 Universal feature map coordinate point data extraction

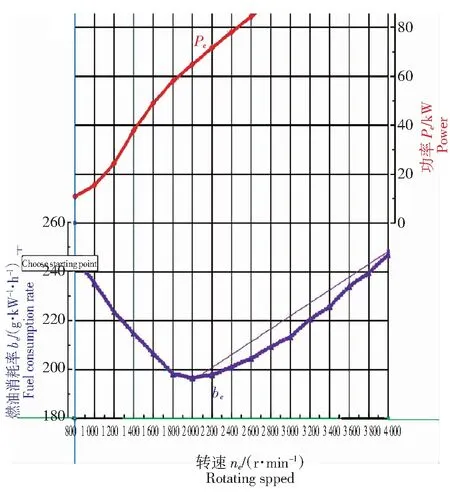
图7 外特性图坐标点数据提取Fig.7 External characteristic map coordinate point data extraction

提取的所有坐标点的数据将显示在工作区间内，可将数据导出为表格形式，见表1。

表1 导出的部分数据

除此之外，也可以选用Origin Pro软件进行数据提取，其提取具体流程如图8所示。

3 发动机数学建模

3.1 外特性模型

外特性建模采用曲线拟合的方法。首先初步确定外特性曲线的函数表达式(即确定近似函数)，进而选择相应的拟合方式得到最优拟合系数，最终得到完整的外特性数学模型。

图8 Origin Pro提取数据流程图Fig.8 Origin Pro extraction data flow

3.1.1 函数形式确定

发动机外特性是研究汽车动力性的基础,它是在发动机节气门全开的情况下,发动机转矩Me(或功率Pe)、燃油消耗率be与发动机曲轴转速ne之间的关系,可以看作是发动机转速的一元函数[24]。

分别用x表示ne，y表示Me、Pe或be，n为拟合多项式的最高阶数。

假定其函数形式为：

y=p1+p2x+p3x2+…+pnxn。

(8)

3.1.2 拟合方式选择

本文以Matlab的曲线拟合工具箱cftool作为拟合工具。cftool中包含的拟合方法有：Exponential指数拟合、Fourier傅里叶拟合、Gaussian高斯法、Interpolant内插法、Polynomial多项式(1～9阶)、Rational有理拟合、Power幂指数拟合、Smoothing spline平滑样条拟合、Sum of Sin Functions正弦曲线拟合、Weibull两个参数的Weibull分布，并支持Custom Equations用户自定义。

本文选用多项式拟合方法，并分析拟合效果，在后续拟合优度检验一节中给出详细说明。

发动机外特性模型按以下流程进行拟合：将发动机转矩Me(或功率Pe)、燃油消耗率be和发动机转速ne的数据分别导入到cftool工具箱中，发动机转速ne设置为x，燃油消耗率be、发动机功率Pe和发动机转矩Me分别依次设置为y。随后设置权重，默认值为1。完成初始数据设定后，选择拟合方法。拟合运算执行后，其结果在Results中显示，如图9所示。

图9 拟合结果Fig.9 The results of fitting

在拟合过程中，选择“Center and scale”(标准化)，可减少出现病态矩阵的情况。采用拟合算法时应尽量选择合适的最高幂次[25]，但并非次数越高越好。因为当次数过高，容易出现龙格(Runge)现象，导致在试验点以外的数据上偏差可能很大。

3.1.3 数学模型确定

通过多项式拟合得到外特性的最优拟合系数，最终得到外特性数学模型，见表2。

表2 外特性曲线的最佳拟合公式Tab.2 Best fit formula of external characteristic curve

3.2 万有特性模型(油耗模型)

发动机的燃油消耗率be是发动机转速和有效转矩(ne,Me)的函数，设发动机万有特性的函数类型为多项式[26-29]，其回归模型的矩阵形式为[30-31]：

be=[1,ne,Me,ne2,neMe,Me2,…,neMel-1,Mel]×

(9)

式中：a0、a2、…、ak-1为模型中的待定系数；e0、e2、…、ek-1为随机误差；l为多项式的最高幂次；k为多项式的项数，k=(l+1)(l+2)/2[29-30]。

发动机万有特性曲线的数学模型在cftool工具箱中的建立流程类似于外特性曲线的建立流程，在此不做赘述。

4 拟合优度检验

为评价拟合的性能，需对拟合结果进行拟合优度检验。具体的检验方法为：

(1)查看图的拟合结果“Examine the Graphical Fit Results”。选择Axes Limits，放大x轴坐标，显示曲线的变化趋势，若拟合曲线的整体趋势与预期趋势一致，则表明拟合效果较好。

(2)检查数值结果“Evaluate the Numerical Fit Results”。拟合结果指标“Goodness of fit”中包含4个指标，分别为：SSE(the sum of squares due to error)误差平方和、R-square复相关系数、AdjustedR-square调整自由度的复相关系数、RMSE(Root mean squared error)均方根误差。

当SSE值和RMSE值越小，R-square值越接近于1时，说明拟合效果越好。

(3)若结果中显示“Fit computation did not converge”或“Equation is badly conditioned”，则说明拟合效果较差。可通过改变最高阶次数、调整拟合算法或选择“居中和缩放”来加以改善拟合效果[10]。

(4) 对于多项式拟合，多项式阶数越高，若拟合系数的置信区间接近0，说明可能为过度拟合。

本研究以外特性曲线中燃油消耗率be与发动机转速ne的拟合为例，根据之前所确定的外特性函数形式，选择多项式拟合方法，分别作1～9阶的多项式拟合，每阶分别选择OFF(常规最小二乘法)、LAR(最小绝对残差法)、Bisquare(加权最小二乘法，默认算法)3种回归模式，进行拟合效果对比，如图10—图12所示。图10—图12中分别标出各拟合结果指标的极大值和极小值。当SSE和RMSE值越小，R-square值越接近于1时，说明拟合效果越好。

图10显示RMSE在9阶多项式拟合的OFF模式(常规最小二乘法)下取得极小值，图11显示SSE在9阶多项式拟合的OFF模式(常规最小二乘法)下取得极小值，图12显示在9阶多项式拟合的OFF模式(常规最小二乘法)下R-square和AdjustedR-square值均趋近与1。

综上所述，在9阶多项式拟合的OFF模式(常规最小二乘法)时，拟合效果最好。由此，得到最终拟合公式为：

be=1.128×ne9+0.7566×ne8-7.806×ne7-

4.719×ne6+20.37×ne5+7.679×ne4-

27.07×ne3+15.97×ne2+17.85×ne+

200.1。

(10)

图10 1～9阶多项式拟合RMSE值Fig.10 1—9 order polynomial fitting RMSE value

.

将最佳拟合(9阶多项式拟合的OFF模式)和最差拟合(此处选取1阶多项式拟合的LAR)的拟合效果图作对比，如图13所示，两者的残差图作对比，如图14所示。

图13 最佳拟合和最差拟合的拟合效果对比Fig.13 Comparison of fitting effects in the best & worst fit

图14 最佳拟合和最差拟合的残差图对比Fig. 14 Comparison of residual plots for best & worst fit

由图13和图14反映出，若拟合曲线与拟合多项式的基底高度相关(整体趋势一致)，且残差绝对值较小，则表明拟合效果较好。

5 结论

利用Matlab曲线拟合工具箱cftool进行曲线拟合更为简单便捷。这种方式特别适用于自编程序或联合仿真。

初步拟定的函数关系式对后续拟合方法的选择至关重要。另外，在拟合过程中，根据初步拟定的函数关系式，可以多加尝试不同的拟合方法，对比其SSE(误差平方和)、R-square(复相关系数)、Adjusted R-square(调整自由度的复相关系数)、RMSE(均方根误差)，据此选择最佳的拟合方法，得到更精确的拟合公式，提高后续仿真模拟的精度，增强健壮性和可靠性。