基于相位校正的EPS系统控制策略仿真研究
2020-01-15李志鹏郝宇张超孟旭王博男
李志鹏,郝宇,张超,孟旭,王博男
(东北林业大学 交通学院,哈尔滨 150040)
0 引言
随着汽车行业的高速发展,对汽车内部各系统的研究变得尤为重要,其中汽车的转向系统是车辆安全行驶的重要组成部分,当前汽车的转向系统大体上可分为3类:机械转向技术、液压转向技术和电动助力转向技术。
电动助力转向系统相比于传统的液压动力转向系统具有结构紧凑、质量轻、易于维修保养的优势,并且安全、舒适和节能,更适合现代汽车的发展方向[1-3]。电动助力转向系统的研究主要是对控制系统的研究,传统的控制方式会存在一定迟滞和不稳定性,本文设计相位校正装置来改善系统的稳定性并提高系统的响应。
1 EPS系统动力学模型
1.1 EPS系统的工作原理和结构
EPS系统通过收集汽车转向时车速的信号和转向盘转矩的信号,依靠电子控制单元(ECU)来处理这些数字信号,并以此来调节助力电机的扭矩,降低转弯时驾驶员操作的难度。
图1是典型的电动助力转向系统的结构图。该电动助力转向系统主要由4部分组成:电子控制单元(ECU)、机械转向装置、助力电机和助力机构。
1.2 EPS系统的动力学方程
EPS系统的简化动力学模型如图2所示,可以将整个EPS系统简化成4部分,分别为方向盘、转向轴、齿条齿轮机构和电机[4-6]。

图1 EPS系统结构图Fig.1 EPS system structure
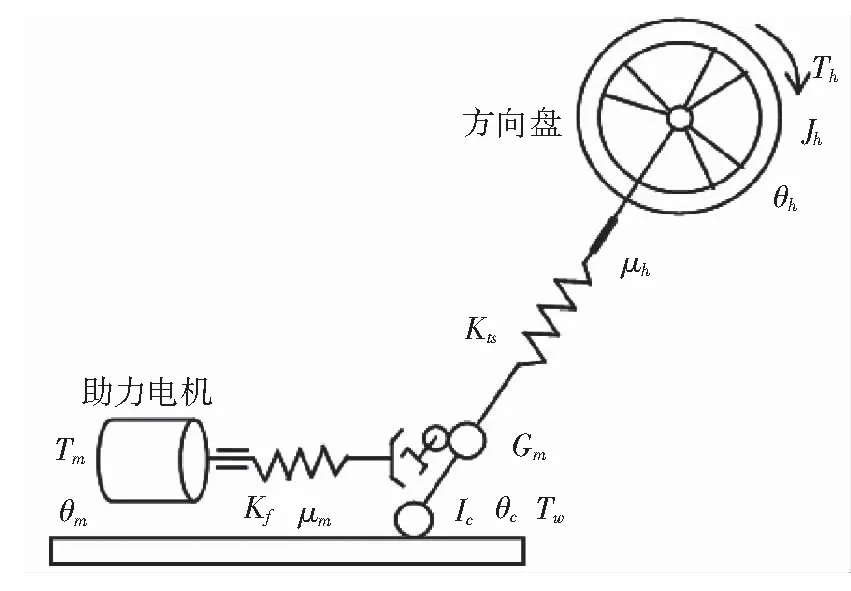
图2 EPS系统动力学模型Fig.2 EPS system dynamics model
1.2.1 机械转向系动力学方程
根据牛顿运动学定律,通过对方向盘、转向轴和齿条齿轮机构的动态分析,得到以下公式。
转向盘:
(1)
式中:Jh为转向盘的转动惯量,kg·m2;μh为转向盘的阻尼系数,θh为驾驶员对转向盘的输入转角,(°);Th为驾驶员对转向盘的输入扭矩,N·m;Tts为扭矩传感器的传感扭矩,N·m。
Tts=Kts(θh-θc) 。
(2)
式中:Kts为转向轴的刚度;θc为转向轴的转角,(°)。
联立公式(1)与公式(2)得到方程:
(3)
转向轴:
(4)
式中:Jc为转向轴的转动惯量,kg·m2;μc为转向轴的阻尼系数;Ta为电机工作时产生的助力转矩;Tw为电机工作时作用在转向轴上的阻力矩,N·m。
联立公式(2)与公式(4)得到方程:
(5)
齿轮齿条机构:
(6)
式中:mγ为等效齿轮齿条机构的等效质量,kg;μγ为齿条的阻尼系数;xγ为齿条的平移位移,m;γp为小齿轮的半径;Fγ为轮胎与路面间的作用力,N;Fσ为汽车前轮作用在齿条上阻力,N。
1.2.2 助力电机动力学方程
运行期间电机产生的辅助扭矩的微分方程:
(7)
式中:Tm为电机工作产生的电磁转矩,N·m;Jm是电机的转动惯量,kg·m2;μm为电机的阻尼系数,θm为电机工作时的转角,(°);Gm为减速器的减速比。
电机工作产生的电磁转矩与其产生的电枢电流成正比,比例系数为Kf,由此可以得出电动机的机械特性方程:
Tm=KfI。
(8)
式中:Kf为转向轴的刚度;I为电机工作产生的电流,A。
根据基尔霍夫定律,通过对电动机电路的分析,可以建立电机的电气回路微分方程:
(9)
式中:U为电机工作时产生的电压,V;R为电机工作时产生电枢电阻,Ω;L为电机工作时产生的电感,H;Kg为电磁力矩常数。
在电机工作过程中,电机的转角与转向轴的转角成正比,比例系数为Gm。
θm=Gmθc。
(10)
联立公式(7)、公式(8)、公式(10)可以得出电机助力转矩与电枢电流的关系式:
2 车辆动力学模型
将车辆动力学模型简化成二自由度1/4车辆模型[7-9],如图3所示。

图3 二自由度车辆模型简图Fig.3 Schematic diagram of a two-degree-of-freedom vehicle model
其中,x轴正方向是汽车前进方向,y轴正方向是指向驾驶员的左侧,z轴正方向是指向驾驶员的上方。
根据运动学规律,经受力分析可知,沿y轴方向的合力方程:
∑FY=Fyr+Fyfcosδ。
(11)
绕z轴的合力矩方程:
∑MZ=lrFyfcosδ-lfFyr。
(12)
在实际工作中,δ的值较小,可以将上述两个方程写成如下:
(13)
其中:
(14)
(15)
联立公式(11)、公式(12)、公式(13)、公式(14)和公式(15)并经整理得:

式中:Fyr、Fyf是前后轮胎的侧偏力,N;lr、lf分别是前后轴中心到质心的距离,m;k1、k2是前后轴的等效刚度;m是汽车的等效质量,kg;vx是车辆速度在x轴上的分量,m/s;δ是前轮转角,(°);β是质心侧偏角,(°);IZ是汽车的等效转动惯量;ωr是汽车橫摆角速度,rad/s;α1、α2是前后轴侧偏角,(°)。
3 模糊控制策略
EPS系统是通过对助力电机电流的控制,并以此来调节电机的输出电压,进而使驾驶员在转向时降低对车辆的操控难度,本文设计模糊PID控制器对EPS系统中的助力电机的电流进行闭环控制。
模糊PID控制系统是将PID控制系统和模糊控制系统相结合而产生的智能PID控制系统,其原理是将误差和误差变化率模糊化,并建立模糊规则,在进行模糊推理后以便能够实时调节比例、微分和积分3个系数,从而来改善系统的性能[10-13]。
模糊PID控制的公式为:
式中:Im是目标电流;I是实际检测电流;kp、ki、kd分别是比例、微分、积分系数。
电流误差e,电流误差变化率ec,kp、ki、kd的论域使用模糊子集来进行定义,表示成NB、NM、NS、ZO、PS、PM、PB,其中可以将NB记为-3,NM记为-2,NS记为-1,ZO记为0,PS记为1,PM记为2,PB记为3,电流和电流变化的论域可以表示为e、ec、kp、ki、kd=[-3,-2,-1,0,1,2,3],然后确定各个变量的隶属度函数,本文采用梯形隶属度函数来描述e、ec、kp、ki、kd的模糊性,制定模糊规则,建立模糊规则表,见表1—表3。分别是比例系数kp、微分系数ki和积分系数kd的模糊控制规则表[14-19]。

表1 kp模糊规则表Tab.1 kpfuzzy rule table

表2 ki模糊规则表

表3 kd模糊规则表
根据建立的模糊规则表,进行模糊推理,模糊推理后得到比例系数kp、微分系数ki、积分系数kd的模糊量,这些模糊量不能直接作为控制量,需要对模糊量进行反模糊化,从而得到清晰并且精确的控制量。本文使用面积平分法去除模糊化,面积平分法是将隶属度函数曲线与坐标轴围成的面积等分成两等份的平分线横坐标值,来表示模糊量,即得到比例、积分和微分3个系数的值,从而完成模糊PID控制器的设计。
4 EPS系统的相位校正
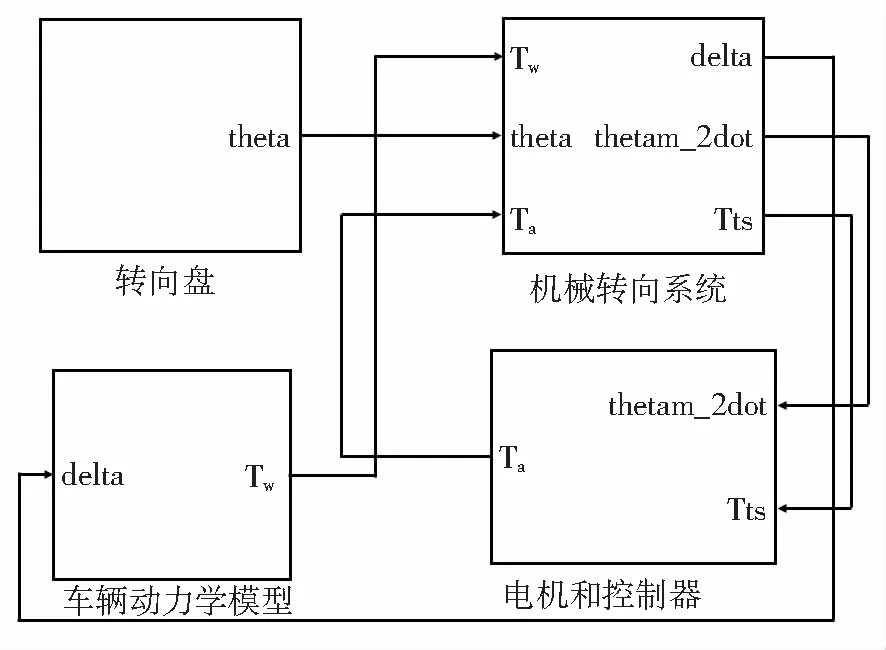
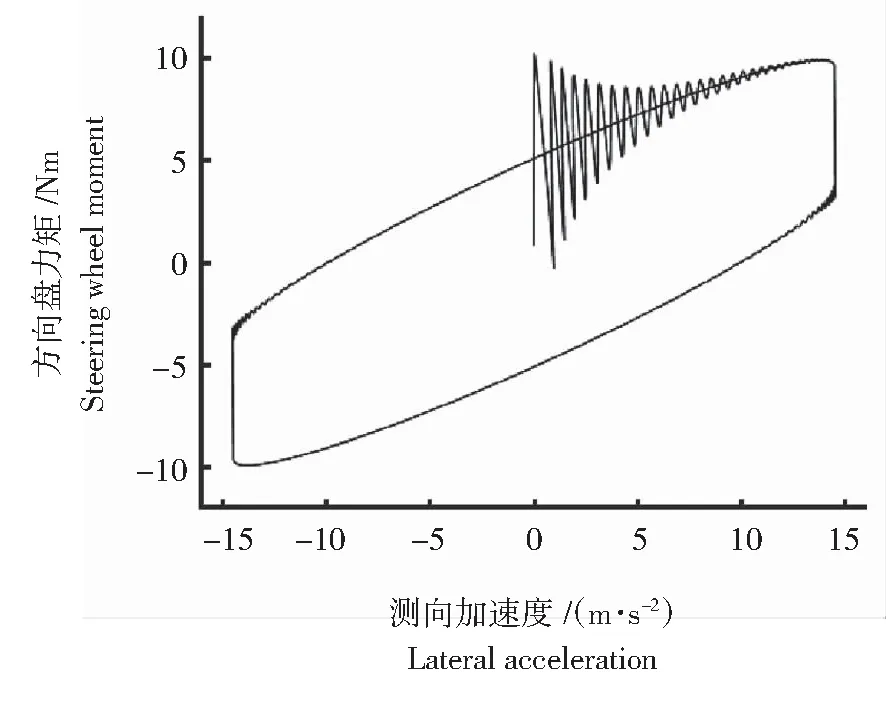
在EPS系统工作时,受系统噪声和来自路面的干扰,会使EPS系统的响应产生一定的迟滞,从而降低驾驶员对汽车的操纵手感。为增加汽车的操纵手感,提高EPS系统的响应,设计相位校正装置来补偿系统相位,校正环节的传递函数为G(s)=(Ts+1)/(aTs+1),其中(0 图4为进行相位校正前后的系统仿真对比Bode图,由图4可以看出,在校正前,虽然系统是闭环稳定的,但是频率wc=68.4 rad/s,相位角余量r=4.85°,频率与相位角余量的值太小,它会影响系统的响应和稳定性,导致系统工作有一定的延迟。而校正后的频率为wc=92.6 rad/s,相位角余量r=44.8°, 图4 波特图Fig.4 Bode diagram 大于 40°,因此该校正装置满足设计要求。校正后系统的频率和相位角余量大幅提升,提高了系统的响应和系统的鲁棒性能。 使用Matlab/Simulink软件来建立EPS系统和整车仿真模型,如图5所示。 图5 EPS系统仿真模型Fig.5 EPS system simulation model 在仿真过程中车速为30 km/h,方向盘采用正弦输入,观察方向盘转矩、方向盘转角和侧向加速度的时域响应特性,绘制出方向盘转角和方向盘转矩以及侧向加速度的关系曲线。 图6和图7是没有加入校正环节的仿真图,在起始阶段方向盘的转矩随着方向盘的转角和侧向加速度的增加,产生剧烈的波动,增加了驾驶员对汽车的操控难度。 图6 方向盘力矩随转角变化图Fig.6 Steering wheel torque with angle change diagram 图7 方向盘力矩随侧向加速度变化图Fig.7 Steering wheel torque as a function of lateral acceleration change diagram 图8和图9是加入校正环节后的仿真图,在起始阶段方向盘的转矩随着方向盘的转角和侧向加速度的增加,波动幅度较没有加入相位校正装置的明显减小,从而提高了驾驶员对汽车的操控。 图8 方向盘力矩随转角变化图Fig.8 Steering wheel torque with angle change diagram 图9 方向盘力矩随侧向加速度变化图Fig.9 Steering wheel torque as a function of lateral acceleration change diagram 本文使用Matlab/Simulink建立EPS系统模型和整车模型,并设计了相位校正的装置,进行仿真,结果显示通过对比两次仿真结果可知,如果控制器和助力电机只是单纯地将力矩传感器所测量的转矩进行放大而不加以任何校正,那么 EPS 系统会加剧转向操纵过程中初始阶段以及转动方向改变阶段的方向盘力矩波动,使系统变得不稳定。在 EPS 系统的控制器中加入相位校正装置以后可以发现,转矩波动被明显地改善了。
5 仿真及结果分析



6 结论
