基于图论模型的间接平差计算

胡波，李超，黄赟

(1.重庆市勘测院，重庆 400000； 2.重庆市智能感知大数据产业协同创新中心，重庆 400000)

1 引 言

控制网测量数据处理工作的一般化流程是先进行坐标概算，再进行平差计算。通过坐标概算可获得较为准确的近似坐标，为测量平差计算提供基础[1～4]。现有的坐标概算设计以单测站重复迭代处理为主，较少考虑测站间的关联性和顺序性。图论是一种对数据进行关联建模、分析及挖掘的有效方法，在电网、交通等相关领域获得了广泛应用[5～7]。本文根据测量数据观测的特点，给出了控制网有向图的建模方法，基于广度优先算法进行坐标概算，并利用Python脚本进行算法实现。

2 图论建模

2.1 基本理论

图G可以表示为一个二元组(V，E)的集合，其中V是图的顶点集合，E是图的边集合。常用v(E)表示G的顶点集，e(E)表示G的边集，e(u，v)为图中的一条边，w(u，v)为该边的权值。其中e考虑其方向性时，为有向图；无方向特性时，为无向图。根据顶点和边在现实世界中的不同映射，分别赋予不同权值，可实现对现实世界的动态网络模拟与分析。如设定道路网络的交叉口为图的顶点、道路为图的边，道路长度为边的权值，则可以将道路抽象为有向图，从而开展实时动态导航与历史路径回溯[8]，如图1所示。

2.2 控制网建模

测量控制网由控制点和观测值构成，参照图论的建模方法，将控制点定义为顶点，当控制点间存在观测值(如距离、角度、高差等)时构建连接边，边的权属性以观测值确定，考虑到实际控制网观测过程中存在对向观测，将控制网构建为有向图。一个完整的平面控制网图模型构建过程如图2所示，其中A，B为测站观测点，1～4号为其他测点，A站共观测了1，2，3，B点，构建A站的连接边，B站观测了A，1，2，3，4，构建B站的B连接，A，B站存在对向观测，构建双向连接边。

图1 路网图论建模

图2 控制网图论模型构建

2.3 图遍历算法

广度优先搜索算法是一种常用的图论遍历算法，选取图中的某个点作为初始节点，遍历该节点的所有邻接节点，判定目标节点是否在邻接节点中，若没有，再对邻接节点进行重复上述操作，直至发现目标节点为止。

深度优先搜索算法是另一种常用的图论遍历算法，同理选取图中的某个点作为初始节点，利用规则生成排序后的首层邻接节点，选取首个邻接节点进行判断是否为目标节点，不是则对该节点构建新的规则排序后的邻接点层，循环上述操作直至发现目标节点，当遍历至最底层都未发现目标节点时，则返回上一层邻接点对后续节点进行重复遍历搜索。

从上述两种常见的搜索算法可以看出，确定初始节点是关键环节。在控制网图模型中，也就是基于既有已知条件确定坐标概算的起算点，常见的起算点包括：①基于已知定向边的起算点，如图2中的A，B均为已知点时，可任选一点作为初始节点；②基于后方交会观测方法确定的起算点，将交会得到的测站点作为初始节点；③基于测站已知点的起算点，如水准网、GNSS控制网中的任一测站已知点可选为初始节点。

2.4 坐标概算

在构建控制网的图论模型，确定起算初始节点后，根据控制网网型的差异，分别采取不同的遍历算法进行坐标概算。如导线网采用深度优先搜索算法，确定导线起点到终点间的最短路径，按照最短路径上的节点顺序进行坐标推算；平面网采用广度优先搜索算法，以初始节点开始，分层进行坐标推算。以平面网为例，坐标概算的流程如图3所示：

图3 坐标概算流程

根据广度优先算法确定从初始节点开始进行的测点坐标概算的顺序，按层级构建邻接测点，当前测点存在测站观测记录时，进行当前测站的坐标概算，根据观测条件分别采用极坐标、三角高程、几何水准方法进行，利用概算得到成果循环进行下一测点的坐标概算。该算法一次遍历所有测点，得到的概算成果基于最短路径进行，可提高坐标概算成果的精度。进行单测站坐标概算时，如果测站和测点间的观测值缺失，可根据有向图采用对向观测值进行补齐，实现一次遍历概算。

3 程序设计

本文采用Python脚本语言实现控制网坐标概算及间接平差。Python是一种动态的、面向对象的脚本语言，具有一套标准库，同时可以利用第三组件库完成各种复杂计算任务，目前被广泛应用数据挖掘、机器学习、科学计算、深度学习等任务中。本文利用igraph图论分析库进行图模型的创建，利用numpy，pandas库进行矩阵运算实现最小二乘法间接平差。以清华三维为例，观测数据标准格式如图4所示，第一部分是起算数据，第二部分是观测数据。

图4 观测数据格式

程序实现的关键步骤包括：①图的构建；②坐标概算；③平差计算。

(1)图的构建

首先对观测数据文件进行读取，形成测站观测列表，测点列表，再根据测站列表构建有向图模型G(V，E)。

(2)坐标概算

根据算法流程设计，确定控制网坐标概算的起点，如平面控制网的起算条件是两个相邻已知点或一个已知点和初始方位角，再利用广度优先搜索算法进行遍历，该过程调用igraph库的bfsiter函数实现。坐标概算过程中某个测点不存在测距观测值时，可以利用对向观测值进行计算，基于图论模型可以实现对向观测数据的快速存取。

(3)平差计算

首先是根据测站观测记录建立观测方程，确定矩阵B，L，P，V，再根据观测矩阵进行迭代最小二乘间接平差计算。

4 算法验证

4.1 基本精度验证

以附和一级导线(如图5所示)为例，进行算法基本精度验证。该导线总长为 790 m，包括4个监测点，利用本文的程序进行坐标概算和迭代平差计算，以清华三维平差计算结果为真值，计算对比结果如表1所示。算例以IJ15X为起算点，从表1可知，附和导线端点PJ53的概算坐标差值最大，X方向达到 -8.6 mm，Y方向为 1 mm，与导线坐标概算的规律一致，经过迭代间接平差后，所有导线点坐标差值均小于1个mm，平差计算结果与清华三维精度相当。

图5 附和导线图

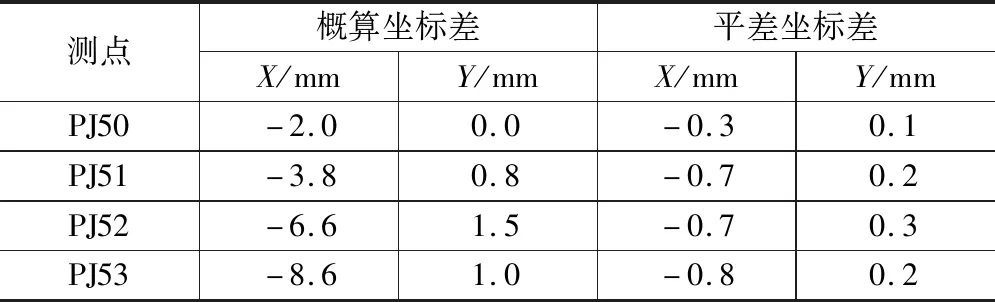
计算结果对比 表1

4.2 大型工程验证

以重庆市璧山片区大型一级导线控制网为例，进行算法的可靠性和稳定性验证。该项目在平面四等GPS控制点联测导线网，共布设一级平面导线点185个，总长度 72.3 km。清华三维平差结果为导线相邻点的相对点位中误差最大为 19.1 mm，最弱点点位中误差为 43.5 mm。本算法跟清华山维平差结果对比，平面差值的分布如图6所示，其中160个点平面差值小于10个mm，占比达到86.5%，保持了较好的一致性，点位的最大平面差值为 30.8 mm。部分点位平面差值较大，受到迭代过程中平差定权策略影响，这个也是本算法后期优化研究的方向。

图6 坐标差值密度分布

5 结 语

采用图论模型进行控制网的坐标概算，利用广度优先遍历算法可一次准确推导所有测点的近似坐标，并利用Python脚本进行平差算法实现，通过在具体工程中进行实践验证表明，该方法具有极好的稳定性和可靠性，可用于测量平差数据处理工作，Python实现的平差算法可进一步应用于海量测量数据挖掘与应用中，实现测量计算模型的服务化。