超远距离通信中的LDPC 译码实现

白建国，郝向新，郑 亮，代泽荟

（内蒙古电力（集团）有限责任公司鄂尔多斯电业局，鄂尔多斯 014399）

无人机远距离通信数据链是这些年发展日趋成熟的无线传输系统，它的主要功能主要是利用无人机飞行平台，将安装在机身的光电设备（如光电吊舱）所采集的连续图像实时，传输到地面监视点。目前采用的主要技术手段也非常丰富，比如Wi- Fi、微波、3G 或者4G 公网以及COFDM 技术等。本课题所采用的无人机远距离通信数据链技术方案需要在通信距离150km 的情况下，回传速率可以达到2Mb/s 以上，可以满足无人机超远距离通信应用的需要。因此，我们需要采用接近香农限的编码方式LDPC。

1 LDPC 简介

LDPC 码全称低密度奇偶校验码，是一种线性分组码，其通常由奇偶校验矩阵定义，该奇偶校验矩阵是一个稀疏矩阵，所以叫低密度奇偶校验码。码长较长的LDPC 码可以在极低的信噪比条件下实现无差错传输，具有逼近香农限的性能，如图1所示：

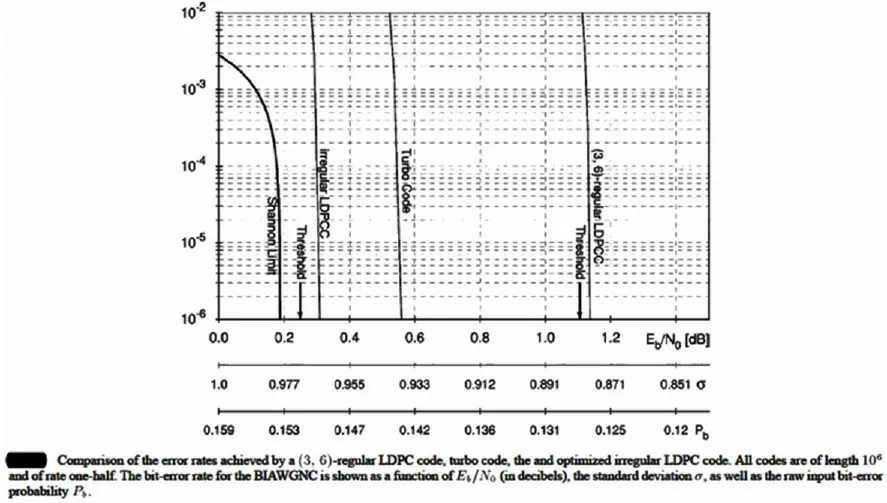
图1 LDPC码性能

LDPC 码主要优点：一是码长比较长的LDPC 码可以在极低的信噪比条件下实现无差错传输，具有逼近香农限的性能；二是LDPC 码通常用BP 算法译码，该译码算法复杂度和奇偶校验矩阵中非零元素成正比，奇偶校验矩阵中非零元素和码长成正比，从而对长码长LDPC 码可以实现线性时间复杂度译码，从而逼近香农限不仅存在，而且是可实现的；三是BP 译码算法具有内在并行性，可以用高度并行的结构实现，可以达到极高的译码吞吐量，吞吐量达到上Gb/s 的译码器已经出现。

LDPC 码的缺点：一是LDPC 码属于分组码，具有分组码的普遍缺点：改变码率和码长比较困难；二是为了实现线性时间复杂度编码，LDPC 码编码通常是用奇偶校验矩阵来完成的，这要求其奇偶校验矩阵具有特殊的结构，这个在设计LDPC 码的时候必须专门考虑；三是LDPC 码的译码算法具有较高复杂度，实现成本高；四是性能比较好的LDPC 码码长比较长，译码延迟大，比较适合宽带通信；五是LDPC 码在短码长时性能比较差。

LDPC 码可以分成正则（reg ular）和非正则（ir regular）两种：正则LDPC 码奇偶校验矩阵的每行的行重量都是相同的，每列的列重量也是相同的；而非正则LDPC 码的行列重量可以不相同，是符合一定的分布。对于相同码长和码率的LDPC 码，非正则LDPC 码性能要比正则LDPC 码好。正则LDPC 码性能取决于奇偶校验矩阵的girth，girth 越高性能越好；非正则LDPC 码的性能主要取决于奇偶校验矩阵列重量的次数分布，girth 也有一定的影响。

通常，通信系统中使用较多的是二元域LDPC。二元域LDPC 的奇偶校验矩阵H 是一个只有0元素和1元素的矩阵，其大小为，n 表示码长，m 表示校验位长度，信息比特长度k=n-m。下面叙述中的LDPC 都是指二元域LDPC。

如果定义LDPC 的H 矩阵中的1 元素的位置是随机，则该LDPC 码被称为随机的；如果定义LDPC 的H 矩阵中的1元素的位置是有一定结构的，则该LDPC 被称为结构化的。

2 结构化LDPC 简介

通常，结构化LDPC 码可以通过一个大小为（mb×z）×（nb×z）的矩阵H 来定义。它由大小为z×z 循环移位矩阵块或大小z×z 为0的矩阵组成，形式如下：

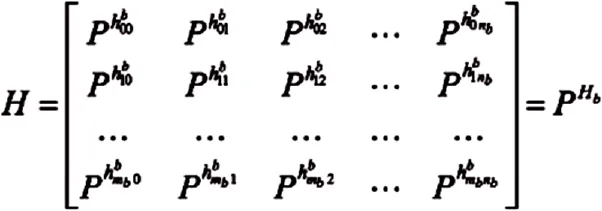
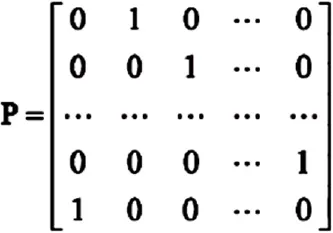
所以，H 矩阵的大小是M×N，其中N=nb×z，M=mb×z，z 是一个正整数。基础矩阵Hb 的大小为mb×nb，形式如下：

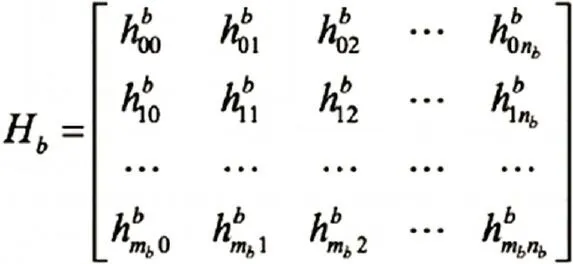
这种结构化LDPC 有几个概念：H 是Hb的扩展矩阵（expand matrix），Hb是H 的基础矩阵（base matrix），z 是扩展因子（expand factor）。

扩展基础矩阵的时候将Hb中的非负元素替换为z×z 大小的置换矩阵，并将其中的-1元素置换为z×z 大小为的零矩阵。

置换矩阵使用的是循环右移置换，所以在基础矩阵中元素0表示z×z 单位阵，元素1表示z×z 单位阵循环右移一列对应的矩阵，-1元素表示z×z 零矩阵。

这样的结构化LDPC，信息长度K 等于N-M，这里N 是码块比特长度，M 是校验比特长度。通过改变扩展因子z 的大小，一个基础矩阵可以支持不同的码长。

基础矩阵的修正准则定义如下：

式中，zmax是最大的扩展因子（the largest expand factor），这里等于512；z 是对应当前码长的扩展因子；[]表示向下取整。

3 算法描述

本项目中的LDPC 码是一种具有准循环结构的LDPC 码，这类码字具有编码结构简单的特点。QC－LDPC 码的校验阵可以通过一个模版矩阵扩展得到，模版矩阵Hb可以分成两部分Hb1和Hb2，其中Hb1对应系统位部分，Hb2对应校验位部分，这样：

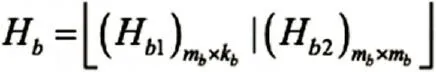
Hb2可以分成两部分Hb和H'b2，其中矢量Hb的列重量是奇数，H'b2具有双对角结构：

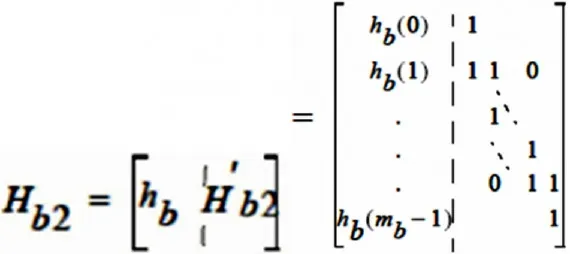
LDPC 码是系统码，整个码字可以分成信息部分S 和校验部分P。编码的过程就是从一个码字的信息位算出校验位的过程。为了方便描述，信息部分S 被分成kb=nb-mb个z 比特组：

u=[u（0）u（1）…u（kb-1）]T

其中每个元素u 表示如下列向量：

使用基础矩阵Hb，校验位P 被分成mb个z 比特组：

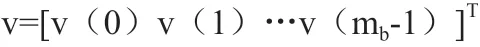
其中每个元素v 表示如下列向量：

编码过程分成两步：

（1）初始化：计算v（0）；

（2）递归：从v（i）计算v（i+1），0≤i≤mb-2。

v（0）可以通过对Hb的行求和得到：

这里1≤x≤mb-2，表示Hb中的惟一一个非负和非成对元素的行索引，其中Pi表示循环右移i 位的z×z 的单位阵。通过上面方程可以解出v（0）。

考虑到H'b2的结构，可以得到以下递归：

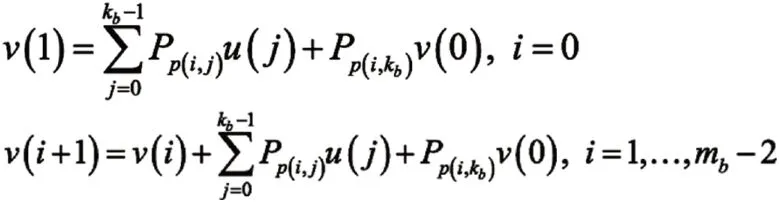
这里P-1=0zxz

（1）计算v（0）

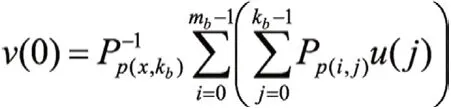
在计算v（0）的过程中，将前mb-1个中间值存储，i=0，1，...mb-2。（mb=4，kb=28），那么v（0）可以表示如下：

（2）计算v（1）

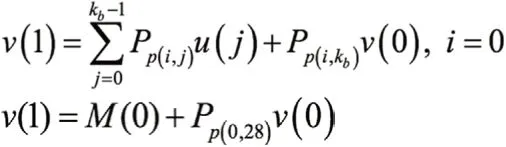
由于P（0，28）=0，上式可化简为：

v（1）=m（0）+v（0）

（3）计算v（i+1）

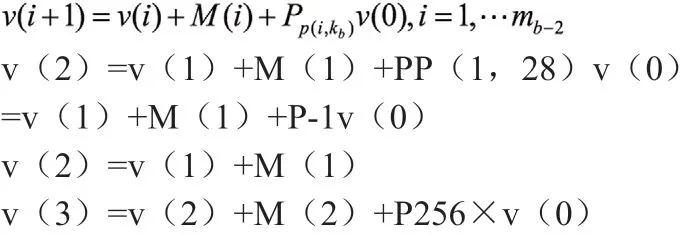
模版矩阵Hb可以分成两部分Hb1和Hb2，其中Hb1对应系统位部分，Hb2对应校验位部分矩阵划分：

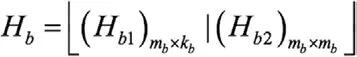
3.1 概率域BP 算法

LDPC 码的标准译码算法是BP 算法（Bel ief Propagation 算法，也叫Message Passing 算法）。下面将详细介绍该算法，该算法是基于定义LDPC 码奇偶校验矩阵H（m×n），n 为LDPC 码的码长，m 为校验位长度。下面介绍一下后面用到的符号：

N（m）={n：Hmn=1}表示参加第m 个校验方程的所有比特的下标的集合；M（n）={m：Hmn=1}表示第n 个比特参加的所有校验方程的集合；N（m） 表示参加第m 个校验方程的除去第n 个比特所有比特的下标的集合；M（n）m 表示第n 个比特参加的除去第m 个校验方程所有校验方程的集合；yn为信道软信息；qbn为译码输出软信息，即P（xn=b）；为译码输出硬判决；qbmn表示从第n 个变量节点到第m 个校验节点关于xn=b 的概率信息，即在除了第m 个校验方程外，比特节点n 参加的其他校验方程和信道软信息yn给出的xn=b 的概率；rbmn表示从第m 个校验节点到第n 个变量节点的信息，即在第m 个校验方程的除去第n 个比特以外其他比特的概率用{qmn'}n'≠n 给出和xn=b 的情况下第m 个校验方程通过的概率。

BP（Believe Propagation）置信传播算法是目前应用最多的也是性能比较好的一种算法，它的一般译码过程如下[1]：

概率域BP 算法步骤：

（1）初始化

按照下面公式初始化q0mnand q1mn：

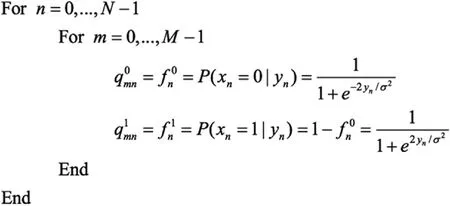
（2）校验节点更新

按照下面公式更新r0mn和r1mn：

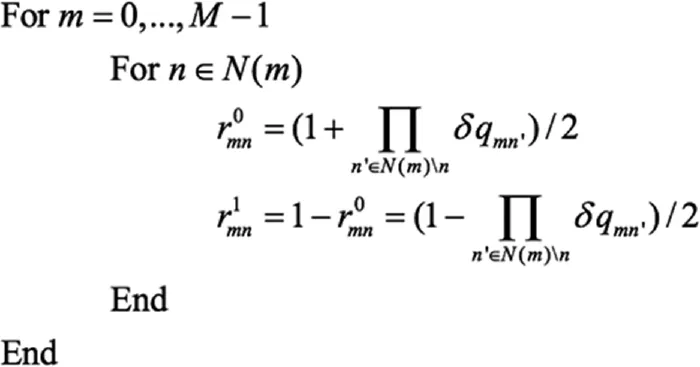
其中，

（3）变量节点更新

按照下面公式更新q0mn和q1mn：

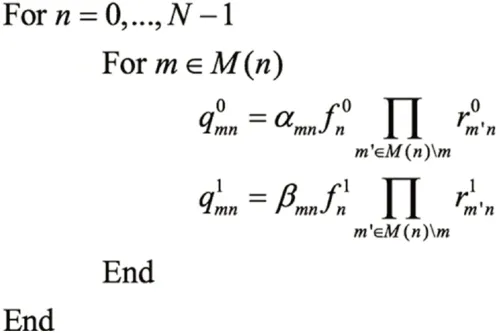
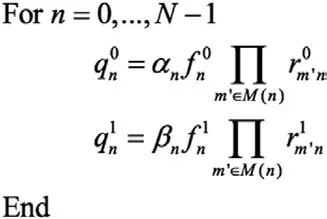
（5）迭代中止判断

按照下面公式对译码输出数据进行硬判决：

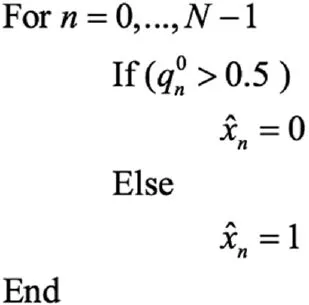
3.2 对数域BP 算法

概率域BP 算法涉及到大量乘法运算，运算量大，并且动态范围大数值稳定性不好，在实际应用中通常使用对数域BP 算法。

对数域BP 算法将使用下面对数似然比[2]：

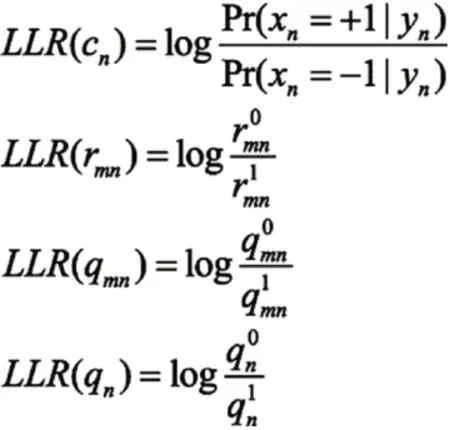
3.3 最小和算法

Min-Sum 算法和标准对数域BP 算法的差别在两点：

第一，直接用信道软信息yn对码字比特的对数似然比进行初始化，不需要信道噪声方差信息σ2，也就是不需要估计码字所对应的信道信噪比。

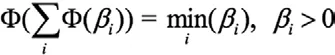
其中

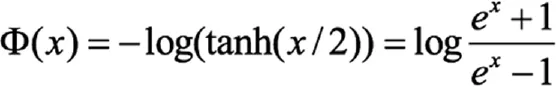
在AWGN 条件下，Min-Sum 算法比标准对数域BP 算法有大概0.3dB 左右的性能损失，并且在低信噪比条件下迭代次数也要多一些。性能损失和LDPC 码的行重量有关，行重量越大近似运输误差越大，性能损失也越大。

3.4 修正最小和算法

其中常数A 和LDPC 码的校验矩阵H 的行重量有关系，可能取值为0.6～0.9，确切的数值要通过仿真来确定。

在AWGN 条件下，修正最小和算法性能要比标准BP 算法性能大概差0.1dB，如图2所示：

3.5 分层BP 算法

分层译码算法和标准BP 算法的区别在于在迭代中当更新完H 矩阵中每一行非零元素对应的LLR（rmn）后马上更新该行每个非零元素对应列所有非零元素对应的LLR（qmn），然后再对H 矩阵中的下一行进行译码。该算法和标准BP 算法比可以加快译码收敛，节约迭代次数以提高吞吐量，最好情况下可以节约一半的迭代次数。

分层对数域BP 算法步骤：

（1）初始化

图2 修正最小和算法性能与标准BP算法性能比较

按照下面公式初始化LLR（qmn）：

（2）校验节点和变量节点更新按照下面公式更新LLR（rmn）：

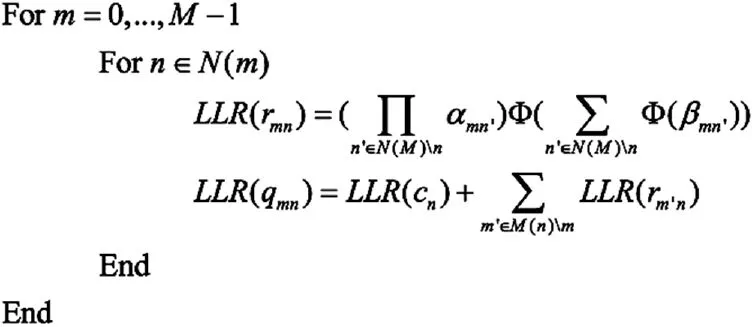
其中：

（3）LLR（qn）更新

按照下面公式更新LLR（qn）：

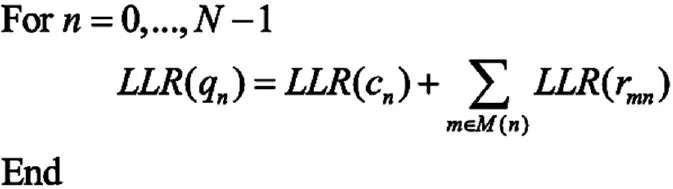
（4）迭代中止判断

按照下面公式对译码输出数据进行硬判决：

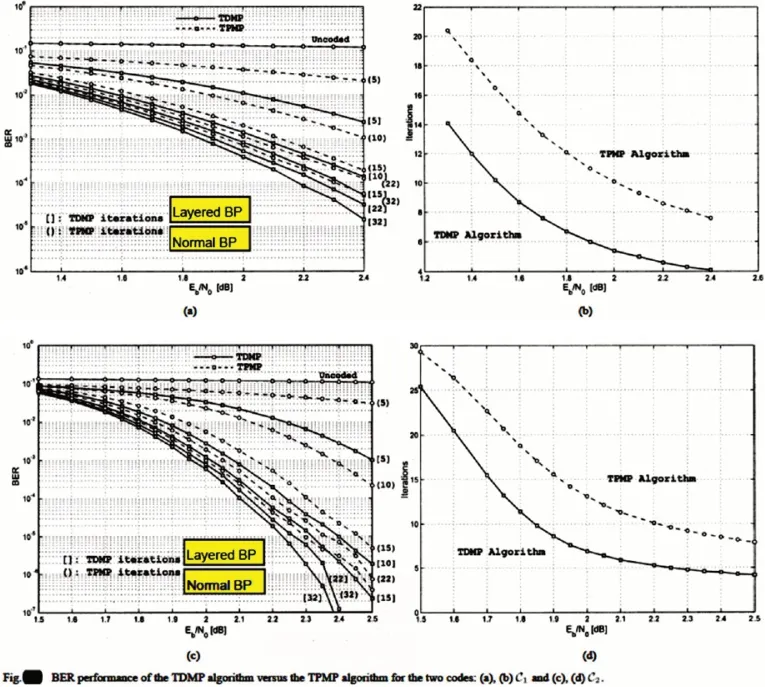
图3 分层BP译码算法和普通BP译码算法的性能比较

4 LDPC 译码实现框架

LDPC 译码采用简化的分层译码算法，这使得LLR（qmn）不直接存储，降低对硬件资源的需求，整个译码流程如图4所示。

（1）初始化。初始信息LLR（qn）直接用信道软信息yn 对码字的比特软信息进行初始化，LLR（qn）=yn，并且按照扩展因子512 个LLR（qn）值为一组，存入LLR RAM 中。同时R Storage Memory 也进行初始化，校验信息即外信息LLR（rmn）=0。

（2）更新变量节点和外信息。R Storage Memory 将未更新的外信息LLR（rmn）信息读出，与交织后的比特软信息qn进行LLR（qmn）=LLR（qn）-LLR（rmn）运算，变量节点信息LLR（qmn）输入到CNU 模块计算出外信息，对应的计算公式为LLR将此外信息一路存回至R Storage Memory 中，覆盖对应的旧的LLR（rmn）。一路送入至对应的加法器计算出新的比特软信息，LLR（qn）=LLR（qmn）+LLR（rmn），新的比特软信息经过反交织模块处理后存入LLR RAM 中，更新qn。

（3）迭代终止判断。当完成一次迭代后，我们根据=0来判断译码是否结束，满足或达到最大迭代次数结束整个译码过程，否则跳到（2） 继续迭代。

6 结束语

通过仿真，考虑实现的难度我们采用分层BP 算法，结果表明所实现的文中LDPC 编译码算法的性能相比于其他编码方式在信噪比上有了很大的提高，有效地提高了系统的有效通信距离。