水合物分解条件下海底黏土质斜坡破坏实验模拟

（大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连116024）

天然气水合物（又称可燃冰）是一种在低温高压条件下由水和天然气（主要是CH4、C2H6等）形成的笼形晶状化合物，广泛分布于深海海底沉积物和陆地永久冻土带[1].据估算，全球天然气水合物中蕴藏的天然气总量相当于全球已探明传统化石燃料（煤炭、石油和天然气）总碳量的两倍，被普遍认为是21世纪最具潜力的新型能源之一[2].

自然温压条件变化、油气开采和水合物开采会引起水合物沉积层中水合物分解，并释放大量的气体，气体的存在会严重影响海底斜坡的稳定性.在海底高压条件下气体被压缩，孔隙压力会迅速增加，降低土体的有效应力，有可能导致大规模的海底滑坡等灾害，毁坏海底电缆或海洋石油钻井平台等海底工程设施[3－5].因此，针对水合物分解条件下海底斜坡破坏的研究具有重要的现实意义.

文献[6－8]利用极限平衡法分析了水合物分解条件下海底斜坡的稳定性.文献[9－11]综合考虑热场、渗流场、力场与化学场，提出了水合物分解热－渗流－变形－相变耦合模型，用于研究水合物开采的产能预测，开采过程中地层的沉降等问题.虽然数值分析方法应用较为广泛，但可靠的计算结果依赖于对海底斜坡变形破坏机制的深入认识，并据此作出合理的简化假设.

物理模型实验是岩土工程中一种重要的研究手段，可以直接观测和记录海底斜坡的变形和破坏过程，是深入研究水合物分解引起海底斜坡变形破坏机制的有效途径.文献[12－14]对在不同边界条件和加热方式下水合物分解后引发的层状和喷发破坏进行了分析.文献[15]基于透明土技术，探讨了水合物分解对黏土性质的影响以及流体逸出结构的形成过程.文献[16]和[17]通过离心机模型实验，研究了水合物分解后沉积物力学性质和地层滑塌特征.文献[18]和[19]采用通气的方式，分别研究了水合物分解后土体与气泡的相互作用以及对海底粉砂土海床的破坏规律.目前，物理模型实验多以人工合成、厌氧发酵、通气等方式模拟水合物分解，主要介质为粉砂.而根据地质调查资料，在南海陆坡区，随着水深的增加，海底沉积物颗粒逐渐由粉砂、粉砂质黏土变为深海黏土[20]，对于水合物分解条件下海底黏土质斜坡变形破坏的模型实验研究鲜见报道，对其内部变形破坏过程认识不足，变形破坏机制仍不清楚.此外，水合物分解引起海底斜坡破坏的临界压力研究尚处于空白.

基于此，以典型地质调查资料为依托，概化海底黏土斜坡几何模型，采用通气的方式模拟水合物分解后气体对海底斜坡的影响，开展多组模型实验.结合图像测量技术，研究了不同的土体强度、水合物埋深、气体流量及分解范围等组合条件下的海底斜坡破坏特征，综合分析了坡面及坡体内部的变形破坏过程，初步揭示了模拟水合物分解条件下海底斜坡的变形破坏特征；在此基础上，采用极限平衡方法，建立了海底斜坡破坏时的临界气体压力解析式，从理论上计算了斜坡变形破坏过程中的临界气压值.本文研究为深入认识水合物分解条件下海底黏土质斜坡的变形破坏机制，发展稳定性分析理论和评价方法提供有益参考.

1 实验介绍

1.1 相似比尺确定

正确的相似比尺对模拟真实海底边坡破坏过程非常重要，前人对于模型实验的相似关系进行了详尽的研究[21－23].要想获得成功的模型实验，模型需要满足几何学相似、运动学相似和动力学相似.

几何学相似意味着模型与原型在相应长度方向上成比例，即

式中：rL为长度比尺；L为长度；下标m、n分别表示模型和原型.

运动学相似要求模型与原型相应的时间成比例，即

式中：rt为时间比尺；t为时间.

动力学相似要求相应的质量（M）成比例，以及作用在相应点上的力（F）成比例，且具有相同的方向，即

式中：ra为加速度比尺；a为加速度.由于模型和原型均处在常规重力场内，加速度a相同，即ra＝1.另外，完全的动力学相似还需满足：

式中：Ra表 示 Ramberg数[24]；Re表 示 Reynolds数；Fr表示Froude数；下标g、s、i、v分别表示重力、表面力、惯性力、黏滞力.实验过程很缓慢，惯性力可以忽略，因此只需满足：

根据以上相似关系，得出对应参数的相似比尺，具体关系如表1所示.实验选取相似比尺N＝1 000，依据表1的相似关系可以将模型实验放大到真实尺度.

表1 参数的相似关系Tab.1 Scaling relations of parameters

1.2 实验装置

1.2.1 气体压力控制器 实验采用自主研发的气体压力控制装置，严格控制气体流量，确保实验的高度可重复性.设备内部构造和外观如图1所示，由限流控制阀、比例阀、流量计、压力缸、控制面板和监控单元构成.该仪器同时具有压力控制和流量控制两种模式.可实现恒定压力（0～1MPa）与恒定流量（0～100mL／min）的精确控制.仪器可通过外接气源实现不间断通气，避免了传统压力缸体积小和通气量小的限制.为解决气体压力监测的问题，在出气孔处布置了气体压力传感器，可实现对通气压力的实时监控.

1.2.2 测量系统 为避免对土体的扰动，实验均采用非接触式的测量手段.采用激光位移传感器测量坡面位移，通过粒子图像测速法（PIV）观测斜坡内部侧向位移场.其中，激光位移传感器固定在支架上，其测点位于通气点正上方，侧面布置GoPro高速运动相机，用于观测土体侧面位移场，实验具体布置如图2所示.

图1 气体压力控制器Fig.1 Air pressure controller

图2 测量系统实验布置图Fig.2 Experimental setup of the measuring system

1.3 实验方案

实验主要目的是研究水合物分解后在气体作用下海底斜坡变形破坏的特征，不考虑水合物分解的过程.目前真实条件下水合物分解数据较少，且获取困难，但现有数值模拟和实验结果[25－26]均显示在水合物分解过程中，水合物的剩余量与总产气量随时间呈线性分布.因此假定水合物的分解速率是恒定的，用恒定流量通气的方式模拟水合物分解.另外，由于高岭土性质均一，被广泛用于模拟海底黏土边坡，所以采用高岭土作为海洋饱和软黏土的模拟材料.依据南海海底沉积物强度测试数据[27]，利用加载固结的方式，制备两种不同强度的土体用于实验，具体土体参数如表2所示.

此外，地质调查[28]表明，南海北部陆坡区坡度为2.5°～12.8°，由于模型箱尺寸限制，实验选取概化的斜坡坡度为10°.另外，选取气体流量分别为35.1和43.5mL／min，水合物埋深分别为5和2.5 cm，分解范围分别为5和3cm.由此开展不同土体强度、气体流量、水合物埋深及分解范围组合形式的多组模型实验，具体实验方案如表3所示.

表2 土体参数Tab.2 Soil parameters

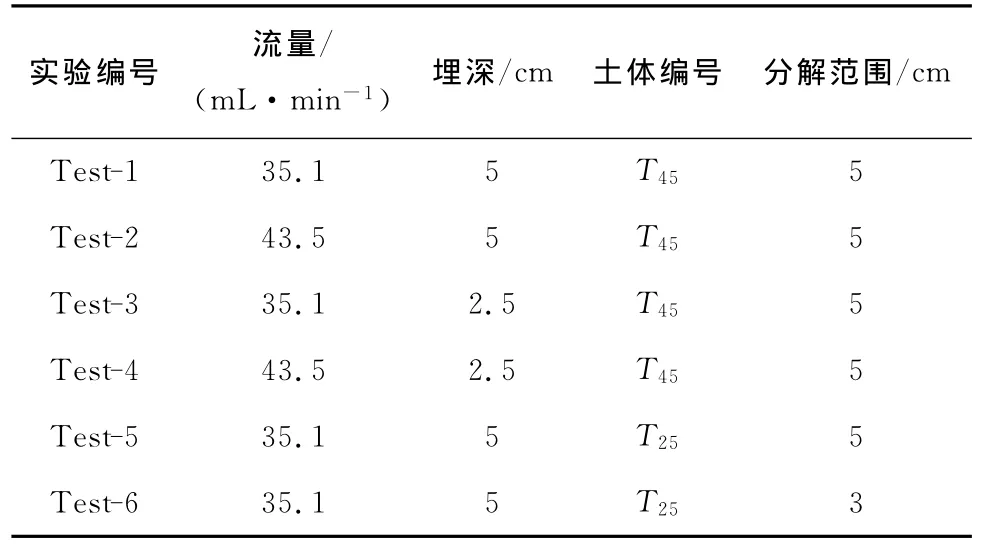
表3 实验工况Tab.3 Experimental conditions

1.4 实验步骤

第1步 预埋通气管道和砂层.为防止气体沿侧面有机玻璃板与土体交界面逸出，将出气点布置在模型箱正中，距离侧面有机玻璃板2cm处并固定.在管道出气孔布置球形砂层，使气体能够均匀地向四周扩散，通过改变砂层直径达到模拟不同水合物分解范围的目的.

第2步 制备土样.配置初始含水率为120%（约2倍液限）的土样，使用真空搅拌釜在－0.08 MPa条件下搅拌2h，制备出充分混合的饱和土试样；然后缓慢将高岭土倒入模型箱中.为减小边界效应的影响，在倒入高岭土前，在模型箱内壁均匀地涂抹一层凡士林.然后分别在45和25kPa压力下固结，变形稳定后撤去压力.

第3步 制备边坡模型.打开模型箱侧面有机玻璃板，均匀地撒上一层示踪粒子.之后再放入固结仪下固结24h，使土体与有机玻璃板充分贴合.固结完成后，进行削坡工作.

第4步 开始实验.为避免外部光源干扰，削坡完成后，将模型箱放入实验槽内，在实验过程中保持封闭状态.连接气源，打开气体压力控制器，待流量稳定后，接通气管，向土体内部通气，直至斜坡破坏，完成实验.

2 实验结果与分析

2.1 坡面位移特征

实验测试结果如图3所示，p为通气压力，s为坡面位移，t1为通气时间.由于不同工况下实验的持续时间差异较大，为方便比较，将所有曲线时间轴无量纲化.从图3中可以看出，对于不同工况通气压力和坡面位移变化趋势基本一致.对于通气压力，实验开始之后，由于此时通气量较小，气体均匀地扩散到孔隙中，压力没有明显变化.随着通气量的增大，气体开始被压缩，通气压力上升，达到峰值后逐渐减小，最后突降为0，总体呈抛物线型.在这个过程中伴随着坡面位移的变化，可分为4个阶段：① 位移平稳阶段：实验开始时，由于通气压力较小，位移没明显变化；② 位移稳步增长阶段：通气压力上升，土体开始出现位移，但增长速率缓慢；③ 位移加速增长阶段：随着通气压力的继续上升，到达某一压力值时，坡面位移随通气压力变化转变到位移加速增长阶段，定义此时的压力为临界气体压力值；④ 位移峰值阶段：压力突降为0时，位移达到峰值，并保持稳定.从图中可知，对于 Test－1～Test－6，通气压力的响应时间（以无量纲表示）分别为0.317、0.514、0.167、0.117、0.088、0.251，坡面位移的响应时间分别为0.489、0.604、0.189、0.164、0.102、0.313.通气压力的响应时间均早于坡面位移的响应时间，符合一般规律.

图3（a）为不同土体强度条件下的通气压力与坡面位移的测试结果.Test－1测得的通气压力最大为18.1kPa，坡面位移最大为6.87mm.Test－5测得的通气压力最大为7.7kPa，坡面位移最大为22.58mm.强度对压力累积和坡面位移的影响显著，在低强度土体中，较小的通气压力下就能产生较大的相对位移.

图3（b）为不同埋置深度条件下的测试结果.相对于 Test－2得到的最大通气压力18.3kPa，Test－4测得的最大通气压力为12.1kPa，即随着埋深的增加，通气压力增大.对于坡面位移，Test－2测得最大值为3.95mm，Test－4测得最大值为12.47mm，即随着埋深的增加，坡面位移减小.这是因为随着埋深的增大，气体在扩散过程中需要克服更大的上覆土压力.

从图3（c）可知，Test－3测得的最大通气压力为8.8kPa，最大坡面位移为6.54mm.与 Test－4测试结果对比可得：随着流量增加，通气压力上升，坡面位移增大.根据理想气体状态方程，在有限体积的情况下，流量的增加意味着物质的量增大，所以通气压力会上升.而在相同埋深和相同强度条件下，通气压力的增大，自然会导致坡面位移的增加.

由图3（d）可知，Test－6测得的最大通气压力为11.6kPa，最大坡面位移为17.91mm.与 Test－5测试结果对比可以看出：分解范围越小，通气压力越大，坡面位移较小.这是因为分解范围变小，相当于气体的容积变小，同样根据理想气体状态方程，在相同流量下压力会变大.而容积变小会导致气泡的作用面积减小，相应的作用力会减小，所以坡面位移会变小.

图3 测试结果对比Fig.3 Comparison of experimental results

2.2 坡体变形特征

实验结束时刻的累积位移矢量图及影响范围如图4所示.x为水平位置，y为竖直位置.这里需说明由于设备故障，未获得Test－1的位移矢量图，但由图3（a）可知，Test－1的坡面位移测试结果符合上述分析的位移变化规律，而坡面位移是坡体内部变形的外在体现，因此Test－1的位移矢量图也应符合总体变形规律.以下对Test－2～Test－6工况进行对比分析.

图4 实验结束时刻位移矢量图Fig.4 The displacement vector diagrams at the end of the experiment

由图4可知，坡体位移矢量基本上可以按照破坏面分为两部分：一部分是破坏面以下的土体，该部分土体位移量相对较小，且没有固定方向；另一部分是在破坏面以上的土体，该部分土体位移量相对较大，且通气点正上方位移最大，方向基本垂直于原始坡面.以通气点中轴为界，位移量向两边逐渐减小，方向向两边逐渐发散.

由图4还可得出，不同因素对坡体变形特征的影响.对比 Test－2与 Test－4工况，对于 Test－2最大合成位移为4.02mm，在坡面的影响范围宽99.50 mm；对于 Test－4最大合成位移为12.66mm，在坡面的影响范围宽70.28mm；随着埋深增大，相对位移变小，这与上述结论相符.另外，埋深越深，影响范围越大.对比 Test－3与 Test－4工况，对于 Test－3最大合成位移为6.57mm，在坡面的影响范围宽76.55mm；随着流量增大，相对位移变大，但影响范围无明显差异.对比 Test－5与 Test－6工况，对于Test－5最大合成位移为23.05mm，在坡面的影响范围宽108.37mm；对于Test－6最大合成位移为18.21mm，在坡面的影响范围宽147.28mm.随着分解范围增大，相对位移变大，但影响范围变小.

2.3 变形破坏过程分析

通过多组模型实验，得出上述坡体变形破坏特征.结合通气压力、坡面位移的变化规律及斜坡破坏过程不同阶段的实物图（以Test－6工况为例），将整个斜坡变形破坏过程概化为4个主要阶段，如图5所示，t2为对应的时间节点.

（1）气压累积阶段.水合物开始分解，但此时分解量较小，气体均匀地扩散到周围孔隙中，通气压力基本为0，坡面位移无明显变化，如图5（a）所示.

（2）土体弹性压缩阶段.随着分解量不断增加，气体被逐渐压缩，通气压力上升，土体被弹性压缩，位移开始缓慢增长，如图5（b）所示.

图5 不同阶段斜坡破坏特征（Test－6）Fig.5 Characteristics of slope failure at different stages（Test－6）

（3）斜坡破坏隆起阶段.随着通气压力的不断增加，斜坡土体被抬升，坡面产生隆起；当通气压力大于气体临界压力时，土体内部产生张拉裂缝，且裂缝沿着近乎平行于坡面方向扩展，位移快速增长，定义此时的气体压力为临界压力，如图5（c）所示.

（4）变形稳定阶段.通气压力的作用下，内部裂缝不断扩展直至贯通，压力突然释放，变形达到峰值，并保持稳定，如图5（d）所示.

3 临界压力分析

为求解斜坡破坏时的临界压力，运用极限平衡法对斜坡破坏时的临界状态进行分析.由于实验采用的是饱和黏土，内摩擦角φ＝0°.根据朗肯土压力理论，破坏面与坡面呈45°，则土体发生破坏时的临界状态受力如图6所示.

图6 临界状态斜坡受力图Fig.6 The forces acting on the slope at the critical state

由z方向受力平衡可得

式中：W为破坏区域土体的自重；T为破坏面上剪应力合力；P为作用在上部土体气体线压力；l为初始分解区域的宽度；α为斜坡坡度.

破坏区域土体自重可表示为

式中：γ为上部土体的重度；d为水合物的埋置深度.假设土体的剪切强度符合摩尔－库伦准则，则土体内部某一点的临界应力状态为

式中：τ为作用在剪切面上的剪切应力；σ为作用在剪切面上的有效法向应力；c为土体的黏聚力.

则破坏面上剪应力合力为

将各实验具体参数代入式（11），计算结果如表4所示.

将式（8）和（10）代入式（7）可得斜坡发生破坏时的临界压力为

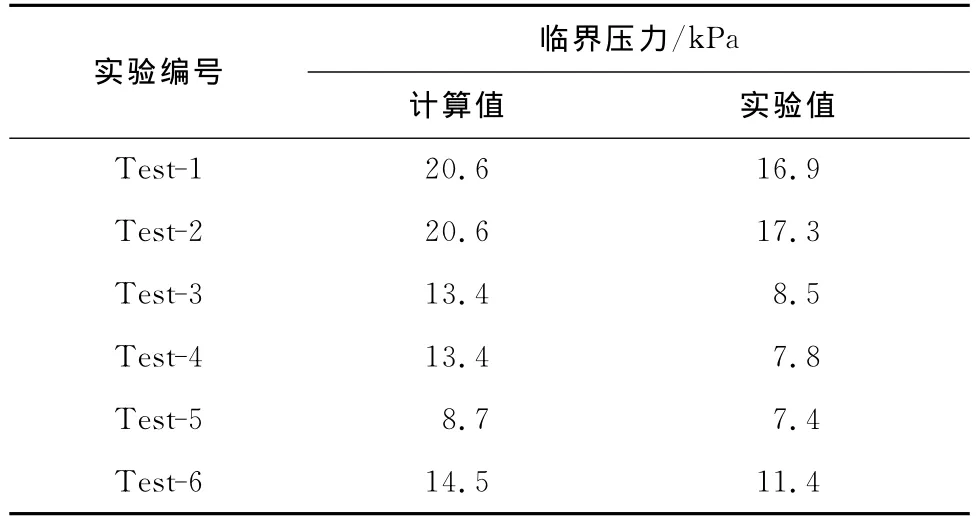
表4 临界压力计算结果与实验结果Tab.4 Calculated and experimental results of critical pressure

Test－1～Test－6计算结果较实验结果偏大，偏差在20%左右，这是因为根据上文所述，出气点距侧面有机玻璃板有一定的距离，当侧面观察到裂缝时，说明出气点处已经发生破坏，此时真实的分解范围lr发生变化，由于裂缝扩张使得lr＞l；另一方面，观察实验图像可得，当侧面出现裂缝时，所假设破坏面并未全部进入临界状态.这两方面的原因导致计算结果较大.计算结果虽大于实验结果，但可在一定程度上反映临界压力的真实水平，为海底黏土质斜坡稳定性评价提供参考.

4 结论

（1）强度对压力累积和坡面位移的影响显著，在低强度土体中，较小的通气压力下就能产生较大的相对位移；随着埋深的增加，通气压力增大，坡面位移减小；随着流量增加，通气压力上升，坡面位移增大；随着分解范围增大，通气压力减小，坡面位移增大.

（2）水合物分解条件下海底斜坡变形破坏过程可概化为4个阶段：气压累积阶段；土体弹性压缩阶段；斜坡破坏隆起阶段；变形稳定阶段.前两个阶段位移变化较小，后两个阶段位移快速增长直至稳定，此时可观察到明显的裂缝，方向平行于原始坡面.

（3）虽然气体临界压力计算结果与实验结果偏差在20%左右，但可在一定程度上反映临界压力的真实水平，可为海底斜坡稳定性评价提供参考.