多约束条件下基于稀疏迭代势场法的无人艇局部避碰方法

文龙贻彬，胡常青,2,3，赵荣利，徐宇新

(1.北京航天控制仪器研究所，北京 100039；2.中国地质大学（北京）工程技术学院，北京 100083；3.青岛海洋科学与技术试点国家实验室，山东 青岛 266237)

0 引 言

无人水面艇（以下简称无人艇）目前在国内外军事和民用领域的应用日渐增多，而无人艇能够自主航行的关键则取决于路径规划技术[1]。

与其他路径规划方法相比，人工势场法在路径规划和避障领域有着极其广泛的应用，这是因为其理论较为简单、易于实现从而极具吸引力[2]。除了建立吸引/排斥力模型外，许多其他势场函数方法也正在被研究，这些方法能够非常有效快速地规划出路径，但都存在局部最小值的问题[3]。

这个问题会导致以下几种情况发生：

1）存在陷阱区域；

2）在相近的障碍物群中不能识别路径；

3）在障碍物前震荡；

4）在狭窄通道中摆动；

5）障碍物附近目标不可达。

为了克服这些问题，目前国内外研究者针对人工势场法有如下几种改进方式：结合基于搜索规划器的路径规划方法。如采用波前规划器来克服局部最小值问题[4-5]。改进势场函数，定义一个只有一个局部最小值的势场函数，从而解决上述问题。如斥力势场函数改进模型[6]。加入应激行为，来摆脱极值点，重新向终点前进。如加入一个随机扰动[7]。加入中间点[8]。利用几何方法重新规划路径，摆脱局部极小点[9]。结合智能算法的路径规划方法，如基于混沌优化改进的人工势场法[10]。通过蚁群算法来不断优化人工势场法获得的路径[11]。结合遗传算法来改进人工势场法来获得最优路径[12]。

上述方法可以解决局部最小值点导致的问题，但也存在着规划过于复杂等问题。

2011 年，Hossein Adeli 等提出了一种迭代势场算法[13，能够很好地解决移动机器人的路径规划问题，并依然保持了算法理论的简洁性和易于实现性。但上述方法存在需要调参、耗费较大的计算资源等缺点，不适用于局部路径规划。

本文提出一种基于栅格法的稀疏迭代势场方法。通过稀疏点约束方法和构建一种比传统迭代势场算法更加简单的势场函数，提高算法运行速度，并解决栅格法离散化所带来的缺陷（限制了路径方向变化只能为π/4 的倍数，会导致无人艇不必要的运动转向），不但能规划一条任意角度的最短路径，还大幅减少了计算时间。此外针对无人艇局部路径规划需要满足海事规则的特点，建立了海事规则和转向避碰模型，最终让无人艇实现实时、快速、安全地避碰，规划出来的路径符合无人艇的运动特性且能够通过改变安全距离的方式，实现场景自适应功能。

1 传统迭代势场算法

1.1 栅格法

利用栅格法对环境进行建模，将工作空间划分为一系列具有障碍物信息的正方形栅格网络单元，如图1 所示。图中黑色区域为可行区域，白色区域为不可行区域。栅格中的每一个单元格就代表一个路径点。但栅格法的离散化建模方法，限制了无人艇的路径方向变化只能为π/4 的倍数。当为稠密路径点时，S0无法直达P1，需要S0→S1→P1或S0→S8→P1。

1.2 势场函数

势场函数如下式：

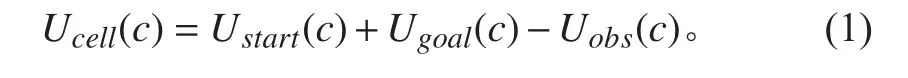
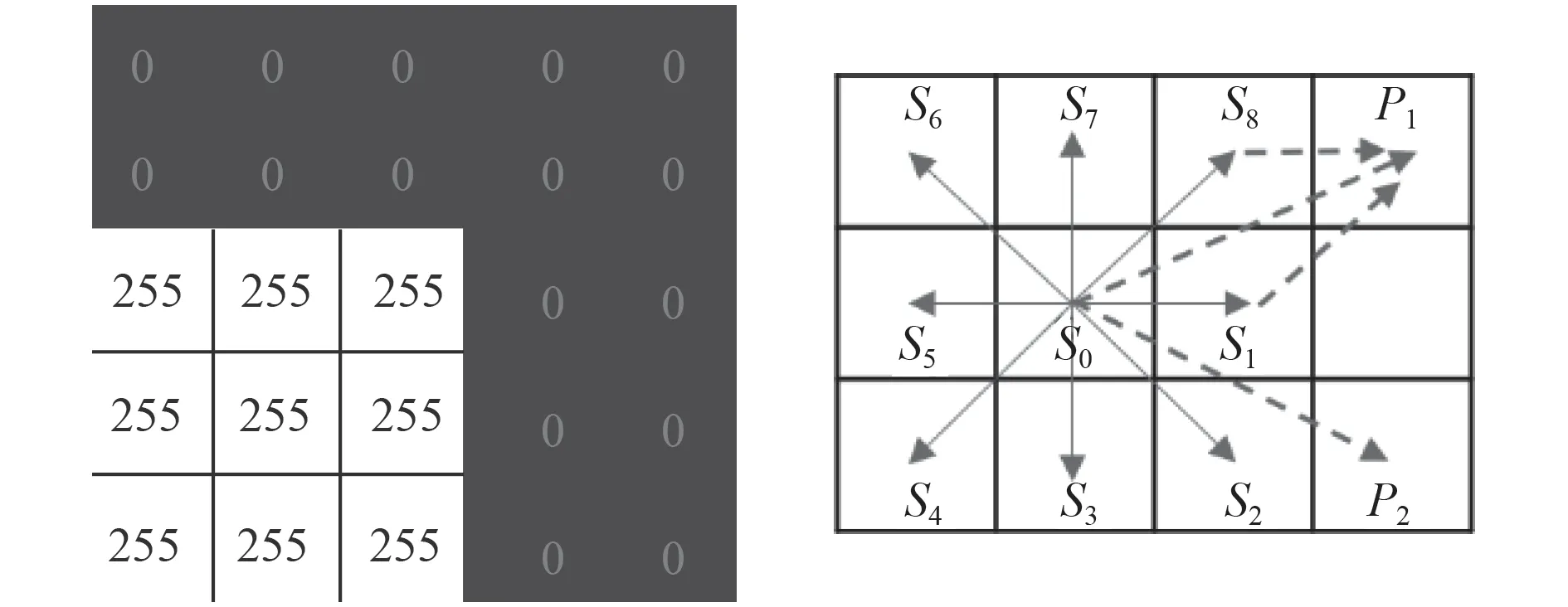
图 1 栅格法环境建模和栅格法离散化缺陷Fig.1 Environment modeling with grid method and Discretization defect of grid method

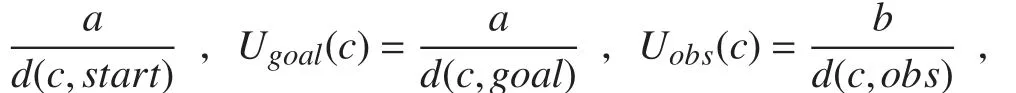
1.3 迭代二分搜索

最优路径是由一系列最优点组成，只要得到每一个最优路径点，就可以得到最优路径。

根据式（1），对可行区域中每一点计算势能值，并存入一个集合中。

然后进行最优点寻找，并不断进行迭代二分搜索，直至生成一条最优路径，如图2 所示。

图 2 迭代二分搜索示意图Fig.2 Iterative binary search diagram

迭代势场算法可以直接得到一条全局最优路径（此处的最优路径是指考虑到障碍物排斥势场的最优路径，而非最短路径），但其存在3 个缺陷。

1）需要计算d(c,obs)

为了得到势场函数，需要计算 d(c ,obs)项的大小，即使利用Brushfire 算法来计算，也需要对整张地图进行一次遍历，当地图较大时，计算 d(c ,obs)将会消耗一定时间。

2）需要迭代多次

为了得到考虑障碍物的排斥势场的最优平滑路径，需要迭代足够多的次数，但当迭代次数过多时，就会变成稠密点路径，将会出现栅格法离散化问题，如图1 和图2（d）所示，此外运行时间也会大大增多。

3）需要调参

该算法可以通过调整 a ， b的值，改变安全距离的大小。但其缺点是当场景或环境地图不同时，需要基于经验进行调参才能改变安全距离的大小，且无法得到准确的安全距离值，无法满足无人艇局部避碰场景自适应的要求。

2 改进迭代势场算法

为了解决上述缺陷，本文提出了一种改进迭代势场算法。

2.1 改进势场函数

改进势场函数如下式：

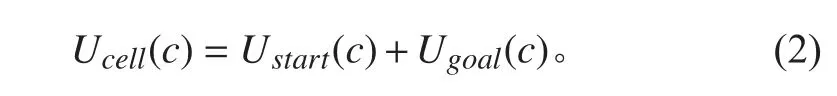
其中：各项含义等同于式（1），但是舍弃了Uobs(c)项，即势场函数只考虑起点与终点的吸引力。

这样的好处是减少了计算 Uobs(c)项所耗费的时间，从而更好地满足局部路径规划的实时性需求。

另一方面在改进势场函数的基础上，通过建立安全模型可以得到一条量化了安全距离的最优路径，这样就解决了传统迭代势场法需要调参的问题，从而让无人艇具备自适应场景的能力。同时也解决了由于舍弃了 Uobs(c)项，导致路径离障碍物过近的问题。

基于改进势场函数进行迭代二分搜索得到的点应为最优点Poptimal，因为这个点只在可行区域中进行寻优且确保了路径的存在。此外，由于改进势场函数不考虑障碍物的排斥力，当障碍物挡住路径时，为了保证迭代路径点相互联通，此时最优点必将出现在障碍物边缘。定义这些出现在障碍物边缘的最优点Poptimal为关键点Pkey，易知最短路径一定可以由Poptimal中的某些点联通而成。

2.2 稀疏点约束

为了防止出现栅格法离散化问题和提高计算时间，在算法中加入稀疏点约束。

稀疏点约束由联通约束与最短路径约束组成。

首先加入联通约束。采用Straight of line 算法作为迭代终止条件，即只需最优点间两两联通即可，如图3 所示。这样得到的最优点数量大幅减小，从稠密点减少为重要联通点。

图 3 重要联通点Fig.3 Important connecting points

联通约束的目的是得到少量的点序列来完成路径规划任务，其搜索量和时空开销会减小,收敛速度变快。不但减少了计算时间，而且得到任意角度的路径。

针对重要联通点，再加入最短路径约束。

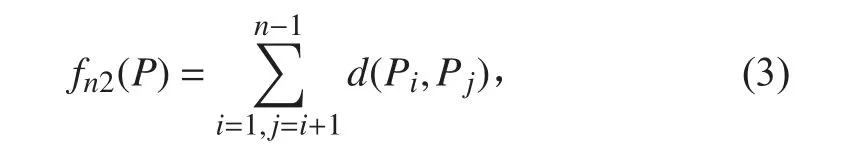
式中： d(Pi,Pj)为相邻重要联通点的欧式距离；n 为重要联通联通点个数。

采用Floby 算法对下式进行求解。

将求解出来的点定义为稀疏点Psparse，从而得到一条由Psparse连接而成的最短路径，如图4 所示。

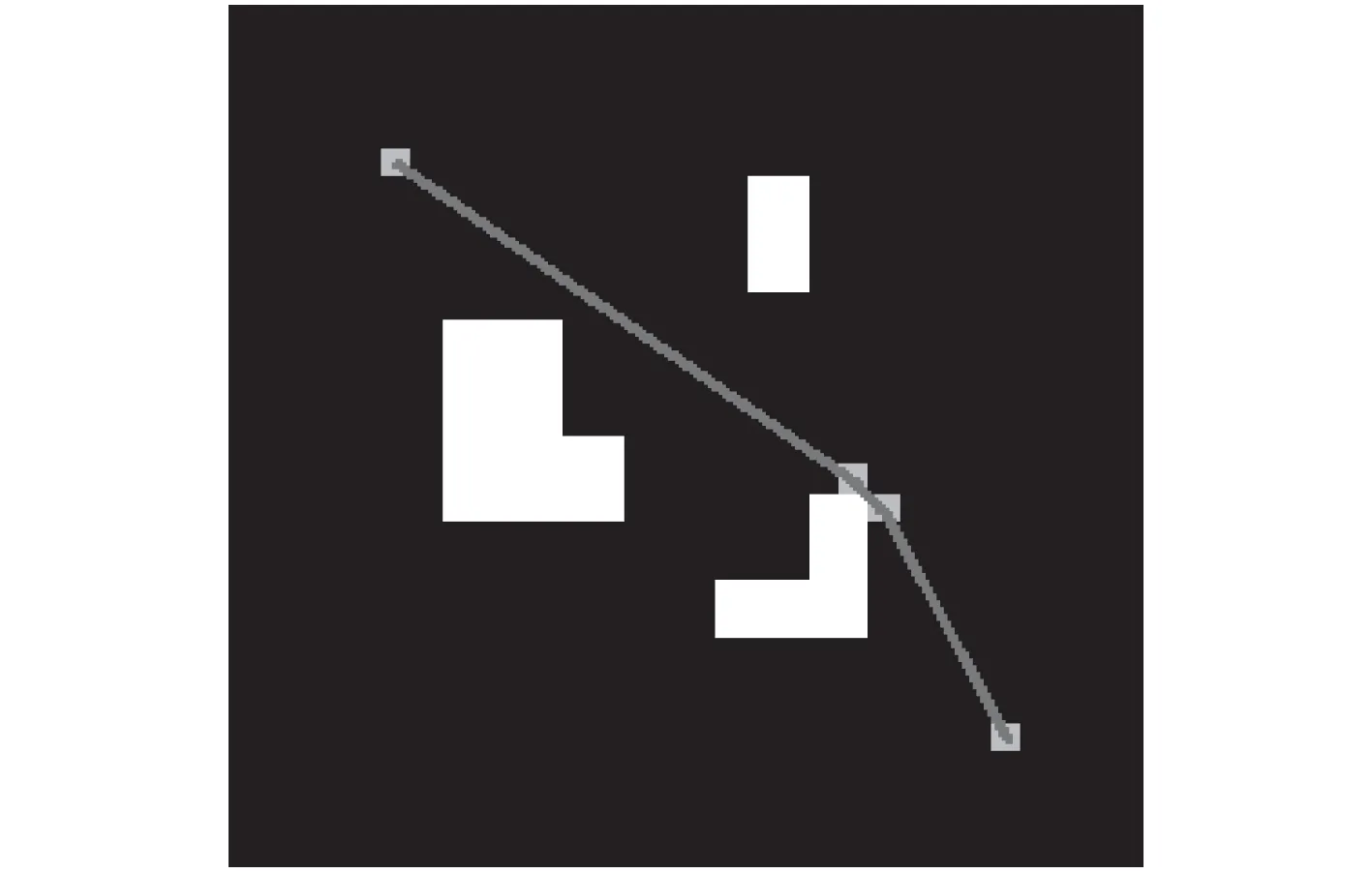
图 4 稀疏点Fig.4 Sparse points

此项约束不但能够将重要联通点优化为稀疏点，而且可以规划出最短路径。路径最短也就可以认为避开障碍物的时间最少（在符合无人艇运动学的情况下），从而满足了局部路径规划的时间需求，能够实现快速避碰。

2.3 安全距离约束

基于稀疏点约束，得到一条由Psparse连接而成的最短路径。由于Psparse都在障碍物边缘，容易导致危险。因此加入安全距离约束，确保路径中的每一个路径点离障碍物有一定的距离，在快速避碰的同时确保安全。

安全距离约束为：

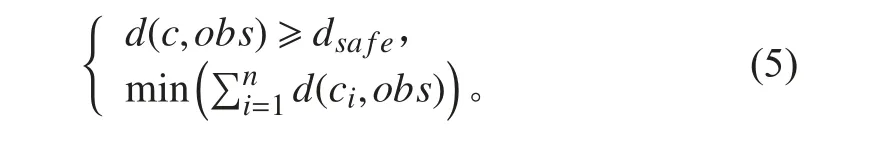
式中： dsafe为安全距离； d(c ,obs)为路径点到最近障碍物点的欧式距离。

采用障碍物膨化的方法，实现上述约束，使Psparse出现在膨化后的障碍物边缘。障碍物膨胀公式如下：

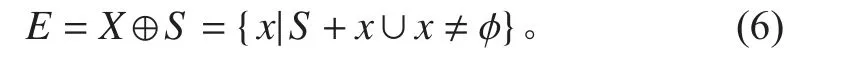
式中：X 为障碍物集合；x 为障碍物集合中的栅格元素；E 为输出结果；S 为膨胀结构元素，相关参数的选取如下式：

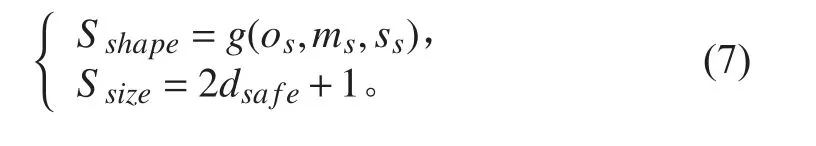
其中：Sshap为S 的形状；os为障碍物形状；ms为障碍物周边可行区域大小；ss为环境场景；g 为关系函数；Ssize为S 的尺寸；dsafe为安全距离。

选择不同大小与形状的膨胀结构元素，会改变路径关键点的位置，从而对路径长度与路径拐角的大小造成影响，如图5 所示。图像大小为300*300 像素，图像中心处有一个半径15 像素的圆形障碍物。

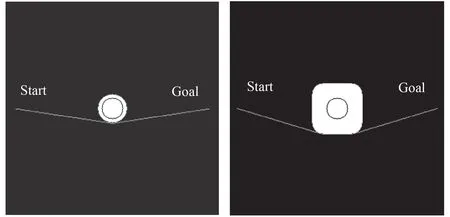
图 5 圆形小尺寸膨胀结构元素和方形膨胀结构元素Fig.5 Round small size and square big size

图5 左图是基于Sshap=circle，Ssize=11 的膨胀结构元素的路径规划示意图，其中环形区域为dsafe=5 的量化安全距离区域。

图5 右图是基于Sshap=square，Ssize=41 的膨胀结构元素的路径规划示意图，其中外圈区域为dsafe=20 的量化安全距离区域。

通过图5 的对比，可以看出，Ssize决定了dsafe的大小；Sshap影响着路径拐角的大小。

在加入了安全距离约束后，每一个路径点都会满足 d(c ,obs)≥dsafe，且 d(Psparse,obs)=dsafe，因此对安全距离进行了量化，从而能够规划出一条满足安全距离的最短路径。

2.4 无人艇运动学约束

现有的路径规划算法，往往把无人艇看作一个理想点，没有考虑到无人艇的运动性能。实际航行中，当无人艇以稳定速度转弯时，为了防止无人艇翻船，存在一个最小转弯半径Rm。当规划出的路径拐角较小时，无人艇无法跟踪此路径。

因此传统方法会对每一个路径拐点进行判断。当拐角为锐角时，进行拐角优化处理。如图6 所示。利用半径为Rm的圆弧对路径点A 前后的路径进行拟合,从而得到切点B1、B2，原来的路径为 B1B2A可以拟合为，再对圆弧做切线，将得到 C1C2作为拐角优化后的路径来代替。

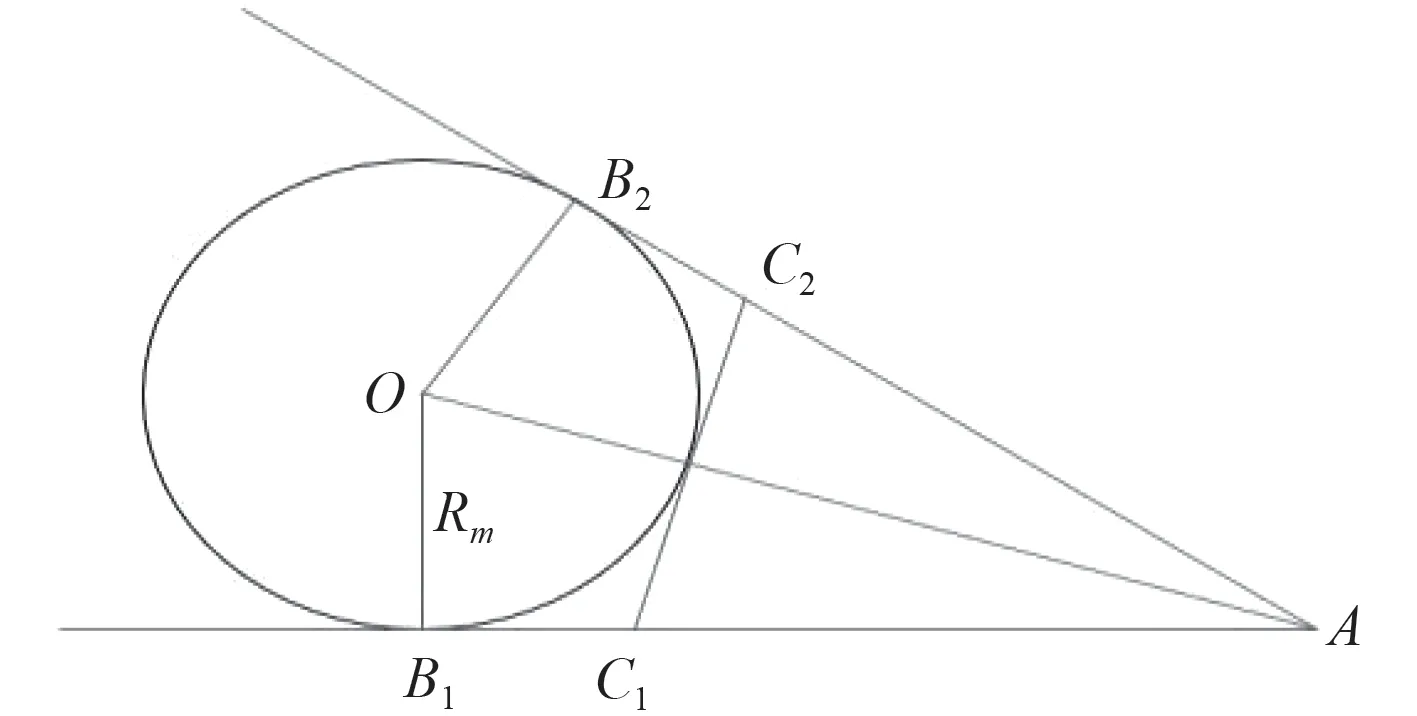
图 6 拐角约束Fig.6 Corner constraint diagram

由于本文对势场函数进行了改进，并加入稀疏点约束，路径关键节点将出现在障碍物边缘，如图7（a）所示。由于又加入了安全距离约束，最后会得到一条量化安全距离的最短路径，因此这条路径不会存在为锐角的拐角，如图7（b）所示。图7（b）中的障碍物由图7（a）中障碍物膨化得到，膨胀结构元素的形状为正方形，尺寸为3。

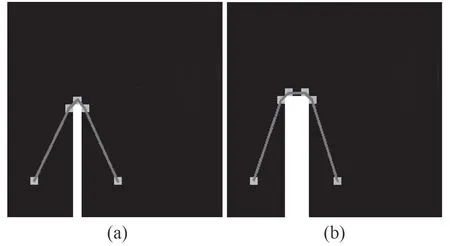
图 7 自动满足运动学约束示意图Fig.7 Automatically satisfying kinematic constraint

从图7 可以看出，加入了安全距离约束后，路径拐角将不会出现锐角。

2.5 海事规则约束

国际海上避碰规则公约（International Collision Regulations，COLREGS）是由国际海事组织制定，为了防止、避免海事船舶相撞而制定的海上交通规则[14]。为了无人艇的航行安全，应使无人艇遵守国际海上避碰规则公约。

根据COLREGS、船舶避碰的经验数据以及实际船只在复杂海洋环境中航行范围，为无人艇定义了追赶（Overtaking，OT）、相遇（Head-on，HO）、右交叉（Crossing from right，CFR）、左交叉（Crossing from left，CFL）4 种冲突局面，并可得到冲突局面的关系函数和航行规则表。

式中：P 为目标船只所在范围，如图8 所示。 Δθ为无人艇与目标船只航向角角度差，并将无人艇的航向定义为0°，。

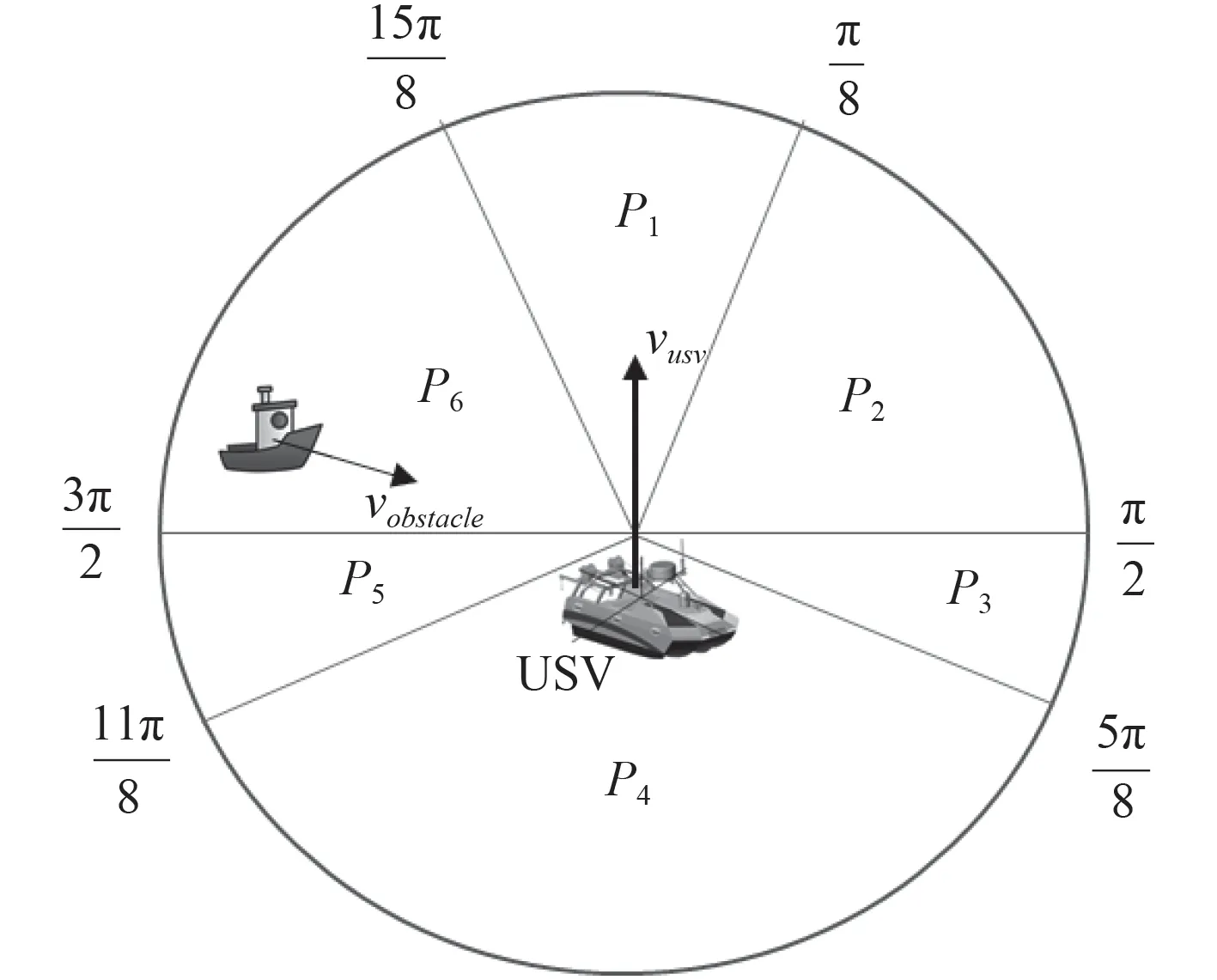
图 8 无人艇与目标船只相对位置图Fig.8 Relative position map of USV and target vessel

根据COLREGS 可以得到无人艇在遇到目标船只的避碰转向模型：

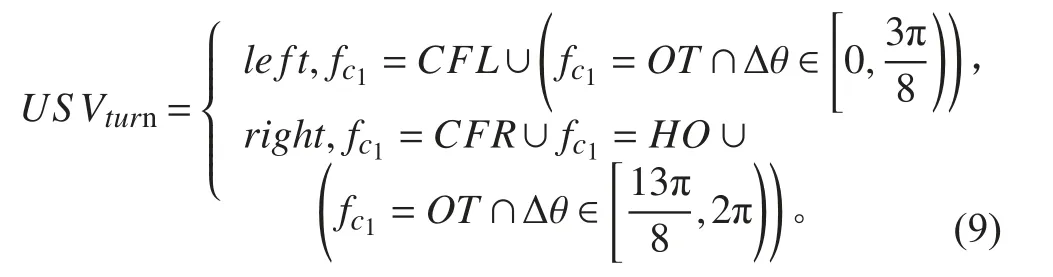
由于改进迭代势场法在加入了安全距离约束后，可以通过量化安全距离，沿膨化后障碍物边缘通行。因此可以通过环境感知系统检测目标船只的位置，再利用HMM 的方法预测目标船只的位置，根据表1 和式（9），判断将向哪个方向转向。然后对障碍物进行选择性膨胀，从而满足海上避障规则公约的要求，如图9 所示。

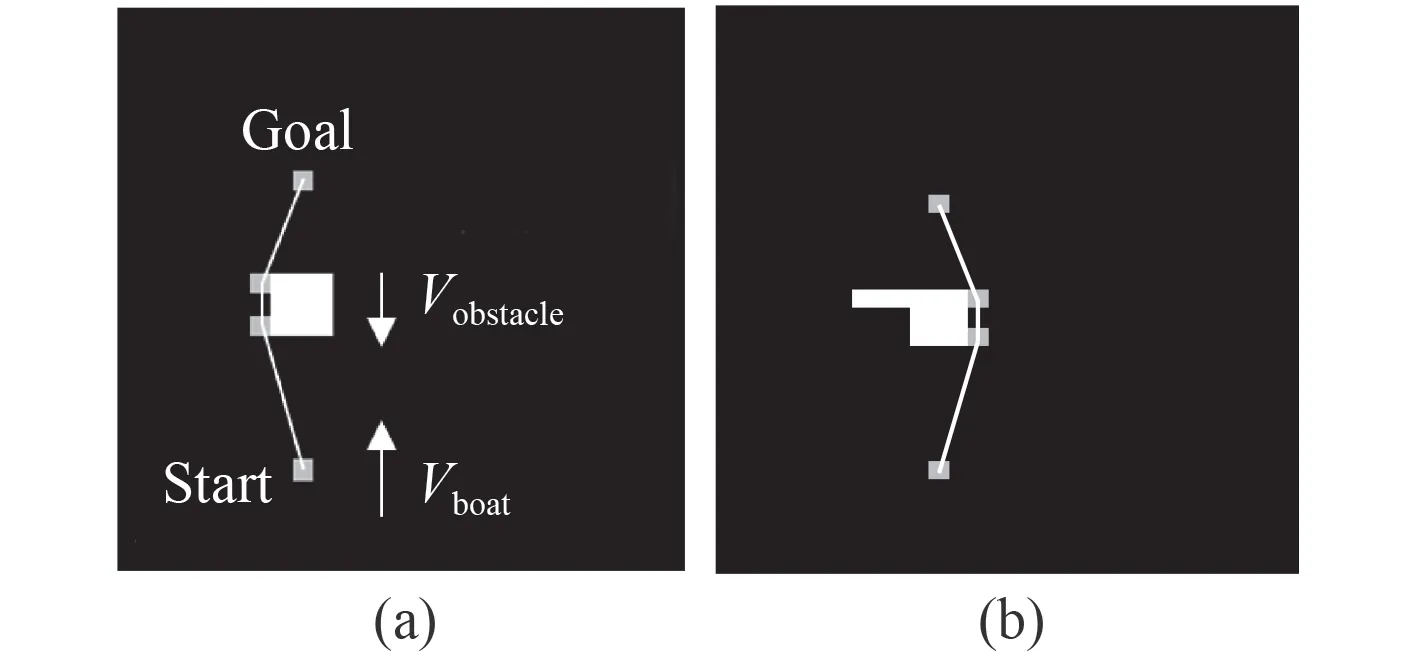
图 9 海事规则约束下的无人艇避障方向Fig.9 Obstacle avoidance direction under the COLREGS

图9 （a）表示在不加入海事规则约束下的无人艇动态避碰路线。由于此时无人艇会进入HO 局面，按照式（9）和表1 可知，无人艇应向右绕行。为了确保符合COLREGS，在障碍物中沿绕行方向的反方向进行选择性膨胀，如图11（b）所示。由于Psparse是能够构成最短路径的最优点，针对图11（b）中的非对称障碍物，将会规划出向右绕行的路径。

改进迭代势场算法流程如见图10 所示。

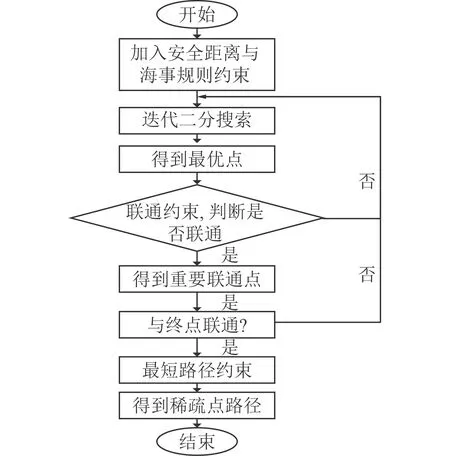
图 10 改进迭代势场法流程图Fig.10 Improved iterative potential field method flow chart

3 仿真试验

3.1 算法性能仿真

由于无人艇航行实际场景中的障碍物分布往往较为简单与单一，为了能够清楚显示本文算法的优点，采用如图11 所示的复杂迷宫环境来验证稀疏迭代算法的性能和有效性，并与传统迭代势场算法进行对比分析。其中图像大小为300*300 像素。

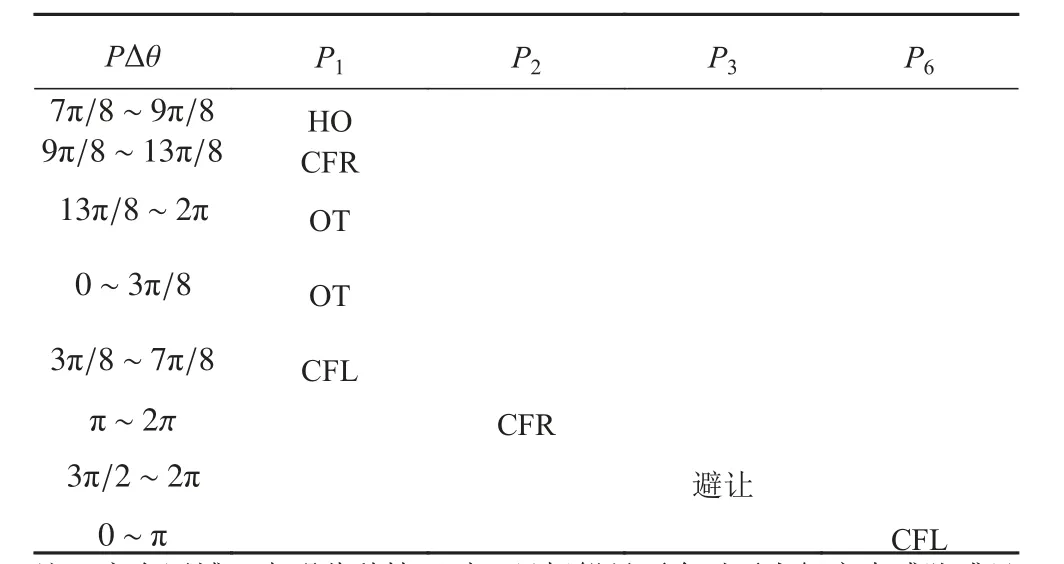
表 1 航行规则表Tab.1 Navigation rules table

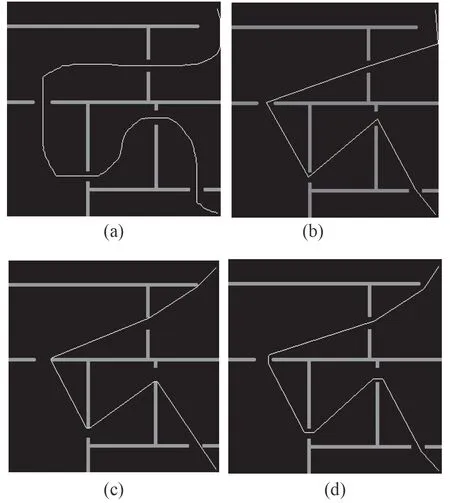
图 11 迭代势场与改进迭代势场法的路径规划图Fig.11 Path planning with IPF and SIPF

图11（a）和图11（b）为传统迭代势场算法规划出来的路径，势场函数参数a=1，b=1。

图11（b）是在传统迭代势场算法的基础上加入最短路径约束所规划出来的路径。

图11（c）和图11（d）为稀疏势场算法规划出来的路径，其中的势场函数参数。

图11（c）为稀疏迭代势场算法（没有加入安全距离约束）规划出来的路径。图11（d）为稀疏迭代势场算法（安全距离为4 个像素，膨胀结构元素形状为正方形）规划出来的路径。

规划出来的路径相关参数见表2。其中time 为算法运行时间，lenth 为路径长度，dist 为平均障碍物距离，即

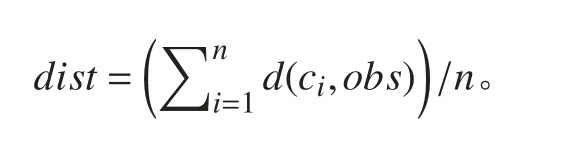
表 2 迭代势场法与稀疏迭代势场法的迷宫地图试验数据Tab.2 Related data of IPF and SIPF on maze map

式中：n 为路径点个数， d(ci,obs)为每一个路径点到离自己最近阻碍点的距离。Uobs(c)

从图11（a）和表2 可以看出，由于考虑 ，迭代势场算法规划出的路径整体较为平滑，但无法量化安全距离，且计算时间较长，不满足局部避碰的实时性要求。

从图11（b）中可以看出，即使加入了最短路径约束，迭代势场算法规划出来的路径依然不是最短路径，这是由于 Uobs(c)项影响了路径最优点的生成位置。因此认为迭代势场算法不具备快速避碰功能。

从图11（c）与图11（d）以及表2 可以看出，稀疏迭代势场算法在加入了安全距离约束后可以规划出一条量化了安全距离的最短路径，符合快速避碰的需求。

综上，我们可以看出稀疏迭代势场算法的平均运行效率比传统迭代势场算法提高了14.4 倍，此外能够量化安全距离，得到最短路径，满足海事规则和运动学约束，能够让无人艇实现实时、快速、动态地安全避碰。

3.2 无人艇静态障碍物避碰仿真

设初始运动参数如下：航速v = 5 m/s，航向θ=90°，无人艇航向坐标系见图8，终点的方位为90°，距离无人艇280 m。静态障碍物是一个半径15 m的圆形障碍物，方位为90°，距离无人艇125 m。其中地图大小为300*300 像素。

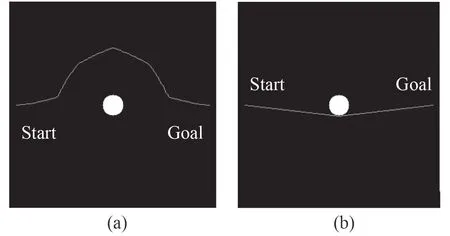
图 12 静态障碍物避碰径示意图Fig.12 Static obstacle avoidance diagram

图12 （a）为迭代势场算法规划出来的路径，势场函数参数 a= 1， b= 1。

图12（b）为稀疏迭代势场算法（没有加入安全距离约束）规划出来的路径，规划出来的路径相关参数见表3，表中参数含义与表2 相同。

从表3 可以看出，稀疏迭代势场算法的路径规划时间比迭代势场算法小了一个数量级。从图12（b），图5 可以看出，稀疏迭代势场算法规划出来的路径是最短路径，且不存在有锐角的拐角，满足无人艇的运动学约束。当dsafe增大时，lenth，dist 也会随之增大。表明稀疏迭代势场算法可以很好地规划出一条量化了安全距离的最短路径。此外平均规划效率比传统迭代势场法提高了16.6 倍。

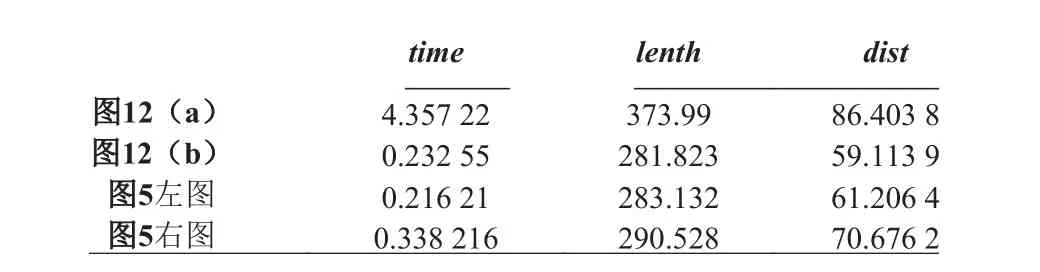
表 3 采用迭代势场法与稀疏迭代势场法进行静态障碍物避障得到的相关数据Tab.3 Related data of static obstacle avoidance using IPF and SIPF

3.3 无人艇动态障碍物避碰仿真

设本艇初始运动参数如下：航速v=5 m/s，航向θ=90°，无人艇航向坐标系见图8，终点的方位为90°，距离无人艇280 m。动态障碍物是一个半径15 m的圆形障碍物，其中地图大小为300*300 像素。

动态障碍物以3 m/s 的速度向东航行，且 Δθ=0°，基于HMM 方法，预测动态障碍物距离无人艇125 m，在无人艇90°方向。根据表1 和式（9），可知无人艇与目标船只处于OT 局面，无人艇应向左绕行。为此采取图13 所示的选择性膨胀方法，确保无人艇避碰符合海事规则约束。

图 13 OT 局面下无人艇动态航迹Fig.13 USV dynamic track under OT situation

4 实船验证

针对算法开展实船试验。基于海图和航海雷达获知全局地图，并使用稀疏迭代势场法进行全局路径试验。基于航海雷达、激光雷达、声呐、摄像机等传感器获知局部环境信息，并基于稀疏迭代势场法进行局部路径规划，局部路径规划的感知距离为600 m。在距离障碍物100 m 时开始进行避障，量化安全距离为25 m。

图 14 全局路径规划径示意图Fig.14 Static obstacle avoidance diagram

全局路径规划图如图14 所示。其中无人艇以12 kn速度航行，航向为45°，目标船只以5 kn 速度航行，航向为90°，无人艇航向坐标系见图8。

由于目标船只近似为矩形且周边只有一个障碍物，采用正方形结构算子进行膨化以满足安全距离约束。可以看出，该方法能够规划出一条安全、符合C O L R E G S、无人艇运动学约束的最短路径。在600*600 像素的地图上能够以2 Hz 的频率进行规划，满足无人艇局部避碰的实时性要求。

5 结 语

本文针对无人水面艇的局部避碰进行了研究，所提出的稀疏迭代势场算法不但避免了传统人工势场法所产生的局部极小值问题，还解决了栅格法规划的路径无法满足无人艇运动约束的问题，而且可以实现实时、快速、安全地避碰，并且规划出来的路径符合无人艇的运动特性和海事规则。最终能够在多约束条件下，规划得到一条量化了安全距离的最短路径，让无人艇具备自适应场景功能。仿真分析和实船试验均验证了本文所提方法的有效性。且表明稀疏迭代势场法的运行效率比迭代势场算法提高了14 倍。