基于无源回波模型的分布式孔径雷达压缩感知成像方法

王 洁, 盛佳恋, 付朝伟, 王海涛, 徐逸宇

(1.上海无线电设备研究所,上海201109;2.上海目标识别与环境感知工程技术研究中心,上海201109)

0 引言

无源雷达具有“四抗”优势,在战争中生存能力较强[1-4]。目标截面积不会对无源雷达的作用距离产生影响,因此,无源雷达有良好的信号适应能力和抗干扰能力[5]。随着现代社会的进步,外部机会发射源(Illuminators of Opportunity,简称IO)数目急剧增加,为基于外部发射源的无源雷达的发展和应用提供了更好的硬件基础,利用外部发射源的无源雷达成像技术将在城市及周边区域监控、室内监控等城市安全防御中有良好的应用前景。

现有大多数无源成像方法普遍需要设置辅助通道或专用接收机,以接收来自发射源的直达波信号。本文借鉴Yazici等人提出的适用于复杂环境的接收机设计思路[6],研究无需发射源信息的无源分布式雷达的成像方法。已有研究可以实现对不同观测背景、不同收发配置下的无源雷达静止目标和运动目标的成像[7-10]。该方法无需提供发射源信息,针对非合作目标情形有很大应用空间,优势明显,值得继续研究。由于观测场景中动目标个数有限,满足稀疏特性,因此可以将压缩感知理论引入无源雷达成像方法的研究。

基于已经发展成熟的无源回波模型,本文能够用远小于奈奎斯特采样定律要求的样本数对信号进行重构,可以实现对运动目标位置和速度的估计。首先构建无源回波模型,参考信号是分布式接收孔径中任意一个接收单元接收到的信号,则该参考信号能用来描述其余各接收单元接收到的信号,因此,接收信号中去除了有关发射源的信息。然后,随机降采样接收信号,在压缩感知的基础上采用正交匹配追踪(Orthogonal Matching Pursuit,简称OMP)方法对目标位置和速度重建。此方法利用分布式接收孔径,配置灵活度高,应用压缩感知可大大降低运算量和硬件成本,仿真实验成果证明了此方法的有效性。

1 无源回波模型

电磁波在介质中的传播模型可描述成[11-13]:

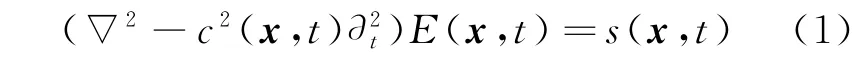
式中:s是关于辐射源的信息,包含辐射源位置,信号波形和辐射天线的方向性图;E是t时刻辐射源s在位置x形成的电场;c是电磁波在介质中的传播速度,可定义如下[14]:

式中:c0表示均匀背景介质里恒定电磁波的传输速度;qv表示t=0时刻目标在速度区间的分布函数。

电磁波在背景介质中的传输特性能够通过格林函数来表示:

其中,格林函数g描述了点状发射源在位置y发出的冲激信号于t时刻对位置x发出的电场。格林函数在自由空间主要描述了两个特征:一是电磁波从发射源传播到某点的时延;二是波传播过程中的能量衰减,能够表示为

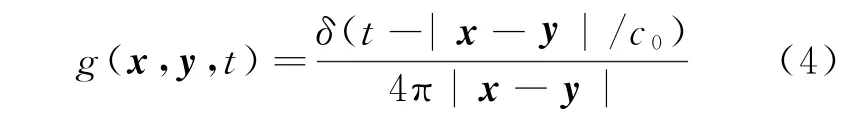
式中:|x-y|表示x和y之间的距离。

目标产生的散射场强度远低于入射场,因而运动目标产生的散射场能够描述为

式中:Ein(y,τ)表示入射场,数学表达形式为

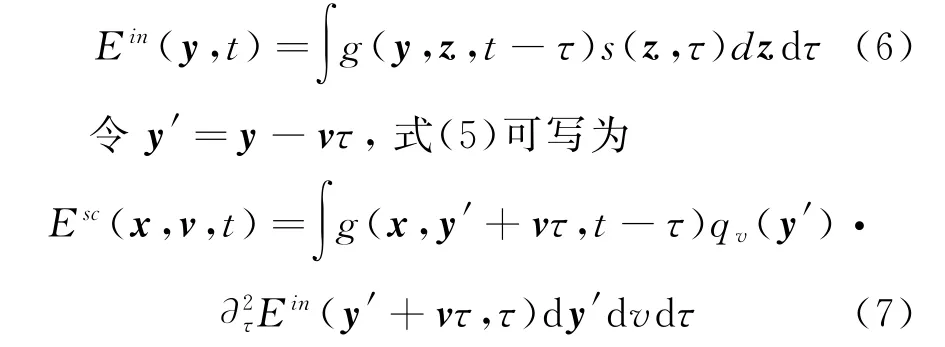
假设存在M部具有各向同性的发射机,发射源的数学表示形式可写为

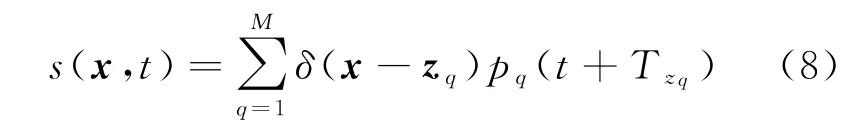
式中:zq,q=1,…,M为第q个发射机的位置,式(8)描述了t=-Tzq时刻发射机信号波形pq的叠加。

把式(8)带进式(7),运动目标产生的散射场可描述为

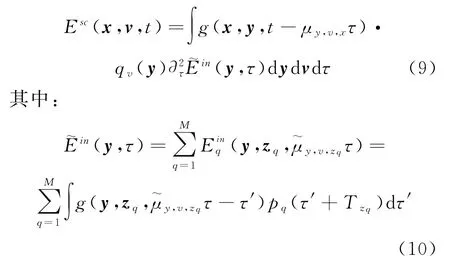
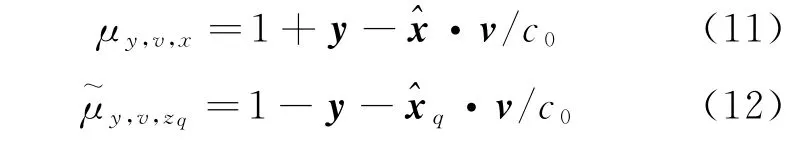
假设信道噪声是方差有限的零均值高斯分布,接收机噪声是n(t)。那么第i个接收机得到的回波信号能够表示为

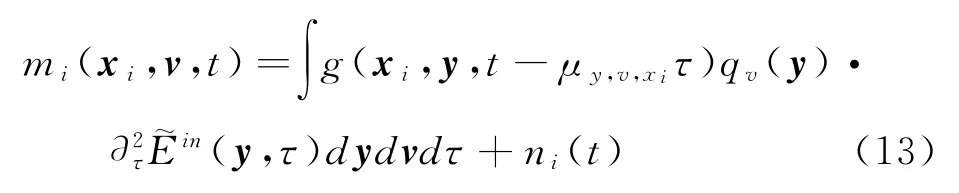
相应的式(13)的频域表达式为

本节将运动目标视作速度确定的点状目标,因此qv函数能看作确定值,其数学表示形式:

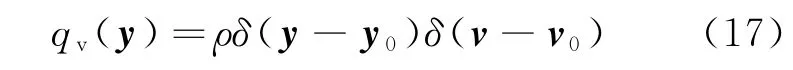
式中:ρ是y0处速度为v0的运动点目标的反射率。

由于发射源产生的电场被各个接收单元接收,所以参考信号能够表示为分布式孔径中的任意一个接收单元接收到的信号,剩余接收单元接收的信号可以用参考信号描述,即测量信号中去掉了关于发射源波形的信息。Py,v,i是前向传播算子,描述了信号由目标y处至接收机xi的传输,其数学表达式如下[15]:

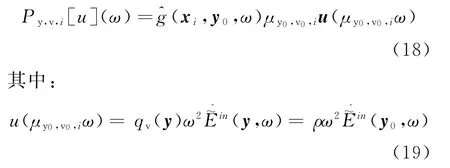
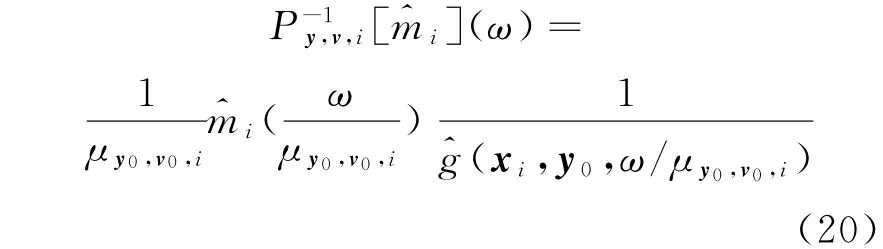
假定参考信号用接收单元xj处接收到的信号^mj(ω)来代替,则接收单元xi处接收到的信号^mi(ω)可描述成:

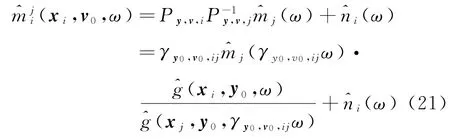
式中:γy,v,ij为由于目标运动,对xi和xj处接收机测量值产生的多普勒尺度因子的比值。它的表示形式为

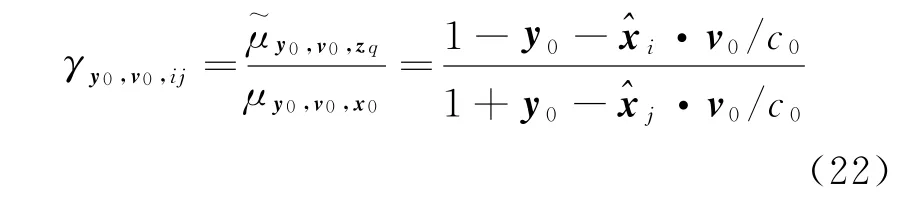
信号模型可以描述为xj处的参考接收单元信号后向传播至目标,接着从目标前向传播到接收单元xi。接收信号中没有发射源的波形信息,因此该信号模型可用于无源检测和成像。

2 压缩感知成像方法

利用CS的无源雷达成像算法突破了Nyquist采样定理,即每个测量值是传统理论下样本信号的组合函数,一个测量值就包含了所有样本信号的少量信息。因此,本文使用压缩感知方法可以保证良好的成像分辨率和较强的稳定性。

压缩感知理论表明,如果长度是P的某信号s具有W项稀疏的特性(s中非零值数目有W个,W＜＜P),那么通过一个Q×P维(Q＜P)的传感矩阵Φ得到的测量向量ψ会包括s的所有信息[17]:

压缩感知的传感矩阵与稀疏基需要满足不相关的条件,也就是具有有限等距性质(Restricted Isometry Property,简称RIP)[18]:

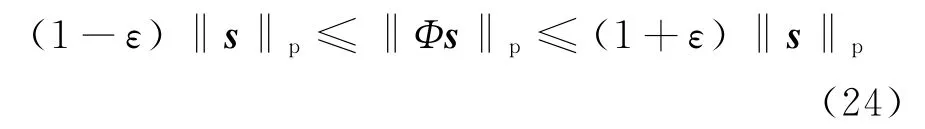
目标的几何形状决定了由散射点构成的图像,由于目标形状不具有规律性,图像的稀疏基s是随机产生的,因此能保证它与传感矩阵无相关性。

由于Q×P维测量矩阵Φ行数少于列数,式(23)是欠定方程,直接由测量向量ψ对初始信号s求解会获得无限多个解,压缩感知理论指出,若式(23)满足稀疏约束条件,那么就可以利用l0或l1范数意义下的优化问题以较高的概率从观测结果ψ中恢复原信号s,恢复过程用公式表示为

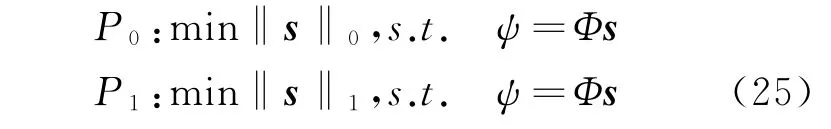
利用压缩感知理论进行信号重建的算法主要包括四类:贪婪算法、凸优化算法、统计优化算法和组合算法。贪婪算法因为计算速率较快而获得大量使用,本节主要利用贪婪算法中的正交匹配追踪算法。

2.1 测量向量模型和感知矩阵构造

为了获得观测向量ψ,将所有由K个测量值组成的N个接收单元的接收信号mn=[mn[1],mn[2],…,mn[K]]T向量化为NK×1维的观测向量:

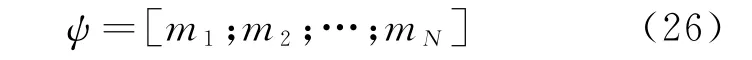
对运动目标位置进行估计时,将探测区域离散化为Nx×Ny个单元,其中水平方向Nx个单元,竖直方向Ny个单元,相应可以得到与每个探测位置相对应的长度为NxNy×1的运动目标位置状态向量sp。对运动目标速度进行估计时,将探测区域离散化为Nvx×Nvy个单元,其中水平方向Nvx个单元,竖直方向Nvy个单元,相应可以得到与每个探测速度相对应的长度为NvxNvy×1的运动目标速度状态向量sv。通常,探测区域内的运动目标个数远小于场景离散化后的单元数,目标状态向量具有稀疏特性。

对运动目标进行定位及速度估计时,运动目标的状态向量不同,因此对应的感知矩阵也不同。对于本节所讨论无源分布式孔径雷达成像问题,可利用式(21)所描述的信号模型来构成传感矩阵Φ。

估计运动目标的位置时,目标速度v已知,目标状态向量是位置状态向量sp。感知矩阵Φ∈CNK×length(sp)由所有接收单元的感知矩阵Φi∈CK×Length(sp)垂直排列得到。令φi,y表示第i个接收单元感知矩阵Φi的一列,对应于第i个接收单元在发射源位置y处的感知向量,其表达式为

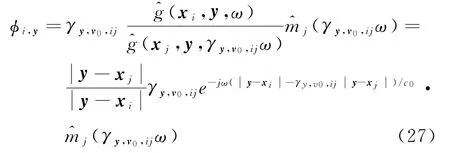
估计运动目标的速度时,目标位置y0已知,目标状态向量是速度状态向量sv。感知矩阵Φ∈CNK×length(sv)是由所有接收单元的感知矩阵Φi∈CK×Length(sv)垂直排列得到。令φi,v表示第i个接收单元感知矩阵Φi的一列,对应第i个接收单元在发射源速度v的感知向量,其表达式为

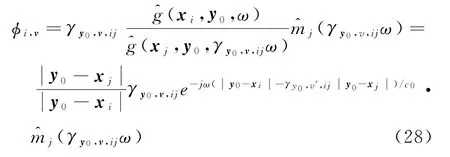
2.2 位置和速度重建算法

本节采用正交匹配追踪方法估计目标位置和速度。估计运动目标位置时,目标状态向量为运动目标位置状态向量sp,感知矩阵为相应的位置感知矩阵,估计运动目标速度时,目标状态向量为运动目标速度状态向量sv,感知矩阵为相应的速度感知矩阵。位置和速度重建的主要步骤:

a)初始化:令初始状态向量为零,即^s=0(估计目标位置时,状态向量s为sp;估计目标速度时,状态向量s为sv)。初始残差为测量向量r0=ψ。令循环标识s=0,索引集∧0为空集。设置稀疏度S,即目标状态向量中非零项数目。

b)更新s←s+1;

c)选取相应列:从相应感知矩阵Φ中选择一个和残差rs-1相关性最大的列,即:

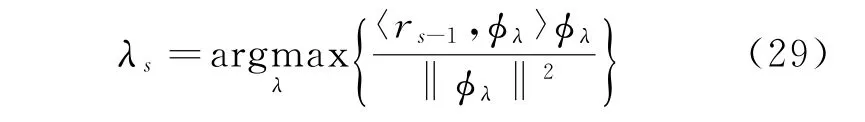
式中:φλ为感知矩阵Φ的第λ列,即λs←argmax{};

d)更新索引集合∧s=∧s-1∪{λs};

e)更新感知矩阵列Φs=[Φs-1φλs];

g)更新残差rs←ψ-;

h)判断是否满足s＞S,若是则终止,否则返回步骤(2)。

OMP算法最多需要S次循环即可收敛,最终得到的^sS即为重建的目标状态向量。OMP算法的另一种收敛准则是通过判断残差的能量,重复上述迭代步骤,直到残差能量与测量向量能量之比收敛到某一特定阈值,停止迭代,反之,继续迭代。

3 仿真与分析

为证明成像算法的有效性,并对上文提出的应用压缩感知理论的无源分布式孔径雷达成像方法进行检验,本节采用WiMAX信号对该成像方法进行检验。

WiMAX信号具有较大带宽,传输距离远,可用作无源雷达的发射源。WiMAX是在IEEE 802.16标准的基础上研发的宽带无线城域网技术,并且渐渐成为主要的无线宽带接入技术,一个基站的传播距离能达到50 km,信号带宽能达到20 MHz,因而基于WiMAX信号的无源雷达能够保证的最小距离向分辨率为7.5 m,并且可进行长距离检测,上述优点吸引了雷达界的大量关注[19-22]。

本节利用基于正交频分复用(Orthogonal Frequency Division Multiplexing,简称 OFDM)调制的Wi MAX信号进行仿真,带宽20 MHz,载频6 GHz,成像累计时0.13 s。单基情况下,理论可提供的距离向分辨率是7.5 m,速度向分辨率是0.42 m/s。仿真中考虑自由空间,暂不考虑杂波,假设噪声为高斯白噪声。

假定位置空间成像区域3 000 m×3 000 m,像素大小10 m×10 m,即成像区域包含301×301个像素单元;速度空间成像区域为[-20,20]m/s×[-20,20]m/s,像素大小0.2 m/s×0.2 m/s,即成像区域包含201×201个像素单元。发射机和接收机均放置在同一个水平面。假设一部发射机的位置是[2 200,3 000]m,两个运动目标的位置分别是[450,2 250],[1 500,1 500]m,速度分别为[-10,15],[12,-10]m/s。考虑两种接收机配置:

a)场景中有5部接收机,接收机位置分别为[0,0],[0,1 500],[0,3 000],[1 500,0],[1 500,3000]m;

b)场景中有8部接收机,接收机位置分别为[0,0],[0,1 000],[0,2 000],[0,3 000],[1 000,0],[1 000,3 000],[2 000,0],[2 000,3 000]m。

场景配置如图1所示。运动目标的位置空间配置如图1(a)所示,圆点代表运动目标的位置,箭头代表目标的运动方向,叉号代表发射机位置,菱形代表配置(1)中5部接收机位置,矩形表示配置(2)中8部接收机的位置。运动目标的速度空间配置如图1(b)所示,圆点代表目标的速度。

下面将针对上述两种场景配置进行仿真,并比较本节提出的利用压缩感知方法和文献[23]提出的利用广义似然比检验的成像方法。

3.1 压缩感知方法和基于广义似然比检验的成像方法的对比

针对上述两种场景配置,利用压缩感知方法和利用广义似然比检验的成像方法对运动目标的位置成像和速度成像结果如图2(a)至图5(b)所示。叉号代表发射机位置,菱形代表接收机位置,红色圆圈代表运动目标的真实位置。图2和图3描述了场景(1),利用5部接收机和1部发射机对自由空间中运动目标位置和速度的成像结果。图2(a)和图2(b)是采用压缩感知方法获得的位置和速度成像结果,图3(a)和图3(b)是采用广义似然比检验的成像方法得到的位置和速度成像结果。

由图可知,两种方法均可准确地对目标成像并估计目标速度。图2中目标位置和速度由峰值点,即亮度最高点的位置确定。红色圆圈表示目标的真实位置和速度,由图2可知,图像中最亮的两个点均在圆圈内,因此利用压缩感知成像方法可以准确的对运动目标进行成像和速度估计。

基于广义似然比检验的成像方法是几条双曲线束在目标位置或速度处相交,此外也将衍生出几条双曲线束不相交于目标处,它们的交点对成像产生干扰。图中红色圆圈为目标真实位置,由于双曲线交点在红色圆圈中,可以表明基于广义似然比检验的成像方法的正确性。

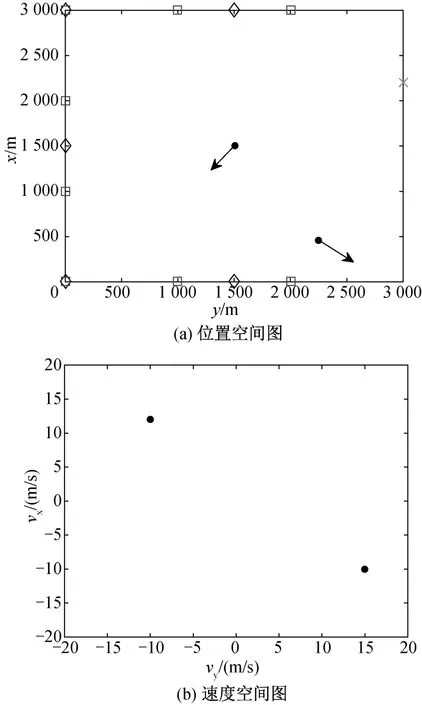
图1 自由空间中5/8部接收机,2个运动目标和1部发射机的配置图

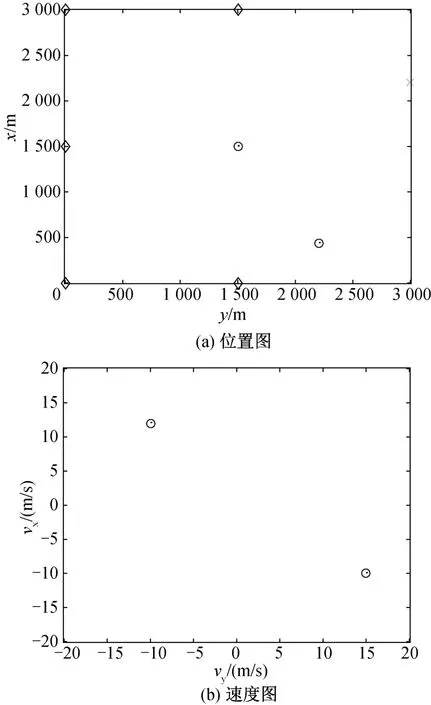
图2 自由空间中利用5部接收机、采用压缩感知方法对运动目标的成像结果

图4和图5描述了场景(2),利用8部接收机和1部发射机对自由空间里运动目标位置和速度的成像结果。图4(a)和图4(b)是采用压缩感知方法获得的位置和速度成像结果,图5(a)和图5(b)是采用广义似然比检验的成像方法得到的位置和速度成像结果。

表1给出了两种接收阵列配置下,采用CS方法和广义似然比检验方法对运动目标进行定位和速度估计时每个接收机的采样样本数。

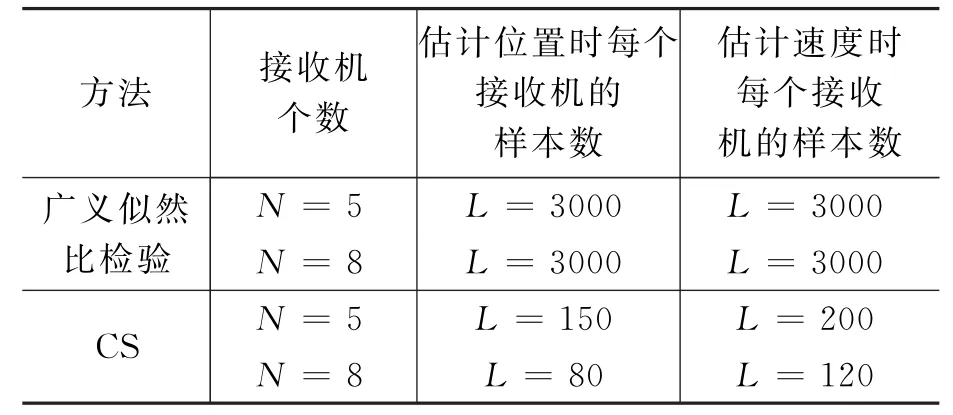
表1 运动目标位置和速度估计时每个接收机的采样样本数

对比两种方法可知,压缩感知方法可以用很少的样本数进行目标定位和速度估计。在不影响成像精度的情况下,增加接收机个数,利用CS方法进行目标定位和速度估计时所需的采样样本数可以进一步减少。当接收机个数增大时,图5(a)和图5(b)成像区域中的双曲线条数增多,因此运动目标处的光束亮度增强,但相交于非目标处的虚假点也增多。

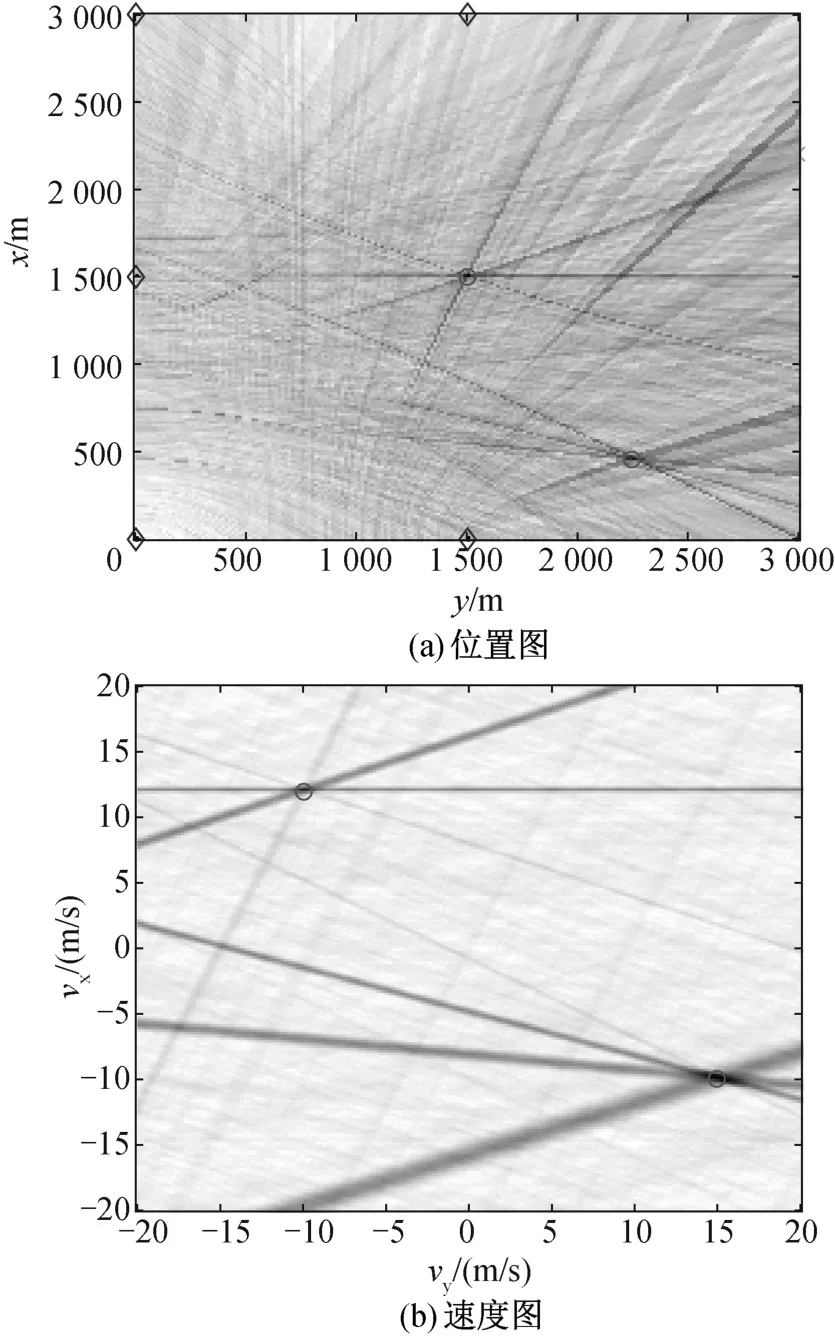
图3 自由空间中利用5部接收机、采用广义似然比检验方法对运动目标的成像结果

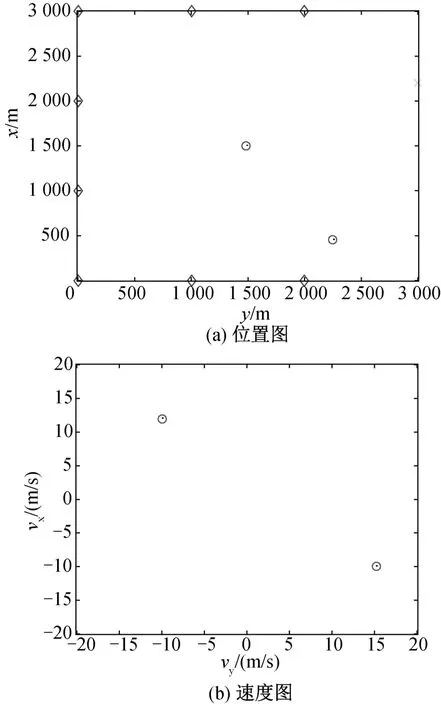
图4 自由空间中利用8部接收机、采用压缩感知方法对运动目标的成像结果

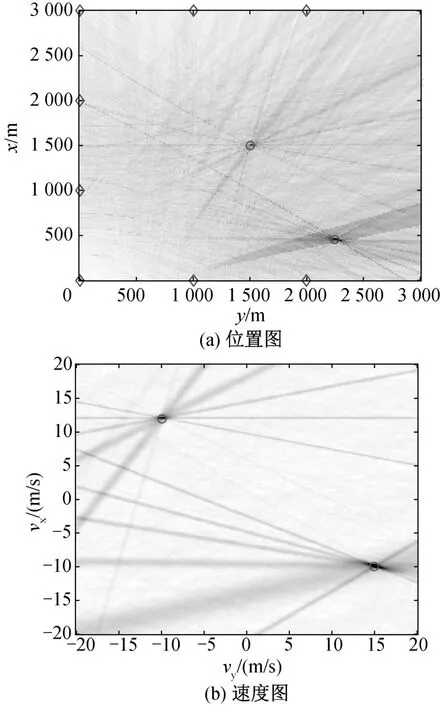
图5 自由空间中利用8部接收机、采用广义似然比检验方法对运动目标的成像结果

3.2 信噪比对压缩感知成像方法的影响

上述仿真是在无噪声情况下完成的,为了研究噪声情况下应用压缩感知方法对目标定位和速度估计的性能,在观测信号中添加高斯噪声。本节仿真实验,分别在信噪是10 d B,0dB和-10 dB条件下进行仿真。信噪比是信号功率与噪声的比值,数学表达式为:

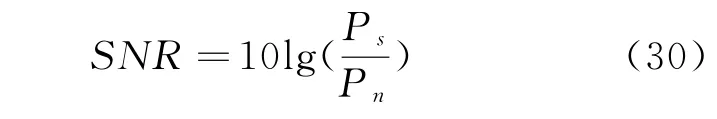
其中,Ps是接收信号功率,Pn是噪声功率。仿真时,将噪声干扰加入原始信号。在不同噪声环境下,对上文配置(2)位置和速度的成像结果如图 6所示。

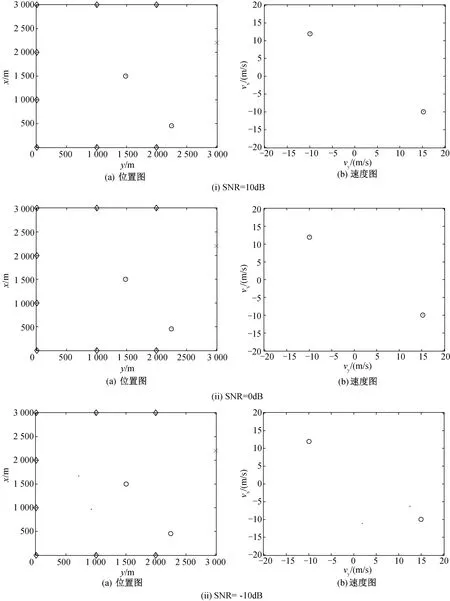
图6 不同信噪比情况下对位置和速度成像的结果

表2给出了不同信噪比时,对配置2采用CS方法进行位置估计和速度估计时每个接收机的采样样本数。

由图表可知,同一配置下对目标位置和速度进行估计时,所需的样本数量随着信噪比的升高而降低。由图6可知,信噪比是10 dB情况下,CS方法能够很好地重构出目标位置和速度;信噪比为0 dB时,虽然噪声对重构已产生影响,但通过增加采样样本数,仍然可以重构出正确的目标位置和速度;信噪比降为-10 dB时,由于噪声幅度过大,掩盖了真实的信号,尽管增加采样样本数量,CS方法也无法准确重建出目标位置和速度,影响重建质量。

仿真结果表明在低噪声情况下,本章应用压缩感知技术的方法能够在目标满足稀疏条件时精确重建目标位置和速度,并且能够减少采样样本数量。信噪比增大,所需的采样样本数减小。仿真结果表明了该算法的可行性。

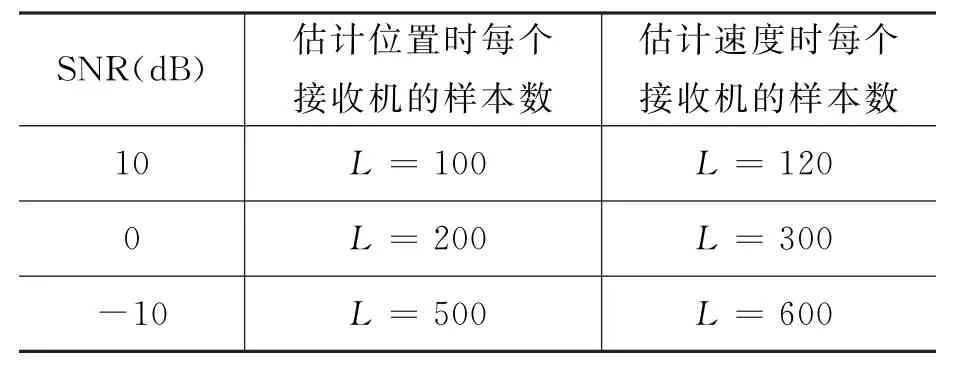
表2 不同信噪比情况下位置及速度估计时每个接收机的采样样本数

4 总结

针对自由空间中运动目标的定位及速度估计问题,本文提出了利用压缩感知技术和分布式孔径的定位方法。本文的测量模型不需要获取发射源波形信息,通过将一个接收单元信号作为参考,其余接收单元的信号就能够用此参考接收单元信号来表示。仿真实验结果证明,此定位方法获得的成像结果所受干扰少,并且可以明显减少采样样本数目。接收机个数增加时,采样样本数可以继续减少。此外,信噪比也会影响成像质量和采样样本的数量,随着信噪比增加,所需的采样样本数降低。