低信噪比下LFM-BPSK复合调制信号参数估计
2020-01-14孙富礼蒋张涛朱嘉颖
孙富礼, 蒋张涛, 沈 军, 朱嘉颖
(上海无线电设备研究所,上海201109)
0 引言
在现代电子战中,低截获概率(Low Probability of Intercept,LPI)雷达由于采用了大时宽大带宽的复杂调制信号以及进行功率管理等一系列技术手段,有效提高了雷达的战场生存能力,近年来得到了广泛应用。电子侦察接收机需要在没有先验信息的复杂电磁环境中截获敌方辐射源的信号,并对其进行特征分析、检测识别及参数估计,为后续的电子干扰和攻击等对抗措施提供基础。LFM-BPSK复合调制信号不仅具有LFM信号测距精度高和多普勒不敏感的特性,还具有BPSK信号多普勒分辨率及测速精度高的优点。已经广泛应用于多种雷达中[1]。因此,对LFMBPSK复合调制信号参数估计算法的研究具有重要的现实意义。
在已有的LFM-BPSK复合调制信号参数估计方法中,文献[2]首先利用时频曲线拟合法对LFM-BPSK信号进行识别,然后利用离散多项式相位变换法和多尺度小波变换法基于信号重构技术对LFM-BPSK复合调制信号进行参数估计;文献[3]提出了基于分数阶傅里叶变换和ZAM分布联合估计的参数估计算法,首先估计信号的起始频率和调频斜率,然后对解线调之后的信号提取ZAM分布在起始频率截面的负峰值估计码元宽度;文献[4]提出了在高斯噪声下伪码一线性调频复合信号参数估计的方法。文献[5]则对复合信号参数估计理论的性能进行了分析。但是这些方法都是在高信噪比下才能准确估计出LFMBPSK复合信号的参数。本文首先对LFMBPSK复合调制信号进行平方运算去除相位编码,将信号变换为LFM信号,为兼顾估计精度和信噪比门限,分段滤波后采用迭代插值分数阶傅里叶变换方法估计该LFM信号的起始频率和调频系数。在此基础上重构线性调频信号,并与复合信号共轭相乘得到基带BPSK信号,然后采用循环谱相关技术提取码速率。该方法能够有效提高低信噪比下信号参数估计的精确度和稳定性。
1 信号模型
LFM-BPSK信号可以表示为
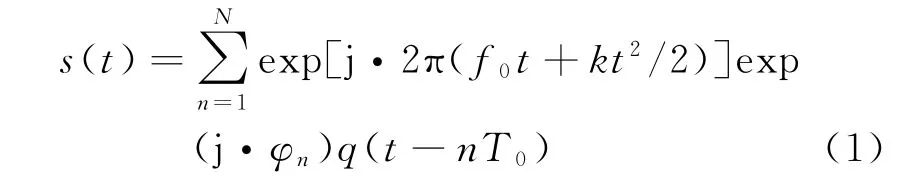
式中:q(t)=1;t∈[0,T0];f0为信号初始频率;B为信号带宽;k=B/T为调频斜率;T=NT0为信号时宽;q(t)为矩形信号;T0为码元时宽;φ0为二元序列,取0或π。
为直观地分析LFM-BPSK复合调制信号的特征,选取如下仿真参数:采样频率为fs=200 MHz,初始频率f0=5 MHz,码元宽度为τc=0.5μs,码元序列采用Barker码:101001110。此复合调制信号的时域波形图及频谱图如图1所示。
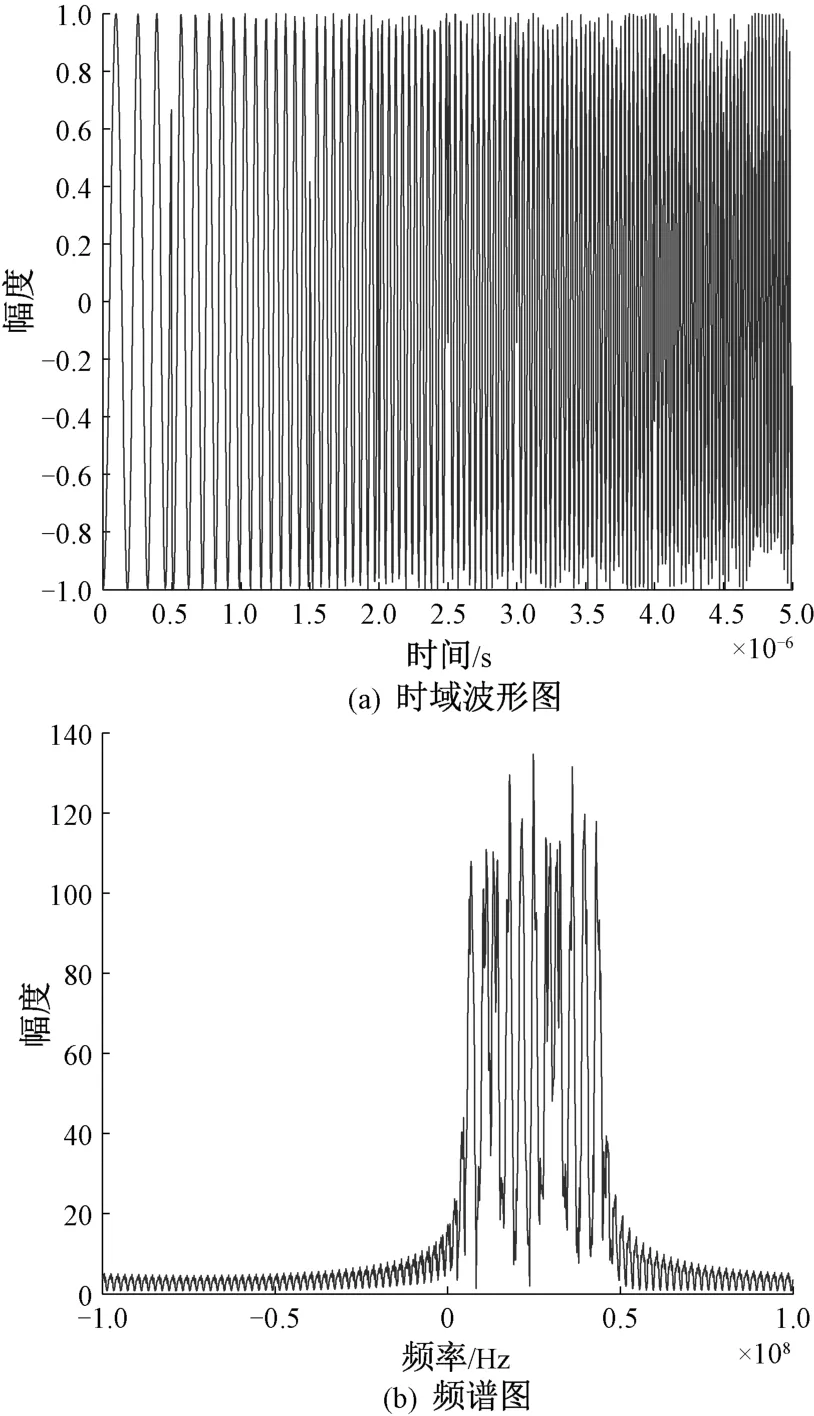
图1 LFM-BPSK复合调制信号的时域波形图及频谱图
由LFM-BPSK复合调制雷达信号的时域波形图和频谱图可以看到,其波形更加复杂,频谱的分布与线性调频信号类似但更加动荡。复合调制雷达信号是通过组合多种调制方式而形成的,能够融合多种信号的优点,弥补其各自不足之处。与单一调制类型信号相比,复合调制信号能够获得更大的时宽带宽积,具有更好的距离分辨率和速度分辨率,同时提升了低截获性能,加大了敌方侦察接收机截获和检测识别的难度,对传统雷达侦察接收机造成了严峻挑战。
2 参数估计
2.1 插值优化FRFT原理
FRFT是一种广义的傅立叶变换,其可以看作是信号在时频平面内任意旋转一定角度后在分数阶域的投影[6]。
信号x(t)的FRFT定义式为
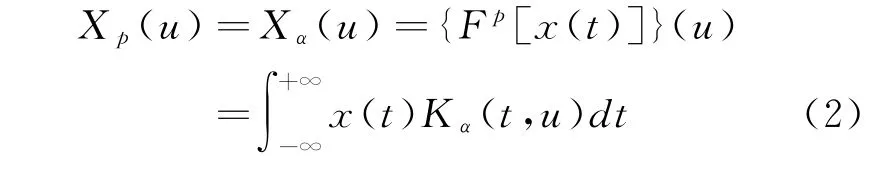
式中:p为FRFT的阶数;α=pπ/2表示旋转角度;Fp[·]为 FRFT 的算子符号,其核函数Kα(t,u)定义为
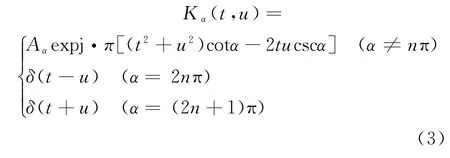
式中:Aα=为整数。
在实际应用中,文献[7]提出了一种分解型快速算法,该快速算法需要进行量纲归一化处理,将时域t转换为无量纲的域t/λ,将频域f转换为无量纲的域fλ,其中λ=。
量纲归一化使信号在时域和频域具有相同的长度L=。将式(2)改为如下形式:
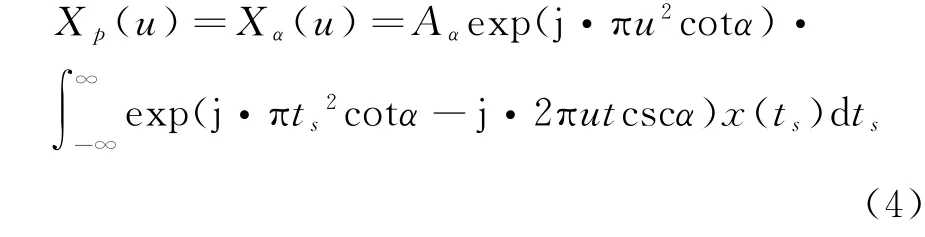
式中:ts=t/λ,分解型离散FRFT可以表示为
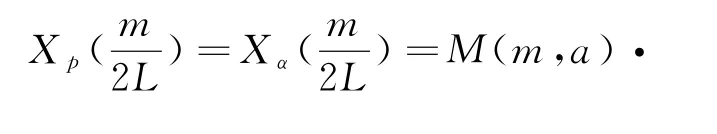
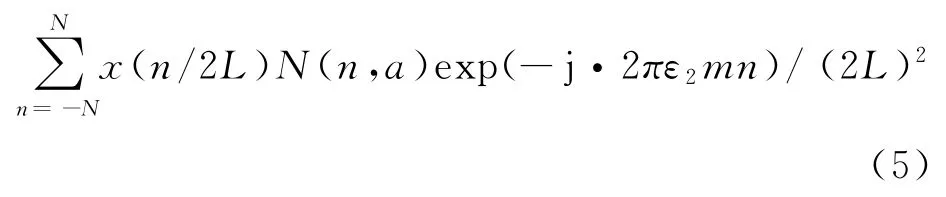
式中:M(m,a)=Aα/2L·exp(j·πε1m2)/(2L)2,N(n,a)=exp(j·πε1n2)/(2L)2。 其中:对信号进行了2倍内插,因此需要对最后结果Xα(m/2L)进行1/2倍抽取以得到离散采样Xα(m/L)。
由FRFT的定义可知,LFM信号将在分数阶域形成能量聚集谱,而高斯白噪声的能量将均匀分布在整个分数阶域。因此,线性调频信号的参数估计的基本思想是在(α,u)二维平面内搜索线性调频信号的能量聚集峰值点,得到峰值坐标(^α0,^u0),其中m为正整数。各参数估计结果为
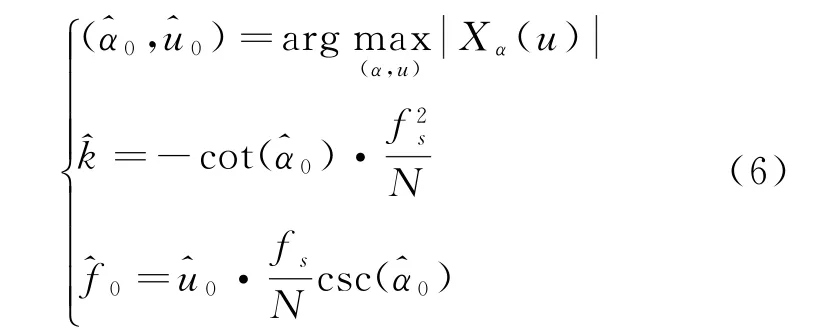
式中:fs为采样频率;angle[·]为取幅角。
线性调频信号的参数估计就是在离散化(α,u)二维平面上进行峰值搜索。由于噪声和离散(α,u)平面的分辨率造成了搜索到的峰值点与真实峰值点之间的偏差,称搜索得到的峰值点为准峰值点。
分数阶u域离散化造成的有限分辨率使得搜索得到的准峰值点与真实峰值点的偏差较大,进而影响到信号参数估计的精确度。而在α域可以通过设置更小的Δα来降低离散化处理带来的偏差,但是计算量会大大增加。因此,可以考虑通过提高u域离散化处理后的分辨率,解决α域分辨率与运算量之间的矛盾来提高参数估计的精度。
准峰值点的FRFT为
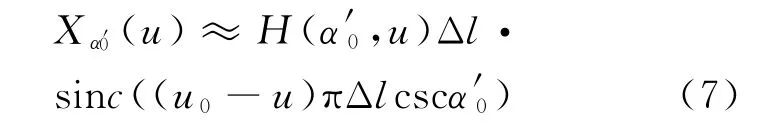
准峰值点在u域的取值为=uk=kΔl/N,由于u域离散化,真实峰值点u0的坐标应该在[(k-1)Δl/N,(k+1)Δl/N]内。基于上述分析,利用阶分数阶傅里叶变换的函数表达式对u进行插值补偿,以得到更精确的坐标。
则有ψ1=ψ0+πcscα'0,ψ2=ψ0-πcscα'0。由之前分析知 (u0-uk)πΔl≤π/2。因此,ψ0∈[-π/2,0],ψ1∈ [π/2,π],ψ2∈ [-3π/2,-π]。根据上述求解得
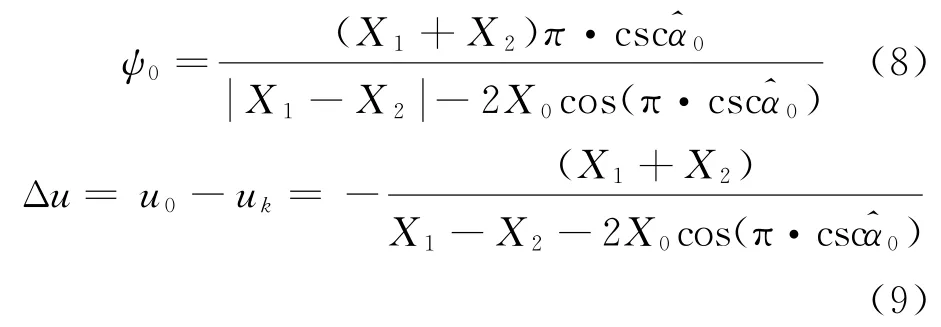
综上所述,插值补偿后得到的更加精确的峰值点在u域的坐标为
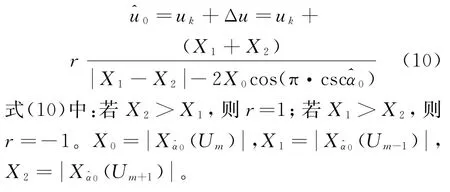
利用插值补偿后的^u0进行参数估计,可以有效提高线性调频信号的幅度、初始频率和初始频率的估计精度,由于离散化处理及环境噪声的影响,对信号相位信息的估计偏差较大。在现代雷达中,雷达信号频率较高,带宽较大,通常我们只关注信号的初始频率和调频斜率信息。偏差分析可知,当α的搜索步长Δα缩小到10-4时,由α域离散化造成的影响可忽略不计,但是这样会造成计算量的急剧增加,因此,可以考虑在适当的搜索步长下,对旋转角度α也进行插值补偿以降低峰值搜索准峰值点与真实峰值点的偏差,提高信号参数估计的精确度。
理论上,若α域的分辨率Δα取值足够小,那么搜索的准峰值点坐标就可以无限接近真实值,但是会产生巨大的运算量。若保证线性调频信号能够在u域产生突出谱线的条件下,可以设置较大的搜索步长,对旋转角度α也进行插值补偿的方法,得到的α0的精确估计^α0,可以有效降低运算量。
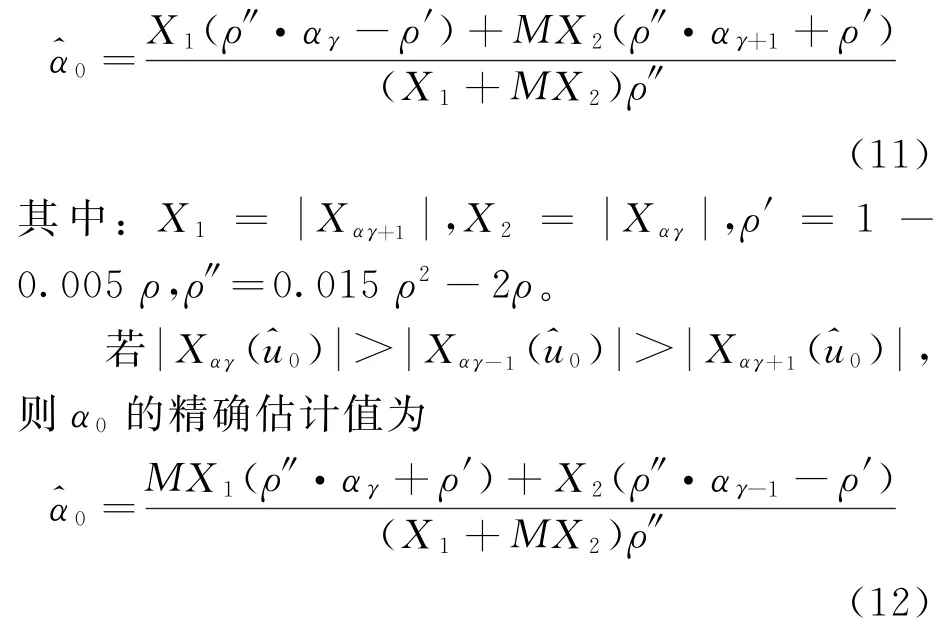
其 中:X1=,ρ'=1-0.005ρ,ρ″=0.015ρ2-2ρ。
因此,通过插值补偿法可以由准峰值点αγ和邻近准峰值点αγ±1得到峰值点α0的精确估计值。将其代入式(6)可得到精确估计的信号各参数。
2.2 循环谱相关
假设x(t)为循环平稳信号,则其相关函数可以表示为

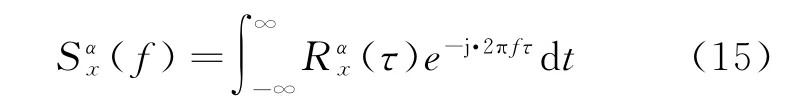
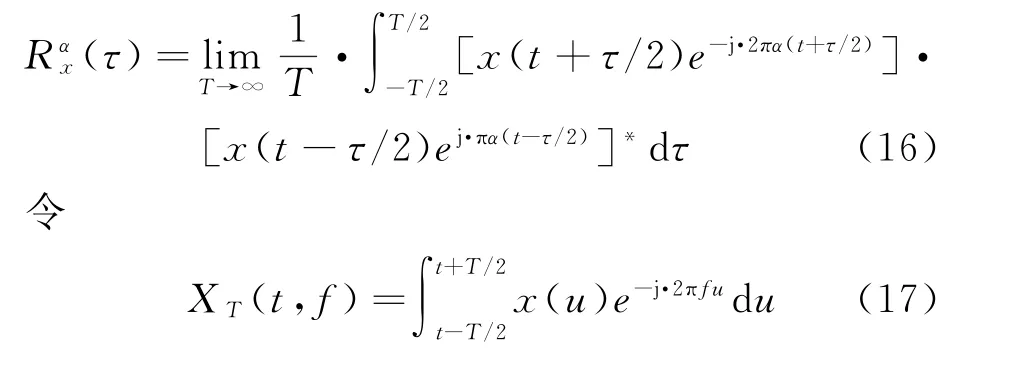
则有
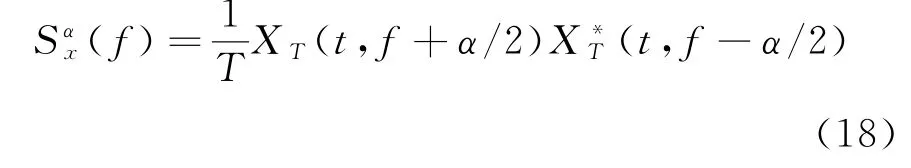
现实中,只能通过在一定的时间内采集有限的数据,通常用离散时域或频域平滑周期图法来计算信号的循环谱相关密度函数。由于雷达信号通常频率较高,在时域进行分析误差较大,因此本文采用离散频域平滑方法,其表达式为
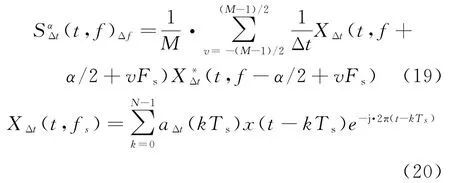
式中:Δf=MFs为频域平滑窗函数;Fs=1/(NTs)是频域采样宽度;Ts是时域采样宽度;aΔt为时间窗函数;Δt=(N-1)/Ts是数据总长度;N是Δt时间内的采样点数。
BPSK信号可以表示为
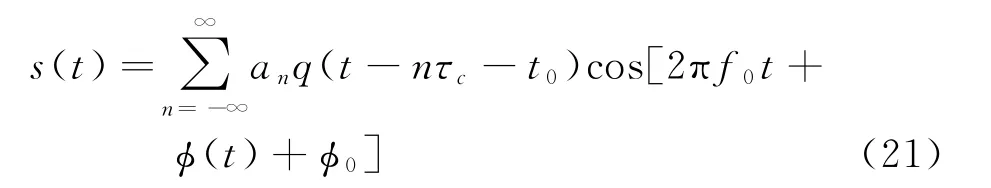
式中:{an}为独立同分布序列,等概率取1和-1。
因此BPSK信号的循环自相关函数为
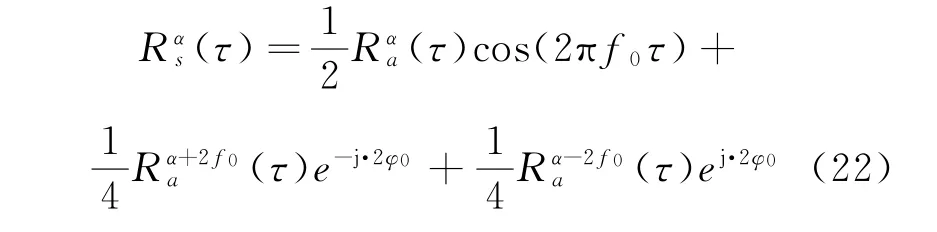

式中:k为整数;Q(f)为q(t)的傅里叶变换,BPSK信号s(t)的循环谱密度函数为
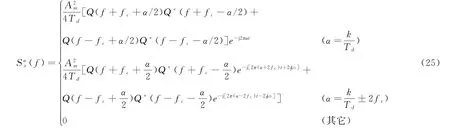
式中:Q(f)是BPSK信号q(t)的傅里叶变换;Td=1/fd为码元时宽;fc为信号载波频率;k为整数,为便于进行分析可令f=0,得出调制信号特征谱(0),可知其绝对值:
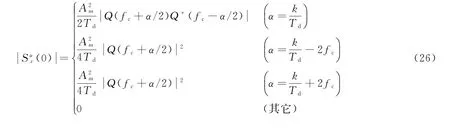
由式(26)可以看出,BPSK信号的载波频率、码速率和幅度决定了循环谱相关的绝对值。分析Q(f)可知,f=0时取最大值,f>0和f<0时逐渐减小。信号特征谱的模值在k=0,α=±2fc时取最大值,在k=0,α=±2fc+1/Td时,取次大值。而且信号循环谱相关的对称性,可以通过搜索在α>0时特征谱的模值的峰值对应的频率来估计二相编码信号的载波频率,二相编码信号的码元速率的估计则可以根据峰值与相邻的幅度次峰所对应的频差来实现。
2.3 参数估计步骤
为了提高LFM-BPSK复合调制信号参数估计算法的精度,需要先对信号进行分段滤波,相位编码信号对载波的相位进行了调制,在载波相位的跳变位置,信号瞬时频率会产生突变,如果直接对信号进行分段滤波处理,可能会丢失信号的部分信息,需要对信号做预处理。
首先通过平方倍频去除LFM-BPSK复合调制信号的相位编码信息,转化成带有噪声的线性调频信号,此时,信号的初始频率与调频斜率为原信号的2倍。平方倍频后的信号为
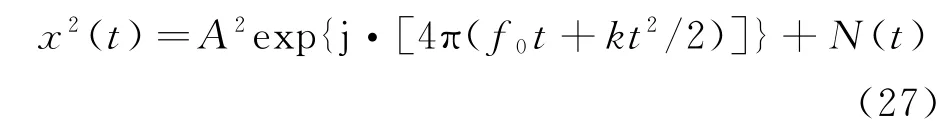
式中:N(t)=2A·exp[j·(2πf0t+πkt2)]·n(t)+n2(t)为LFM-BPSK复合调制信号平方后的等效噪声。
对原复合调制信号的平方处理导致输出信噪比降低,将对信号参数估计的精度产生影响。为提高参数估计的精度,采用文献[9]提出的改进算法对信号进行分段滤波处理。然后采用优化FRFT算法估计平方倍频后的LFM信号的初始频率和调频斜率。具体步骤如下:
a)步骤1:对LFM-BPSK复合调制信号进行平方处理,得到倍频的LFM信号;
b)步骤2:对倍频后的LFM信号采用优化的分段滤波算法进行降噪处理;
c)步骤3:利用优化FRFT算法依次进行粗估计和精确估计得到初始频率和调频斜率的估计结果为2^f0、2^k;
d)步骤4:由于对原LFM-BPSK复合信号进
假设信号初始频率及调频斜率具有较高的估计精度,则Δf→0,Δk→0,则sB(t)信号的表达式为
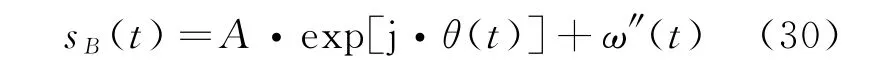
信号sB(t)为带噪声的BPSK信号,因此可利用循环谱相关法估计信号码速率Rb。具体流程如下:
a)步骤1:计算信号sB(t)的循环谱相关函数(f),得到|(f)|;
b)步骤2:在(α,f)二维平面上搜索α=0,特征谱模值|(f)|对应的频率fmax,则相位编码信号的载波频率的估计值为fc=fmax;
c)步骤3:由步骤2得到信号载频fc,在频率f=fc的平面上,在循环频率α=0的附近求特征谱模值|(f)|的次峰值,其对应的循环频率分别为α1、α2,则信号的码元速率的估计值为fd=(|α1|+|α2|)/2。行了平方倍频处理,因此由步骤3的估计结果除以2便可得原信号的估计值初始频率^f0和调频斜率^k。
得到初始频率^f0和调频斜率^k的估计值后,对线性调频信号进行重构:
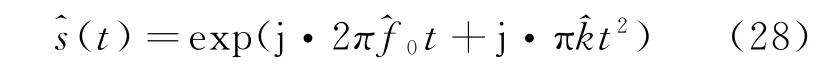
将重构信号与LFM-BPSK复合调制信号共轭相乘,得到信号sB(n)为
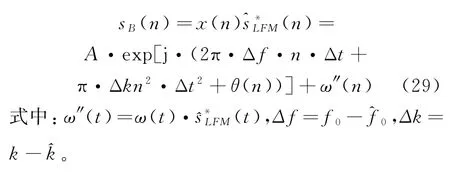
3 仿真实验
为验证上述参数估计算法的有效性,构造LFM-BPSK复合调制信号进行仿真实验,设置信号参数:初始频率f0=30 Hz,调频斜率k=200 Hz/s,相位调制码元宽度为0.1μs,码元个数为n=1 000,采样频率为fs=800 MHz。在信噪比为SNR=5 d B的条件下,分数阶傅里叶变换的初始估计及精确估计的三维仿真图及重构的BPSK信号循环谱相关图如图2和图3所示。
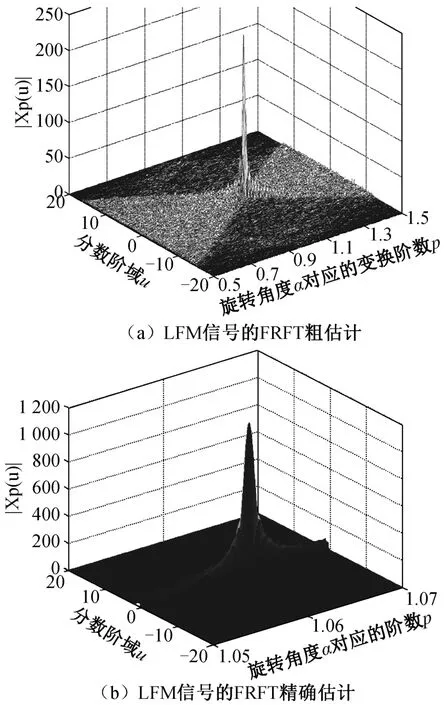
图2 LFM信号的FRFT粗估计及精确估计三维图
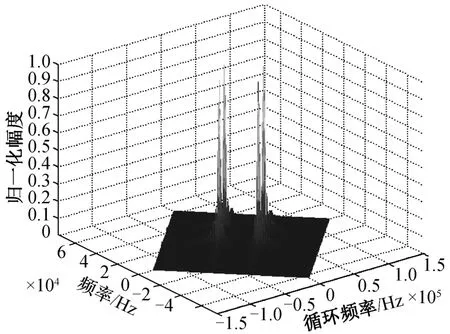
图3 重构的BPSK信号循环谱相关图
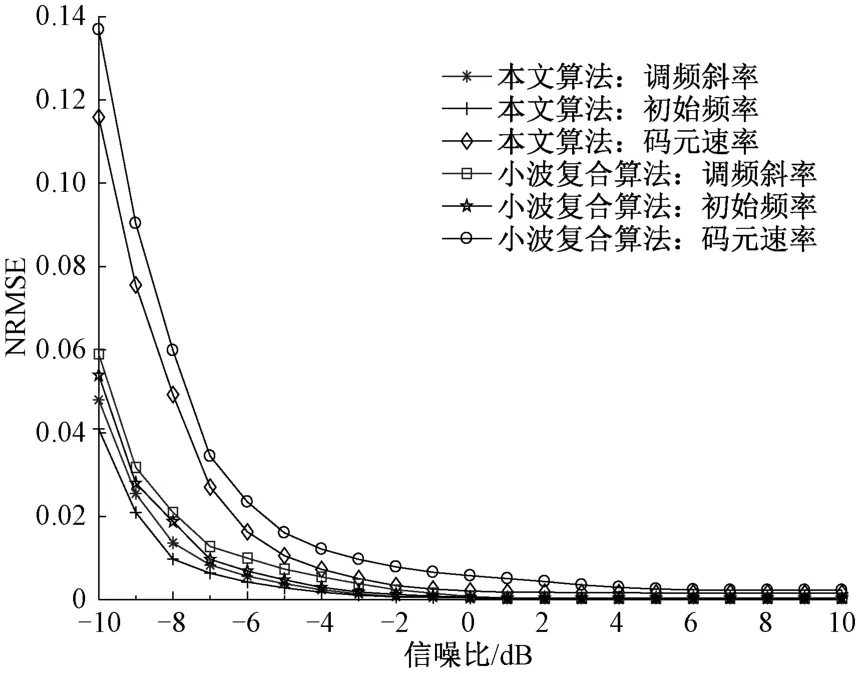
图4 不同算法参数估计的NRMSE曲线
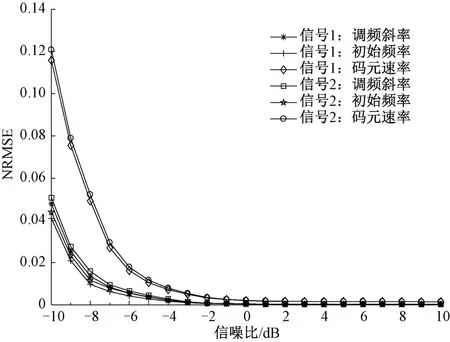
图5 不同信号参数估计的NRMSE曲线
在信噪比SNR=[-10 dB,10 dB]的区间内,每次间隔1 dB,进行蒙特卡罗仿真实验200次,分别对本文算法和小波复合算法的参数估计性能进行对比实验,仿真实验得到的不同信噪比条件下两种方法对LFM-BPSK复合调制信号的参数估计的归一化均方根误差(NRMSE)如图4所示。
由图4所示的仿真结果可以看出,针对LFM-BPSK复合调制信号的参数估计,在相同条件下对信号码元速率的估计精度均低于信号调频斜率以及初始频率的估计精度。小波复合算法和本文采用的算法在信噪比较高时,参数估计的效果都很好,但当信噪比较低时,本文算法对信号各参数估计精度要好于小波复合算法。整体而言,针对LFM-BPSK复合调制信号不同参数的估计精度,本文采用的算法的性能略优。但是,由于优化的分数阶傅里叶变换进行了插值补偿的优化,计算量比其他算法有所增加,采用在分数阶域先大步进粗搜索再缩小范围进行小步进精确搜索的方法,可以有效提高参数估计的效率。
为验证参数估计算法的有效性,重新构造一个LFM-BPSK复合信号参数:初始频率f0=50 MHz,调频斜率k=300 MHz/s,相位调制码元宽度为0.1μs,采样频率为fs=800 MHz。对两个信号在相同条件下进行参数估计对比实验,仿真结果如图5所示。可以看出,初始频率和调频斜率较大的信号2比信号1在信噪比较低时的参数估计误差略高,且对码速率的估计误差要大于对初始频率和调频斜率的估计误差,但两个信号的参数估计整体效果接近,充分说明本文采用的参数估计算法的稳定性。
4 结论
本文针对LFM-BPSK复合调制信号的特点提出一种FRFT和循环谱相关联合参数估计方法。对LFM-BPSK复合信号的起始频率、调频斜率和码元速率进行了估计。该方法具有较好的抗噪性和估计精度,在没有任何先验知识的条件下即可在低信噪比下精确估计复合信号的参数。
通过对不同信号的仿真实验结果表明本文方法具有良好的稳定性。但是由于需要在分数阶域的二维平面进行峰值搜索,所以运算量较大。
