基于视觉选择性的离变焦图像序列慢变特征提取算法研究
2020-01-14赵彦明
赵 彦 明
(河北民族师范学院数学与计算机科学学院 河北 承德 067000)
0 引 言
慢变信号是不变量的表达形式,是高频输入信号在高层表达上抽象的不变量信息。慢特征分析算法是基于不变量学习的分析算法,用于提取信号的慢属性和属性间的慢拓扑,并在诸多领域成功应用。
在1989年,Hinton[1]首次给出慢变特征的基本概念、基本理论和假设,初步形成慢变特征提取理论。2002年文献[2]提出慢变特征分析算法(SFA),该算法是一种非监督学习算法,通过特征空间的非线性扩张算法,有效解决了监督学习算法的样本数量不足与恒维等现象。慢变特征分析的理论和算法被建立。
2005年Berkes[3]和Wiskott将不变量学习成果应用于复杂细胞感受野学习模型研究上。2007年文献[4]研究并揭示不变量在马海体细胞上的性质,为不变量学习理论鉴定了生理学基础。2008年文献[5]利用慢变特征分析算法实现了卡通鱼位置与旋转角度的不变特征提取与识别,首次证明了慢变特征算法有能力提取分类信息,为慢变特征算法在特征提取与模式识别领域内应用提供了理论与实验基础。
文献[6]于2009年研究利用马尔科夫链生成训练数据训练慢变特征分析算法。证明当小参数a趋近于0时,慢变特征算法抽取的特征与FDA算法抽取的特征等效,证明不变量特征提取算法在特征提取上是正确可行的,同时证实马尔可夫链在慢特征训练上的可行性。
2011年马奎俊等[7]提出基于核的慢变特征分析算法,解决了特征空间扩充问题和避免在高维空间的运算问题,实现了慢变特征分析算法在盲信号分离上的应用。至此,标准慢特征分析算法已初步成熟。
为降低标准慢特征分析算法计算复杂度,受分治策略启发,文献[8]提出层次化的慢变特征分析算法,缓解计算复杂度过高问题,但是该算法因分层结构而损失相当一部分信息,不能确保算法能够提取全部的全局优化特征。为改进信息损失引起的特征提取非完全全局最优特征问题,以图论为基础,文献[9]提出了基于图论的慢变特征分析算法(GFSA)。该算法提出利用训练图的复杂结构来训练慢变特征分析算法的思想,该算法初步提出根据训练图像自身的复杂结构特征实现特征提取。2015年赵彦明等[10]提出了基于自然图像复杂视觉信息的特征提取算法,从视觉选择性角度,以自定义的TICA,提取自然图像复杂视觉空间信息与信息间的拓扑关系的慢特征,揭示视觉选择性与慢特征之间的一致性。
近年来慢变分析算法在人类行为识别[11-13]、忙信号分析[7,14]、动态监测[15]、3D特征提取[16]和多人路径规划[17]等不同领域上取得较好的应用。
慢特征分析方法在理论与应用上取得较好进展。但是,仍然存在如下两点缺欠:(1) 尽管慢特征分析方法已经采用训练图的复杂结构来训练慢变特征,但是传统慢特征分析方法提取的慢变特征不能揭示自然图像的视觉空间拓扑结构;(2) 没有利用图像序列的序列性和序列变化的视觉慢变性实现基元素的非线性扩张。
基于此,本文提出基于视觉选择性的离变焦图像序列慢变特征提取算法,解决了上述缺欠。
1 离变焦图像序列
在对自然图像分析上,慢特征分析过程具有与灵长类动物视觉皮层复杂视觉细胞视觉成像相近的特征[18]。灵长类动物的视觉系统对外界环境观察的过程中,传感信号和环境表示都是时域上的快速变化函数,频域上的高频函数,而其本质特征则是随时间缓慢变化的,即信号中包含的基函数空间与空间中基函数的拓扑关系变化缓慢,灵长类动物的视觉处理过程是多通路并行,每通路分层串行处理的过程[19-20];视觉选择性理论[10]:在视觉空间中,相同或相近子功能的视觉细胞分布在相同视觉区域,不同子功能的视觉细胞分布在不同视觉区域。
自然场景的离变焦图像序列采集过程类似于灵长类动物视觉系统对外界环境的观察过程。该过程是不同视距、视角和运动条件下,自然图像包含的视觉信息变化过程。离变焦采集系统采集的离变焦图像序列包含的传感信号与环境信号表示都是时域上快速变化的函数与过程,是频域上的高频函数。而离变焦图像序列视觉空间本质特征,则是随时间缓慢变化的,是快速变化的图像序列包含的传感信号与环境信号表示中的基函数空间与基函数空间的拓扑结构的不变性。
因此,本算法以灵长类动物的视觉选择性为理论基础,以慢特征分析为方法,提取离变焦图像序列中能够反映自然图像离变焦图像序列的视觉空间基的种类、每类元素数量、类内与类间拓扑结构不变性的Gabor特征。
2 算法比较
2.1 现有算法
初步分析SFA算法的理论与应用进行概述与分析,并归纳出传统SFA算法的优势与缺欠。现有算法的工作成果如表1所示。

表1 现有算法工作成果比较表
基于表1的比较分析结果,本文将重点从慢特征提取方法、慢特征扩展方法和特征结构方面改进,实现满特征算法与视觉选择性有效结合,实现离变焦图序列的特征提取与识别。下面将逐条论证算法改进与改进结果。
2.2 算法改进
离变焦图像是一个广泛的定义。在研究离变焦图像特征提取与分析时,应该限定离变焦的研究范围和研究约束。本文研究的离变焦图像序列是不改变图像视觉空间基的组成信息及拓扑结构的离变焦图像集合。这是在视觉空间内研究离变焦图像的基本约束,称为有限离变焦约束准则。
基于此,离变焦图像表达为:
I(k)={IB(k,i,t),t=1,2,…;i=1,2,…,Nk}
(1)
式中:IB(k,i,t)是第k个待研究离变焦图像的第i视觉基空间的第t个视觉功能区。Nk表示有限离变焦约束系数,以此保证本文算法提取离变焦图像序列不变性视觉特征的一致性。计算方法为:
(2)
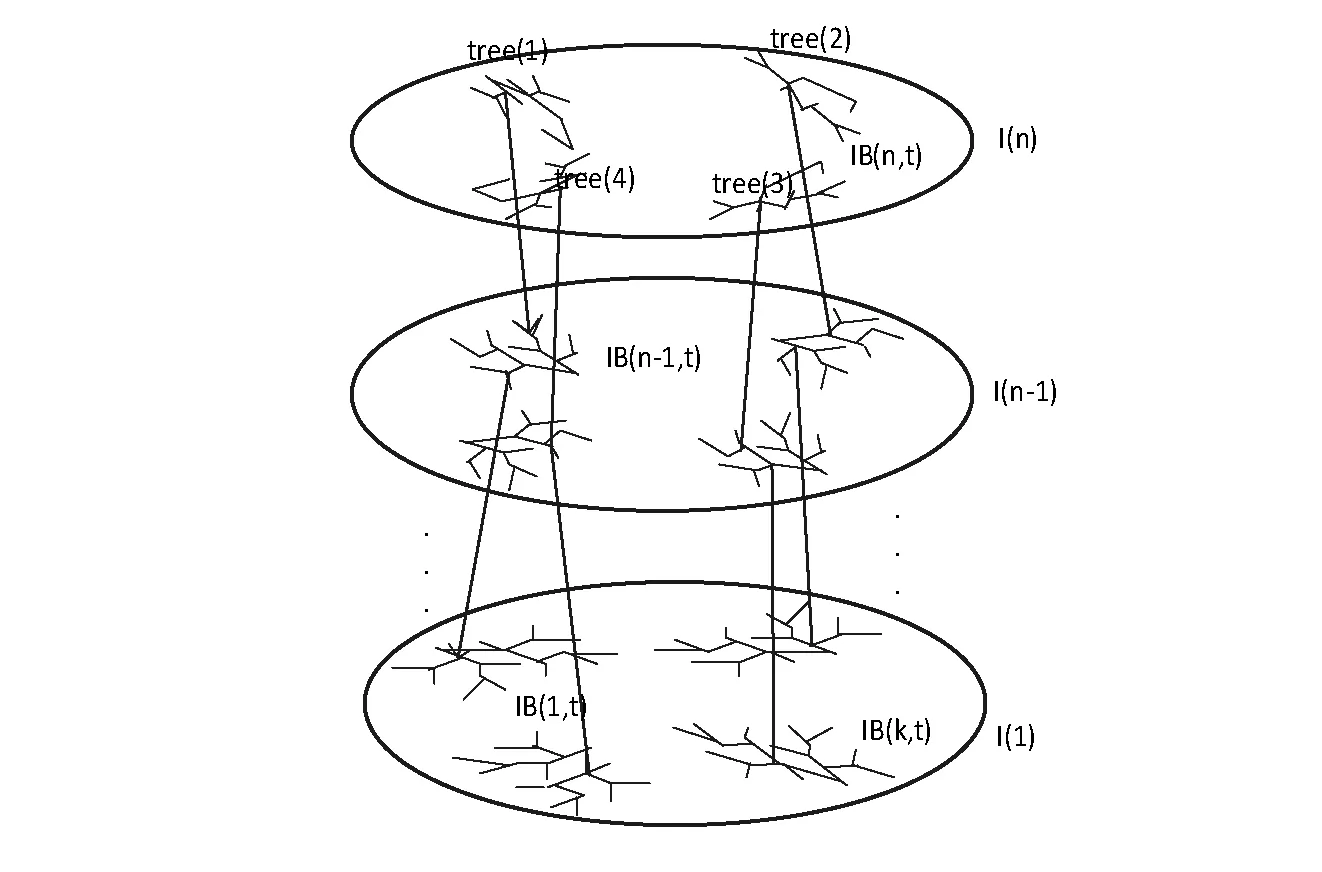
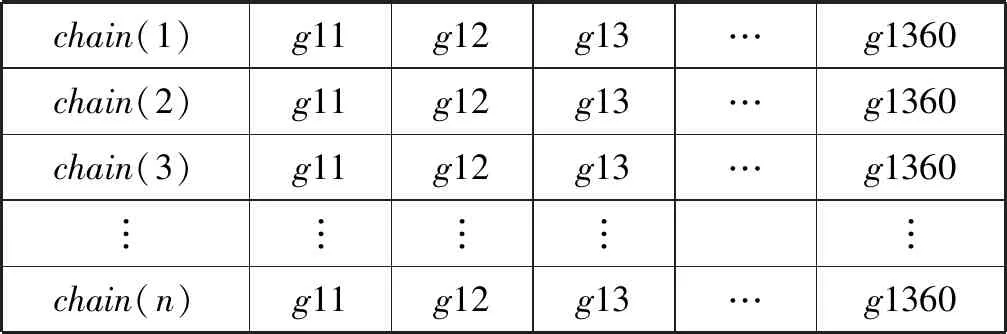
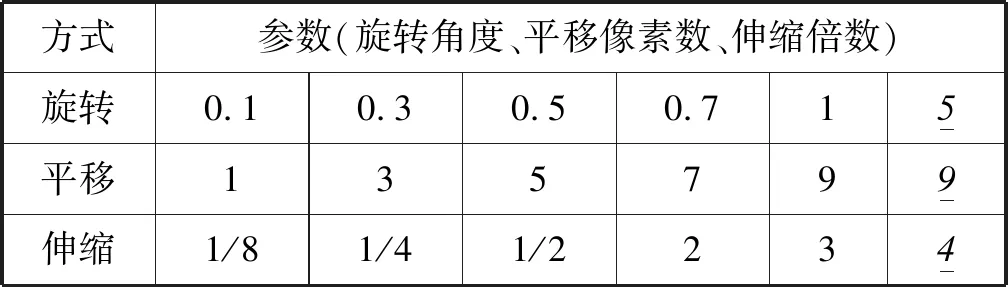
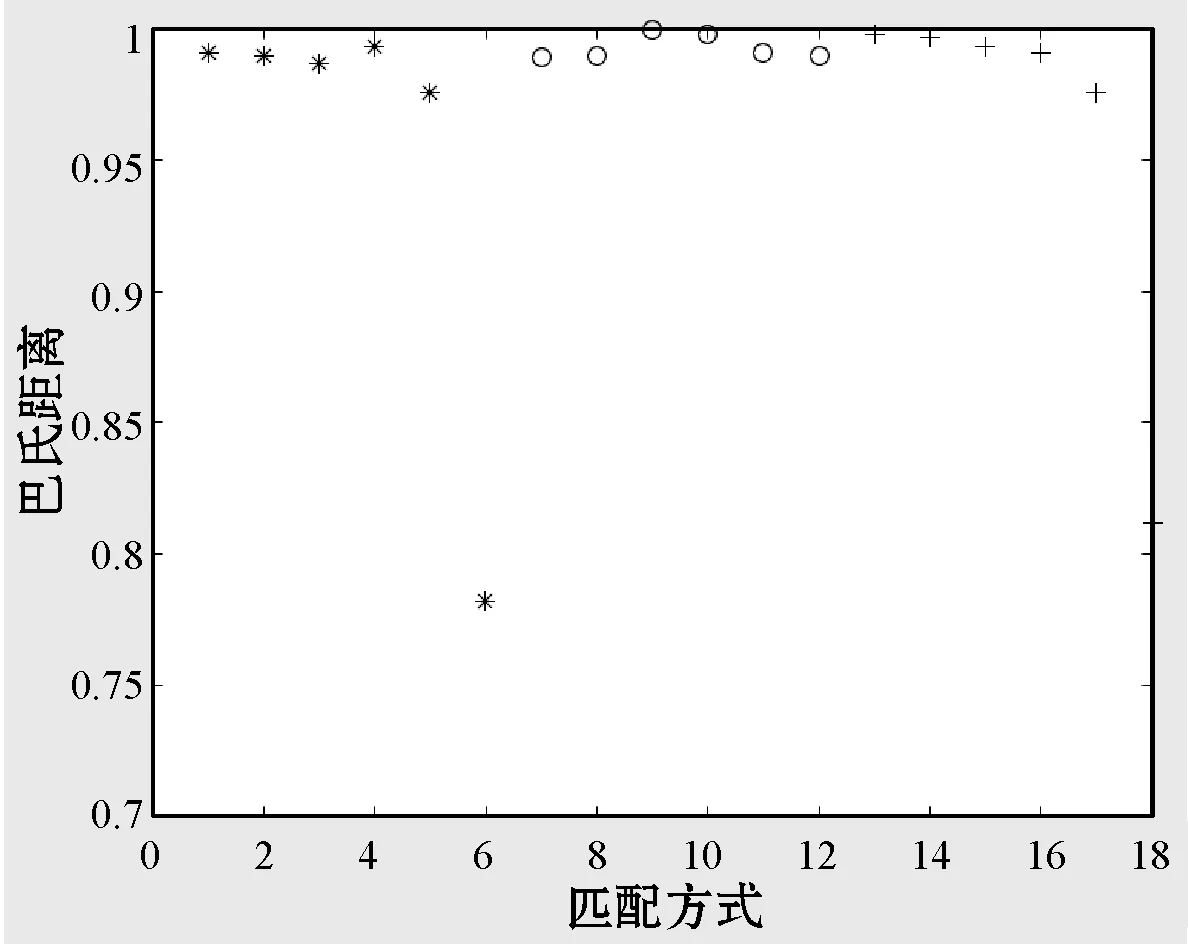
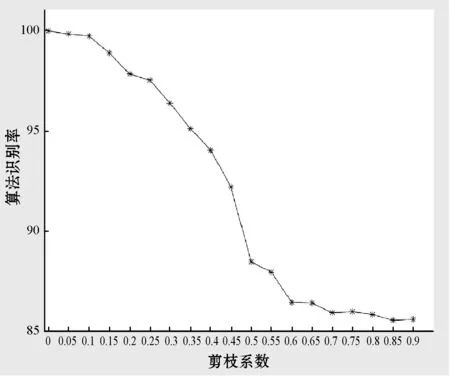
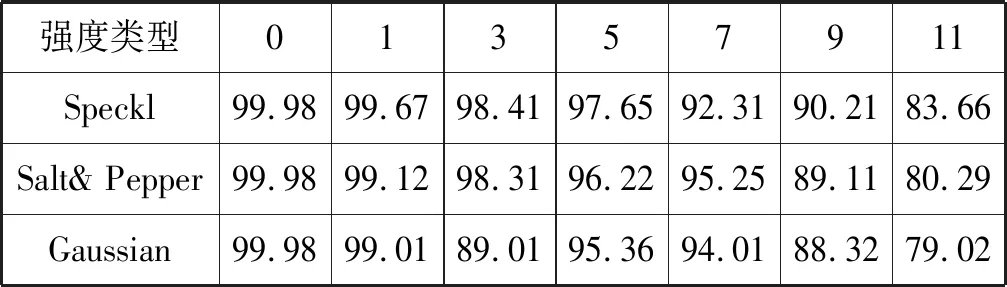
式中:IB(k,i,t)是第k个待研究离变焦图像的第i视觉基空间的第t个视觉功能区。Tall表示特征学习完成后第k个待研究离变焦图像的基空间的个数|I(k)|,且T 受有限离变焦约束准则限定,本文离变焦图像序列定义为:GI={I(k),k=1,2,…,N}。 改进1特征提取方法改进。 原SFA算法的特征提取方法为PCA方法,主要提取图像的独立成分信息,并没有提取自然图像的视觉空间拓扑结构,不能从视觉本质上反映图像的视觉本质特征。受视觉选择性理论启发,IB(k,i,t)中的元素应该具有相近或相似的视觉功能,并且分布在视觉空间相近的位置,具有明显的视觉选择性。因此,以myTICA[20]方法替代源SFA算的PCA方法,提取能够反映自然图像离变焦图像视觉慢变特征。即IB(k,i,t)用Gabor函数模拟,表达为: I(k)={IB(k,i,t)|IB(k,i,t)=gabor(f,o,t), t=1,2,…;i=1,2,…,NK} (3) 式中:f表示频率,o表示方向角,t表示归一化分布位置。 改进2特征基扩展与优化方法改进。 原SFA算法的特征空间扩展方法为多项式扩展算法,计算复杂度高,并且没有与自然图像视觉本质信息相结合,从视觉本质特征上进行特征空间扩展,生成反映自然图像本质的超完备不变性特征集合。受人类视觉形成过程预备离变焦图像序列生成过程的一致性启发,本文利用马尔可夫蒙特卡洛(MCMC)算法替代源SFA算法的多项式扩张方法,实现特征空间非线性扩展。该扩展包括特征基内元素扩展和特征树上元素扩展,生成自然图像离变焦图像序列视觉不变性特征的超完备基,并利用自定义的近似正交剪枝算法实现不变性特征森林的优化,得到优化超完备基。具体实现如下: 以GI特征集合元素的分布作为先验概率,利用基于Gibbs方法的马尔可夫蒙特卡罗预测算法,实现超完备基扩展,并依据超完备基约束系数,生成满足用户需求的离变焦图像不变性的超完备基。并启用近似正交判别规则对超完备基进行剪枝操作,优化超完备基。同时对tree(m)链上数据采用相同的预测算法,实现链上数据的完备扩展。 超完备基约束系数定义为: (4) 该系数针对于自然图像视觉空间的每个基,该系数限定MCMC算法生成基不能主导本文算法,只能起到辅助作用。 近似正交判别规则和剪枝方法: 设任意向量α、β,则两个向量正交的判别条件为:α⊥β⟺<α,β>=0。因此,定义相似正交的等价条件为:<α,β>=ε,ε为任意小正数,称为剪枝系数,控制剪枝的程度。因此,当lim<α,β><ε时,两个向量近似正交,如果是非扩展生成向量,响应系数增加1,并剪枝其中一个,否则,直接剪枝;当lim<α,β>≥ε时,不进行剪枝。 改进3不变性特征形成。 原SFA算法仅提取自然图像的PCA特征,并没有根据自然图像自身的视觉特征提取离变焦自然图像慢变特征和特征间的空间拓扑关系。 因此,根据上述两步改进,在原SFA算法构架上改进,构造反映离变焦自然图像序列视觉不变性的特征森林,如图1所示。 图1 离变焦自然图像序列视觉不变性的特征森林 图中:tree(m)为离变焦图像序列的视觉空间第m序列的特征,m=1,2,3,…。该tree(m)是依据灵长类动物视觉信息处理全局并行,局部串行的理论设计的,有利于算法分布式并行设计。 综上所述,离变焦图像序列的慢变特征表达为: IS={tree(m)|m=1,2,3,…} (5) tree(m)={(index(m,j),gabor(m,j))} (6) 式中:m表示表示视觉空间基,j表示该视觉空间基中元素位置,j=1,2,…,360。IS矩阵的列具有频率选择性,行具有方向角选择性,排列方法为递增排列,且方向角范围规定为[1°,360°]。 因此特征描述如表2所示。 表2 特征矩阵index(每行包含360个特征) 表中:1表示该位置存在感受野;0表示该位置不存在感受野。而且每个index(i,j)节点处隐含与其对应的gabor(i,j)函数,这些函数组成特征矩阵GMindes,如表3所示。 表3 特征矩阵GMindex对应的感受野 S1:初始化训练图库指针k=1。 S2:从训练图库train_db中,提取离变焦图像序列GI={I(k)|k=1,2,…,N}。 S3:在图像I(k)上,按照窗口大小N1×N2,随机采样个数2 048×sample_number个子图像,生成训练子集train_sub_db(k)。其中采样次数sample_number是一个实验值,是防止算法过拟合的控制参数。 S5:如果i≤N,i=i+1,算法重复执行S2-S4步。否则,算法完成。 S6:当GI={I(k)|k=1,2,…,N}特征集合生成完毕,利用该集合元素作为先验概率,启动基于Gibbs方法的马尔可夫蒙特卡罗预测算法,实现各个基的超完备基扩展,并启用近似正交判别规则对超完备基进行剪枝操作,简化优化计算过程且保持超完备基特征。同时对tree(m)链上数据采用相同的预测算法,实现链上数据的完备扩展。 该扩展过程受超完备基约束系数和剪枝系数两个参数影响,其定义为: (7) 该系数针对自然图像视觉空间的每个基,并限定MCMC算法生成基不能主导本文算法,只能起到辅助作用。 近似正交判别规则如下: 设任意向量α、β,则两个向量正交的判别条件为:α⊥β⟺<α,β>=0。因此,定义相似正交的等价条件为: <α,β>=ε,ε为任意小正数,称为剪枝系数,控制剪枝的程度。 当lim<α,β><ε时,两个向量近似正交,如果是非扩展生成向量,响应系数增加1,并剪枝其中一个;否则,直接剪枝。 当lim<α,β>≥ε时,不进行剪枝。 S1:从测试图像集合test_db中提取一幅图片test_db(i)。 S2:在图像test_db(i)上,按照窗口大小11×11像素随机采样个数2 048×sample_number个子图像,生成测试子集test_sub_db(i,k)。 S3:从特征数据库中读取特征矩阵index和GMindex,设滑动尺度为1,按照自定义响应度计算方法,计算test_sub_db元素与特征矩阵GMindex的响应度。按照响应度计算规则,生成识别结果矩阵test_index(i)。 自定义响应度计算规则如下: 计算相似矩阵T: (8) 计算T矩阵每一列中内积值大于平均内积值的元素个数ref_number,并将该值赋值给test_index(i)行。 S4:利用基于巴氏距离的直方图匹配法计算test_index与index的相似性系数δ。将相似系数δ>δ0的类记录到识别结果recong_result(j)中。 S5:按照Softmax函数方法计算recong_result(j)矩阵识别结果。 根据第2节的理论分析,离变焦图像可由原始清晰图像通过仿射变换近似生成。因此,算法实验图库为从INRIA Holidays dataset图库中选区的1 000幅图像集,按照表4的前5列参数做仿射变换生成包含原始图像在内的研究图库,图库大小为15 000幅。该图库被分成两个部分,前12 000幅为训练图集train_set;后3 000幅为测试图集test_set,两个集合均包含原始图像1 000幅。图2显示了部分来自研究图库的图片样本。 表4 仿射变换表 图2 基于INRIA Holidays图库的实验图库样本 在INRIA Holidays dataset选取图像103901.jpg,按照采样窗口大小为11×11像素和采样次数为2 048次,在该图像上随机采样生成original_set子图像集,并依据文献[10]算法生成original_set_base视觉空间基集;按照仿射变换表参数设定,依据上面的过程生成不同参数下rotate_set_base(angle)、translate_set_base(pixels)和scala_set_base(scala)视觉空间基集。按照基于巴氏距离的直方图匹配方法,计算各个变换集合到原始视觉空间基集的巴士系数。结果如图3所示。 图3 bhattacharyya系数分布图 由图3可知:根据bhattacharyya系数分布图,在有限约束条件下,离变焦图像具有视觉慢变性。其中平移对巴氏系数影响非常小,图像平移具有最强的视觉不变性。旋转与伸缩对巴氏系数影响非常大,具有有限视觉慢变性,即约束范围内具有视觉不变性。实验验证,当旋转角度控制在1°范围内,算法具有严格的角度视觉不变性。伸缩尺度限定在[1/8,3]内,算法具有严格的伸缩视觉不变性。因此,实验图库生成严格按照该约束。 采样窗口大小对算法识别率具有较大影响,在不同采样窗口大小下,以训练图集train_set训练,并以测试图集train_set测试本文算法。结果如图4所示(窗口大小为n×n,其中n=3,5,7,9,11,13,17,19,23,29,33,37)。 图4 采样窗口大小对算法识别率的影响 由图4可知:随采样窗口大小增加,算法识别率先增加后区域稳定,原因为窗口大小过小时,算法局部特征过于明显,影响全局特征标书,造成识别率下降。而随采样窗口大小逐渐增高,全局信息与局部信息采集达到均衡,算法识别率逐渐增高后会趋于平稳变化。当采样窗口大小为11×11时,算法识别率为99.37%,具有较好的实用性。 当采样窗口大小为11×11时,采样次数为128、162、196、256、296、352、406、456、512、587、624、698、729、798、852、962、1 024、1 225、1 532、1 856、1 960、2 048、2 155、3 256、4 096、5 056、6 024、7 152、7 852、8 192次时,采样次数对算法识别效果的影响如图5所示。 图5 采样次数对算法识别率的影响 由图5可知:随采样次数增加,算法识别率呈现先增加后趋于稳定,原因为采样次数过少时,因采样算法会发生信息丢失,造成识别率下降。而随采样次数逐渐增高,信息丢失现象会被尽量避免,算法识别率逐渐增高后会趋于平稳变化。当采样次数为2 048时,算法识别率为99.67%,具有较好的实用性。 综上所述,当采样窗口大小为11×11像素,采样次数为2 048次时,算法具有较好的识别效果,可作为后续实验的约束条件。 根据上述实验结果,采样窗口大小为11×11像素,采样次数为2 048次,采用本文算法,在训练图集train_set和测试图集test_set上,研究剪枝系数和超完备基约束系数λ与本文算法性能的关系,如图6、图7所示。 图6 剪枝系数ε与本文算法性能的关系 由图6可知:当剪枝系数增加变化较小时,剪枝去除的基元素数量较小,基本上不会影响自然图像的视觉特征空间表达,因此,不会影响算法识别率;随剪枝系数增加,超完备基元素数目减小增加,会增加去除从自然图像直接提取的基元素,视觉空间表达效果降低,识别率下降;当剪枝系数增加到一定区域时,算法提取的基元素基本来自于自然图像直接提取,算法识别率不会发生明显变化。 由图7可知:当超完备基约束系数λ增加变化较小时,算法预测生成的基元素数量较小,对自然图像的视觉特征空间表达影响大,因此,对算法识别率影响较小;随超完备基约束系数增加,超完备基生成元素数目增加,将减小从自然图像直接提取的基元素对视觉空间表达效果贡献,导致识别率下降。 图7 超完备基约束系数λ与本文算法性能的关系图 综上所述,当采样窗口大小为11×11个像素,采样数为2 048,剪枝系数ε=0.15和超完备基约束系数λ=0.06时,本文算法识别性能最佳,识别率为99.87%。 选择采取采样窗口大小为11×11像素,采样次数为2 048次,剪枝系数ε=0.15和超完备基约束系数λ=0.06时,在训练图集train_set和测试图集test_set上。按照本文算法进行类内与类间bhattacharyya距离分布实验,结果如图8所示。 图8 bhattacharyya距离分布 可以看出,依据ROC(receiver operating characteristic)曲线,当实验阈值为0.4时,算法获得识别率为99.96%,误识率与误据率都小于0.02%。表明本文算法具有较强的分类能力。 选择采取采样窗口大小为11×11像素,采样次数为2 048次,剪枝系数ε=0.15和超完备基约束系数λ=0.06时。在训练图集train_set和测试图集test_set上,比较本文算法与SFA[1]、GSFA[8]、TICA[9]、myICA[10]性能,结果如图9所示。 由图9可知:与SFA[1]、GSFA[8]、TICA[9]、myICA[10]相比,本文算法具有高于其他算法识别率,原因是本文算法不仅提取自然图像的感受野信息,也提取感受野间拓扑关系,从视觉空间上构造信息+拓扑的特征结构,本质上表示自然图像的视觉特征,是其他算法所没有的。随采样窗口大小的增加,每种算法的识别率先增加后趋于稳定。当采样窗口大小为11×11时,各个算法均达到稳定识别率。当窗口过小时,算法抗噪声能力差,算法识别率低;当窗口大小过大时,提取的感受野可能会包含多个感受野信息,造成感受野局部性信息丢失,算法识别率低。 不同噪声强度、不同噪声类型(Gaussian、Salt&pepper和Speckl)会对识别率产生影响,当噪声过大时,将失去研究价值。因此,分析算法的抗噪性能,结果如表5所示。 表5 算法的抗噪性能表 % 由表5可知:随噪声强度的增加算法识别率显著减小,但是在噪声强度低于5%时,算法具有较强的抗噪能力。Gaussian噪声的函数表达式是gabor函数的一个子集,具有明显视觉“ON-OFF”选择性。因此,高斯噪声增加会改变局部视觉空间结构的基函数属性与特征,造成提取gabor函数不能表述原自然图像的本质属性,但是高斯噪声对拓扑结构影响不大。Salt&pepper具有黑白点噪声特点,具有体量较小视觉“ON-OFF”选择性。对局部区域特征提取具有较大影响,对区域性gabor函数提取具有较大影响,当采样窗口大小较小时,影响尤为严重,对全局与局部拓扑结构影响比高斯噪声大。与前两种噪声相比较,Speckl噪声具有单体结构大的特点,每个斑点噪声均可以形成独立的视觉gabor函数,可产生独立的视觉选择性,同时破坏原有自然图像的视觉选择性和视觉分块属性。因此,按照本文算法提取的感受野特征不能较好表示原图像视觉特征,算法识别率受到较大影响。整体上,在相同噪声强度下,Speckl、Salt&pepper和Gaussian对本文算法识别率影响依次减弱。 本文提出基于改进慢特征分析的离变焦图像序列特征提取算法。算法受自然图像视觉不变性理论启发,提取离变焦图像序列的视觉空间基的种类与类内元素数量、类内拓扑与类间拓扑结构的不变性特征建立图像序列的视觉不变性特征森林,解决了慢变特征提取算法忽视自然图像自身所包含的复杂视觉特征不变性问题;提出慢变特征森林从本质上描述离变焦图像的视觉不变性本质。通过蒙特卡洛马尔可夫算法预测生成新的基元素,解决采样算法造成的自然图像的基元素丢失问题,并降低基扩张部分的计算复杂度;利用自定义的近似正交剪枝算法实现森林剪枝,优化不变性特征森林,并利用自定义响应度计算规则实现匹配算法。从理论与实验角度,通过大量实验验证本文算法。实验结果表明:与同类算法相比,该算法正确可行,具有较好的抗噪能力;在实验阈值为0.4时,算法获得识别率为:99.96%,误识率与误据率都小于0.02%,这说明本文提取的算法具有较强的分类能力。 未来将深入研究依据自然图像视觉本质特征自适应设定蒙特卡洛马尔可夫算法参数问题,使其在视觉计算领域取得更好的应用效果,并展开该算法在信号识别领域应用探索。
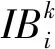

3 算法设计
3.1 特征提取算法
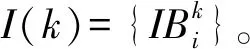

3.2 识别算法
4 实验及分析
4.1 实验图库生成与展示

4.2 离变焦图像视觉不变性验证
4.3 采样窗口大小与采样次数对算法识别性能的影响


4.4 超完备基生成参数对算法识别性能的影响

4.5 算法可行性评价

4.6 算法识别性能比较
4.7 算法抗噪性能分析
5 结 语
