浅显处亦是思维的提升处
2020-01-13王广阔
王广阔
(江苏省徐州市铜山区新区实验小学,江苏徐州 221116)
引 言
谈到发展思维,我们总会自然而然地想到难题,甚至认为只有挑战难题,才能发展思维。在这种潜意识的影响下,我们往往会忽略一些浅显的问题,漠视习以为常的小题,不愿在小题上花时间,不愿在浅显处费周折,殊不知,却因此失去了众多发展学生思维的契机[1]。
例如:2.7里有( )个0.1或( )个0.01。
数感好的学生会直接填上27、270。如果学生的数感不好呢?大约有三分之一的学生面对此问题时不知所措,我们该怎样教?另外三分之二填出正确答案的学生,也是把问题的解决建立在感觉之上吗,可靠吗?如此追问下去,我们很容易发现:这个我们认为的“浅显问题”对学生来说并不浅显。越是我们认为浅显而学生却不能完全理解的问题,对我们的教学来说越是极大的挑战。该怎样教呢?课堂上,笔者从以下四个路径出发引导学生对“浅显问题”进行了深入思考。
一、基于小数意义的形象思考
这个问题考查的是学生对2.7这个小数的意义以及小数计数单位的理解。其实,在整数范围内,也经常有类似的考查。例如,270是(27)个十或(270)个一。在小数范围内考查,学生却不适应,恰恰反映出学生对小数意义和计数单位的理解还不够透彻。数形结合是深化意义理解的必要手段[2],因此,笔者让学生在正方形内表示出2.7,然后分别在其中找出0.1和0.01,再借助图形进行思考(见图1)。
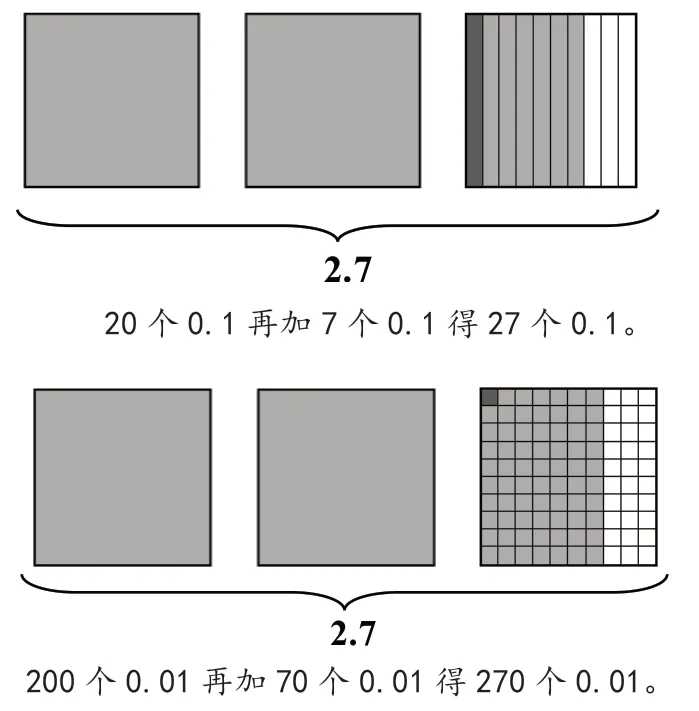
图1
有了图形的支撑,学生能够直观形象地理解为什么2.7是27个0.1,又为什么是270个0.01。再遇到类似的问题时,学生就可以利用画图的方式去思考。虽然一开始显得比较麻烦,但小数的意义的表象正是在这样的画图中完成的,学生的数感也是在这样的画图中获得提升的。
二、基于分数意义的抽象思考
小数的本质是十进分数,因此,借助分数来解决上述问题,也是比较好的方法。2.7是一位小数,表示是27个也就是27个0.1。同理,2.7是一位小数,改写成两位小数是2.70,也就是是270个也就是270个0.01。当然,这样的表述不能变成绕口令,而要基于图形表象的支撑。
三、基于相邻进率的演绎推理
十进制的位置值是小数与整数的联系点。1是10个0.1,0.1是10个0.01……学生根据进率关系也可以进行思考。2是20个0.1,0.7是7个0.1,合起来是27个0.1;2是200个0.01,0.7是70个0.01,合起来就是270个0.01。借助下面的分成图(见图2)来表示,可以让学生获得更加清晰的认识。
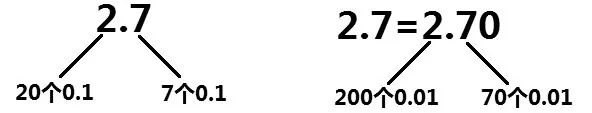
图2
四、基于相同单位的形式化比较
学生产生思考障碍的原因往往是数字的单位不同造成的,而改成相同单位后,就有利于学生观察[3]。2.7与0.1的计数单位都是0.1,因而直接去掉2.7的小数点就可以得到2.7是27个0.1。2.7与0.01的计数单位不同,先把2.7改写成2.70再和0.01比较,很容易看出,2.70是270个0.01。这种形式化的思考,因为有上述三种方法的支撑而不仅仅是简单的技巧,同样也具有优化学生思维的价值。
一个简单的问题,采用了四种不同的思维路径去教学:图形思考、意义思考、进率思考、形式化思考。这四种不同的方法不是孤立的,而是有联系的。画图是基础,是进行抽象思考与演绎推理的基础,形式化的思考技巧性很强,没有前面三种方法的支撑,没有画图说理之后逐步形成的数感,形式化的思考就偏离了数学的本义变成了形式主义。因此,教师要循序渐进地引导学生理解以上四种方法。一个浅显的问题,教师不能直接教解题技巧,而要从形象化的方式入手,逐渐实现抽象的理解,进而帮助学生形成良好的思维习惯和数感。这样的教学过程是合理的,是讲理的,是有根的,是利于学生理性思维发展的。
以此题为基础拓展开去,教师还可以进一步引导学生做逆向思考的问题,如36个0.1是( ),36个0.01是( );也可以把类似问题放在一起做对比思考,如“3个0.1与6个0.01组成的数与36个0.001组成的数相等吗?”这同样也是浅显的小问题,但依然需要引导学生进行深入思考。
结 语
综上所述,数学不是由繁难的问题堆积起来的,而是由众多浅显的小问题串联叠加起来的,但是我们不能因为数量多且浅显而忽视,相反,应该因此而更加重视,正是这一个个的浅显问题逐步纳入学生的知识体系,才构建起了学生的认知结构。重视对浅显问题的深入探究,才能充分调动学生已有的知识来解决问题,将不同的知识勾连起来,才能发展学生的思维,提升学生的数学素养。数学是由万千的浅显问题组成的,再浅显的问题,都要多去思考怎样学、怎么教,做到简单的问题不简单地教。浅显处,是每天数学课的常见之处,繁难之题不过偶遇,思维的提升依靠的是日积月累,而不能靠一蹴而就,因此,浅显处才更是思维的提升处。
