三阶导及其几何意义及在高考中的应用
2020-01-11谢朝
数学学习与研究 2020年22期
关键词:高考
谢朝

【摘要】三阶及以上的导数称为高阶导,高阶求导在资料中很常见,最明显的就是泰勒级数.众所周知,一阶导的几何意义是斜率,可以表示增减,二阶导的几何意义是一阶导的斜率,可以表示凹凸,对于三阶导的几何意义,本文将做一些直观說明,并进一步得出偏移不等式结论,以及本结论在高考中的巨大作用.
【关键词】二阶导;琴生不等式;三阶导;几何意义;偏移不等式;对数平均;高考
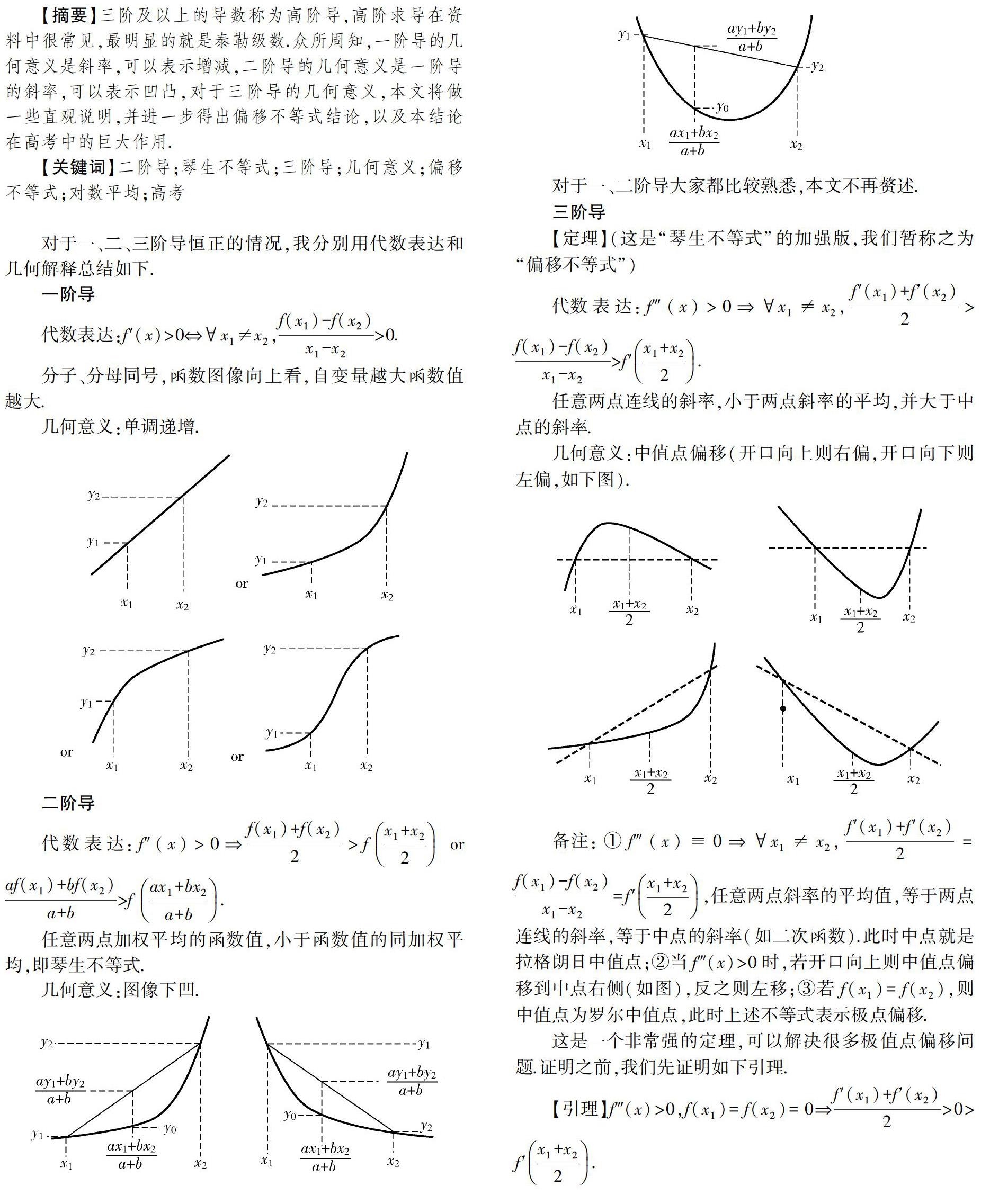
对于一、二、三阶导恒正的情况,我分别用代数表达和几何解释总结如下.
以上问题除例3都是高考中的压轴题,但都可用“偏移不等式”秒杀,类似的题目很多,由于篇幅问题,本文就不一一讲解.另外,本定理用泰勒展开也很容易证明.留给读者继续研究.
【参考文献】
[1]蔡德华.浅谈高考导数压轴题中的优化运算技巧[J].数学通讯,2019(1):39-43.
[2]尤新建.巧妙构造辅助函数发展数学核心素养“导数的应用”微专题教学设计[J].数学通讯,2018(12):31-33.
[3]李宁.与极值点有关的多元最值问题的解题策略[J].数学通讯,2019(2):1-4.
[4]柏庆昆,李思念.一道导数压轴题的“溯源”与“深延”改编[J].数学通讯,2019(16):42-44.
