Lua脚本在有限元分析中的应用

宋小鹏 何秀锦 古小敏 吴国珊 王斌武

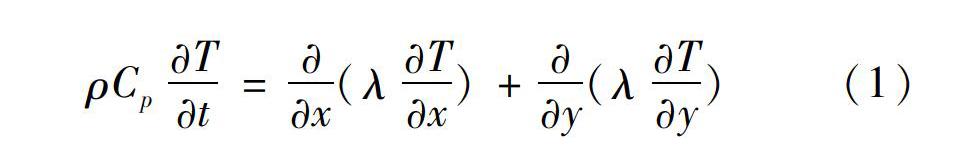
摘要：

针对复杂计算域有限元分析前处理过程中手动建模和边界条件设定烦琐和耗时的问题，以蓄热砖温度场分析为例，讨论Lua脚本在有限元前处理过程中的应用;开发温度场有限元分析程序，基于Lua/C API定义若干接口，使用特例的解析解验证温度场计算结果，基于Lua脚本对蓄热砖温度场进行计算。仿真结果表明，Lua脚本可简化有限元前处理过程，特别是几何建模过程，也便于对计算结果进行参数化分析。

关键词：

蓄热砖; 温度场; 前处理; 有限元

中图分类号：  TU522.07; TB115.1

文献标志码：  B

Application of Lua script in preprocessing

of finite element analysis

SONG Xiaopeng， HE Xiujin， GU Xiaoming， WU Guoshan， WANG Binwu

（

School of Energy and Building Environment， Guilin University of Aerospace Technology，

Guilin 541004， Guangxi， China）

Abstract：

As to the issue that the manual modeling and boundary condition setting are tedious and timeconsuming in the preprocessing of finite element analysis in complex computing domain，  the application of Lua script in the preprocessing of finite element is studied

by taking temperature field analysis of thermal storage brick as an example. The finite element analysis program for temperature field of thermal storage brick is developed. The interfaces based on Lua/C API is defined， and the calculation results of temperature field are verified by the analytic solution of a special case. The temperature field of thermal storage brick is calculated based on Lua script. The simulation results show that the preprocessing of finite element， especially the geometric modeling process is simplified using the Lua script， and the parametric analysis on the computing results is easy to be completed.

Key words：

thermal storage brick; temperature field; preprocessing; finite element

0 引 言

Lua脚本程序具有跨平台性能好、执行速度快、支持热更新、可扩展性能好等优势，常用于程序配置。[12]陆乔[3]在不更新应用程序的前提下，基于Lua脚本实现动态增加程序功能的目标。程君[4]以Lua脚本作为移动互联网中间件，解决不同平台的编程接口差异导致信息传递不畅的问题。宋宏江等[5]基于Lua脚本编制验证程序，明显提升卫星综合测试过程中指令生成的效率。

大量科研工作者已对蓄热砖的蓄热特性进行分析，如：赵頔等[6]使用ANSYS软件分析蓄热砖蓄热特性，分析结果与实验研究结果较为一致;徐德玺等[7]基于有限元法计算蓄热砖孔道直径与其热效率之间的关系。蓄热砖的孔道形状和布置对其蓄热特性有显著影响：胡思科等[8]研究圆形与方形孔道固体蓄热砖的蓄热和放热特性;李晶晶等[9]研究固体蓄热装置的自然对流放热特性受圆形和椭圆形孔道布置的影响。

有限元分析是研究蓄热材料温度场的重要手段。在蓄热砖有限元分析过程中，当孔道数量较多时，孔道的建模和边界条件设置较为烦琐。本文以蓄热砖温度场分析为例，探讨Lua脚本在有限元分析过程中的应用，旨在提高有限元建模和计算效率。

1 蓄热砖数学物理模型

1.1 物理模型

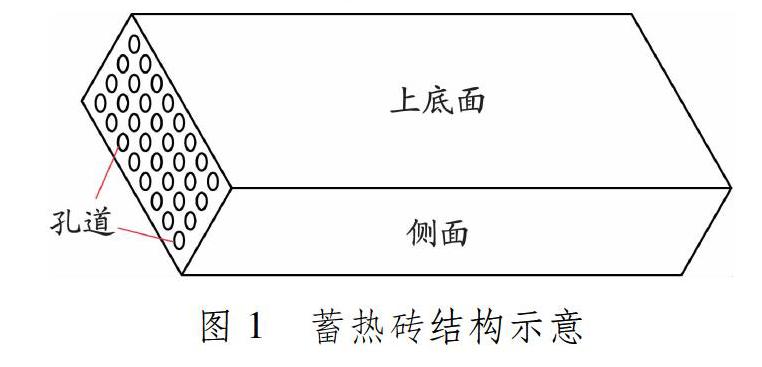
计算采用的蓄热砖结构示意见图1，其底面宽为0.4 m，底面长为1.0 m，高为0.2 m。在蓄热砖长度方向上布置若干孔道，用于蓄热后释放显热，其中孔道半径为14 mm，孔道中心间距为45 mm。蓄热砖底面通过电阻丝加热，以增加蓄热砖显热。

1.2 数学模型

1.2.1 控制偏微分方程

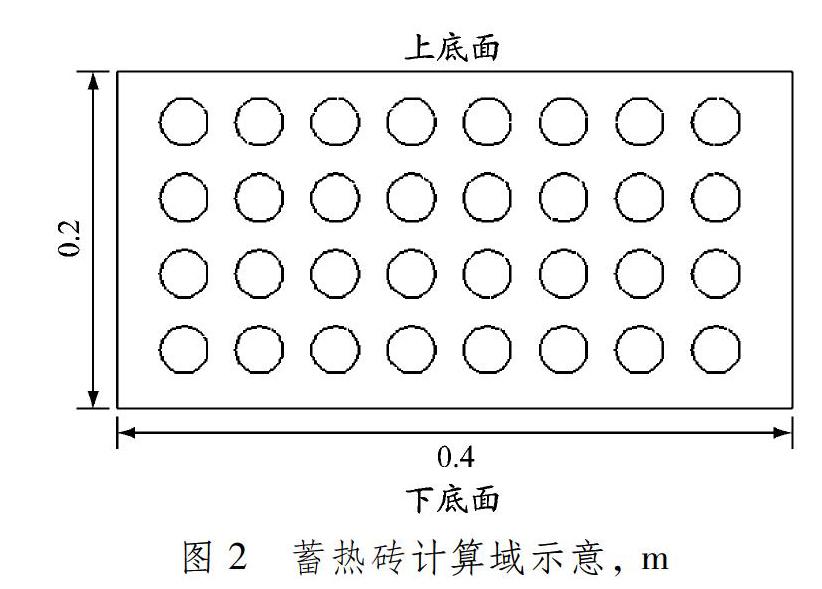
蓄热砖沿孔道方向较长，在蓄热过程中热量的主要傳递方向为由下底面到上底面。为减少计算量，可只计算蓄热砖横截面上的温度分布，故其计算域见图2。

在蓄热砖蓄热过程中，孔道内无流体的强迫流动，可仅考虑热传导，因此其控制偏微分方程为

式中：T为蓄热砖温度;t为蓄热时间;ρ、Cp和λ分别为蓄热砖的密度、定压热容和热导率。

1.2.2 定解条件

蓄热砖初始温度为20 ℃，下底面由电阻丝提供

恒定热流加热，热流密度设定为2 500 W/m2，连续加热10 h，假设蓄热砖的其他边和孔道内部均为绝热边界条件。蓄热砖主要材料为氧化镁，假设加热过程物性参数恒定，其密度为3 000 kg/m3，定压热容为1 kJ/（kg·K），热导率为3 W/（m·K）。

2 温度场有限元求解过程

2.1 求解过程

在有限元计算过程中，先结合边界条件对计算域进行网格划分，将计算域离散为有限数量的三角形单元，根据单元形状函数、边界条件和物性参数等计算各个三角形单元的单元系数矩阵。使用伽辽金加权余量法计算稳态温度场并合成全局矩阵，得到关于温度场的代数方程。代数方程求解完成后，对计算结果进行后处理。

2.2 Lua脚本封装

使用C+编写二维温度场有限元计算程序，编写5类关键接口，实现几何模型计算域的设定、定解条件（边界条件、初始条件、材料属性等）的定义、网格划分、代数方程求解和结果输出等。将C++程序编译为可执行程序，使用配置文件设定程序执行过程中的参数。Lua脚本解释器体积小、执行速度快，可用于程序配置文件。与常规配置文件相比，Lua脚本配置文件可以执行各类复杂数学运算，支持循环语句、条件转移等常规语言具有的特性。本文使用Lua配置有限元程序，在C++中通过Lua/C API定义9个关键内置程序接口（见图3），用于Lua脚本调用。通过编写Lua脚本，实现通用二维温度场有限元分析程序的几何模型计算域定义、定解条件设定、网格划分、计算和结果输出。

3 计算结果与讨论

3.1 程序验证

为评估有限元程序计算结果的准确性，在矩形

假设边界条件为T|x=0=Ay（b-y）、T|x=a=0、T|y=0=Bsin（πx/a）和T|y=b=0，根据数学物理方法中的分离变量法[10]，可得到其解析解为

编写Lua脚本以求解该温度场。定义边界条件、材料热物性参数和几何模型计算域的Lua脚本如下。

1. a，b=50，30 矩形计算域长度和宽度

2. addBC（1，0，0，"10*sin（3.1415926*x/50）"） 左侧边的边界条件 #01

3. addBC（1，0，0，"0.05*y*（30y）"） 下侧边的边界条件 #02

4. addBC（1，0，0，""） 上侧和右侧都是绝热边界条件 #03

5. addMaterial（34，7200，680，""） 定义材料热物性：导热系数，密度和比热容

6. addNode（0，0）计算域左下节点

7. addNode（a，0） 计算域右下节点

8. addNode（a，b） 计算域右上节点

9. addNode（0，b） 计算域左上节点

10. addLineSgmt（0，1，1，1） 计算域下底边边界条件为#01

11. addLineSgmt（1，2，1，3） 计算域下底边边界条件为#02

12. addLineSgmt（2，3，1，3） 计算域下底边边界条件为#03

13. addLineSgmt（3，0，1，2） 计算域下底边边界条件为#02

14. addDomain（25，15，1，10） 设定计算域材料为#01，最大三角形单元面积为10

15. iterations，timsStep，initialValue，coordnate=1，0，0，0  迭代次数、步长和初始值

16. Solve（iterations，timsStep，initialValue，coordnate） 计算

17. Export（"luaResult.dat"，0）导出计算结果

温度场计算的解析解和使用上述Lua脚本求解得到结果对比见图4。由此可见，计算结果误差较小，说明本文有限元计算程序能够求解得到合理的数值解。

C++程序也可以通过Lua/C API调用Lua脚本中预定义的函数，图4温度场左侧的边界条件定义如下。

1. function LuaFunc_BC_left（x， y） 左侧边的值

2.   return 10*sin（3.1415926*x/50）

3. end

4. addBC（1，0，0，"LuaFunc_BCleft"） 左側边的边界条件 #01

通过调用Lua脚本中边界条件设定的函数，完成边界条件设置，但应当避免每次迭代过程都调用Lua脚本，以保证计算速度。

3.2 蓄热砖温度场分析

结合在C++中设定的且可在Lua脚本中被调用的函数，编写蓄热砖温度场求解脚本，求解步骤如下：（1）定义下底边的热流边界条件和其他边的绝热边界条件;（2）定义蓄热砖材料的热物性参数;（3）定义蓄热砖的4个顶点;（4）定义蓄热砖计算域和4个边的边界条件，定义蓄热砖内的孔道（这些孔道要在计算域中去除，每个孔道需要定义节点、弧线段并设置绝热边界条件）;（5）定义计算域及其材料，设定网格划分最大面积阈值;（6）求解代数方程;（7）输出计算结果。具体代码如下。

1. print（"Step1： 定义边界条件"）

2. addBC（2，2500，0，""）热流边界条件 #01

3. addBC（2，0，0，""）绝热边界条件 #02

4. print（"Step2： 定义材料"）

5. addMaterial（5，3000，1000，""）氧化镁热物性

6. print（"Step3： 定义节点"）

7. addNode（0，0）Node #00 左下节点

8. addNode（0.4，0）Node #01 右下节点

9. addNode（0.4，0.2）Node #02 右上节点

10. addNode（0，0.2）Node #03 左上节点

11. 孔道建模

12. nodeID，r，dis，x0，y0=4，0.014，0.045，0.04，0.035孔道半径、间距等

13. for j=0，3，1 do垂直方向4行孔道

14.   for i=0，7，1 do水平方向8列孔道

15.   addNode（x0+i*disr，y0+j*dis）孔道直徑节点1

16.    addNode（x0+i*dis+r，y0+j*dis）孔道直径节点2

17.    print（"Step4.1：添加弧线段"）

18.    addArcSgmt（nodeID，nodeID+1，180，15，2）孔道上弧段，剖分15段，采用#2绝热条件

19.    addArcSgmt（nodeID+1，nodeID，180，15，2）孔道下弧段，剖分15段，采用#2绝热条件

20.    print（"Step4.2： 定义计算域内的孔道"）

21.    addHole（x0+i*dis，y0+j*dis）设定孔洞区域

22.    nodeID=nodeID+2

23.   end

24. end

25. print（"Step4.3：Add 蓄热砖4条边"）

26. addLineSgmt（0，1，60，1）;下底边，剖分60段，边界条件#01 热流边界条件

27. addLineSgmt（1，2，30，2）右侧边，剖分30段，边界条件#02 绝热

28. addLineSgmt（2，3，60，2）上底边，剖分60段，边界条件#02 绝热

29. addLineSgmt（3，0，30，2）左侧边，剖分30段，边界条件#02 绝热

30. print（"Step5： 设定计算域及其材料，网格最大面积"）

31. materialID，maxAreaSize=1，0.00005

32. addDomain（0.001，001，materialID，maxAreaSize）计算域材料为前述定义#01

33. print（"Step6： 求解"）

34. iterations，timsStep，initialValue，coordnate=60*60*10，1，20，0迭代次数，时间步长，初始值

35. Solve（iterations，timsStep，initialValue，coordnate）

36. print（"—Step7： 导出计算结果"）

37. Export（"luaResult.dat"，0）

38. print（"Soulution Done！"）

使用上述Lua脚本生成的蓄热砖网格见图5，共计2 931个节点、4 784个三角形单元。蓄热砖宽面被剖分为60段，窄面被剖分为30段，孔道被剖分为30段。通过Lua语句的两重循环，实现孔道几何尺寸设定、孔道布置、孔道网格分段数设定和孔道边界条件的设定，可极大简化有限元分析的前处理过程。如果使用常规商业有限元分析软件建模，每个孔洞设置一次边界条件，则需要设定32次边界条件，而通过Lua脚本批量建模并设定边界条件，前处理操作时间明显缩短。

使用电阻丝加热蓄热砖10 h后，其温度场的计算结果见图6。蓄热砖左右对称，边界条件也对称，因此温度场也呈现左右对称特点。下底面（热面）为热流边界条件，其温度分布最高，上底面（冷面）温度分布最低。蓄热砖温度随高度增加呈非线性减小;越靠近热面，温度场变化越剧烈。孔道附近温度场变化相对剧烈，但孔道附近的等温线都与孔道正交，这是因为孔道为绝热边界条件，所以无热流通过。

如果需要改变蓄热砖孔道直径、排列间距等几何特征参数，只需要修改Lua脚本中的参数即可，无须重新手工建模和设定边界条件，便于对计算进行参数化分析。

分别绘制图6中A点（蓄热砖最底部两个相邻孔道中心）、B点（蓄热砖几何中心）和C点（蓄热砖上部两个相邻孔道中心）的温度变化曲线，见图7。加热2 h后，3个点的温度均呈线性增加。由于C点距电阻丝最远，其温度在加热早期（2 h内）升温缓慢;A点距电阻丝较近，能快速升温;B点到A点和到C点的距离相近，但B点温度并非A点与C点温度的平均值，说明蓄热砖加热过程是非稳态导热。

4 结束语

探究使用Lua脚本简化有限元前处理建模过程，得到如下结论。

（1）使用C++开发二维温度场有限元分析程序，计算结果与解析解吻合较好，说明建立的有限元分析程序算法准确。

（2）在蓄热砖温度场有限元分析过程中，通过Lua/C API编写Lua脚本可简化有限元前处理过程，便于对有限元计算结果进行参数化分析。

参考文献：

[1]

陆艮峰， 张蓉， 张赛桥. Lua在轨道交通综合监控系统模拟器中的应用[J]. 工业控制计算机， 2017， 30（3）： 1315. DOI： 10.3969/j.issn.1001182X.2017.03.006.

[2] 陈佳铭， 王风立， 邓君湘， 等. Lua脚本与C++交互流程及在其HSTPN仿真软件的应用[J]. 计算机应用与软件， 2018， 35（10）：1316. DOI： 10.3969/j.issn.1000386x.2018.10.003.

[3] 陆乔. 基于Lua的iOS动态化系统的设计与实现[D]. 武汉： 华中科技大学， 2019.

[4] 程君. 基于Lua的移动互联网中间件系统的研究与实现[D]. 南京： 东南大学， 2017.

[5] 宋宏江， 高何， 卢成志， 等. 一种基于Lua脚本的航天器遥控快速测试验证技术[J]. 航天器工程， 2020， 29（3）： 182186. DOI： 10.3969/j.issn.16738748.2020.03.028.

[6] 赵頔， 王启民. 基于ANSYS分析的蓄热砖蓄热特性数值模拟及实验研究[J]. 沈阳工程学院学报（自然科学版）， 2020， 16（2）： 3438. DOI： 10.13888/j.cnki.jsie（ns）.2020.02.008.

[7] 徐德玺， 金映丽， 邢作霞， 等. 基于有限元的固体电蓄热装置蓄热模拟及实验[J]. 机械工程与自动化， 2016（4）： 2325. DOI： 10.3969/j.issn.16726413.2016.04.009.

[8] 胡思科， 刘建宇， 邢姣娇. 具有圆、方孔道的固体蓄、放热特性的分析与比较[J]. 流体机械， 2015， 43（9）： 7378. DOI： 10.3969/j.issn.10050329.2015.09.015.

[9] 李晶晶， 李永光， 王治源， 等. 固体蓄热装置圆形和椭圆形孔自然对流放热特性的研究[J]. 上海电力学院学报， 2019， 35（6）： 525530. DOI： 10.3969/j.issn.10064729.2019.06.003.

[10] 梁昆淼. 数学物理方法[M]. 4版. 北京： 高等教育出版社， 2009： 143162.

（编辑 武曉英）