基于稳定节点光滑有限元法的纯电动汽车电磁场仿真

郭志斌 黄湛勇 王中虎 王刚

摘要：   针对纯电动汽车电磁场数值分析时传统有限元法（finite element method， FEM）因数值“过硬”而计算精度低的问题，在传统FEM的基础上引入梯度光滑技术和稳定项修正，采用基于稳定节点的光滑有限元法（stable nodebased smoothed FEM， SNSFEM）对长直接地金属槽和纯电动汽车整车电磁场算例进行仿真分析。结果表明，SNSFEM可显著降低前处理网格划分难度，在一定程度上软化数值模型，具有计算效率高、精度高、收敛速度快和抗网格畸变能力强等优点，在工业应用中具有较大潜力。

关键词：

纯电动汽车; 稳定节点; 积分算法; 梯度光滑; 电磁场; 有限元

中图分类号：  TB115.1; TM153.1

文獻标志码：  B

Electromagnetic field simulation of pure electric vehicle based

on stable nodebased smoothed finite element method

GUO Zhibin， HUANG Zhanyong， WANG Zhonghu， WANG Gang

（School of Mechanical Engineering， Hebei University of Technology， Tianjin 300401， China;

Tianjin Key Laboratory of Power Transmission and Safety Technology for New Energy Vehicles， Tianjin 300130， China）

Abstract：

The numerical value is "overlystiff" in the traditional finite element method（FEM） for electromagnetic field numerical analysis of pure electric vehicle， which leads to its low precision. As to this issue， the gradient smoothing technique and the correction of stability term are employed based on the traditional FEM， the electromagnetic fields of long straight grounding metal slot and pure electric vehicle are simulated and analyzed by using stable nodebased smoothed FEM（SNSFEM）. The results show that the difficulty of mesh generation can be reduced using SNSFEM， and the numerical model is softened in a certain extent. The advantages of SNSFEM are high efficiency， high precision， fast convergence and strong ability to resist grid distortion. SNSFEM has great potential in industrial application.

Key words：

pure electric vehicle; stable node; integration method; gradient smoothing; electromagnetic field; finite element

0 引 言

电动汽车电磁场的数值分析，对于评估其电磁安全性具有重要意义。有限元法（finite element method， FEM）是电磁场数值计算中最常用的方法之一，广泛应用于电动汽车的电磁仿真中。[13]黄劭刚等[4]利用FEM研究发电机旋转磁场波形和电压波形;王春兰等[5]利用FEM研究电涡流传感器的电磁场问题，并验证计算结果的有效性。传统FEM可以解决大部分电磁场数值计算问题，但是也存在缺陷，离散网格的尺寸、插值函数的阶次等因素对算法精度影响很大。对于某些复杂的工程结构，FEM需要重复多次进行网格划分和加密操作，增加设计难度且降低计算效率。[6]针对传统FEM的缺点，边界元法（boundary element method， BEM）被提出。BEM只需对边界进行离散，在前处理阶段有较大优势，广泛应用于无界区域的电磁分析。[710]但是，使用边界积分方程离散得到的系数矩阵是满秩矩阵，因此BEM计算效率较低，难以解决大规模的实际工程问题。

近年来，针对电磁问题，专家学者提出多种新的方法，并取得较大进展。LIU等[11]在FEM中引入梯度光滑的概念，提出基于节点的光滑有限元法（nodebased smoothed FEM， NSFEM），可有效软化计算模型的刚度，显著提高数值解精度，数值分析的计算结果较好[1213]。但是，NSFEM模型“过软”，其不稳定性阻碍其在复杂工程中的应用。[14]FENG等[15]和WANG等[16]将应变梯度项引入能量方程，进一步提出基于稳定节点的光滑有限元法（stable nodebased smoothed FEM， SNSFEM），可用于模拟电磁成形和电磁铆接过程[1720]。通过添加稳定项进行修正，NSFEM的稳定性得到有效改善，并可获得理想的系统刚度。CUI等[17]验证SNSFEM具有较高的计算精度并且可以消除NSFEM解的不稳定性缺陷。基于上述研究工作，本文建立纯电动汽车电磁场分析数值模型，推导利用SNSFEM求解纯电动汽车电磁场的基本公式。利用SNSFEM分析长直接地金属槽模型和纯电动汽车整车电磁场模型，验证其可靠性，结果表明：与FEM相比，SNSFEM计算精度更高、收敛性更好，可有效地用于工程电磁场的仿真分析。

1 电磁场基本方程

在二维静态电磁域中，对于任意形状封闭的域Ω，场函数Φ（x）（x=[x y]T）应满足

与标准伽辽金弱形式相比，SNSFEM对电磁刚度矩阵进行光滑处理，下面对电磁问题的SNSFEM方案进行推导。

3 SNSFEM的离散形式

3.1 构造光滑域

采用SNSFEM求解问题时，插值在单元内进行，而积分基于重新构建的光滑域。二维问题中光滑域的构造方式分两步：首先，将分析域离散为3节点三角形网格，节点总数为Nn，单元总数为Ne;然后，基于三角形网格各节点进一步形成光滑域。二维问题中基于节点k的光滑域示意见图1。节点k与相连的三角形形心和各边中点顺次连接形成各节点的光滑域，因此该光滑域满足条件

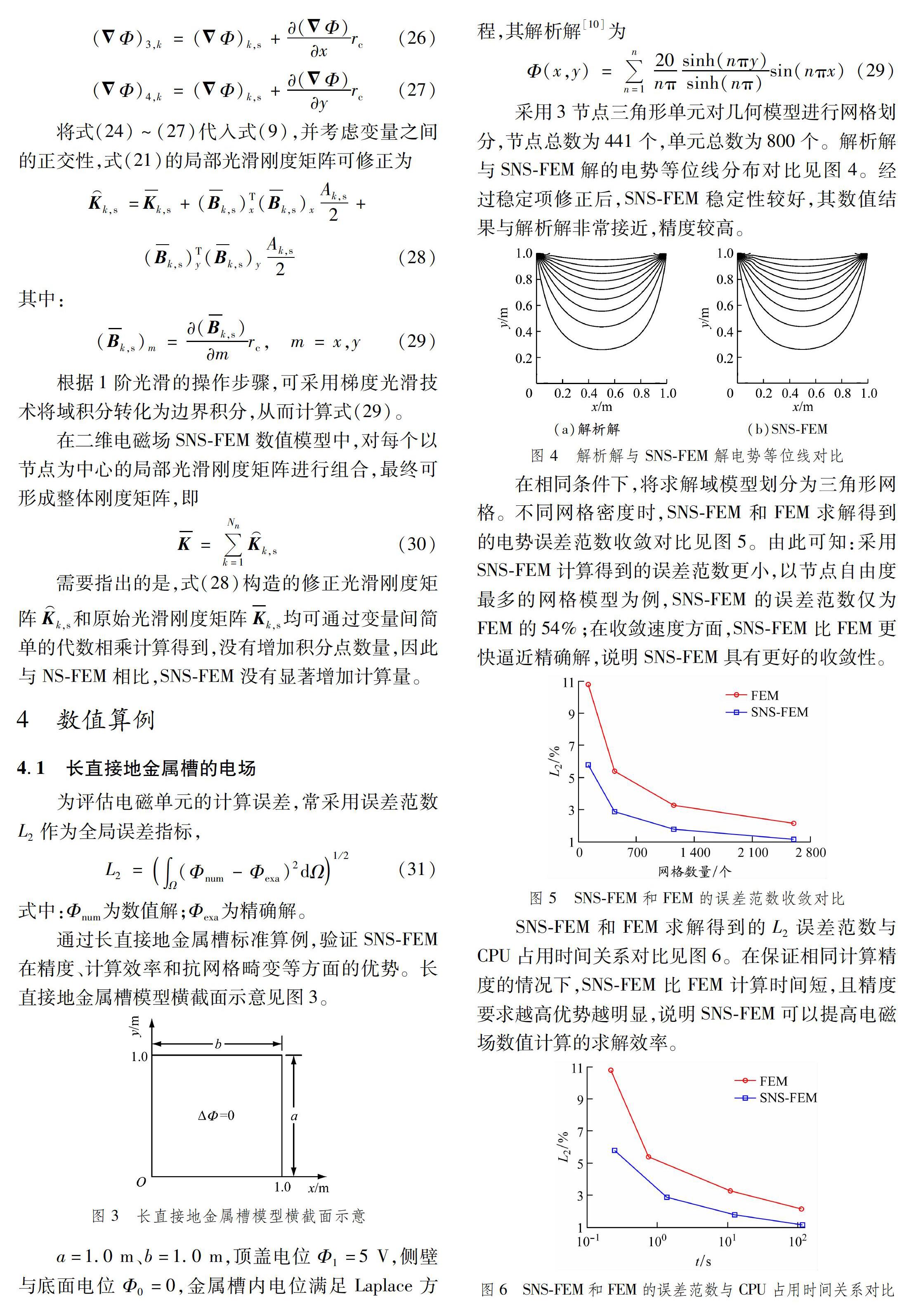
在相同条件下，将求解域模型划分为三角形网格。不同网格密度时，SNSFEM和FEM求解得到的电势误差范数收敛对比见图5。由此可知：采用SNSFEM计算得到的误差范数更小，以节点自由度最多的网格模型为例，SNSFEM的误差范数仅为FEM的54%;在收敛速度方面，SNSFEM比FEM更快逼近精确解，说明SNSFEM具有更好的收敛性。

SNSFEM和FEM求解得到的L2误差范数与CPU占用时间关系对比见图6。在保证相同计算精度的情况下，SNSFEM比FEM计算时间短，且精度要求越高优势越明显，说明SNSFEM可以提高电磁场数值计算的求解效率。

为测试SNSFEM的抗网格畸变能力，对图4的网格模型进行畸变处理，产生非均匀分布节点坐标的表达式为

式中：Δx和Δy分别为初始均匀分布节点在x和y方向的节点间距;r为计算机在-1.0～1.0范围内产生的随机数;αir为畸变因子，取值范围为0～0.5，αir越大则网格畸变越严重。αir=0（正常网格）和αir=0.5（畸变网格）的误差范数对比见图7。FEM受网格畸变的影响较大，误差范数明显上升，而SNSFEM计算结果几乎不受网格畸变影响。在实际工程中，利用规则网格离散问题域的可能性较小，因此SNSFEM具有更高的工程应用价值。

4.2 纯电动汽车的磁场分布

将纯电动汽车作为研究对象，验证SNSFEM在实际工程中的高效性。在汽车电磁场分析中，电机和电池系统均影响车内腔体的电磁环境，因此必须研究具有多个磁场发生源的汽车车内复杂电磁场分布。电动汽车的形状和内部结构复杂，电磁场计算时可将整车模型简化为二维平面模型，只研究动力电池和电机对整车电磁场的影响。

当网格节点数相同时，SNSFEM和FEM计算得到的汽车车内腔体的磁势分布云图分别见图9（a）和9（b）。因为无解析解，所以采用节点间距极小（节点数7 234个）时的有限元解作为参考解，见图9（c）。由此可知：FEM的数值解与参考解偏差较大，且在前部电机周围表现明显;SNSFEM得到的数值解与参考解吻合度较高，误差较小。

SNSFEM的计算结果比FEM结果更接近参考解，SNSFEM计算的磁勢分布与参考解吻合，而FEM结果有一定偏差。SNSFEM在分析纯电动汽车复杂电磁问题时具有较高的精度，说明SNSFEM更适用于工程计算。

5 结 论

基于SNSFEM建立纯电动汽车电磁场分析数学模型，研究纯电动汽车的电磁场分布，通过数值算例验证SNSFEM可靠性，结论如下。

（1）SNSFEM采用三角形单元对问题域进行离散，可显著降低网格划分难度。

（2）梯度光滑技术和稳定项修正使SNSFEM具有与真实模型更相近的刚度。在相同单元条件下，SNSFEM的精度明显优于FEM。

（3）与传统FEM相比，SNSFEM具有计算效率高、收敛速度快和抗网格畸变能力强等优点。

（4）对于边界复杂的纯电动汽车电磁场问题，SNSFEM的计算结果比FEM的计算结果更精确，因此SNSFEM在工业应用中具有较大潜力。

参考文献：

[1]JIN J M. Finite element method in electromagnetics[M]. 3rd ed. New Jersey： Wiley IEEE Press， 2014： 59.

[2] 张景明， 黄劭刚， 陈瑛. 同步发电机负载时二维电磁场有限元分析[J]. 微特电机， 2005， 33（6）： 910. DOI： 10.3969/j.issn.10047018.2005.06.002.

[3] 姜峰， 张建峰， 贾洪仁， 等. AC接触器电磁场有限元分析[J]. 计算机辅助工程， 2010， 19（2）： 8790. DOI： 10.3969/j.issn.10060871.2010.02.020.

[4] 黄劭刚， 夏永洪， 张景明. 基于ANSYS软件的电机电磁场有限元分析[J]. 微特电机， 2004， 32（5）： 1214. DOI： 10.3969/j.issn.10047018.2004.05.003.

[5] 王春兰， 张钢， 董鲁宁， 等. 电涡流传感器的有限元仿真研究与分析[J]. 传感器与微系统， 2006， 25（2）： 4143. DOI： 10.3969/j.issn.10009787.2006.02.014.

[6] 张勇. 计算电磁学的无单元方法研究[D]. 武汉： 华中科技大学， 2006. DOI： 10.7666/d.d048580.

[7] DRANDIC' A， TRKULJA B. Computation of electric field inside substations with boundary element methods and adaptive cross approximation[J]. Engineering Analysis with Boundary Elements， 2018， 91： 16. DOI： 10.1016/j.enganabound.2018.03.002.

[8] PARREIRA G F， SILVA E J， FONSECA A R， et al. Elementfree Galerkin method in threedimensional electromagnetic problems[J]. IEEE Transactions on Magnetics， 2006， 42（4）： 711714. DOI： 10.1109/TMAG.2006.872014.

[9] SIMPSON R N， LIU Z， VZQUEZ R， et al. An isogeometric boundary element method for electromagnetic scattering with compatible Bspline discretizations[J]. Journal of Computational Physics， 2018， 362： 264289. DOI： 10.1016/j.jcp.2018.01.025.

[10] 聂昕， 李永利， 何智成. 基于一种新型数值算法的电磁场仿真研究[J]. 机械强度， 2018， 40（2）： 378383. DOI： 10.16579/j.issn.1001.9669.2018.02.020.

[11] LIU G R， NGUYENTHOI T， NGUYENXUAN H， et al. A nodebased smoothed finite element method （NSFEM） for upper bound solutions to solid mechanics problems[J]. Computers & Structures， 2009， 87（1/2）： 1426. DOI： 10.1016/j.compstruc.2008.09.003.

[12] NGUYENTHOI T， LIU G R， NGUYENXUAN H， et al. Adaptive analysis using nodebased smoothed finite element method （NSFEM）[J]. International Journal for Numerical Methods in Biomedical Engineering， 2011， 27（2）： 198218. DOI： 10.1002/cnm.1291.

[13] LIU G R， CHEN L， NGUYENTHOI T， et al. A novel singular nodebased smoothed finite element method （NSFEM） for upper bound solutions of fracture problems[J]. International Journal for Numerical Methods in Engineering， 2010， 83（11）： 14661497. DOI： 10.1002/nme.2868.

[14] WANG G， CUI X Y， LI G Y. Temporal stabilization nodal integration method for static and dynamic analyses of ReissnerMindlin plates[J]. Computers & Structures， 2015， 152： 125141. DOI： 10.1016/j.compstruc.2015.02.007.

[15] FENG H， CUI X Y， LI G Y. A stable nodal integration method with strain gradient for static and dynamic analysis of solid mechanics[J]. Engineering Analysis with Boundary Elements， 2016， 62： 7892. DOI： 10.1016/j.enganabound.2015.10.001.

[16] WANG G， CUI X Y， FENG H， et al. A stable nodebased smoothed finite element method for acoustic problems[J]. Computer Methods in Applied Mechanics and Engineering， 2015， 297： 348370. DOI： 10.1016/j.cma.2015.09.005.

[17] CUI X Y， LI S， FENG H， et al. A triangular prism solid and shell interactive mapping element for electromagnetic sheet metal forming process[J]. Journal of Computational Physics， 2017， 336： 192211. DOI： 10.1016/j.jcp.2017.02.014.

[18] FENG H， CUI X Y， LI G Y. Coupledfield simulation of electromagnetic tube forming process using a stable nodal integration method[J]. International Journal of Mechanical Sciences， 2017， 128/129： 332344. DOI： 10.1016/j.ijmecsci.2017.05.003.

[19] LI S， CUI X Y， LI G Y. Multiphysics analysis of electromagnetic forming process using an edgebased smoothed finite element method[J]. International Journal of Mechanical Sciences， 2017， 134： 244252. DOI： 10.1016/j.ijmecsci.2017.10.018.

[20] LI S， CUI X Y， LI G Y. Modelling and demonstration of electromagnetically assisted stamping system using an interactive mapping method[J]. International Journal of Mechanical Sciences， 2018， 144： 312323. DOI： 10.1016/j.ijmecsci.2018.06.003.

（編辑 章梦）