基于自适应反步滑模的水面无人艇集群控制
2020-01-10胡建章唐国元王建军解德
胡建章,唐国元,王建军,解德
华中科技大学船舶与海洋工程学院,湖北武汉430074
0 引 言
协调有序的大规模群体行为在自然界中十分常见,如蚁群、鱼群、鸟群等,虽然这些群体中的个体行为简单、能力有限,但当它们一起协同工作时,却能够完成非常复杂的任务。人类通过模仿自然界中的群体行为,提出了无人集群的概念。其中,水面无人艇集群(USVs)作为一种无人海洋智能运载平台,在军事和民用领域具有极其广泛的应用前景,如反潜、反鱼雷、情报监视与侦察,以及海洋环境监测、海洋气象预报等[1-3]。并且无人艇及其集群具有在海—空界面间运行的优势,可作为水下自主潜航器与空中无人机之间的通讯中继站,从而充当立体化海洋空间的关键节点。
近年来,USVs 控制问题已经成为控制领域的研究热点,引起了很多学者的关注,同时也涌现出了大量的研究成果[4-8]。根据控制策略的不同,主要有领航者—跟随者法、基于行为法、人工势场法和虚拟结构法等。丁磊等[9]运用领航者—跟随者方法,建立无人艇集群数学模型,并设计反步控制器,使无人艇集群能够按照期望队形航行。宋艳荣等[10]使用人工势场法,同时考虑无人艇集群避碰和队形实现2 个问题,利用Multi-agent 理论,研究了基于势函数的集群队形控制问题。Monteiro等[11]采用基于行为的集群控制方法,解决了非线性系统的实时避障问题,得到了理想的集群运动轨迹。赵园等[12]将虚拟结构法与人工势场法相结合,在势函数中加入了相对碰撞函数,实现了无人艇集群协同避碰与避障问题。以上方法中,领航者—跟随者法严重依赖领导者状态,集群系统鲁棒性不足;基于行为法难以用精确的数学方法进行分析并确保集群的稳定性;人工势场法存在局部最优解的问题,构造合适的势函数较为困难。
本文将基于虚拟结构法的控制策略,建立各艘无人艇与虚拟结构对应点之间的位姿跟踪误差动态模型,将集群控制简化成跟踪误差的镇定控制。通过在控制器中加入虚拟结构的几何参数,改变无人艇集群的队形,以增强系统的灵活性。将控制器设计分为运动学与动力学2 个部分,针对系统自身的不确定性以及外界环境干扰等因素,基于李雅普诺夫稳定理论,设计自适应干扰观测器,并在控制器中进行补偿,实现欠驱动USVs的自适应反步滑模控制。
1 控制问题描述
1.1 无人艇数学模型
对于大多数无人艇的运动控制问题(如航向控制、航迹控制)而言,主要考虑其水平面的三自由度运动,单艘欠驱动无人艇水平面运动的非线性数学模型可表示为[10]


1.2 控制策略
本文采用基于虚拟结构法的集群控制策略来实现USVs 控制,其控制流程图如图1 所示。根据集群作业任务,设计虚拟结构,并定义虚拟结构的运动行为;控制各艘无人艇跟踪虚拟结构中的固定参考点,实现集群的队形保持;通过变换虚拟结构的几何形状,进行相应的集群队形变换,以适应各种集群任务需求。

图1 USVs 控制策略流程图Fig.1 Flow chart of control strategy for USVs
图2 为USVs 队形结构与跟踪误差图,图中O-xy为大地坐标系,o-uv为随体坐标系。设计虚拟刚体结构,选取结构中的任意一点为参考点,让该参考点按照期望轨迹Ω( )xd,yd运动。结构中其它点的位姿均可用相对于参考点的距离l 以及角度θ来表示:

式中:ηv=[xvyvψv]T,为虚拟结构中任意一点的位姿;ηd=[xdydψd]T,为参考点的位姿;R(ψd)为旋转矩阵;l=[lx ly0]T=[lcosθ lsinθ0]T。
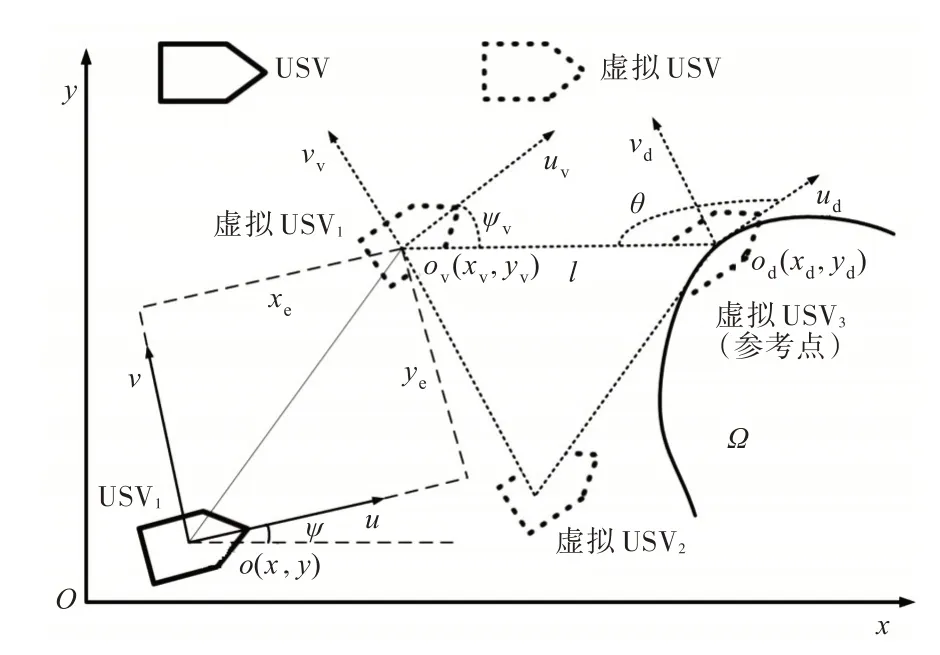
图2 USVs 队形结构与跟踪误差图Fig.2 Formation structure and tracking errors of USVs
把虚拟结构中的各点看作与各艘无人艇有着相似动力学特性的虚拟无人艇,仿照式(1)对其进行数学建模。由于虚拟无人艇没有驱动力及力矩,故其数学模型可表示为
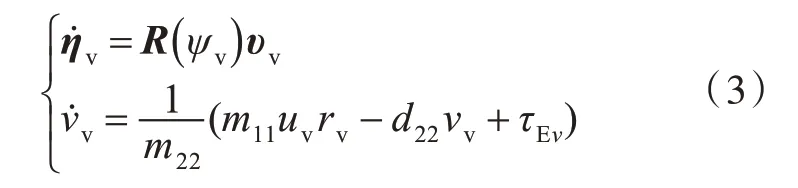
式 中:R(ψv)为 旋 转 矩 阵;υv=[uvvvrv]T=[ud-lyrdvd+lxrdrd]T,为虚拟无人艇的速度,其中ud,vd,rd为参考点的速度。
为了方便控制器的设计,将无人艇与虚拟无人艇之间的位姿跟踪误差从坐标系O-xy转换到坐标系o-uv中表示:
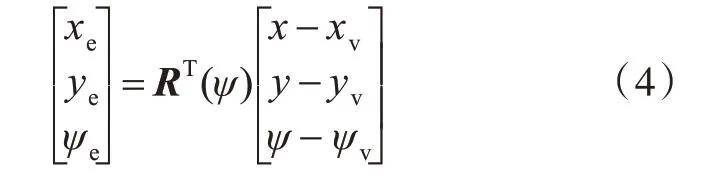
对式(4)左右两边求微分,并结合式(1)和式(3),可得位姿跟踪误差模型

式中:ve=v-vv;α=m11/m22;β=d22/m22。
因此,本文的欠驱动USVs 控制问题就简化成了式(5)的镇定控制问题。
1.3 控制目标
控制目标:对于由多艘欠驱动USV 组成的集群系统的控制问题,采用虚拟结构法的控制策略,设计控制率τu和τr,将集群系统的位姿跟踪误差镇定到原点附近足够小的范围,以实现无人艇的集群化运作。
根据控制目标,在设计控制器之前,先作如下假设:
假设1:不确定项τE有界,但其上界未知,即|τE|≤τEmax<∞。
假设2:只考虑各艘无人艇向前航行的情况,不考虑倒车,即u>0 且u> ||v。
2 控制器设计
2.1 运动学控制器设计
首先,进行运动学回路设计,将纵荡速度u看作子系统xe的输入,根据的表达式,设计uα为

式中:uα为u的虚拟控制量;k1为正常数。
为了简化问题,引入一个坐标变换ze=ye+ve/β,以消去ve项。对ze求导,并将式(6)代入:

取k1=β α,以消去xe项,则式(7)可化简为

将航向角偏差ψe看作ze子系统的输入,根据że的表达式,设计为

定义航向角偏差的误差量we=ψe-ψαe ,对we求导:

将艏摇角速度r看作we子系统的输入,设计rα:

式中:rα为r的虚拟控制量;k3为正常数。
2.2 动力学控制器设计
定义纵荡速度误差为ue=u-uα,选择滑模面su=ue,并对其求导:

采用指数趋近律ṡ=-λsgns-ks(λ>0,k>0):
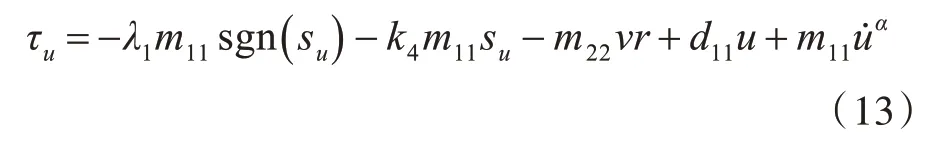
式中,λ1,k4为正常数。
同理,定义艏摇角速度误差量re=r-rα,选择滑模面sr=re,并对其求导:
同样采用指数趋近律:


式中,λ2,k5为正常数。
针对不确定干扰,设计自适应干扰观测器:

式中:ζu,ζr为辅助控制项;,分别为τEu,τEr的估计值;k6,k7为正常数。
则式(13)和式(15)可改写为:

至此,基于自适应反步滑模的欠驱动USVs 控制器式(18)~式(19)设计完毕。
3 稳定性分析
定理1:对于由多艘欠驱动USV 组成的集群系统的控制问题,在满足假设1 和假设2 的条件下,设计自适应反步滑模控制器式(18)~式(19),通过选择合适的控制参数ki(1 ≤i≤7),λj(1 ≤j≤2),使集群系统的位姿跟踪误差渐进收敛至原点附近一个足够小的邻域,即误差一致最终有界,从而实现USVs 的集群控制目标。
证明:
根据上一节设计的控制量,重新整理误差系统,可得



4 仿真试验
假设本文的自适应反步滑模控制律式(18)~式(19)为控制律1,普通反步滑模控制律式(13)和式(15)为控制律2。现针对本课题组由3 艘相同欠驱动USV 组成的集群,分别采用控制律1 和2进行仿真试验,并对比试验结果,以验证本文控制方法的正确性和有效性。
无人艇总长4.68 m,型宽1.70 m,型深0.55 m,吃水深0.40 m,艇体质量538 kg。无人艇的建模参数为:m11=646 kg,m22=837 kg,m33=155kg ⋅m2,d11=303 kg/s,d22=425 kg/s ,d33=74 (kg ⋅m2)/s 。假设存在10%的建模误差,在仿真试验中考虑极端情况,将无人艇的模型参数取为:1.1m11,0.9m22,0.9m33,0.9d11,1.1d22,1.1d33。
假设时变的外界干扰为

给定集群中3 艘USV 的初始状态分别为:

选择控制器参数:k1=β α=0.66,k2=0.10,k3=k4=k5=k6=k7=1.10,λ1=λ2=0.20 。 其 中,α=m11m22=0.94,β=d22m22=0.62。
仿真试验的具体流程如下:
1)在初始的50 s,设定无人艇集群的期望队形为“一”字形,即l1=0,θ1=0,l2=20,θ2=π 2,l3=20,θ3= -π 2 ,期望航迹为与x 轴重合的直线,期望的航行速度为ud=2 m/s;
2)接下来的50 s,保持航迹不变,将集群的期望航速降为ud=1 m/s,同时将队形变换为“品”字形,即l1=0,θ1=0,l2=10,θ2=2π 3,l3=10 ,θ3=-2π 3;
3)之后的300 s,保持队形与航速不变,无人艇集群按照S 形曲线航迹行驶。
图3 和图4 分别为采用控制律1 和控制律2 的无人艇集群航迹仿真结果。3 艘无人艇从初始的零散状态迅速集结成“一”字型编队;在50 s 时刻(x≈100 m),集群降低航速,收拢队形,并变换成“品”字形编队;在100 s(x≈150 m)时刻,集群保持“品”字形编队,按照S 形曲线航迹行驶。可明显看出,相较于控制律2,在控制律1 的作用下,整个航行过程无人艇集结迅速,编队航行稳定,队形变换流畅,集群控制效果显著,展现出了较强的灵活性。

图3 无人艇集群航迹图(控制律1)Fig.3 Formation trajectorys of USVs(control law 1)
图5 和图6 分别为采用控制律1 和控制律2 的3 艘无人艇的航行速度。从中可看出,纵荡速度最终保持在1 m/s 左右,由于存在曲线航迹,横荡速度与艏摇角速度也都不为0。
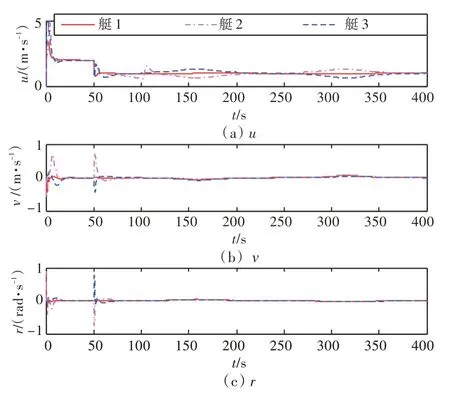
图5 无人艇航行速度(控制律1)Fig.5 Velocities of USVs(control law 1)

图6 无人艇航行速度(控制律2)Fig.6 Velocities of USVs(control law 2)
图7 和图8 分别为采用控制律1 和控制律2 的3 艘无人艇的控制输入。从中可看出,输入曲线平滑,抖振较小,能够有效减少推进器的机械损耗。
图9 和图10 分别为采用控制律1 和控制律2的3 艘无人艇的跟踪误差。可以看出,在控制律1的作用下,无人艇的跟踪误差一致收敛到了原点附近较小的邻域,并且收敛迅速,基本无超调。表明本文控制律对于不确定外扰具有良好的补偿能力,具有较强的鲁棒性。而控制律2 的航行误差则较大,不满足控制精度要求,从而进一步验证了本文控制方法的可行性与优越性。
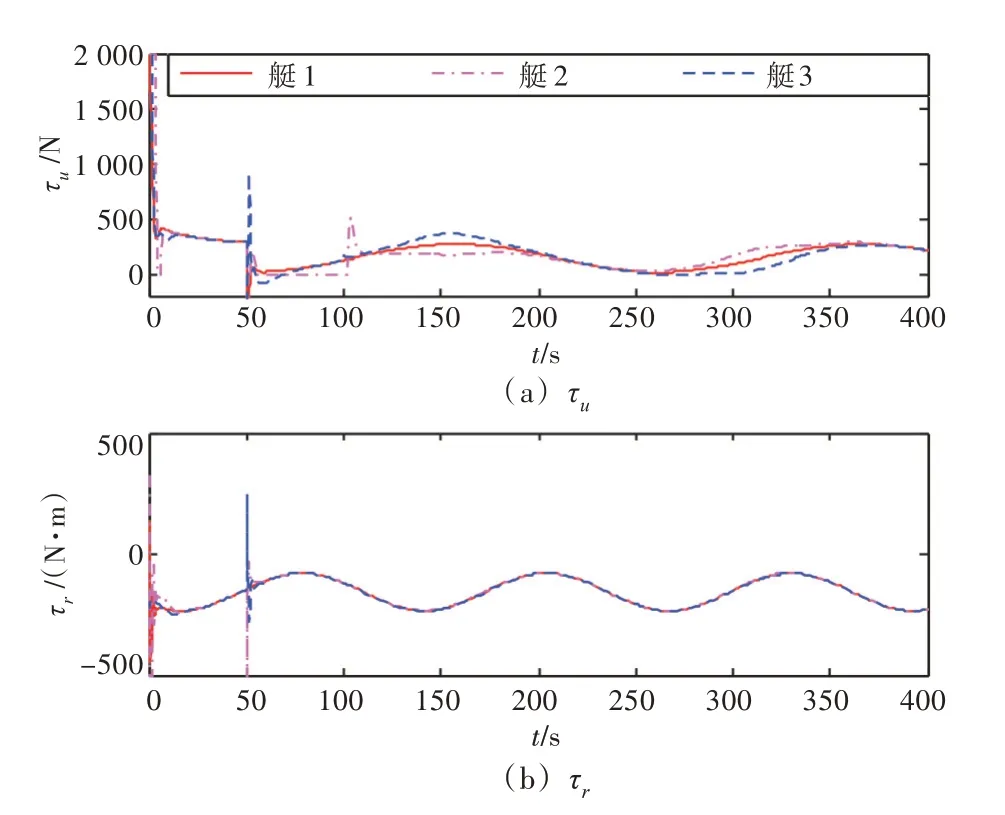
图7 无人艇控制输入(控制律1)Fig.7 Control inputs of USVs(control law 1)
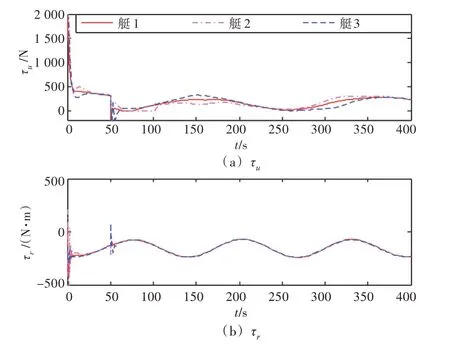
图8 无人艇控制输入(控制律2)Fig.8 Control inputs of USVs(control law 2)
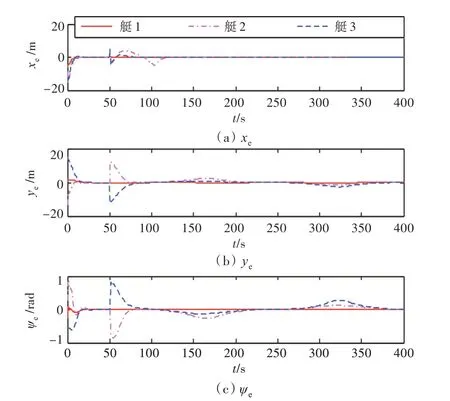
图9 无人艇跟踪误差(控制律1)Fig.9 Tracking errors of USVs(control law 1)

图10 无人艇跟踪误差(控制律2)Fig.10 Tracking errors of USVs(control law 2)
5 结 语
本文采用虚拟结构法的集群控制策略,从运动学和动力学2 个方面出发,结合反步法、滑模变结构控制以及李雅普诺夫稳定等非线性理论,对欠驱动USVs 控制问题展开了研究。充分考虑系统不确定性和外界环境干扰的影响,设计了USVs的自适应反步滑模控制器,并证明了闭环系统的稳定性。仿真对比试验验证了本文控制方法的可行性与优越性,具体表现在:无人艇集群运作效果良好,集群队形变换流畅,且能够对各种不确定干扰进行自适应补偿,展现出了较强的鲁棒性、灵活性与适应性,达到了预定控制目标。这为USVs 控制的实际应用提供了有效基础。
