多高超声速导弹协同末制导律及可行初始位置域研究
2020-01-10李东旭王晓芳
李东旭,王晓芳,林 海
(北京理工大学 宇航学院,北京 100081)
高超声速导弹因其飞行速度快、作战范围广等特点在近年来成为研究热点。与此同时,美国正在研制和部署全球一体化反导系统,单一高超声速导弹的突防能力受到严峻考验,多高超声速导弹通过各弹之间的战术、火力相互支援和协调,形成有掩护的攻击,更加符合未来战场的作战需要,是提升协同突防能力和攻击能力的有效手段[1]。因此对多高超声速导弹协同作战问题进行深入研究具有十分重要的意义。
高超声速导弹协同末制导技术是其协同作战的核心关键技术。关于协同末制导律,目前针对常速飞行的战术导弹的研究比较多,根据弹间是否存在通讯,可以分为具有指定攻击时间约束的末制导律[2-7]与存在弹间通讯的协同末制导律[8-9]。但高超声速导弹具有飞行速度时变且不可控的特点[10-15],文献[2-9]的方法并不适用。文献[11]针对速度非定常的导弹,将攻击时间控制问题转化为导弹实际剩余航程对标称剩余航程的跟踪问题,提出了2种分别满足攻击时间约束、攻击时间与攻击角度约束的导引律,但其只适用于导弹在二维平面内运动的情况。针对导弹在三维空间运动的情况,文献[12]提出了一种基于弹目距离的协同策略,根据当前时刻的速度及弹目距离计算侧向速度前置角,从而控制导弹侧向机动,实现了多高超声速导弹对目标的协同打击。文献[13]基于每个时刻的状态在线对剩余飞行时间进行估计,将其与给定攻击时间的误差作为反馈,实现对攻击时间的控制。为了提高对目标的攻击效能,通常对攻击落角有限制,而文献[12-13]只考虑了攻击时间的约束,并没考虑攻击角度的约束。另外,由于各导弹的速度、机动性都是有限的,因此,其并不是从任何位置开始末制导都可以实现协同攻击的,此时,需对导弹可行的末制导初始位置域进行研究,而上述文献均没有涉及这一点,故而针对多高超声速导弹协同作战问题,设计能够同时满足攻击时间和攻击角度约束的三维协同制导律以及对各导弹的可行末制导初始位置域进行研究是非常重要和必要的。
本文考虑高超声速导弹速度时变且不可控的特点,在文献[13]的基础上进行进一步研究,通过纵向制导指令控制落角、侧向制导指令控制攻击时间,从而得到同时满足落角与攻击时间约束的协同末制导律。在此基础上,考虑各导弹的机动能力、末端速度约束,给出计算其攻击时间范围的方法和一维、二维可行末制导初始位置域的求解方法。最后通过仿真验证了协同末制导律的良好性能与可行域求解方法的有效性。
1 问题描述
在末制导段,假设导弹攻击静止目标,其在三维空间的相对运动关系如图1所示。
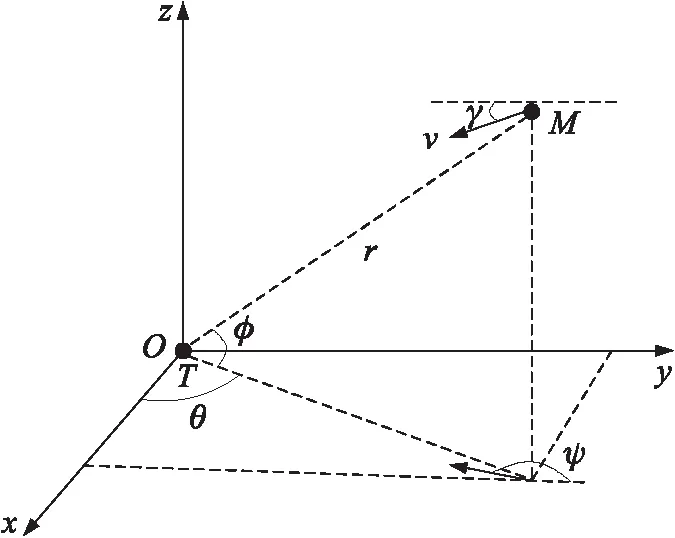
图1 导弹目标相对运动关系图
图1中,Oxyz为地面坐标系,M和T分别代表导弹和目标,r为弹目距离,φ和θ分别为俯仰、偏航方向视线角,图示方向为正。v、γ和ψ分别为导弹速度、弹道倾角和弹道偏角,图示γ方向为正,ψ方向为负。由图1可得弹目相对运动的方程组为

(1)
式中:η=θ+ψ+(π/2)为偏航方向速度前置角。
表征导弹运动非线性倾斜转弯模型[13]为
(2)
式中:FL、FD分别为导弹的升力与阻力,m为导弹质量,g为重力加速度,σ为导弹的倾侧角,由于采用BTT-90模式,有-90°≤σ≤90°,(x,y,z)为导弹位置。
多导弹要想在指定的时间td以指定的落角γ*对目标进行饱和攻击,须满足:
(x(td)y(td)z(td)γ(td))T=(0 0 0γ*)T
2 三维协同末制导律设计
高超声速导弹的速度时变且不可控,给多导弹协同末制导律的设计带来很大挑战。文献[13]通过预测值计算剩余飞行时间,将其与给定剩余攻击时间的差作为反馈得到制导指令,实现攻击时间控制。本文在此基础上,考虑攻击角度的约束,给出了能够同时实现攻击时间和攻击角度约束的末制导律。
对于高超声速导弹来讲,其剩余飞行时间的高精度估计是一个难题,采用数值计算的方法对其进行在线估计。具体过程为:



②为了得到剩余飞行时间预测值,建立性能指标函数为
(3)
采用梯度下降法[13]对式(3)所示的无约束优化问题进行求解,得到:
(4)

(5)
基于式(5)可对剩余飞行时间在线估计。
(6)
式中:γ*为理想落角,N1为比例系数,K>0为制导参数。则导弹在预测时采用三维制导律表达式为
(7)
不同于文献[13]中通过纵向弹道的调整实现攻击时间约束,本文通过在侧向制导指令中加入理想攻击时间与预测攻击时间的误差作为反馈项实现对攻击时间的控制,而在纵向采用式(6)所示的偏置比例导引律实现对攻击落角的控制。
考虑攻击时间约束,令攻击时间误差[13]:
(8)
式中:tr是为使导弹的指令较平滑而设计的理想攻击时间函数,其表达式为[13]
式中:t0为基于导弹初始状态采用常规比例导引律的攻击时间,tp为控制t0到td变化速度的时间参数。大量实证研究表明:令tp=2td/3可以消耗较小的控制能量[13]。
将式(8)所示的时间误差作为反馈项引入侧向比例导引律指令,有:
式中:N2为比例系数,ku为设计参数。则侧向攻击时间控制思路为:在每个制导周期,基于式(7)制导律对剩余飞行时间进行预测,将计算得到剩余飞行时间与理想剩余飞行时间的差et作为反馈项引入侧向制导,侧向制导指令作用于弹体,在下一制导周期,基于新的导弹位置、速度等状态再采用式(7)制导律对剩余飞行时间进行预测,同时继续通过et对导弹进行控制,如此进行,直至最终实现在理想攻击时间击中目标。
故而三维空间的同时具有攻击时间和攻击角度约束的制导律为
(9)
在Matlab环境中调用fmincon函数寻优得到攻角指令,有:
αd=arg min|FL-FLd|
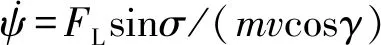
在本文中,假设实际攻角与倾侧角能够完全跟踪攻角指令与倾侧角指令,即:
3 末制导可行初始位置域研究
由于各导弹的机动能力有限,且通常对其末速有要求,因此,其并不是从任何位置开始末制导都能同时击中目标,实现协同,有必要在考虑导弹有限机动能力和末速约束的前提下研究各自在不同协同攻击时间对应的末制导可行初始位置域。当导弹滑翔至z0=h0的高度时转入末制导,且假设导弹初始速度大小和方向已确定。接下来选定合适的理想攻击时间,再在y=y0的前提下求解理想攻击时间对应的x方向一维可行位置域;最后求解x,y方向二维可行位置域。
3.1 攻击时间范围求解
当目标信息和末制导初期导弹的位置及速度已确定时,受可用过载和末速的约束,导弹能够实现的飞行时间是有限的,即存在最小攻击时间和最大攻击时间。
由于高超声速导弹速度时变且不可控,其攻击时间范围[tmin,tmax]无法采用解析方法进行求解,因此本文采用数值计算方法。当导弹采用式(7)所示带落角约束的三维比例导引律时,其攻击时间t0为最小攻击时间,即tmin=t0。在最小时间的基础上,令td=t0+iΔt(i=1,2,…,Δt为时间间隔)。从i=1开始计算td,此时通过仿真判断导弹采用式(9)所示的协同末制导律时是否满足可用过载n≤nmax及末速约束vf≥vfmin,如满足,则增加i,从而增大td进行再次仿真;如不满足,则输出上一步满足约束的td作为最大攻击时间tmax。由以上方法可求得在某个末制导初始位置下导弹的攻击时间范围。
3.2 一维可行位置域求解
首先求解一维可行位置域。假定导弹末制导初始位置y0、z0确定,选取合理的理想协同攻击时间td1,求解能以td1实现协同的x0的精确范围,即一维可行初始位置域。
研究导弹位于不同末制导初始位置时的协同可行性。假设两枚导弹A、B分别位于M1(x01A,y0,z0)和M2(x01B,y0,z0),且0
综上所述,对一维可行位置域的求解可以转化为求解最大攻击时间等于td1的x01A与最小攻击时间等于td1的x01B。以导弹x方向初始位置x0为设计变量,即:
X=x0
(10)
考虑导弹的可用过载与末速约束有:
(11)
式中:nmax为可用过载,vfmin为最小末速。
导弹实现协同的条件为以相同攻击时间td1击中目标,则性能指标函数可设为
minF1(X)=|t1-td1|
(12)
式中:t1为实际飞行时间。
式(10)~式(12)构成了优化模型,采用优化算法对其求解。在每次优化过程中,计算设计变量对应的攻击时间范围[t1jmin,t1jmax](j=1,2,…,p),令性能指标函数中t1=t1jmin,则优化计算得到x01max;令t1=t1jmax,则优化计算得到x01min。此时得到攻击时间td1所对应的一维末制导可行初始位置域[x01min,x01max]。改变期望协同攻击时间td1,可分别计算其对应的初始位置域。
3.3 二维可行位置域求解
仍然假设末制导初始时刻导弹的飞行高度z0=h0确定。考虑导引头的作用距离、开始末制导时的高度、导弹侧向机动能力等因素,设定x方向的初始位置范围[x02min,x02max],在此基础上,将二维可行域的求解问题转化为一维可行域的求解,即取x02k∈[x02min,x02max](k=1,2,…,q),基于3.2节的方法可求解导弹的初始x0=x02k,z0=h0时,对应于理想攻击时间td2的y方向坐标范围[y02kmin,y02kmax]。考虑在整个[x02min,x02max]范围内对应的[y02kmin,y02kmax],则可获得二维末制导可行初始位置域。
4 仿真与分析
4.1 协同末制导律性能分析
假设目标位于原点,导弹A和B的初始位置为M1(x0A,y0A,z0A)=(25 km,5 km,20 km),M2(x0B,y0B,z0B)=(28 km,-10 km,20 km)。两枚弹的初始速度均为v0=1 600 m/s,初始弹道倾角均为γ0=-10°,初始弹道偏角均为ψ0=-80°。升力系数CL和阻力系数CD[13]为
导弹的质量m=1 600 kg,参考面积S=0.502 6 m2。攻角允许范围为[-15°,15°]。式(7)、式(9)制导律中的N1=N2=3,κ=8×10-6,ku=10,K=-1.5。理想攻击时间td=30 s,理想落角γ*=-80°。仿真结果如图2~图7所示。

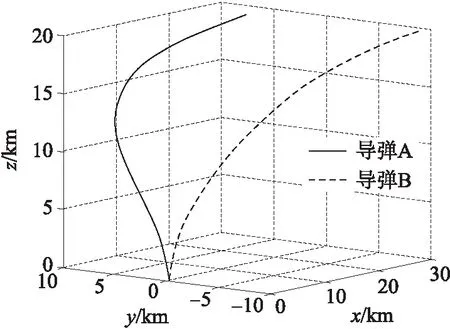
图2 两枚导弹弹道曲线

图3 两枚导弹弹道倾角变化曲线

图4 两枚导弹弹道偏角变化曲线

图5 两枚导弹攻角变化曲线
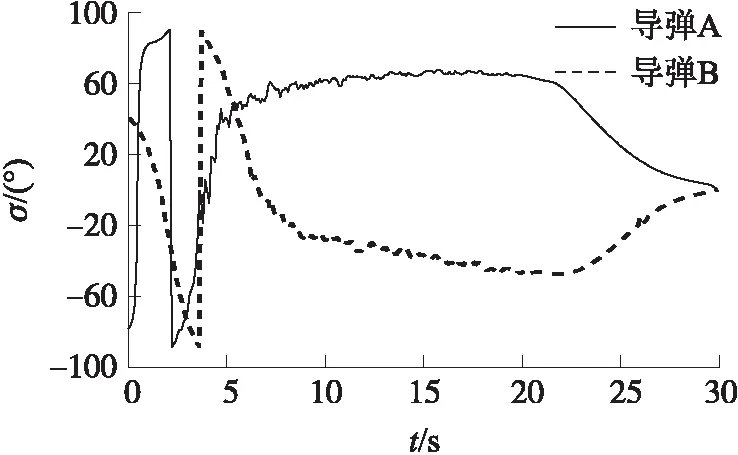
图6 两枚导弹倾侧角变化曲线

图7 两枚导弹et变化曲线
4.2 一维可行域仿真及分析
假设高超声速导弹滑翔至h0=20 km时转入末制导,令初始侧向坐标y0=0,分别设导弹C与导弹D的初始速度为v0C=1 600 m/s与v0D=1 500 m/s。其他初始条件与4.1中相同。为了研究方便,令理想攻击时间td1在[26 s,34 s]中每隔1 s取值。约束条件:vfmin==700 m/s,nmax=30。优化结果如表1与图8所示。
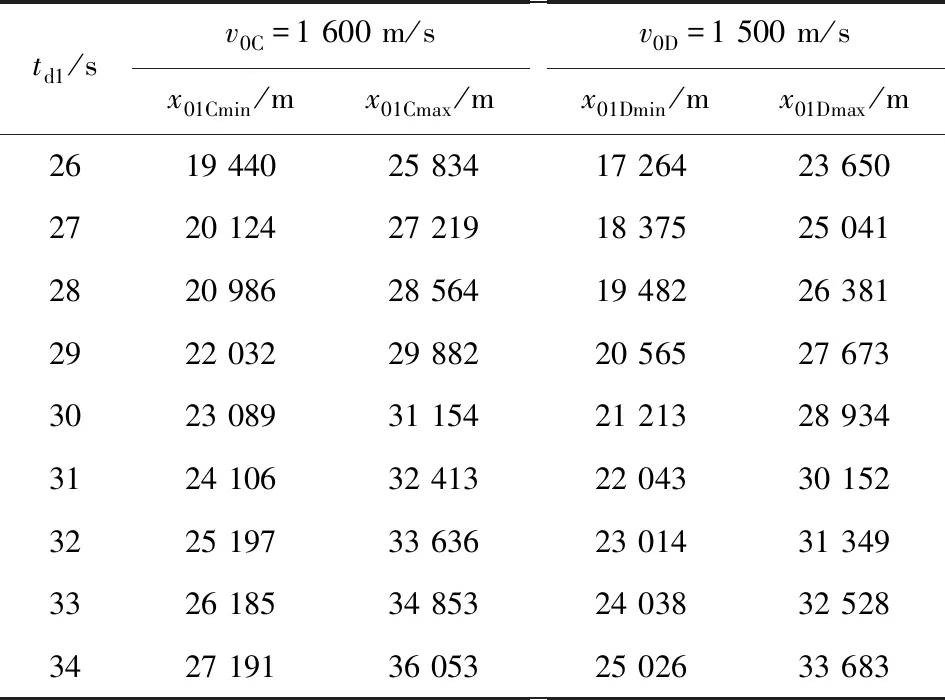
表1 一维协同可行初始位置域
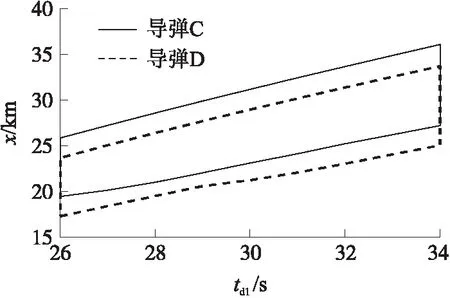
图8 两枚导弹一维可行初始位置域
由表1与图8可知,对应不同理想攻击时间,2个导弹均具有各自的可行初始位置域。由表1可知,由于导弹C的初速大于导弹D的初速,因此有x01Cmin>x01Dmin,x01Cmax>x01Dmax。由于导弹D初始速度较小,但其也必须满足末速要求,因此其初始位置域较小,如当td1=30 s时,导弹C可行位置域范围为8.065 km,导弹D只有7.721 km。另一方面,理想攻击时间越大,导弹可调整的范围越大,其可行初始位置域越大。
4.3 二维可行位置域仿真及分析
以导弹C为例,求解其二维可行位置域。同样假设其在高度为20 km处转入末制导。参考4.2节中求得的一维可行位置域,同时为了计算方便,设导弹C在x方向的初始坐标x02C∈[x02Cmin,x02Cmax]=[20 km,30 km]。令x02C在[x02Cmin,x02Cmax]中每隔1 km取值,其他初始条件与4.2中相同,求对应的侧向坐标范围。设定理想攻击时间td2分别为28 s、30 s和32 s,得到二维可行位置域如图9所示。
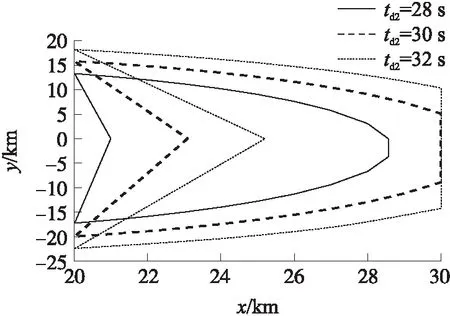
图9 不同td2时的二维可行初始位置域
当td2=28 s时,由表1可知,在y01C=0前提下,x01C范围为[20.986 km,28.564 km],当没有y02C=0的约束,求取二维可行初始位置域时,在20 km≤x02C<20.986 km也存在可行位置域,但是由图9可知此时可行的y02C是不连续的。较小的x02C对应的可行|y02C|较大,随着x02C的减小,可行y02C的范围减小,这是因为小的x02C和大的|y02C|对应着相差不大的初始距离,才有可能实现同一攻击时间。当20.986 km≤x02C≤28.564 km时,其对应着连续可行y02C,随着x02C的增大,可行y02C的范围减小,同样是因为相差不大的初始弹目距离才有可能达到相同的攻击时间。而当x02C>28.564 km时,初始弹目距离较大,导弹不做机动时的攻击时间已经大于理想攻击时间,故而无可行初始位置域。当td2=30 s和32 s时,与上述分析类似。
由表1可见,td2=28 s,30 s和32 s时,其一维可行初始位置域的交集为[25.197 km,28.564 km],在此范围内,同一x02C对应的y02C范围越大,这是因为理想攻击时间长,给导弹进行调节的时间和余地就大,因此,其可行初始位置域也大。
5 结束语
本文针对速度时变且不可控的多高超声速导弹,研究了能够使其在指定的时间以指定的落角对目标进行协同打击的三维末制导律。基于此末制导律,考虑多导弹各自的末制导初始速度大小及方向、可用过载约束和末速约束,提出了可实现协同飞行的各导弹的一维和二维的末制导可行初始位置域求解方法,并通过仿真进行了分析。相对于前人所做的工作,本文的贡献在于:
①针对高超声速导弹,基于纵向指令控制落角、侧向指令控制攻击时间的思路,对文献[13]进行改进,提出了同时具有攻击时间和攻击角度约束的三维协同末制导律。
②考虑各导弹的末制导初始速度大小及方向、机动能力和末速要求,提出求解其一维和二维的末制导可行初始位置域的方法。
本文的方法适用于多同构或异构速度时变且不可控的导弹协同飞行的情况,具有广阔的军事应用前景。
