城市暴雨强度公式理论频率曲线选择研究
2020-01-09肖友淦
肖友淦
(福州城建设计研究院有限公司 福建福州 350001)
0 引言
2013年3月25日,国务院正式发布了《国务院办公厅关于做好城市排水防涝设施建设工作的通知》(国办发〔2013〕23号),明确要求“各地区要结合气象、水文资料,对现有暴雨强度公式进行评价和修订”。在采用年多个样法编制城市暴雨强度公式时期,经验频率的计算和理论频率曲线的选择两大问题引发了学术界极大的争议。随着《室外排水设计规范》GB50014-2006(2016年版)(以下简称新版排水规范)的发布,要求新编暴雨强度公式采用年最大值法选样,并有如下规定:“选取的各历时降雨资料,应采用经验频率曲线或理论频率曲线加以调整,一般采用理论频率曲线,包括皮尔逊Ⅲ型分布曲线、耿贝尔分布曲线和指数分布曲线。根据确定的频率曲线,得出重现期、降雨强度和降雨历时三者的关系,即P、i、t关系值。”可以看出,新版排水规范用于暴雨强度公式参数拟合的降雨资料实际有4种情况:①采用经验频率曲线,对原始降雨资料进行目估适线;②采用皮尔逊Ⅲ型分布曲线调整过的降雨资料;③采用耿贝尔分布曲线调整过的降雨资料;④采用指数分布曲线调整过的降雨资料。本文将论述这4种方法的优劣,并提出最合适的频率分布曲线及其快速计算方法。
1 经验频率曲线
年最大值法时,经验频率(即年频率)计算公式一般采用[1-2]:
式中:P——年频率;
m——资料由大到小的序列;
N——资料年数。
表1为某城市1980年~2013年5min历时的降雨资料。假设该市暴雨强度公式的编制时间为2014年,那么,该市用于暴雨强度公式编制的5min历时降雨资料应为1980年~2013年(其中1999年、2000年无资料)资料,此时降雨经验频率和重现期如表2所示。假设该市暴雨强度公式的编制时间为2002年,那么,该市用于暴雨强度公式编制的5min历时降雨资料应为1980年~2001年(其中1999年、2000年无资料)资料,此时降雨经验频率和重现期如表3所示。两次暴雨强度公式编制时同一降雨量代表的重现期对比如图1所示。

表1 1980年~2013年5min历时降雨资料

表2 1980年~2013年5min历时降雨经验频率

表3 1980年~2001年5min历时降雨经验频率

图1 同一降雨量代表的重现期对比图
从图1可以看出,该方法与选用数据年限具有很大关系。如果在2002年暴雨强度公式编制时,直接采用经验频率曲线而不进行理论频率曲线修正,那么在高重现期时的降雨数据将偏大,低重现期时的降雨数据将偏小。例如,同样是20.3mm降雨,在2002年编制时为21年一遇降雨,在2014年编制时为33年一遇降雨,而2014年编制时的21年降雨重现期对应的雨量应介于19.3mm和20.3mm之间。
同时,采用经验频率曲线也难以进行频率曲线的外延。例如,利用30年的数据,预测重现期为100年的暴雨,这是不切实际的。因此,尽管经验频率曲线具有方法简单的特点,但在城市暴雨强度公式编制过程中,建议降雨资料应采用理论频率曲线调整,然后进行暴雨强度公式参数拟合。
2 三种理论频率曲线比较
一般采用的理论频率曲线为皮尔逊Ⅲ型分布曲线、耿贝尔分布曲线和指数分布曲线。其中,皮尔逊Ⅲ型分布曲线累积分布函数为[1]:

xp——样本值;

Cv——样本变差系数;
Cs——样本偏差系数。
当Cs=2时,皮尔逊Ⅲ型分布曲线累积分布函数变为[3]:

该式为指数分布曲线的累积分布函数,有解析解。
当Cs=1.1395时,皮尔逊Ⅲ型分布曲线累积分布函数变为[3]:

因此,指数分布曲线和耿贝尔分布曲线实际上是皮尔逊Ⅲ型分布曲线在Cs=2和Cs=1.1395的特例。理论上利用皮尔逊Ⅲ型分布曲线对降雨数据进行调整,能够得到比指数分布和耿贝尔分布更好的结果。但以往多数城市在暴雨强度公式的编制中均采用指数分布曲线,其原因正如邓培德先生所指出的:“皮尔逊Ⅲ型模型是三参数公式,在理论上可以概括耿贝尔分布与指数分布,但现有水文资料实在不够,不可能算得可靠的偏态系数,特别是高偏态与高重现期时不太合适,乙形分布是高偏态的极端形态,就较难适合,此外三参数拟合困难,难以手算与电算,个别城市单独统计实在不容易,且不同拟合方法也有一定差异,计算结果往往因人而异。”[4]
应该承认,在计算机软硬件功能欠发达的年代,求解皮尔逊Ⅲ型分布的最优解存在一定难度。但是,随着时代的进步,皮尔逊Ⅲ型分布最优解的求解方法已经成熟,因此,目前城市暴雨强度公式编制中理论频率曲线应采用皮尔逊Ⅲ型分布曲线,而不仅仅是指数分布曲线。
3 皮尔逊Ⅲ型分布求最优解的三大问题
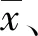
式中:n——样本数;
xi——第i个样本值。


(3)如何判断所求理论频率分布曲线为最优,即拟合准则的选择问题。
4 快速求解皮尔逊Ⅲ型分布曲线
针对皮尔逊Ⅲ型分布曲线累积分布函数(公式(1)),令t=β(x-a0),tp=β(xp-a0),则:
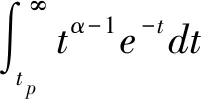
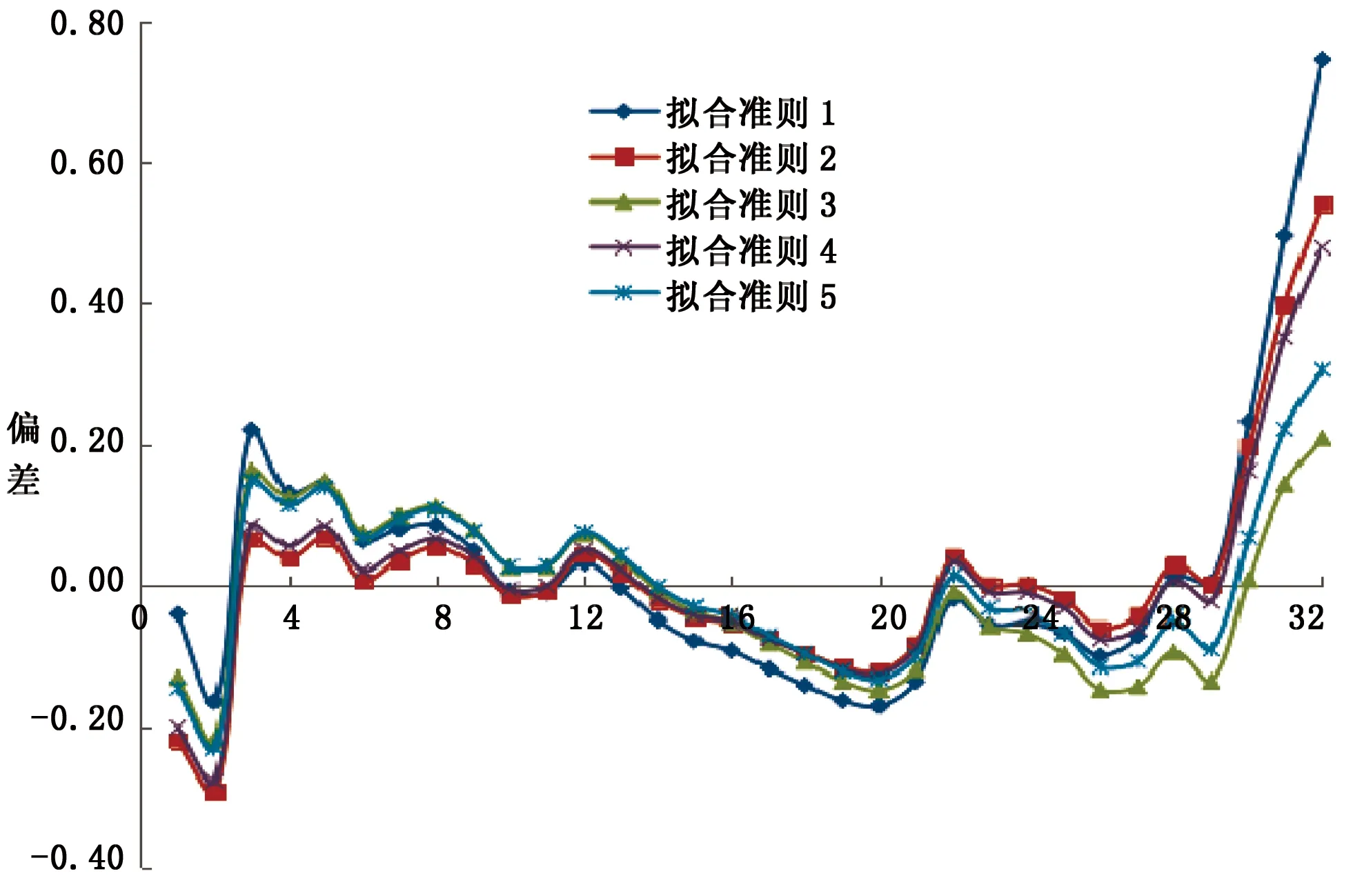
当0 当t≥α+1时,采用连分数形式展开,可以快速收敛,计算公式为[6]: 当t=0时,p(t≥tp) = 0。 该公式收敛速度较慢,使用时用户应根据需要计算出更多的展开项。 当给定频率Ps,可用牛顿迭代法求解对应的t值,迭代公式为[6]: s-1=1,s0=t,q-1=0,q0=1 s-1′=0,s0′=1,q-1′=0,q0′=0 当i(>0)为偶数时: 当i(>0)为奇数时: 因为级数形式和连分式形式的展开式收敛均较快,展开深度i不必太大,建议取10即可。牛顿迭代法中初值t0原则上可取任意大于0的实数,但受斯特林展开式精度的限制,不宜取太大(太大时,迭代计算将会出现数值溢出),建议初值t0取样本t的平均值。迭代次数k由迭代精度ε控制,当给定α,若|tk+1-tk|≤ε|tk+1|,则tk+1为对应于已知设计频率Ps的所求值t。 为判断理论频率分布曲线与原始数据的适合性,常采用的拟合准则有以下5种[8-9]: (1)绝对离差平方和最小 (2)离差绝对值之和最小 (3)相对离差平方和最小 (4)相对离差绝对值之和最小 (5)离差平方相对值和最小 第(1)、(2)种拟合方法,高区数据(高重现期)和低区数据(低重现期)对结果的影响不同(不等权),有可能导致低区数据偏离较大;第(3)、(4)种拟合方法,高区数据和低区数据对结果的影响相同(等权);第(5)种方法则试图在第(1)和第(3)种方法之间寻找平衡。由于目前并不清楚自然界暴雨的准确规律(皮尔逊Ⅲ型分布只能说从统计规律上相对较好),而且原始数据的波动(最大值和最小值之比)又有大有小,所以很难说哪种拟合准则更好。 很多研究者试图通过比较不同理论频率分布曲线拟合误差的大小,衡量理论频率曲线的优劣,这种做法存在以下缺点: (1)指数分布曲线和耿贝尔分布曲线,均为皮尔逊Ⅲ型分布曲线的特例,如果把皮尔逊Ⅲ型分布曲线和它的特例比较,必须有一个前提,即保证皮尔逊Ⅲ型分布曲线为最优形式。而当皮尔逊Ⅲ型分布曲线为最优形式时,其拟合精度必然比它的特例拟合精度高,这是由皮尔逊Ⅲ型分布曲线最优解的求解方法决定的。 (2)撇开皮尔逊Ⅲ型分布曲线,其它4种分布中,即使某种分布的拟合精度更高,也不代表这种分布更优,因为从有限的资料中并不能确定自然界降雨的准确规律。 (3)假如拟合精度高的分布就是更好的分布,那么,不进行任何调整,直接采用经验频率曲线就应该是最好的选择,因为此时拟合误差为0。而前面已经分析过,直接采用经验频率曲线而不采用理论频率分布曲线进行调整是不合理的。 其中,上文的5种拟合准则中的(2)式为目标函数,(3)(4)(5)式为约束条件。 Cvmin= 0.8Cv样本,Cvmax=1.2Cv样本 Cv样本——样本变差系数。 水文学研究表明,暴雨的Cs约为2.5~4.0Cv,采用计算机求解时,可放宽至1.5~5.0Cv。同时,皮尔逊Ⅲ型分布曲线要求样本值x大于等于a0,即: 式中,xmin——样本系列中最小的样本值。 为了确保皮尔逊Ⅲ型分布曲线涵盖指数分布和耿贝尔分布,Cs=2和Cs=1.1395两种情况应包含在内,因此: Csmin=min(1.1395,1.5Cv), 式中:min和max分别表示求最大值和最小值。 皮尔逊Ⅲ型分布曲线最优解的求解最终可表示为: 上式可采用枚举法、遗传算法等方法求解。 应用案例采用枚举法求解皮尔逊Ⅲ型分布曲线最优解,参数取值如下: Cv=(0.8+0.005×j)Cv样本 Cs=min(1.1395,1.5Cv)+ 式中,i,j,k均为整数,且0≤i≤80,0≤j≤80,0≤k≤70,即总共计算465 831种组合情况,这样的精度完全可以满足工程计算的要求。原始数据采用表1降雨资料(5min历时),计算结果如表4所示,拟合结果如图2所示。 表4 皮尔逊Ⅲ型分布曲线调整结果 图2 拟合结果比较图 从表4和图2可以看出: (1)高重现期时,偏差从小到大依次为:拟合准则1、拟合准则3、拟合准则5、拟合准则4、拟合准则2。 (2)低重现期时,偏差从小到大依次为:拟合准则3、拟合准则5、拟合准则4、拟合准则2、拟合准则1。 (3)当重现期为33年一遇时,修正值均比原始值20.3mm小,说明20.3mm的实际降雨重现期大于33年一遇。 (4)当重现期为1年一遇时,修正值均比原始值2.0mm大,说明2.0mm的实际降雨重现期小于1年一遇。 再次重申,在自然界降雨准确规律不确定的情况下,不同拟合准则得到的频率分布曲线不存在优劣之分,使用时应结合其它资料判断。在本文应用案例中,认为拟合准则3选中的可能性更大。 (1)城市暴雨强度公式编制中,降雨资料应采用理论频率分布曲线进行修正。 (2)理论频率曲线应选用皮尔逊Ⅲ型分布曲线,指数分布曲线和耿贝尔分布曲线均为皮尔逊Ⅲ型分布曲线的特例。 (3)只有在理论频率分布曲线和拟合准则均相同的情况下,才能根据拟合精度高低判断频率分布曲线的优劣。

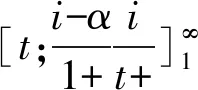
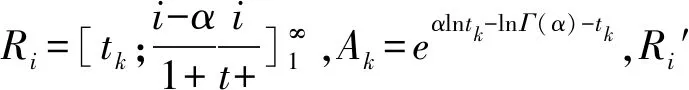
5 拟合准则
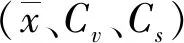
6 皮尔逊Ⅲ型分布曲线最优解

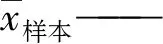
7 应用案例

8 结论
