公共及共享自行车接驳轨道交通方式选择概率

马庚华，孙祎峥，邢金洋，翁心雨，王天童

(1.河海大学 港口海岸与近海工程学院，江苏 南京 210098；2.河海大学 土木与交通学院，江苏 南京 210098)

当前，城市公共及共享自行车系统两者协调发展，服务于居民公共交通出行[1]。基于共享自行车由公共自行车发展而来，两者存在相似性，势必会导致两者间存在一定竞争关系[2]。在公共自行车与共享自行车接驳轨道交通中，竞争结果的体现在于两者接驳概率差异。研究公共及共享自行车接驳轨道交通方式选择对于两者竞争关系的描述具有重要意义。

出行者在计划出行时总是期望选择效用最优的出行模式[3]，而非集计模型的基本思想就是效用最大化[4]，因此公共及共享自行车接驳轨道交通方式选择概率模型以非集计模型作为基础，本文选择二项Logit模型来预测相应方式选择概率，为研究公共及共享自行车接驳轨道交通出行行为奠定基础。

1 二项Logit模型

公共及共享自行车接驳轨道交通过程主要由四部分构成，分别是轨道交通出行、车辆存取、公共及共享自行车出行与步行过程这四部分，因此在非集计模型中的效用函数主要包括这四部分的效用函数。同时，由于公共及共享自行车接驳轨道交通过程中，轨道交通出行部分是重叠的，因此公共及共享自行车接驳轨道交通方式选择模型仅需考虑公共及共享自行车出行、车辆存取与步行过程三部分的效用，如公式(1)所示。

UB&R=Upark+Ubike+Uwalk

(1)

假设有n=1,2,…,N个调查对象，出行者选择方式i接驳轨道交通所获得的效用表示为Uin，Uin为一个随机变量，由固定项Vin和概率项εin构成，如公式(2)所示。

Uin=Vin+εin

(2)

考虑公共及共享自行车接驳轨道交通时，接驳方式分为两类：一类是选择公共自行车接驳轨道交通，即i=1；另一种是选择共享自行车接驳轨道交通，即i=2。因此，出行者选择公共自行车接驳轨道交通的概率如公式(3)所示。

(3)

出行者选择共享自行车接驳轨道交通的概率如公式(4)所示。

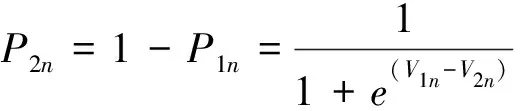
(4)

进一步整理后，如公式(5)所示。

(5)

2 数据分析

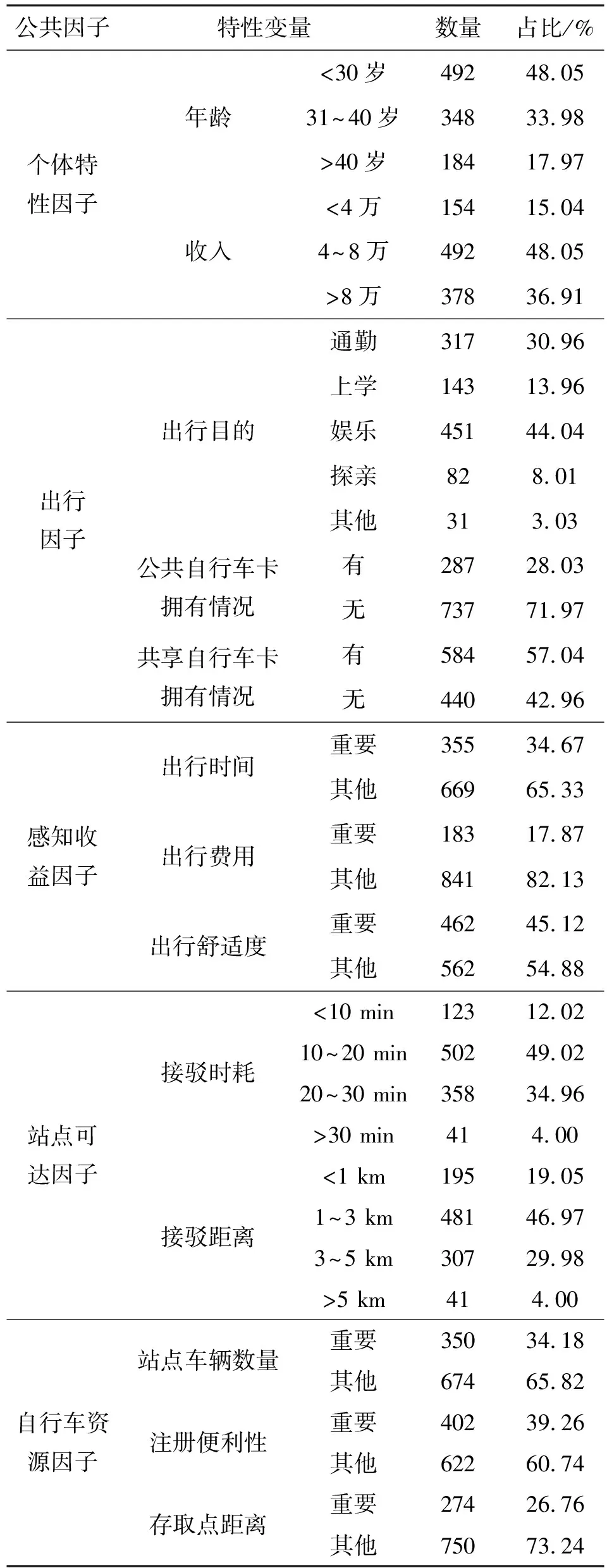
考虑到不同类型轨道站点出行者接驳需求存在一定差异[5]，因此综合多方因素考量，本文采用SP调查法[6]通过在新街口站、珠江路站、草场门站与三山街站进行实地调查。调查问卷主要由三部分构成：出行者的个人信息、出行特征与轨道交通站点特性。第一部分个人信息主要包括性别、年龄、收入等情况，对这部分情况进行调查，有利于获得选择公共及共享自行车接驳轨道交通出行者的群体信息；第二部分出行特征主要包括出行目的、出行过程中的感知因素等，对出行情况进行了解；第三部分主要是相应的轨道站点特性等。通过在四个调查站点进行问卷调查，总计回收1160份问卷，其中有效问卷数量为1024份。最终统计得到相应参数的数量及占比见表1。

3 公共及共享自行车接驳轨道交通方式选择模型建立

3.1 效用函数

公共及共享自行车接驳轨道交通时，两者的效用差决定了该模式的选择概率。根据研究内容采用线性形式来表示效用函数固定项[7]，如公式(6)所示。

(6)

式中：

Xink—出行者n第i个选择方案中的第k个特征变量；

K—特征变量的个数；

θk—第k个变量所对应的参数；

θ′=[θ1,…,θk]—参数向量；

Xin=[Xin1,…,Xink,…,XinK]—出行者n选择方案i的特征向量，表示公共及共享自行车接驳轨道交通方式选择的影响因素。

相应公共及共享自行车接驳轨道交通方式选择的效用函数如公式(7)所示。

(7)

式中：

P1n—出行者选择公共自行车接驳轨道交通的概率；

Xkn—公共及共享自行车接驳轨道交通方式选择模型特征变量。

3.2 参数标定

特征变量Xn是指影响公共及共享自行车接驳轨道交通方式选择的因素[8]。模型标定需要通过实际数据作为支撑，通过对数据进行加工整理，对变量进行离散化处理[9]，从而估计参数θ和选择结果δin。设当出行者n选择公共自行车接驳时，即i=1，选择结果δ1n=1,δ2n=0，因此出行者选择公共自行车接驳轨道交通的概率如公式(8)所示。

(8)

当样本量为N时，选择概率L*如公式(9)所示。

(9)

当L*最大时，得到参数θ的估计值[10]，因此可通过求L=lnL*的最大值得到参数θ的估计值，如公式(10)所示。

(10)

整理后进一步整理后，如公式(11)所示。

(11)

对θ进行求导，如公式(12)所示。

(12)

结合实际情况，整理调查数据得到相应参数及取值见表2。

因此可确定公共及共享自行车接驳轨道交通方式选择概率模型的效用函数如公式(13)所示。

(13)

3.3 参数估计

由于公共及共享自行车接驳轨道交通方式选择概率模型理论基础为二项Logit模型，因此在确定模型特征变量后，利用SPSS软件对数据进行二项Logit回归，预测公共及共享自行车接驳轨道交通方式选择概率[12]。主要利用SPSS软件对模型进行相应参数标定，并通过极大似然检验法剔除不显著的特征变量[13]，最后确定方式选择概率模型的回归参数，得到各站点方式选择模型，预测站点公共及共享自行车接驳轨道交通方式选择概率。下面以新街口站点为例对其数据进行相应分析，整理并保留显著影响因素，得到Logit模型的参数估计与检验结果见表3。将其余三个站点调查问卷数据整理输入SPSS软件中依次进行上述回归分析过程，可以得到各站点调查数据的相应Logit模型参数标定结果见表4。

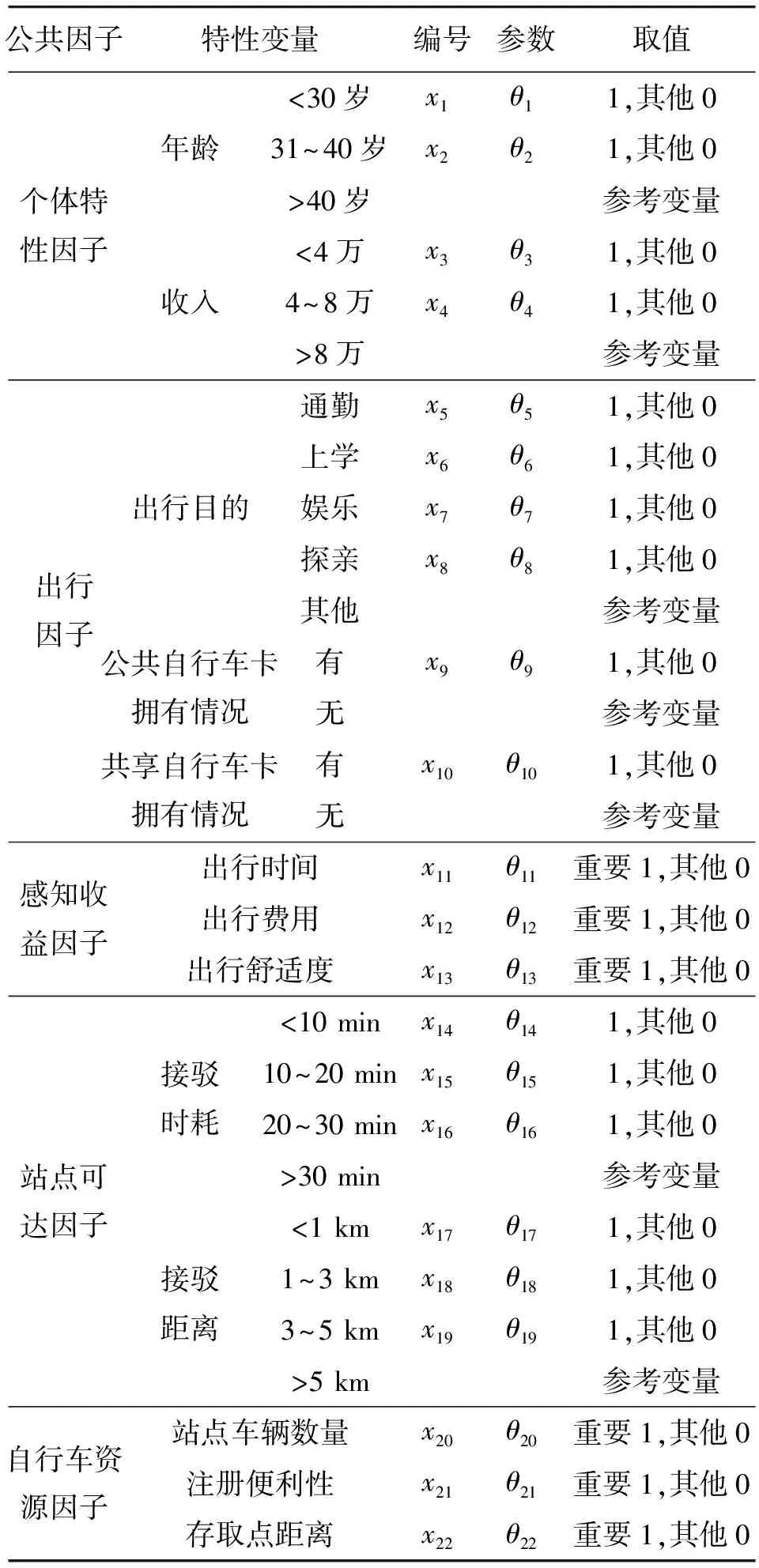
表2 特征变量参数及取值表Tab.2 Characteristic variable parameters and value tables

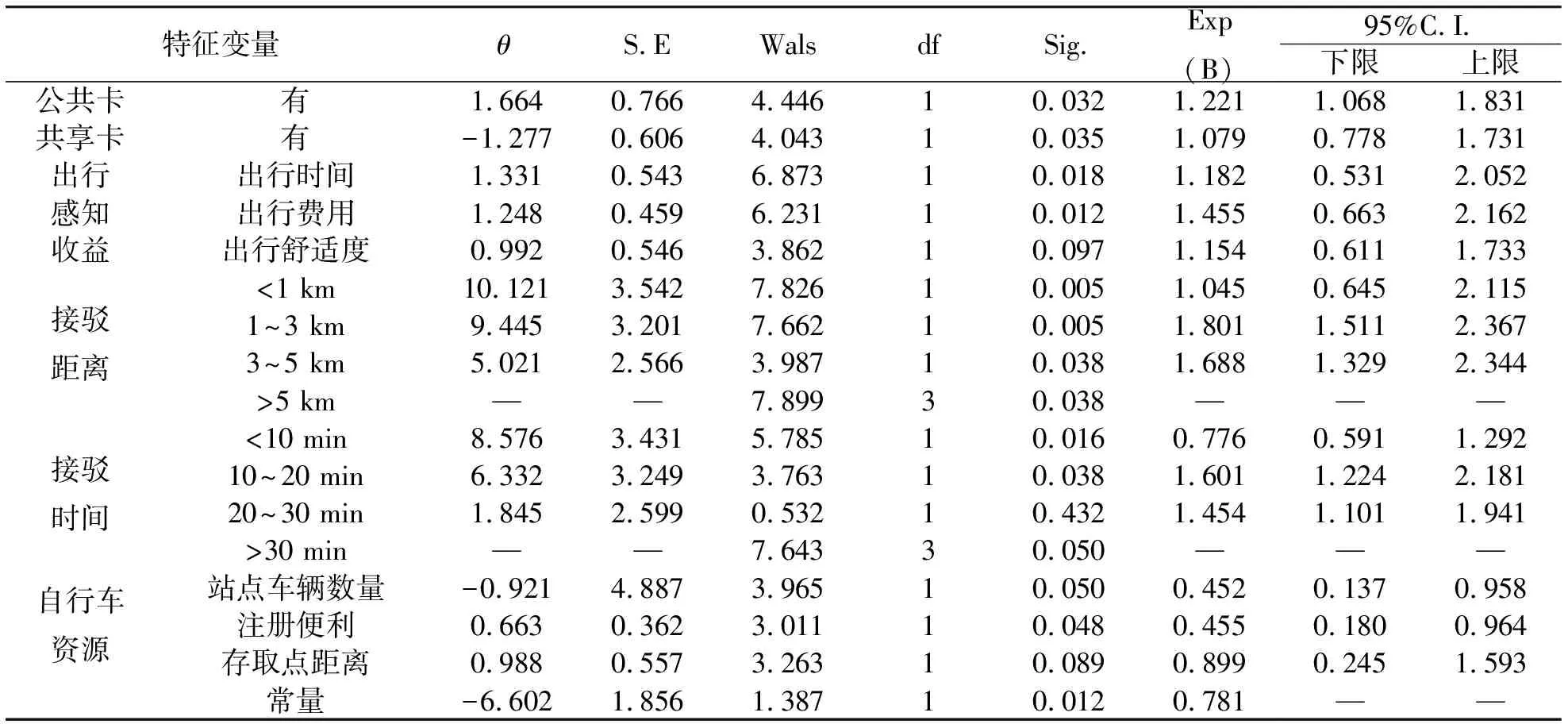
表3 Logit模型参数估计与检验Tabl.3 Estimation and testing of logit model parameters

表4 模型参数标定与检验Tab.4 Model parameter calibration and verification

在确定各站点模型参数的基础上可确定其相应的公共及共享自行车接驳轨道交通方式选择概率模型的效用函数[14]。

新街口站点效用函数计算如公式(14)所示。

(14)

式中：

P11—新街口站点的公共自行车接驳轨道交通概率。

珠江路站点效用函数计算如公式(15)所示。

(15)

式中：

P12—珠江路站点的公共自行车接驳轨道交通概率。

草场门站点效用函数计算如公式(16)所示。

(16)

式中：

P13—草场门站点的公共自行车接驳轨道交通概率。

三山街站点效用函数计算如公式(17)所示。

(17)

式中：

P14—三山街站点的公共自行车接驳轨道交通概率。

4 非集计结果集计化

由于非集计模型研究对象是单个出行者，因此需要采用集计方法将模型计算得出的概率值转化为公共及共享自行车接驳轨道交通方式选择的整体概率值[15]。本文主要按照年龄分类法将被调查者进行分类，确定每一类出行者所占的比例。在分别求出每一类出行者公共自行车接驳概率平均值的基础上，结合相应比例进行加权计算[16]，即可得到相应公共自行车接驳轨道交通方式选择概率值如公式(18)所示。

(18)

共享自行车接驳轨道交通方式选择概率值如公式(19)所示。

P2=1-P1

(19)

式中：

fj—各年龄段被调查者占总体被调查者的人数比例；

P1j—各年龄段出行者选择公共自行车接驳轨道交通概率的平均值；

P1—出行者选择公共自行车接驳轨道交通概率；

P2—出行者选择共享自行车接驳轨道交通概率。

根据各站点数据与公共及共享自行车接驳轨道交通方式选择概率模型，得到单个出行者的公共及共享自行车接驳轨道交通方式选择概率。前文依照年龄将出行者分为<30岁、30～40岁、>40岁这三类，根据已有的个体选择公共自行车接驳轨道交通概率值计算得到这三类出行者的公共自行车选择概率平均值。根据每一类出行者占比，结合这三类出行者选择公共自行车接驳轨道交通概率平均值，可计算得到各站点公共自行车接驳轨道交通预测概率值与共享自行车接驳轨道交通预测概率值，预测结果见表5。

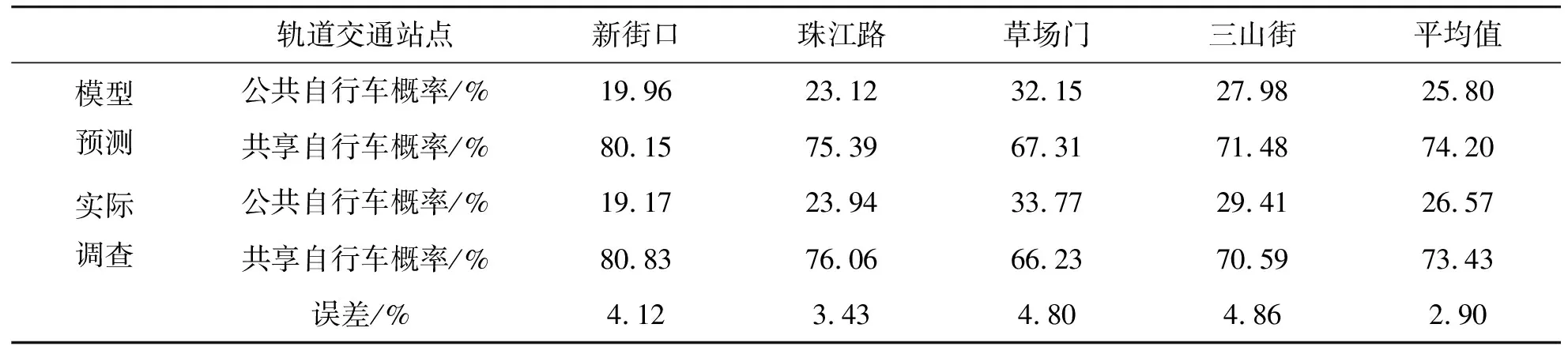
表5 各站点公共及共享自行车方式选择概率表Tab.5 Probability tables for choosing common and shared bicycle modes at each site

5 结论

通过对南京市新街口、珠江路、草场门与三山街四个站点的公共及共享自行车接驳轨道交通方式选择的影响因素进行分析，以二项Logit模型为基础，建立公共及共享自行车接驳轨道交通方式选择模型，将选择结果进行集计化处理，并与实际结果进行比较，发现模型预测值与调查情况整体吻合度较高，符合实际情况。同时，得到各站点公共自行车接驳轨道交通概率值整体低于共享自行车接驳轨道交通概率值，且站点间公共及共享自行车方式选择概率存在明显差异这一结论，与实际接驳选择情况较为符合，说明该模型可以有效预测公共及共享自行车接驳轨道交通方式选择。