熵损失下产品可靠度的E-Bayes估计
2020-01-09许道军费时龙潘保国
许道军,费时龙,潘保国
(1.陆军炮兵防空兵学院 基础部,安徽 合肥 230031;2.宿州学院 数学与统计学院,安徽 宿州 234000)
对于产品可靠度参数的估计,Bayes估计法一直备受人们关注,特别是自从文献[1]提出可靠性参数的多层先验分布之后,多层Bayes估计法在可靠性参数估计中受到很多学者的青睐。但是,正如文献[2]中提到的,用多层Bayes估计法来估计产品的可靠度,一般都要涉及非常复杂的积分计算,很大程度上影响了其在实践中的应用。因此如果各种估计方法的计算结果非常接近时,估计方法的易算性就显得更为重要了。以韩明教授为代表的一批学者开始寻找参数更加简洁的Bayes估计方法。但大多都是在平方损失函数下研究参数的Bayes估计法,而熵损失函数下参数Bayes估计法的研究甚少。
实践中,大多情况下产品寿命的具体分布类型是无法预知的,即使寿命的分布类型是已知的,但获得的实验数据往往仅是失效产品的个数,产品的具体失效时间未知。设某产品的寿命分布类型是未知的,从中随机抽取一个容量为n的样本进行实验,假设在实验时间内有X个样品失效,且各产品是否失效是独立的,则可以认为,一段时间内产品失效个数X是服从二项分布的随机变量
(1)
其中,0 定义1假设随机变量X的概率密度为f(x,θ),其中θ为未知参数。若δ是θ的判决空间的一个估计,则熵损失函数为似然比对数的数学期望,即 设X1,X2,…,Xn是来自二项分布总体的简单随机样本,则根据定义1,其熵损失函数为 容易证明,此损失函数是关于δ的严格凸函数。 引理[5]在熵损失函数下,假设δ是参数θ的判决空间的一个估计,π(θ)是θ的一个先验分布,则参数θ的Bayes估计可唯一地表示为 在(1)式中,取可靠度R的先验分布为其共轭先验分布——Beta分布,其概率密度为 π(R|a,b)=Ra-1(1-R)b-1/B(a,b)。 根据文献[2],选取超参数a与b的时候,应满足π(R|a,b)是关于R的单调递增函数,为此将先验概率密度π(R|a,b)对R求导数得 π(R|a)=aRa-1。 (2) 其中,0 根据文[2],尾部较细的先验分布会造成Bayes估计的稳健性极差,因此应当给超参数a确定一个上限,假设c>1为a的一个上限,这样可以确定超参数a的取值范围为D={a|1 为参数R的E-Bayes估计。 假设对某产品进行m次定时截尾试验,第i次试验样品数为ni,i=1,2,…,m,若第i次试验的结果是容量为ni的样本中有ri(0≤ri≤ni)个样品失效,则将这m次试验的结果记为(ni,ri),i=1,2,…,m。 为了说明超参数a先验分布π(a)的变化对可靠度R的E-Bayes估计的影响,下面将在超参数a的3种不同的先验分布下,分别计算可靠度R的E-Bayes估计,并进行比较。 1) 在熵损失函数下,可靠度R的Bayes估计为 2)若超参数a在D上的先验概率密度π(a)分别由(3)~(5)式表示: (3) (4) (5) 则对应的可靠度R的E-Bayes估计分别为 1)]; (6) (7) (8) 证明1)根据文献[3],参数R的似然函数为 若参数R的先验概率密度π(R|a)由(2)式表示,则R的后验概率密度为 h(R|N)∝π(R|a)L(R|r)=aRN+a-r-1(1-R)r。 即R|N~Be(N+a-r,r+1),故在熵损失函数下可靠度R的Bayes估计为 若(2)式的超参数a在D上的先验概率密度π(a)由(3)式表示,则根据定义2,可靠度R的E-Bayes估计为 定理2若超参数a在D上的先验概率密度π(a)分别由(3)~(5)式表示,则当c>1时,有 f′(x)>f′(0)=0,所以f(x)>f(0)=0,故当 为了便于将可靠度R的E-Bayes估计与其对应的多层Bayes估计进行比较,以下分别在(3)~(5)式下计算出可靠度R的多层Bayes估计。 若可靠度R的先验概率密度π(R|a)由(2)式表示,超参数a的先验概率密度π(a)分别由(3)~(5)式表示,则根据文献[1]的方法,可得参数R的多层先验概率密度可分别表示为(9)~(11)式: 0 (9) (10) (11) 定理3对失效个数服从二项分布的产品进行m次试验,实验结果为(ni,ri),i=1,2,…,m,若参数R的多层先验概率密度π(R)分别由(9)~(11)式表示,则在熵损失函数下可靠度R的多层Bayes估计可分别表示为(12)~(14)式: (12) (13) (14) 证明若参数R的多层先验概率密度π(R)由(9)式表示,根据Bayes定理知,R的多层后验概率密度为 在熵损失函数下,可靠度R的多层Bayes估计为 同理,若参数R的多层先验概率密度π(R)分别由(10)式和(11)式表示,则可靠度R的多层Bayes估计可分别表示为(13)式和(14)式。 文献[5]给出了某型电子元件在定时截尾试验中获得的实验数据(假设产品失效时间不详),具体数据见表1。 表1 某电子元件失效数的定时截尾实验数据Tab.1 The failure data of an electronic component under censoring life test 表2 某电子元件可靠度R的E-Bayes估计和多层Bayes估计Tab.2 The expected and hierarchical bayesian estimation for reliability of an electronic component

1 可靠度R的E-Bayes估计
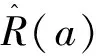

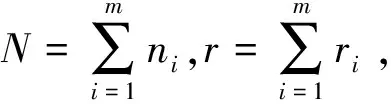







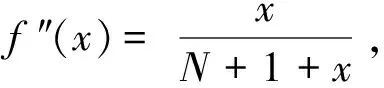



2 可靠度R的多层Bayes估计


3 数值比较



