基于SIMULINK的退役动力锂电池建模与仿真
2020-01-09陈杨明
陈杨明
(1.重庆大学电气工程学院,重庆 400044;2.云南电网有限责任公司研究生工作站,昆明 650217)
0 前言
动力锂电池以其相对优越的性能成为新能源汽车储能系统的首选。然而,车用动力锂电池的寿命只有短短几年,锂离子电池从新能源汽车上退役后仍有高达80%的剩余容量,有较高的利用价值,可依据其电池性能继续应用在小型动力系统和电网储能等场合。为了实现退役动力锂电池分级梯次利用的目标,就必须确保电池管理系统(Battery Management System,BMS)能有效管理退役锂电池在各等级剩余电量(State of Charge, SOC)下的充放电状态。为了设计有效的BMS,首先应结合锂电池模型和相关应用工况进行仿真分析。
现有电池模型主要可分为三类:实验参数模型、电化学模型和等效电路模型。实验参数模型无法保证锂电池在动态工况下SOC 估计的准确性。电化学模型过于复杂,在仅需考虑电池充放电性能的场合不便使用。等效电路模型基于电池工作原理用电路网络来描述电池的工作特性,适用于多种电池,特别是从电池使用和管理等角度分析问题的时候。
综上,在车用锂电池应用分析中应该可以等效电路模型,在考虑循环寿命对电池性能影响的基础上,该模型也同样适用于退役锂电池的梯次利用过程。基于此,本文在给出锂电池模型的基础上,选取建模软件Simulink,利用简易可行的参数辨识方法,搭建了退役锂动力电池的仿真模型,并验证了模型的有效性。
1 动力锂电池模型的建立
1.1 常规锂电池模型
锂动力电池的典型放电特性曲线如图1 所示。

图1 锂动力电池的典型放电特性曲线
锂电池典型放电曲线可以分成三段:第一阶段为指数放电区域,此阶段电池开路电压(Open Circuit Voltage, OCV)从满电状态时的满电压开始的很快下降到标称的电压值;第二阶段是标称放电区域,此阶段OCV 能在大容量放电区域内保持稳定,不会跌落太多;第三个阶段是深度放电区域,此阶段的放电容量接近最大的容量,OCV 迅速跌落。
锂电池放电过程的数学模型基本框架与Shepherd 电池模型类似,即把OCV 当做SOC的函数形式,同时考虑极化内阻对OCV 的影响,则有电池电压的推导公式为:

其中参数定义为:
Vbatt为电池端电压(V)
E0为电池的电压常量(V)
K为极化常数,单位为V/Ah
Q为电池容量(Ah)
it=∫idt,为电池真实点电荷数(Ah)
B为指数区域的时间常数,单位为(Ah)-1
R为电池内阻(Ω)
RP为电池内阻(Ω)
i为电池电流(A)
i*为滤波后电流(A)
公式中的RP·it代表极化电压,用于反映电池的OCV 特性;RP称为极化电阻,用于反映电池充、放电接近完成的阶段的特性;i*是对电池电流i一阶低通滤波得到的。
相对于锂电池的放电过程,锂电池的充电电压数学模型区别仅在于极化电阻的区别;这是由锂电池充、放电的特性不同导致的,设充电时的极化电阻RPc为:

最终得到锂电池充、放电时的数学模型为:

1.2 锂电池参数确定
通常,在锂电池出厂时,电池厂家给出的数据手册中都会提供如图1 所示的电池放电特性曲线图,从图中能读出指数放电区域结束点的放电量Qexp、端电压Vexp和标称放电区域结束点的放电量Qnom、端电压Vnom,以及电池的最大容量值Q和Vfull,剩下的就是求解出未知的E0、A和B等参数。
为了能确定E0、A和B等参数的值,需要利用已知的特定工作点来求解方程组。在充满电之后,充电的电量为0,低通滤波得到的i*为0,从而得到:

在指数放电区域结束点,参数B 可以近似认为是3/Qexp;稳态时,可以得到电流i*与i是相等的,就可以得到公式:

同样在标称放电区域可以得到公式:

联立方程-,就能解出E0、A和B等参数,最终得到电池的充、放电模型。
1.3 考虑循环寿命的影响
锂电池出厂后,在电动汽车中使用一定循环次数后退役,电池容量下降到80%左右。结合电池使用过程数据记录和循环寿命对电池性能影响的模型,便可获得电池在退役时的性能状态值。
对于锂电池来说,循环寿命对电池容量和内阻的影响可用下列方程表示:

其中各参数定义为:
Th是半个循环周期,单位秒(s)。整个循环周期为电池完成一次完整的放电再充电(或充电再放电)的时间。
QBOL是电池投入使用之时(Beginning of Life, BOL)的容量,单位安时(Ah)。
QEOL是电池结束使用之时(End of Life,EOL)的容量,单位安时(Ah)。
RBOL是电池投入使用之时的内阻,单位欧姆(Ω)。
REOL是电池结束使用之时的内阻,单位欧姆(Ω)。
ε是电池寿命因子。在电池投入使用时和结束使用时,该寿命因子的取值分别为0 和1。
电池寿命因子ε可用下列方程表示:
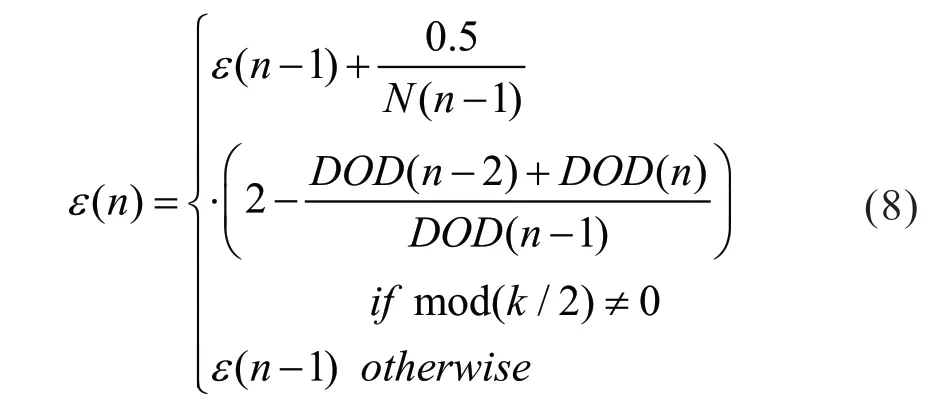
其中:
DOD(Depth of Discharge)也称放电深度,是电池在半个循环周期(放电过程)内放出电量与电池总容量的比值,用百分数表示。
N 表示最大循环次数,它与电池设计寿命、放电深度、工作温度、放电电流和充电电流有关,可以利用下列公式迭代来进行估算:

其中:
H 表示循环次数(常数),相当于1C 放电情况下的设计寿命。
ζ表示放电深度的指数因子,通过电池实验获得“放电深度-循环寿命”曲线拟合求解。
Ψ表示循环次数的Arrhenius 因子。
Idis_ave是半个循环周期的平均放电电流。
Ich_ave是半个循环周期的平均充电电流。
γ1是考虑放电电流影响的指数因子,通过电池实验获得“不同倍率放电电流-循环寿命”曲线拟合求解。
γ2是考虑充电电流影响的指数因子,通过电池实验获得“不同倍率充电电流-循环寿命”曲线拟合求解。
综述所示,结合基本的锂电池充放电模型,再考虑循环寿命对锂电池性能的影响,即可模拟退役锂电池继续工作时的充放电特性,从而为退役锂电池梯次利用过程中的电池管理系统的仿真开发等应用提供电池模型。
2 仿真及验证
在分析和建立锂电池的数学模型之后,就可以利用Simulink 软件搭建相应的锂电池模型,并根据仿真结果验证电池模型的可行性。
2.1 模型搭建

图2 锂电池充放电模型
根据公式和可以得到锂电池数学模型的框图如图2 所示。用集中电阻模拟电池的内阻,它随着锂电池充放电循环次数的增长而发生相应的改变。对电池输出电流积分就可以得到放电电荷量it;电池输出电流经一阶低通滤波器滤波之后就能得到电流i*;通过判断输出端电流的方向,选择启用充电模型或者放电模型,就能得到电池开路的端电压Ebatt。
根据图2 所示结构框图,在Simulink 中搭建锂电池仿真模型,仿真验证选取A123 公司的ANR26650 型号锂电池产品。从该电池数据表中提取模型所需参数如表 1 所示。

表1 锂电池模型特征参数
2.2 锂电池模型仿真验证
利用搭建好的锂电池模型,仿真不同功率放电时电池的OCV 的变化,Simulink 的恒功率放电模型如图3 所示。

图3 Simulink仿真模型
由于电压与电流的乘积就是功率,故通过检测电池的端电压来确定受控电流源的电流大小,达到恒功率输出的要求。同时为了避免代数环的错误,在电流指令上加入了memory 模块,并在电池电量小于1%时停止放电。最终得到不同功率放电工况下的恒功率放电曲线,与电池厂商提供的电池出厂说明书上的恒功率放电曲线对比图如图 4 所示。

图4 锂电池恒功率放电过程仿真与实验波形对比图
在图4 中,虚线为Simulink 仿真得出的“电压-容量”曲线,实线为厂商提供的实测的放电曲线;可以看出,不管什么等级的恒功率放电过程,在绝大多数区域,仿真得出的放电曲线与实测放电曲线都非常接近,完全能满足工程应用的需求。
当然,在Simulink 中搭建的电池模型也存在一定的缺陷和不足。引起模型仿真结果产生偏差的原因包括:(1)仿真模型认为内阻不变,在实际条件中,内阻会随着电池不同工况而变;(2)仿真没有考虑不同工作温度对电池性能的影响;(3)仿真模型没有考虑电池任何寄生参数对性能的影响。虽然建立的模型存在一定的缺陷,但是仿真验证了模型的正确性,可以作为模拟电池性能的一个参考。
3 结束语
本文通过对典型电池放电曲线的分析,构造了电池的放电曲线的拟合公式,建立了锂电池充放电过程的数学模型;通过引入锂电池循环寿命对电池性能的影响,得出退役锂电池的仿真模型。然后利用Simulink 的图形化的编程搭建了锂电池的仿真模型,最后通过仿真结果与实际电池放电波形对比,验证了电池模型的正确性。通过引入循环寿命对电池性能的影响,进一步仿真验证了退役锂电池模型的可行性,为接下来的退役锂电池梯次利用的开发提供可靠的电池模型。
