基于加权最小二乘分布式电源电力系统状态估计

郑锐邦

（云南电网有限责任公司西双版纳供电局，云南 西双版纳 666100）

0 前言

分布式电源（Distributed Generation，DG）是指输出功率为数千瓦到50 MW 的小容量发电装置，不仅可以独立供电，而且可以接入输电网，与大电网一起为用户统一供电[1]。其主要安装在用户附近，是一种新型能源系统，与电力系统结合形成了新型电力系统，该系统具有极强的高效性和灵活性。新型电力系统的出现不仅提高了供电的电能质量，而且可以提高供电可靠性和稳定性[2]。

但是随着DG 并网比例逐渐提高，DG 发展面临的问题也逐步凸显，DG 并网给电网带来了许多急需解决的新问题，如对电网电压水平、系统暂态稳定性、电能质量等带来影响，加大了系统安全稳定运行的难度。为了保证系统安全、稳定和经济的运行，有必要对分布式接入电网后的状态估计问题进行研究，以便于对电网更好的进行监控，提高电能质量，满足未来智能电网的需要。

本文通过研究含分布式电源的加权最小二乘法电力系统状态估计，分析分布式电源并网对电网的影响，以便对电网进行更好的监控，保障电力系统安全、稳定和经济运行。

1 含分布式电源的电力系统状态估计

电力系统状态估计可以认为是某种意义上的实时潮流计算，它根据节点注入有功和无功功率、支路有功和无功潮流或电流、节点电压等状态模拟量的量测结果估计出符合电路定律系统的实时潮流分布[3]。

加权最小二乘状态估计是最早发展起来的状态估计，加权最小二乘估计法是电力系统静态估计最经典的方法，也是最常用的方法之一。该方法以残差即量测量z和量测估计量之差的平方和最小为目标准则。

对给定系统具体网络结构、支路参数和状态变量后，量测矢量z可以表示为：

式中：z—量测向量[4]（通常包括系统节点注入有功和无功功率、支路有功和无功潮流以及节点电压幅值等）；

h(x)—非线性量测函数；

v—量测误差。

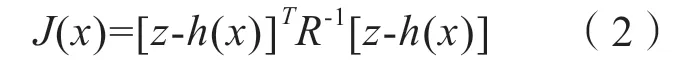
达到最小值的x值。

2 含分布式电源状态估计的实现方法

根据加权最小二乘状态估计的数学模型，可以得到含分布式电源状态估计的量测的修正方程和迭代方程[5]：

根据迭代方程式（4）进行修正，直到目标函数J(x)接近于最小值，收敛判据为式（5）：

式中：εx—按精度要求选取的收敛标准。εx一般取基准电压幅值的10-4～10-6。

本文中分布式电源（Distributed Generation,DG）统一假定为PQ 恒定的模型[6]，DG 的接入为以恒定有功功率和无功功率注入系统节点，即在系统中接入DG 相当于系统中增加一个发电机。

分布式电源的接入改变了系统的网络拓扑结构，因此需要重新进行潮流计算以获取状态变量的真值和完成状态估计所需的量测值[7]。本文选取选取牛顿拉夫逊法来处理对个DG 接入电力系统的潮流分布计算获取状态估计所需的量测值。

分布式电源（DG）接入节点系统后，通过牛顿拉夫逊对节点系统进行潮流计算[8]，求解出含分布式电源状态估计的真值，节点系统的电压的幅值和相角；含分布式电源状态估计的量测量，系统相应节点注入有功功率和无功功率、支路有功潮流和无功潮流，然后使用量测量结合加权最小二乘数学模型进行状态估计，最终求出状态估计的值，并与潮流计算出的真值进行对比分析，以绝对误差和相对误差来衡量状态估计的准确性。其中含分布式电源状态估计的流程图如1 所示。

图1 含分布式电源加权最小二乘状态估计流程图

3 仿真分析

本文选取IEEE14 和IEEE30 节点系统为研究对象，在Matlab 2014a 仿真平台上对研究对象进行状态估计，并以绝对误差和相对误差作为评价指标评价状态估计的精度。计算过程的数据均以标幺值表示，其基准值为100 MVA，电压幅值也为标幺值，相角单位为度。通过使用牛顿拉夫逊法进行潮流计算出电压的幅值和相角作为状态变量的真值，对比分析状态估计算出的状态变量和真值，评价状态估计算法的有效性和合理性。程序中引用数据文件为case14 和case_ieee30。

对于接入的DG 的PQ 注入不等式约束为[6]：

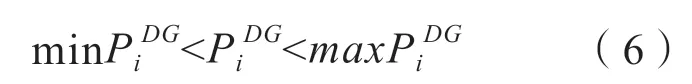
3.1 IEEE14系统仿真分析

本文分别在IEEE14 节点系统供电负荷区的关键节点4，9，14 接入合适容量的DG，以单个节点接入、两个节点同时接入和三个节点同时接入，并使用含分布式电源的状态估计算法进行状态估计。

根据状态估计结果的相对误差，分别取其绝对值求解状态估计的估计偏差平均值。求解出仿真实验中状态估计的平均偏差（见表1）。

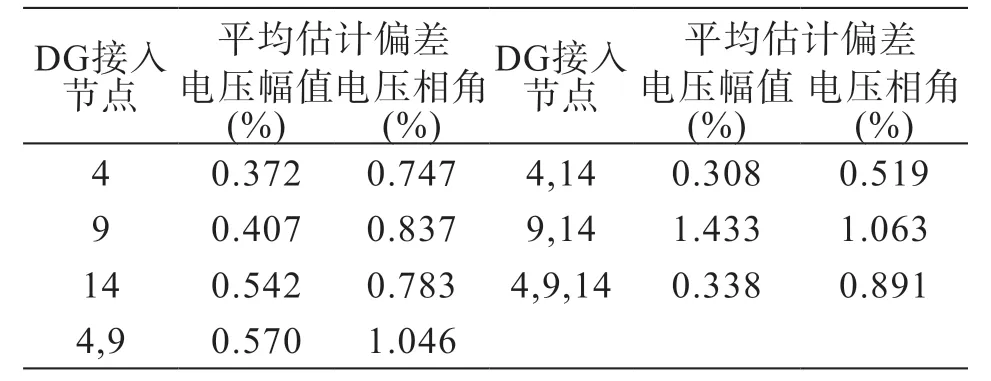
表1 DG接入IEEE14系统平均估计偏差

由表1 中的数据可以看出，电压幅值最大平均估计偏差为1.433%，电压相角最大平均估计偏差为1.063%。状态估计的误差均小于5%，估计精度达到95%以上。实验结果表明：状态估计误差较小，状态估计精度高。因此，可认为本章提出的含分布式电源的状态估计算法合理有效。

3.2 IEEE30系统仿真分析

根据DG 接入的不等式约束在关键节点分别对IEEE30 节点系统供电负荷区的关键节点7，17，21，30 接入适当容量的DG，并对不同情况的DG 接入进行状态估计，然后分析状态估计结果。

根据IEEE30 节点系统关键节点分别接入单个DG 的状态估计的状态变量、绝对误差和相对误差，可以求解出单个DG 接入IEEE30 节点系统的平均估计偏差见表2 所示：

表2 单个DG接入IEEE30系统平均估计偏差

对多个DG 接入IEEE30 节点系统，例如在节点7 和17 同时接入DG、在节点7，17，21同时接入DG 和节点7，17，21，30 同时接入DG 等，并对这些不同情况的DG 接入进行状态估计，并与状态变量真值对比求解绝对误差和相对误差。本仿真实验通过单个DG 和多个DG接入IEEE30 节点系统，运用含分布式电源加权最小二乘电力系统状态估计算法对其进行状态估计，对求解出的状态变量与状态变量的真值（潮流计算出的电压幅值和相角）对比，求出状态估计的绝对误差和理论误差，求解出状态估计的平均估计偏差，由表2 和表3 可以看出电压幅值的最大估计偏差为0.827%，相角最大估计偏差为1.189%，均小于5%，并且在仿真实验过程中发现DG 注入的有功主要影响电压相角，无功功率主要影响电压幅值。

3.3 分布式电源并网对电压分布影响分析

3.3.1 DG接入位置对状态估计电压的影响

分布式电源并网前，运用加权最小二乘状态估计法对IEEE14、30 节点系统进行状态估计， 然后选取容量相等的分布式电源以不同方式接入IEEE14、30 节点系统进行试验，分别进行状态估计，提取估计结果中的电压幅值，并绘制IEEE14 节点系统状态估计的电压分布曲线图（如图2 所示）、IEEE30 节点系统电压分布曲线（如图3 所示）。

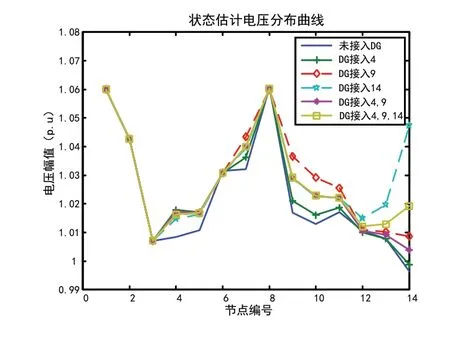
图2 IEEE14系统不同位置接入同容量分布式电源的电压分布

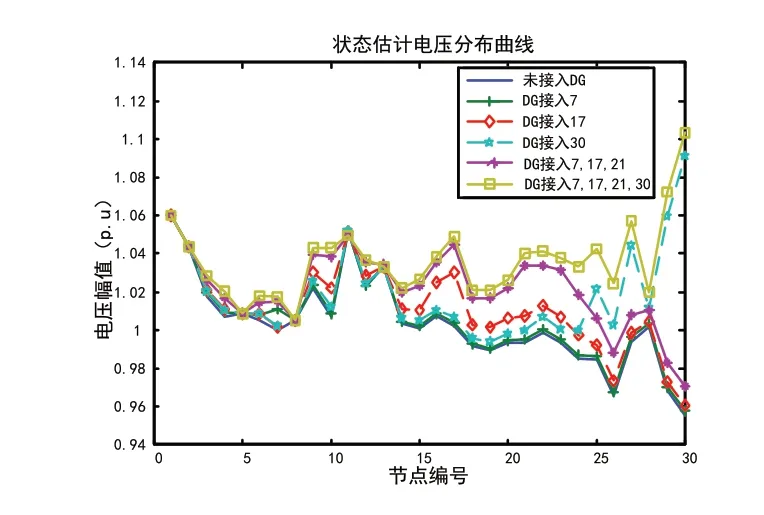
图3 IEEE30系统不同位置接入同容量分布式电源的电压分布

根据图中曲线可以看出当分布式电源接入节点系统后，状态估计出的节点电压增大，电压水平明显提升。总容量相同的分布式电源，接入节点系统在不同的位置或不同位置组合，得到的状态估计电压分布便存在差异。容量相同的DG 接入不同节点，对电压分布影响不同，当DG 接入末端节点时，对电压的分布影响较大，而且总容量相同DG 平均接入多个节点比单独接入一个节点对电压水平的提升更为明显。根据图中曲线还可以看出DG 接入节点后，系统自带发电机的节点电压水平基本不变。

DG 对状态估计电压分布的影响可概述为：

1）分布式电源越接近节点系统中的发电机，对状态估计电压分布的影响越小。

2）分布式电源接入节点系统的多个节点上对状态估计电压幅值的增大效果要好于集中接入同一节点。

3）分布式电源不适合接入节点系统的末端，若接入节点系统末端会增大电压的变化率，影响系统稳定性。因此，分布式电源一般接入系统大负荷节点或者节点位置组合接入。

3.3.2 分布式电源并网容量对状态估计电压的影响

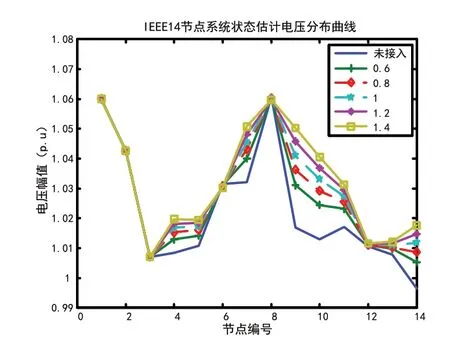
图4 IEEE14系统在9节点接入不同容量的DG时的电压分布

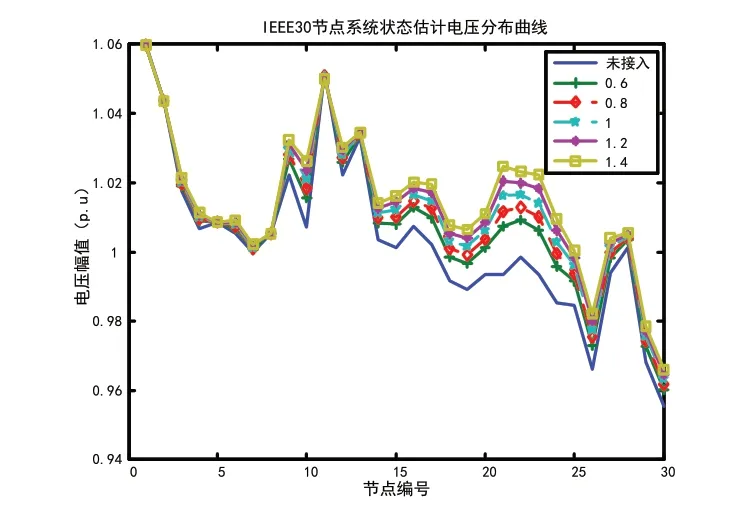
图5 IEEE30系统在21节点接入不同容量的DG时的电压分布

选择IEEE14 节点系统节点9 和IEEE30 节点系统节点21 进行试验，分别按照DG 容量为该节点负荷的0.6，0.8，1，1.2，1.4 比例接入分布式电源，进行状态估计，得出各节点电压，将其整理绘图，如图4 和图5 所示。

根据电压曲线可以看出分布式电源容量越大对状态估计结果中末端节点的电压水平提升越明显，按比例为1.4 接入DG，IEEE14、30节点系统的末端节点的电压水平提升能力最强，但是此时节点电压可能非常逼近安全电压的上限了，这样一来对电力系统安全造成了隐患，如果接入节点负荷大量切除，电压瞬间将会超过安全电压，因此按照负荷比例的0.8 和1 接入对电压支撑能够达到较好的效果。仿真结果表明不改变DG 接入节点系统位置的情况下，DG的总容量决定状态估计的电压提升效果。DG 总容量越大，与节点负荷的比值越高，状态估计电压提升效果就越好，整体电压水平就越高。

3.4 分布式电源并网对网损影响

3.4.1 分布式电源容量对网损的影响

1）单分布式电源

分别在IEEE14，30 节点系统的负荷集中区域的关键节点接入DG，进行状态估计计算出系统的网络损耗。

对IEEE14 节点系统关键负荷区4,9,14 关键节点按与本节点负荷成比例0.6，0.8，1，1.2，1.4 接入DG，进行状态估计，计算出系统网损。

对IEEE30 节点系统供电负荷区7,17,21,30关键节点按照其容量与本节点负荷成比例0.6，0.8，1，1.2，1.4 接入DG，进行状态估计，计算出网损。

两个系统网损变化趋势相同，因此选取IEEE14 节点系统网损变化数据分析DG 接入容量对系统网损的影响，绘制不同容量DG 接入IEEE14 系统不同节点的有功、无功网损变化趋势图（如图6a 和图6b），由坐标图观察分析DG 接入网损的变化规律。

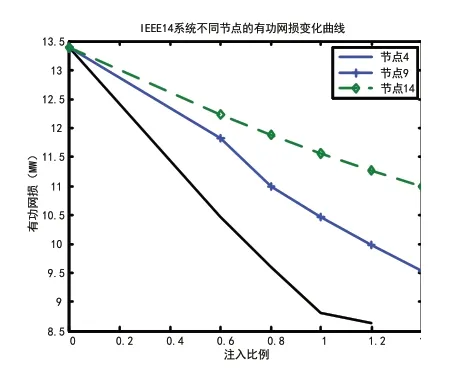
图6a 不同节点的有功网损变化趋势

图6b 不同节点的无功网损变化趋势

由图6a 和图6b 可以看出，无论是有功损耗还是无功损耗都有一个规律性的变化趋势，即当DG 接入后系统的网损逐渐降低。对比分析接入不同节点时有功损耗和无功损耗的变化，接入节点4 的网损下降最快，原因是节点4 为大负荷节点，DG 接入容量较大。因此，可分析得到随着接入DG 容量的增大，有功和无功网损将逐渐减小，并且可以预测网损将减小到一定值后又将逐渐增大。原因为由于分布式电源越接近负荷节点，所以其供给的电能越多，需要从其他节点传输的电能就越少，系统中传输的电能越少，则网络损耗固然减少，这样就大大的节省了网络上损耗的电能，这更说明了分布式电源的优越性。

2）多个分布式电源同时接入

因为单个分布式电源输出的有功有限，为了验证系统网损将随着接入DG 容量的增大而呈现先减小后增大的趋势，因此，选取IEEE14、30 节点系统同时接入多个DG，每个负荷节点先后以DG 最大容量50 MW 接入，进行状态估计得到每次接入的网损，对结果进行分析处理，绘制坐标曲线（如图7 和图8）。

图7a 多个DG同时接入IEEE14系统有功网损变化

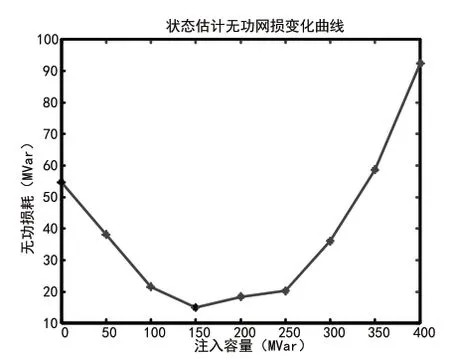
图7b 多个DG同时接入IEEE14系统无功网损变化

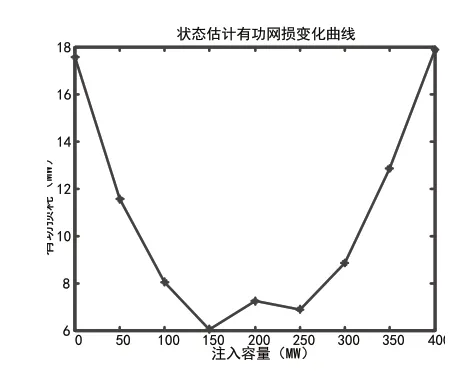
图8a 多个DG同时接入IEEE30系统有功网损变化

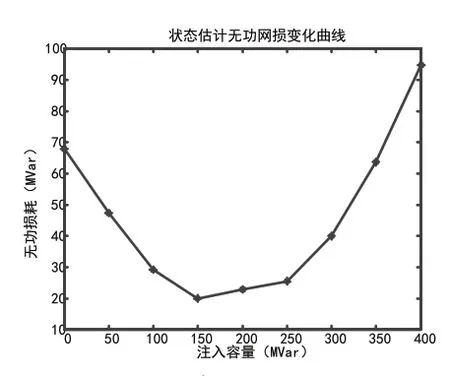
图8b 多个DG同时接入IEEE30系统无功网损变化

根据单个分布式电源接入不同节点和多个分布式电源接入IEEE14、30 节点系统状态估计结果中的网损变化，可以得到结论：系统网损随着DG 注入的容量的增大而逐渐减小，当减小到一定值时，然后随着DG 注入容量的增大而增大。原因为DG 的并

网能够提高系统电压水平，减小网损，然而随着DG 并网容量的增大且当达到一定值时，潮流会逆向运行，导致网损增大。

3.4.2 分布式电源容量接入位置对网损的影响

从另一个角度来分析分布式电源对网络损耗的影响，研究相同容量DG 接入系统其位置对系统网络损耗的影响。

表3 相同容量的分布式电源接入IEEE14各节点时的总网络损耗

表4 相同容量的分布式电源接入IEEE30各节点时的总网络损耗

由表中可以观察出，对于IEEE14 系统节点4 为大负荷节点，节点7 为IEEE30 系统中的大负荷节点，而这两个节点处的有功网损最小，无功网损也最小。因此，可以得到结论：分布式电源接在大负荷节点可以大大减少系统内部支路上流过的电流，大大的减少了网络损耗，即就近供电的原则。

4 结束语

本文在加权最小二乘的理论基础上，应用加权最小二乘状态估计法对注入分布式电源的IEEE14，30 节点系统进行状态估计，对比分析并网前后的结果，研究分布式电源并网对状态估计的影响，得到的结论具体如下：一是分布式电源并网能够增强状态估计结果的电压水平，而且对状态估计电压分布的影响与接入的位置有关。DG 越接近节点系统中的发电机，对状态估计节点电压分布的影响越小；DG 接入节点系统的多个节点时对状态估计电压幅值的增大效果要好于集中接入同一节点；DG 适合采用接入系统大负荷节点或者节点位置组合接入。二是不改变DG 接入系统节点位置的情况下，状态估计电压提升效果由DG 的总容量决定，并且DG 接入系统中部大负荷节点，容量与节点负荷接近时对状态估计电压水平的提升效果最好。三是分布式电源并网能够减小系统网损，DG 接入大负荷节点就近供电时系统网损减小值最大，另外随着DG 接入容量的不断增大，系统网损先减小后增大。

本文在分布式电源并网对状态估计的影响方面进行了一些积极的探索和研究，并取得了一些研究成果。结合本文的研究工作，对下一阶段值得研究的问题作如下展望：一是可以研究对加入的分布式电源PQ 注入的等式约束问题。二是可以进一步优化分布式电源的配置问题，选取多个优化目标，建立优化模型，并考虑分布式电源的后备性，寻找多目标最优的分布式电源配置。