一种低频振荡主要振荡模式识别方法

司大军

（云南电网有限责任公司电网规划建设研究中心，昆明 650011）

0 前言

电力系统稳定性一般可分为功角稳定、电压稳定和频率稳定三类[1-2]。其中电力系统功角稳定还可以进一步分为以下三类：静态稳定、暂态稳定和动态稳定。对于电力系统动态稳定性的判断，需要计算相关信号（如：发电机功角、线路有功、节点电压、节点频率）的阻尼比，阻尼比小于某一阈值，则认为电力系统动态失稳，反之则认为动态稳定。对于N 台发电机组成的电力系统，将有N-1 个振荡模式。在干扰（如故障）情况下，这些振荡模式将在电力系统功率、电压、频率、功角等相关信号中有所体现。对于电力系统动态稳定分析来说，需要在所关心的信号中找出最弱的几个振荡模式，根据其阻尼比，判断电力系统的稳定性（如：阻尼比小于3%认为阻尼不足，系统动态失稳）。

目前主要使用Prony 分析计算所关注信号的振荡模式[3-4]，计算出的振荡模式往往有几十个。若直接在Prony 分析结果中找出几个阻尼比最小的振荡模式进行动态稳定性的判断，则很容易出现误判。这是因为，Prony 分析本质上是病态矩阵的求解，其解易受信号噪声的干扰[5]，使得幅值很小的振荡模式的出现较大的误差；若选择了小幅值振荡模式的阻尼比进行运行稳定性的判断，则误判可能性很高。实际中，一般找出前若干个幅值较大的、振荡频率在低频振荡范围内的振荡模式作为主要振荡模式，并根据主要振荡模式的阻尼比判断系统是否动态稳定。但是，当主要振荡模式较多时容易“遗漏”幅值较小、阻尼比低的振荡，造成动态稳定的误判。另外，选择多少个幅值较大的振荡模式进行判断也因人而易，没有客观的选择标准。为克服人工判断主要振荡模式的不足，本文提出一种电力系统低频振荡主要振荡模式识别方法，从Prony 分析结果中找出主要振荡模式。

1 识别思路

Prony 分析是计算阻尼比的重要手段，通过Prony 分析可以将离散时域曲线X(n) 分解为M个形式为Aie-αitcos(wit+θi)的振荡模式，即：

其中，n={1,2,3,…… ,N}，XM(n) 为由Prony结果拟合得到的曲线，Ai为第i个振荡模式的幅值，αi为第i个振荡模式的衰减时间常数，wi为第i个振荡模式的角频率，θi为第i个振荡模式的衰减时间相角，Ts为X(n)的采样间隔。各振荡模式阻尼比Di为：

本文以下分析均假定Prony 分析结果各振荡模式按幅值有由到小排序，即当i＞j时，Ai≥Aj。

由于实际电力系统中振荡模式众多，故障扰动后的电力系统功率、电压、频率、功角等相关信号，其Prony 分析结果一般有几十个振荡模式。而在几十个振荡模式中有的幅值很小（与最大幅值的振荡模式相比），忽略很小的振荡模式对整个Prony 拟合影响很小。在幅值相对较大的振荡模式中，还可能存在一些振荡模式，忽略它们仅会引起拟合误差的较小或局部的变化。因此，可以将那些对拟合影响较小的振荡模式去除，而保留那些对拟合影响较大的主要振荡模式。

2 识别方法

低频振荡主要振荡模式的识别需要评判去除若干振荡模式的对拟合的影响，提出振荡模式过滤方法，并给出主要振荡模式识别步骤。

2.1 拟合效果评判

对于拟合效果的评判，可以采用误差绝对值的平均值来反映拟合效果。但误差的分布往往是不均匀，使用平均值可能将某段较大误差“平均”掉，出现误差平均值较小而局部误差大的情况，造成将某些主要振荡模式“误去除”的可能。本文将曲线平均分为三段，对每一段分别计算误差绝对值的平均值，可避免主要振荡模式的误去除。

Prony 分析本质上是最小二乘拟合，以保证拟合绝对误差的平方和最小为目标。当信号中的某段曲线值很小、其它段曲线值较大时（如：母线频率偏差，故障后短时间内振荡明显，振荡衰减后趋于0），Prony 拟合的微小误差将造成很大的相对误差，使用相对误差反而不能很好地评判拟合效果。若使用绝对误差评判拟合效果，则评判拟合效果的阈值难以设定。因此，本文对相对误差重新进行定义，以解决前述问题，即：分别计算信号X(n)三段绝对值的平均值，然后再取三个平均值的最大值作为相对误差的分母。设三段拟合误差EX1、EX2、EX3可表示如下：

式3-式5 中K=fix(x)，fix(x)表示对取整。为信号X(n) 平均分为三段后各段绝对值的平均值的最大值，即：

本文评判拟合满足要求为：

式10 中，max(EX1,EX2,EX3) 表 示 取EX1，EX2，EX3的最大值，Eset为拟合效果评判阈值。

2.2 振荡模式过滤方法

振荡模式过滤指将Prony 结果中次要的振荡模式去除，仅保留主要的振荡模式。本文采用两个步骤进行过滤：

1）振荡模式初滤，将Prony 分析结果中“不重要”的后M-H个振荡模式滤除。在M个振荡模式中寻找前H个振荡模式，使得Emax(H) ＜Mset，而Emax(H-1)≥Mset。其 中Emax(H) =max[EX1(H),EX2(H),EX3(H)]，EX1(H)、EX2(H)、EX3(H) 表示仅使用前H个振荡模式计算Prony拟合曲线XM(n) 并计算对应的三段相对绝对值的平均值。

2）振荡模式精滤，在初滤剩余的H个振荡模式中进一步滤除“不重要”的振荡模式。在剩余的振荡模式中，以试错方式逐一删除各个模式，并计算删除振荡模式后的Prony 拟合误差，若满足式10，则该模式不是主要振荡模式，保持删除状态，否则模式是主要振荡模式并恢复。流程如图1 所示。

经过以上两步过滤后保留下的振荡模式均为主要振荡模式。

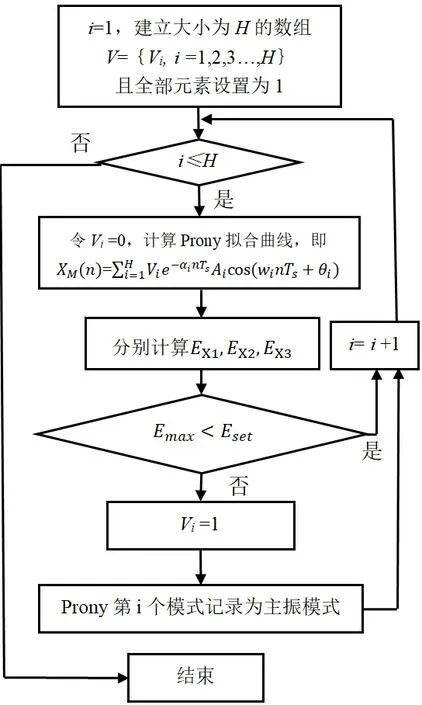
图1 振荡模式精滤流程图

2.3 识别步骤

本文的主要振荡模式识别方法主要包括以下步骤：

1）选择需要识别振荡模式的信号X(n)，对其进行Prony 分析，得到M个振荡模式，并将各振荡模式以幅值从大到小排序。

2）振荡模式初滤。将Prony 分析结果中“不重要”的后M-H个振荡模式滤除，仅保留前H个振荡模式。

3）振荡模式精滤。在初滤剩余的H个振荡模式中进一步滤除“不重要”的振荡模式，保留下的振荡模式均为主要振荡模式。

4）提取满足一定条件的主要振荡模式。当主 要 振 荡 模 式 的 频 率 满 足：wdown≤wi≤wup且Di≤Dup时，将主要振荡模式输出。wdown、wup分别为低频振荡频率范围上下限0.2 ～2.5Hz对 应 的 角 频 率， 即wdown=2×0.2π=1.256，wup=2×2.5π=15.7，Dup为输出阻尼比上限。

3 仿真验证

本文作者将前述的低频振荡主要振荡模式识别方法使用C++语言进行了编程实现。其中，Eset取0.02，Dup取0.08。

某线路故障后有功信号如图2 所示。对3-20秒时间段较为平稳的曲线进行Prony 分析，得到52 个振荡模式，限于篇幅仅列出前20 个幅值最大的振荡模式。使用52 个振荡模式计算Emax(52)=0.13%，表示Prony 分析结果对信号X(n) 拟合很好。经过初滤后，Prony 分析结果中前8 个振荡模式得到保留，使用前8 个振荡模式计算Emax(8)=1.82%。再经过精滤，第6、7 振荡模滤除，使用第1 ～5 及第8 个振荡模式计算Emax(1-5,8)=1.94%。在主要振荡模式中，第2、4、5、8 振荡模式符合输出条件，对其进行输出。软件界面及使用第1 ～5 及第8 个振荡模式对信号X(n)的拟合对比如图3 所示，其中当阻尼比小于0.03 时以红色显示，大于等于0.03 时以蓝色显示。

图2 某线路故障后有功波形

表1 部分振荡模式

图3 Prony分析界面

4 结束语

为克服人工判断主要振荡模式的不足，本文提出了一种电力系统低频振荡主要振荡模式识别方法。首先通过初滤，保留幅值最大的前H 个振荡模式；然后通过精滤，以试错的方式在前H 个振荡模式中进一步滤除非主要振荡模式；最后提取低频振荡范围内的主要振荡模式进行输出，达到电力系统低频振荡识别的目的。本文所提出的识别方法可以准确地识别出主要振荡模式，为动态稳定性的判断提供依据。目前已在云南电网仿真分析中得到了广泛应用，避免了人工识别可能造成的误判。