高温高压下海底管道水平向整体屈曲研究现状分析

刘 润，李成凤

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

自20 世纪70 年代以来，海洋油气资源的开发快速发展．海底管道是海洋油气集输送与储运系统的一个重要组成部分．为了满足生产工艺的要求，海底油气管道内部通常具有较高的输送压力和温度以保障输送介质的流动性．钢质管道在温压联合作用及泊松效应下膨胀，但由于受到地基土体的约束，管道无法自由变形，因而在管壁中产生附加应力，且随着管道长度的增加附加应力不断累积，当累积的应力大于管道临界屈曲荷载时，管道将发生类似于压杆稳定问题的整体屈曲．不可控的整体屈曲会导致管道弯曲截面因应力集中而发生破坏，造成油气泄漏，引起经济损失及安全事故．因此，国内外学者开展了大量的海底管道整体屈曲研究．

根据规范DNVGL-RP-F110[1]，海底管道整体屈曲可表现为水平向屈曲(不埋管道)或隆起屈曲(埋设管道)．早期的海底管道工程多分布在浅海海域，管道以埋设为主，因此管道整体屈曲的研究集中在隆起屈曲．随着海洋油气开发向深海发展，深海管道多裸置于海床上，更易发生水平向整体屈曲．因而自2000年后，海底管道的整体屈曲研究重点逐步向水平向转移．例如，Boreas 咨询公司、TWI 和剑桥大学于2002年共同开展了SAFEBUCK 项目，对管道水平向整体屈曲开展了系统的研究[2-5]．截至目前，海底管道水平向整体屈曲的研究可分为整体屈曲机理、影响参数分析、工程案例和防护措施等几个方面．

最早的理论研究见于1984 年Hobbs[6]推导的刚性地基上理想海底管道发生水平向整体屈曲的解析解及1989 年Hunt 等[7]给出的柔性地基上具有抗弯刚度的弹性杆件的整体屈曲控制方程，这两个理论解成为该领域理论研究的经典，此后海底管道整体屈曲的理论研究皆以此为基础．1993 年，Raoof 等[8]首次发表了管道热屈曲小比尺试验研究成果，随后众多研究人员开展了管道在热应力作用下的整体结构响应以及管道整体屈曲过程中管土相互作用试验．近40年来，海底管道整体屈曲的有限元分析方法得到了较快的发展，SAFEBUCK[2]中指出，数值模拟方法对海底管道整体屈曲的理论研究及工程应用具有重要意义．海底管道整体屈曲的理论研究与数值模拟揭示了管道水平向屈曲的规律性，从而为提出控制管道发生整体屈曲的工程措施提供了可能．2005 年，SAFEBUCK[2]中提出了深海管道水平向屈曲防护的设计思想和初步方案，相关屈曲防护措施也相继在实际工程中得到了成功应用．

本文分别从理论研究、模型试验、数值模拟及防护措施几方面详细阐述这一问题的国际研究现状，并提出该领域未来的研究方向．

1 理论研究

1.1 水平向整体屈曲的机理

管道在高温高压下会产生热膨胀，但是受到地基土的约束力，管道无法自由变形，从而在管壁中产生轴向压力，描述这一过程的管道轴力分布[9]见图1．

图1 中的红虚线描述了管道两端被完全约束时的管内轴力分布．此时，管内轴向压力随温压荷载的升高不断累积至设计温压下的最大轴向压力Po[6]．

式中：A为管道截面面积；E为弹性模量；α为材料的线膨胀系数；T为温压联合作用下的等效温差．

图1 中的黑虚线描述了两端自由管道的轴力分布．管道在温压作用下向自由端膨胀，进而激发地基土对管道的轴向约束力，且该约束力随距管端距离的增加而累积，导致管道轴力从端部开始线性增加，若管道足够长，轴力将沿管道增加至最大轴向压力oP ．

图1 屈曲管道有效轴力分布示意Fig.1 Axial forces in buckling pipes

图1 中的蓝实线描述了管道发生屈曲后的管内轴力分布．根据文献[6]的研究，当管道的轴向压力达到临界屈曲轴力时，管道将发生类似于压杆稳定的整体屈曲(见图1)．管道通过屈曲变形释放其内部轴力，进而使屈曲变形段相邻的管段发生朝向屈曲段的膨胀以释放轴力，称为滑移段．滑移段管道轴力曲线的斜率由土体轴向约束力确定，滑移段长度取决于土体对管道约束力的大小，在滑移段末端形成虚拟锚固点．

图1 展示了单个屈曲的形成及轴力发展过程，而对于较长的管道，可能发生多个屈曲[9]，如图2 所示.

图2 管道发生多个屈曲的轴力分布示意Fig.2 Axial force of pipes with multiple buckles

图2 中的管道共产生了3 个屈曲(实际工程中屈曲的数量因具体工况而异)．由图可知，在两个相邻的屈曲之间存在虚拟锚固点，且虚拟锚固点两侧的管道膨胀方向相反；虚拟锚固点将管道分割成3 个具有独立屈曲的短管；两个屈曲之间的管段以虚拟锚固点为分界点分别发生朝向相邻屈曲的轴向膨胀．在DNV 规范中，将两相邻屈曲共享它们之间管段的轴向膨胀现象称为膨胀共享[1]．

1.2 刚性地基上水平向整体屈曲的理论研究

近40 年来海底管道水平向整体屈曲的解析解取得了很多研究成果．根据剑桥大学 Maltby[10]和Miles[11]的博士论文，海底管道水平向整体屈曲的解析研究可以归纳为两大类：基于刚性地基的解析解与基于柔性地基的解析解．其中基于刚性地基的解析解是将管土相互作用简化为库仑摩擦，将管道视为无限长的欧拉梁，土体对管道的约束力由管道质量和管土间摩擦系数决定，与管道位移无关．

1) 理想平直管道的经典解析解

Hobbs[6]于1984 年最早建立了刚性地基上理想平直管道水平向整体屈曲的解析解，创新性地提出了管道水平向整体屈曲的变形模态(如图3 所示)，给出了各屈曲变形模态管道屈曲力、屈曲幅值和弯矩的表达式，为管道热屈曲的研究奠定了基础．

图3 Hobbs解析解中管道水平向屈曲模态Fig.3 Lateral buckling modes of pipeline by Hobbs

Hobbs[6]认为1 阶模态的水平向整体屈曲控制方程与Hobbs[12]1981 年建立的隆起屈曲的控制方程一致．管道屈曲段的受力分析[12]如图4 所示．

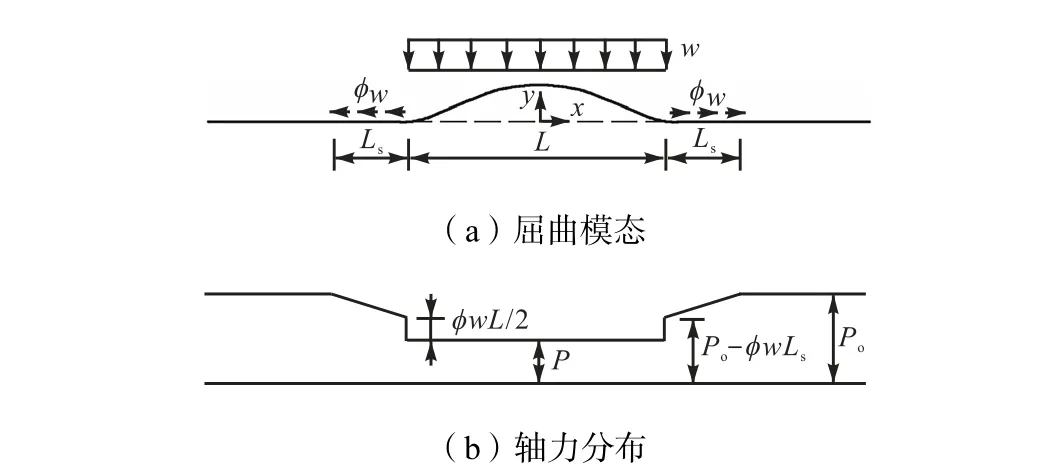
图4 理想长直管道隆起屈曲模态Fig.4 Upheaval buckling mode of a perfect pipe

图4 中假设管道轴力P在屈曲段不沿管道长度而变化，管土相互作用采用库仑摩擦模型且不随管道屈曲位移的变化而改变．通过受力平衡分析及压杆稳定原理建立了2 阶微分控制方程，即

式中：m＝w/EI；n2＝P/EI．其中，w为管道单位长度的浮容重，I为管道横截面的惯性矩，P是管道屈曲

段轴力．

结合图3 中5 种屈曲模态的边界条件，求解管道屈曲段的轴力、最大屈曲幅值以及最大弯矩值，即

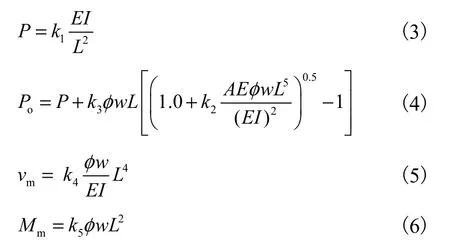
式中：φ是管土间摩擦系数；k1～k5是随管道屈曲模态变化而变化的系数．

2) 具有初始缺陷管道的经典解析解

实际工程中，管道在制造、铺设及运行过程中会因风、浪、流载荷作用、海床不平坦以及渔业活动等因素而产生初始的挠曲．因此，部分学者在理想平直管道理论解的基础上，针对具有初始几何缺陷的管道开展了整体屈曲研究，并提出管道在小缺陷情况下会发生“动态跳转”(snap-through)现象．

Taylor 等[13]于1986 年建立了单拱缺陷及双拱缺陷的管道整体屈曲解析解，单拱缺陷管道的一阶屈曲模态[13]如图5 所示．该解析解被认为是初始缺陷管道水平向整体屈曲的经典解．

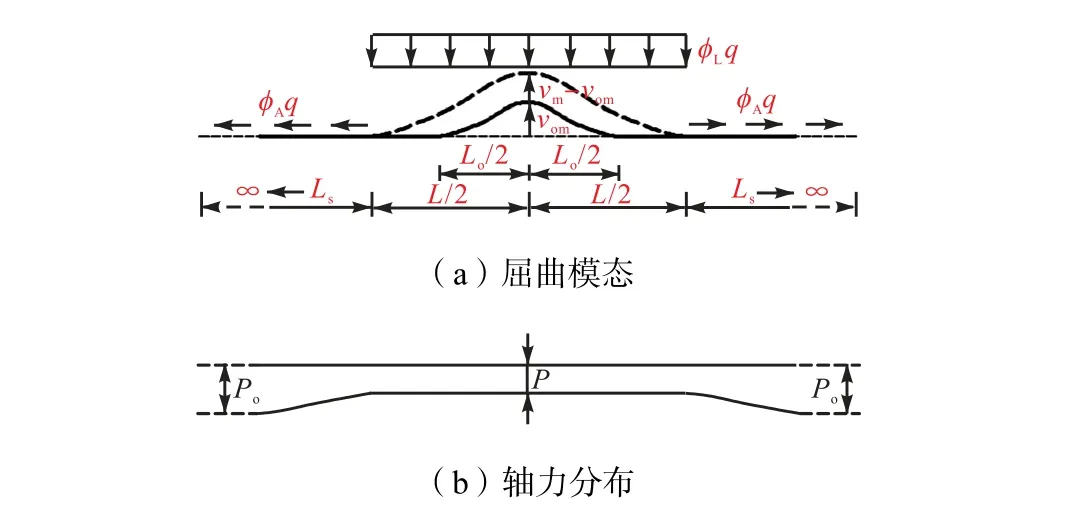
图5 单拱缺陷诱发1阶模态屈曲Fig.5 Buckling of mode 1 induced by a single-arch imperfection

Taylor 等[13]在解析解中假设管道屈曲后的形态相似于其初始几何缺陷，而初始缺陷的形态由Hobbs解确定，即

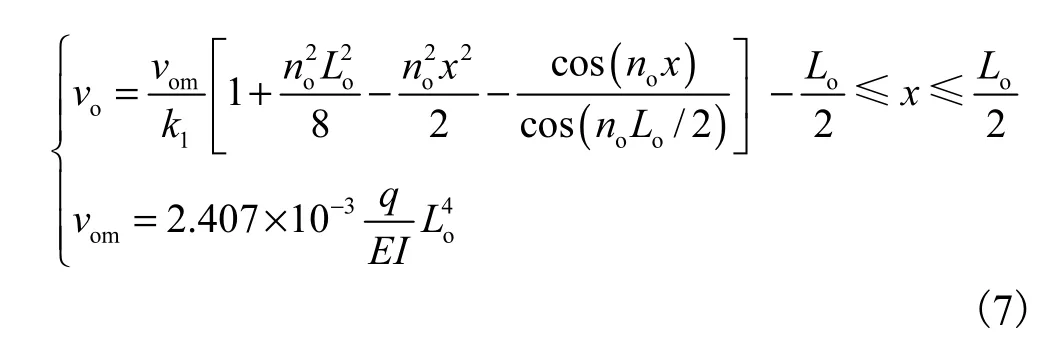
式中：vo为x轴任意位置上管道初始缺陷偏移量；vom为最大初始缺陷幅值；Lo为管道初始缺陷波长；

noLo=8.986 8；q为单位管重．

进而根据管道变形前后能量平衡得到积蓄的应变能V和变形幅值v、初始缺陷幅值v0的关系，由dv/dm＝0 得到屈曲轴力P的表达式为

Taylor 等[13]根据解析解绘制了具有不同初始缺陷管道的屈曲轴力，研究了缺陷对管道整体屈曲的影响，发现管道屈曲临界轴力随缺陷的减小而增大，当缺陷很小时，会出现“动态跳转”(snap-through)现象.

3) 其他解析解研究

国内外大量学者在理想管道及缺陷管道解析解的基础上，对刚性地基上水平向整体屈曲解析解进行了更加深入的研究．较为典型的有天津大学刘润，先后基于静力平衡法[14]和能量法[15]推导了理想管道发生高阶屈曲(图3 中的模式3 和模式4)的解析解，并对初始缺陷管道的高阶整体屈曲进行了系列的研究．例如，Hong 等[16]提出管道的屈曲形态并不完全

相似于其初始缺陷，而是发生3 阶模态屈曲变形，并

基于能量法推导了该屈曲模态的解析解．Liu 等[17]基于静力平衡方法对具有单拱对称和双拱反对称初始缺陷的管道建立了高阶水平向整体屈曲的解析解.

初始缺陷显著影响管道整体屈曲的临界轴力[13].1999 年，Sriskandarajah 等[18]分析了海底管道水平向整体屈曲受几何初始缺陷的影响规律，并求解了不同初始缺陷下管道整体屈曲的临界轴力．2010 年，刘羽霄[19]采用能量法推导了几何缺陷管道水平向整体屈曲临界轴力的解析解，并通过有限元方法进行了验证．Zeng 等[20]和Xu 等[21]采用无量纲分析方法推导了考虑初始缺陷形状、尺寸以及初始缺陷幅值和波长的比值vom/Lom等参数的临界轴力计算公式，量化了初始缺陷各参数对管道屈曲的影响．

1.3 柔性地基上水平向整体屈曲的理论研究

1) 4 阶微分控制方程

刚性地基上管道水平向整体屈曲的解析解基于管土间库仑摩擦的假定，即将土体对管道的约束力视为常数．但在实际工程中，管土间的相互作用具有明显的非线性[22]，且与管-土的相对位移相关联．因此为了考虑土体对管道约束力的非线性，将管道分解为微单元进行受力分析[23]如图6 所示．基于图6 可得到描述管道整体屈曲的4 阶微分控制方程[24]为

式中：y为屈曲位移；F(y)为土体对管道约束力的非线性函数．

大量学者在式(9)中引入了一次至三次函数或指数函数来模拟管土相互作用，但由于高阶微分方程求解困难，各种近似求解方法得到了应用，例如非线性摄动法、伽辽金法和打靶法等．

2)F(y)＝ky-cym土体约束力模型的管道水平向整体屈曲近似解

Hunt 等[7]于1989 年研究了柔性地基上弹性杆件的整体屈曲问题，为柔性地基上管道的热屈曲研究奠定了基础．该研究假定土体对管道约束力方程为

F(y)＝ky-cym，代入式(9)可得

式中k和c为常系数．

Hunt 等[7]针对m＝2 的形式，基于非线性摄动法求解了控制方程(10)，将其展开为一组由多个线性微分方程组成的有序序列，即

式中s是一个从零开始随着远离临界点C而增长的扰动参数

将式(11)代入控制方程(10)，并将s，s2，…的系数依次设为零，可得关于y1(x，X)，y2(x，X)，…的一系列线性微分方程，进而得到整体屈曲数值解

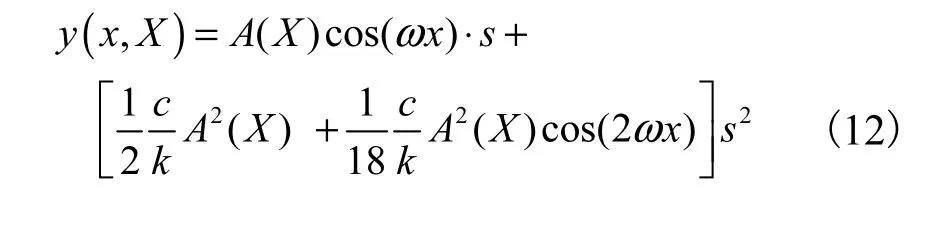
对于土体约束力形式为F(y)＝ky-cym的屈曲控制方程，后续研究还见Hunt 等[26]于1996 年推导的m＝3 时整体屈曲的近似解；Whiting[27]于1997 年采用伽辽金法推导的m＝3 时整体屈曲的近似解；Zeng 等[28]于2014 年同时推导了m＝3 和m＝5 时管道整体屈曲的近似解．

3) 其他土约束力模型的管道水平向屈曲近似解

除了F(y)＝ky-cym形式的土体约束力模型外，其他诸多非线性土体约束力模型也被应用于管道整体的屈曲分析中，例如指数型土体约束力模型．1995年，Maltby 等[29]基于Tvergaard 等[24]的研究成果，将指数模型F(y)＝Q0(1-ey/Δ)(Q0为土抗力最大值，Δ为Q0所对应的管道位移)引入管道屈曲控制方程，推导了具有初始缺陷的管道整体屈曲的数值解，并进行了模型试验验证．2012 年，Lagrange 等[30]基于双线性和指数型两种非线性土体约束力模型建立了管道状态屈曲控制方程，采用伽辽金和数值解法求解了具有初始缺陷的弹性梁的整体屈曲，并研究了初始缺陷大小对整体屈曲特征的影响．2013 年，Karampour等[31]推导了指数型土体约束力模型下海底管道水平向整体屈曲数值解，研究了初始缺陷形状对整体屈曲特征的影响．

近年来，出现了更多形式的土体约束力模型及管道整体屈曲控制方程的求解．例如，2015 年，Zhu等[32]基于轴向和水平向双曲正切函数形式的土体约束力模型，推导了理想管道水平向屈曲的解析解，并对管道临界长度进行了研究，指出当管道长度大于或等于临界长度时，管长增加或边界条件变化不会影响管道的整体屈曲行为．2017 年，Wang 等[33]基于Chatterjee 等[34]建立的土体约束力模型，采用打靶法推导了半埋理想管道对称和反对称水平向整体屈曲的解析解，并与 Hobbs[6]的经典解析解进行了对比．2017 年，Wang 等[35]采用摄动法求解了非线性土体约束力模型下缺陷管道整体屈曲的近似解，研究了土体特性及初始缺陷对管道整体屈曲的影响规律．

2 模型试验的研究

理论研究是对管道整体屈曲的力学描述，在求解理论解的过程中通常需将一些非线性因素进行简化，但这种简化可能对管道整体屈曲响应有重要影响[36]，因此开展模型试验是研究海底管道整体屈曲的有效手段．目前关于海底管道整体屈曲试验研究主要包括两个方面：一是管道在热应力作用下的整体结构响应，二是管道运动过程中受到的土体约束研究．

2.1 管道整体屈曲模型试验

较早的管道整体屈曲试验研究均是针对隆起屈曲进行的，这为水平向屈曲试验研究提供了可参考的经验．1993 年，Raoof 等[8]首次发表了完整的管道整体屈曲试验研究成果，该研究开发了一种能够将管道加热到100 ℃模拟管道隆起屈曲和水平向屈曲的装置，并基于该装置对长7 m、直径16 mm 的铜镍管开展了隆起屈曲试验．此后，Maltby 等[37]在1995 年对长5 m、直径6 mm 的有埋深管道进行了小比尺隆起屈曲试验，该试验通过螺旋布置或内部油压对管道施加轴向荷载．Taylor 等[38]和Moradi 等[39]先后进行了一系列温度荷载下管道隆起屈曲的模型试验．

基于上述管道隆起屈曲试验研究，Miles 等[11,36]采用小比尺模型试验研究了管道水平向整体屈曲规律．试验采用断面为正方形，边长7 mm、总长2 m的硅橡胶条模拟实际工程中的管道，采用尺寸为2.4 m×0.45 m×0.05 m(长×宽×高)的聚苯乙烯板模拟海床，硅橡胶条的热膨胀量通过底板长度方向的压缩量模拟，重点研究了整体屈曲形成后的发展规律.

2004 年，Poiate Junior 等[40]开展了普通单层管和Z 形铺设管的水平向整体屈曲模型试验，试验布置[40]如图7 所示．试验中所用管段以1∶6 的几何缩尺模拟原型管道，模型管长16 m，管径76.2 mm，壁厚2 mm．试验所得的管道水平向整体屈曲变形结果和数值结果差异约为5%，呈现较好的一致性．

图7 水平向整体屈曲模型试验布置Fig.7 The general view of the experimental apparatus

2008 年，Silva-Junior 等[41]开展了考虑枕木作用及分布浮力作用的管道整体屈曲缩比尺模型试验，将不同构型的人为屈曲触发因素应用于195 m 长的模型管道(原型管道长5 850 m)，并基于设计条件施加温度荷载，在模型管道发生整体屈曲过程中测量各截面的应变、温度、压力和位移．该试验是已有报道中尺寸最大的管道整体屈曲模型试验．

由于开展管道整体屈曲的模型试验设备复杂、费用昂贵、测试难度大且存在尺寸效应等，因此现有模型试验成果较少，仅有的试验数据为揭示海底管道整体屈曲的机理，研究其屈曲发展过程提供了重要的数据来源．总结现有的管道整体屈曲试验研究成果可知，管道整体屈曲试验的关键在于：①正确地选择模型试验材料及对应的模型管道长度和管径；②设计精确可控的加荷系统．

2.2 管土相互作用试验

管土相互作用的试验研究分为以下3 个阶段：①库仑摩擦模型阶段，这个阶段均采用库仑摩擦模型计算土体对管道的约束力；②土压力模型阶段，即将水平向土抗力分为摩擦抗力和被动土抗力两部分进行计算；③土拱模型阶段，即土体对管道约束力的分析考虑了大位移条件下土拱作用的影响．

在海底管道应用之初，往往将水平向土抗力简化为摩擦抗力，采用库仑摩擦模型计算土体对管道的约束力．因此，学者们开展管土相互作用试验以确定管道设计中的土抗力系数．最早的试验研究见于1973年，Lyons[42]针对不同土性中不同直径及表面涂层的管道，开展了水平向位移下的土抗力试验，发现砂土中轻管道的摩擦系数为常数，而黏土中管道的摩擦系数随管道浮容重、直径及其表面粗糙度的变化而变化，因此库仑摩擦模型仅适用于砂土地基上的轻管.1981 年，Anand 等[43]开展了小比尺、大比尺模型试验及现场试验，分析了细砂、粗砂及粉土地基上水平向位移管道的摩擦阻力．1986 年，Brennodden 等[44]开展了松散细砂、中粗砂、软黏土和硬黏土地基上管道水平向土阻力的原比尺试验，试验结果显示砂土中管道摩擦系数在0.70～1.25 间变化，并最终确定为0.75.

随着海底管道的广泛应用和深入研究，发现管土相互作用是一个复杂的非线性过程，简单的库仑摩擦理论不能反映管道运动过程中所受的非线性土体约束力．1989 年，Wagner 等[45]在PIPESTAB 项目的支持下，分别开展了砂土和黏土中管道在不同加载形式下的水平向运动试验，并基于试验结果建立了土体对水平向运动管道约束力计算公式，将土体约束力划分为库仑摩擦抗力和被动土抗力两部分，即

式中：Ff为库仑摩擦抗力，等于有效竖向荷载与摩擦系数的乘积；FR为被动土抗力，与管前土拱体积有关.

挪威船级社于2007 年颁布的DNV-RP-F109[46]规范采用了将管道水平向土抗力分为摩擦力和被动土抗力两部分的方法，并将被动土抗力随管道位移而变化的过程定义为四段式土抗力模型．

随着海洋工程向深海发展，海底管道水平向整体屈曲逐渐成为管道安全性的重要控制因素，众多研究者针对管道水平向屈曲时的大位移运动开展了管土相互作用模型试验研究．2006—2008 年，Bruton等[3,47-48]在SAFEBUCK JIP 项目的支持下，针对墨西哥湾和西非的深水土体开展了浅埋管道水平向管土相互作用的大比尺、小比尺试验和离心机试验．根据管道水平向整体屈曲的发展规律，对安装过程中管道沉降阶段、管道在屈曲形成过程中经历破土抗力及吸附力消散阶段、管道整体屈曲过程中首次经历水平向大位移阶段、受土拱影响的管道水平向循环位移阶段共4 个阶段进行了研究．发现管道在水平向大位移过程中，受到的土阻力在达到峰值后呈现出两种不同的变化趋势，据此提出了“轻管”与“重管”的概念，并针对“轻管”建立了包含以上4 个阶段的管土相互作用模型．

作为SAFEBUCK JIP 项目的重要成员，剑桥大学在管土相互作用研究领域占有重要地位．2007 年，Cheuk 等[49]在剑桥大学开展了针对西非黏土以及墨西哥湾软黏土的管土相互作用原比尺试验．根据试验现象将管道在地基中水平向运动的土阻力-管道位移响应确定为以下4 个阶段：破土、吸附力消散、稳定增长的土拱抗力、预先存在的休眠土拱的附加抗力，并提出了一个简单的上限解来模拟上述4 个阶段的试验响应，这是对海底管道水平向大位移中土抗力响应机理的首次定量建模，该模型考虑了土拱的增长过程．

2008—2011 年，西澳大学 White 等[50-51]和Dingle 等[22]在Cheuk 等[49]试验的基础上，通过离心机试验模拟了软黏土地基上海底管道发生水平向循环大位移的情况，并采用PIV 技术观测了管道水平向运动时的土体速度矢量，揭示了软黏土地基上管道沉降和水平向破土抗力的发展过程和机理．

2017 年，DNV 颁布的DNVGL-RP-F114[52]规范吸纳了SAFEBUCK JIP 项目以及该项目中各成员的最新研究成果，收录了大位移及循环工况下考虑土拱作用的复杂管土相互作用模型，提出排水条件下管道的破土抗力可以分为摩擦力、被动土抗力和考虑土拱作用的附加抗力3 部分，其中摩擦力、被动土抗力有较成熟的计算公式，而考虑土拱作用的附加抗力的计算有待进一步研究．

国内关于海底管道的研究起步较晚，从2011 年至今，天津大学岩土所开展了一系列管土相互作用的研究工作．2011 年，刘润等[53]通过模型试验研究了渤海湾细砂地基上不同直径、不同埋深的管道发生竖直向、水平向以及轴向运动时土体抗力的发挥过程，提出了渤海中管道所受土体约束力的经验公式．2015年，Liu 等[54]针对渤海湾软黏土地基中的管道开展了轴向及竖直向管土相互作用试验，并通过对试验数据的分析提出了渤海软黏土轴向和竖向非线性管土相互作用模型．2016 年，Wang 等[55]针对直径16 cm、不同管重、不同埋深的管道开展了砂土地基上水平向管土相互作用试验，对管道水平向大位移过程中管前土拱的形成和发展机制进行了研究．2018 年，Wang等[56]针对不同重量管道的浅埋情况，开展了管道水平向大位移运动模型试验，分析了砂土海床上水平向土抗力随管道运动的发挥机制以及管道水平向失稳时管前土拱的变形规律．并应用极限分析理论中的上限法获得了管道水平向破土抗力的计算方法．

综上所述，众多研究者针对管道水平向整体屈曲时的大位移运动开展了管土相互作用模型试验研究，不同性质土体对管道约束力均呈现出显著的非线性和依赖于应力路径的复杂性，精确地描述土体对水平向大位移管道的约束力发挥过程，特别是针对“重管”的土抗力模型还需要大量的研究和实践．

3 数值模拟研究

模型试验虽然可以直观地展示管道在高压高温下的整体屈曲响应，但是缩尺效应不容忽视．例如，实际工程中管道的整体屈曲波长可达24～70 m，幅值可达0.5～2.0 m，远远大于模型试验的尺寸．因此，随着数值模拟技术的快速发展，近40 年以来基于PIPLIN-III、PLAXIS、ANSYS 以及ABAQUS 有限元软件的分析方法被广泛应用于海底管道整体屈曲研究中，提出了可模拟管道整体屈曲的数值方法，并对管道整体屈曲进行了参数研究和工程设计指导，在管道整体屈曲的防护研究中也取得了显著效果．

3.1 整体屈曲有限元分析方法

高温高压作用下海底管道整体屈曲是一个复杂的非线性大变形问题，因此，管道整体屈曲数值模拟的关键在于考虑其非线性和大变形，包括管道整体屈曲过程中的大位移和大挠度，升温过程中管道材料的弹塑性特性以及非线性管土相互作用等[57]．

大位移的模拟是管道整体屈曲模拟的关键问题之一．为了模拟非线性大挠度变形行为，目前最常用的方法是位移控制法，即在隐式分析中，通过阻尼器控制结构的稳定位移，并求解不稳定响应段的静力平衡问题．该方法被称为Riks 方法，最初由Riks[58-59]和Wempner[60]提出．Crisfield[61]和Ramm[62]进一步改进和发展了该方法，使其成为分析非线性结构稳定性问题的主要方法，且在有限元软件ABAQUS[63]中内置了改进的Riks 方法．除了改进的Riks 方法外，其他一些方法也被用于非线性屈曲问题的研究中，例如显式动态方法[63]．这是一种加速度控制方法，通过惯性效应控制加速度，并在显式分析中处理结构的稳态位移，从而模拟管道的整体屈曲变形．Riks 方法、改进Riks 方法和动力显式方法均被应用于管道整体屈曲的数值模拟中，例如Sriskandarajah 等[64]、赵天奉等[65-66]、Jukes 等[67]、Sun 等[68]、Liu 等[69]、王立忠等[70]先后对整体屈曲数值模拟的不同方法进行了研究，结果表明Riks 法和动力法均可有效模拟海底管道的整体屈曲．

管土间界面模拟是管道整体屈曲有限元分析中的另一个关键问题．管土相互作用是一个复杂的非线性过程，直接影响了管道的变形和应力分布规律，在管道整体屈曲响应研究中起着重要作用．因此，大量学者对管道整体屈曲中管土相互作用的模拟进行了研究．文献调研显示，管土相互作用的模拟方法主要包括以下4 种．

(1)摩擦定律法．将非线性土阻力简化为一个由管重和摩擦系数确定的常摩擦力．虽然简单的摩擦定律不能反映管道水平向整体屈曲过程中土抗力随管道位移的变化，但它被广泛应用于管道整体屈曲研究中，因为该方法显著降低了管道整体屈曲计算的难度．较早的研究有1973 年，Lyons[42]发现采用有限元方法模拟铺设于砂土上的管道水平向位移时，将管土相互作用简化为传统的库仑摩擦模型是合理的. 2007年，基于 SAFEBUCK JIP 项目，Bruton 等[4]采用ABAQUS 有限元软件分析了水平向土阻力对管道水平向整体屈曲的形态、管道轴力、初始屈曲条件等的影响，分析中将管土间作用力设为库仑摩擦力．其他学者，例如Rubio 等[71]、Walker 等[72]、Haq 等[73]、Liu等[69]，在管道整体屈曲有限元分析中均采用库仑摩擦力模拟管土相互作用．

(2)非线性弹簧单元法．Andreuzzi 等[74]、Zeng等[28]、施若苇[75]以及Liu 等[54]均采用弹性或弹塑性弹簧模拟了管道整体屈曲过程中的土体约束力．这种“弹簧滑块”单元法类似于用于分析桩基响应的t-z和p-y 载荷传递方法，即以基本的管土单元为对象提供一种分析管道轴向和水平向非线性弹塑性响应的研究方法．

(3)PSI 单元法．ABAQUS 中的管土相互作用(PSI)单元可用于模拟管道与周围地基之间的非线性相互作用．相较于与弹簧分布密度密切相关的非线性弹簧单元，PSI 单元以“力/单位长度”作为单元刚度，与分布密度无关，解决了弹簧单元模拟管土相互作用时可能引起的节点处应力集中问题，因此被一些学者用于管道整体屈曲分析中，例如Sun 等[76]、Zeng等[77]、Liu 等[78]．

(4)子程序方法．为了模拟更复杂的管土相互作用，特别是对于管道经历大位移变形的工况，引入子程序成为管土相互作用模拟的另一种有效方法，该方法能够考虑管土相互作用的突变行为以及循环效应．Jukes 等[67]开发了一个可用于模拟管道整体屈曲过程中非线性管土相互作用的高度非线性有限元子程序Simulator，并对实际工程管道进行了整体屈曲的模拟，对海底管道的整体稳定和局部安全进行了分析．刘润等[79]在ABAQUS 中采用子程序VFRIC 模拟管道与地基间的动态非线性相互作用，进而对海底管道整体屈曲进行较精确的分析.

3.2 整体屈曲有限元分析的应用

管道整体屈曲的数值分析方法被广泛用于参数分析[70]，并在实际工程中发挥了重要作用[68,80]．

3.2.1 参数分析

管道整体屈曲的参数分析是指采用有限元方法研究管道直径、长度、初始缺陷、管土相互作用、荷载等相关参数对管道整体屈曲影响的规律性．例如，2010 年，刘羽霄[19]基于ANASY 软件研究了初始几何缺陷、管土间摩擦系数、土体屈服位移、管道径厚比、管材刚度等参数对管道水平向屈曲的影响规律．2010 年，Walker 等[72]利用ABAQUS 建立有限元模型，分析了材料属性、摩擦系数、虚拟锚间距(VAS)对管道整体屈曲最大轴向应变的影响．2013年，Haq 等[73]运用有限元方法研究了管道外径与壁厚的比D/t、管道弯曲度(OOS)、管道内外温差、压差、工作水深以及水平向和轴向摩擦系数对管道整体屈曲的影响．2018 年，Liu 等[81]分析了管道长度对管道整体屈曲的影响规律，发现管道屈曲幅值先随管道计算长度增长非线性增长，在管道长度达到临界值之后保持恒定．在以上所有参数中，管道整体屈曲的主要控制变量可概括为管道中的轴力、初始缺陷与管道所受约束力[2]，其中初始缺陷是管道发生整体屈曲的诱因，管道受到的土体约束力最为复杂．

1) 初始缺陷的影响研究

1999 年，Torselleti 等[82]在Hotpipe JIP 项目的支持下研究了初始缺陷对海底管道水平向屈曲的影响规律，有限元计算结果显示管道后屈曲响应几乎不受初始缺陷幅值的影响，而管道整体屈曲临界轴力及“动态跳转”现象受管道初始缺陷影响显著，较小的初始缺陷幅值(较低的初始缺陷曲率)会产生较高的“动态跳转”屈曲的临界轴力．刘羽霄等[83]基于ANSYS 软件对初始缺陷幅值及波长影响管道前屈曲及后屈曲的研究结论与Torselleti 等[82]一致，即初始缺陷对管道屈曲临界温差有显著影响，但对管道后屈曲的变形、弯矩、轴向应变影响较小．

1999 年，Sriskandarajah 等[18]指出有限元方法能有效分析初始缺陷对管道整体屈曲的影响，管道整体屈曲临界轴力随初始缺陷幅值与波长的比值增大而减小，且管道屈曲模态并不像Taylor 等[13]所假设的那样相似于其初始缺陷，而是会随着屈曲的发展而变化.

2004 年，Villarraga 等[84]利用数值计算方法研究了含初始缺陷管道的整体屈曲变形过程，发现初始缺陷对管道应力分布有较大影响，在某些情况下会导致应力超过设计规范规定的允许极限．2006 年，Suzuki等[85]研究了几何缺陷对管道整体屈曲的影响，认为管道的抗弯承载力与几何初始缺陷无关，而应变易受几何缺陷的影响．2008 年，Rathbone 等[86]运用有限元法研究了缺陷半径和弧长对管道整体屈曲的影响，并提出了一种管道弯曲的评估方法. 2015 年，Hong等[87]研究了具有不同初始缺陷管道的失效包络线，分析了初始缺陷对管道安全性的影响．2018 年，Liu等[88]发现包括管道弯矩、应变、横向位移等在内的后屈曲特征值均随缺陷幅值增大呈现先增大后减小的趋势．

综上所述，初始缺陷对海底管道整体屈曲的影响包括对前屈曲的影响及后屈曲的影响．对前屈曲的影响主要体现在影响管道整体屈曲的临界轴力或温差，研究表明管道屈曲临界轴力随着初始缺陷幅值的增加而减小，且与初始缺陷的形态相关，当初始缺陷幅值很小时，会出现“动态跳转”现象；对后屈曲的影响可以概括为两点：一是对管道变形幅值和屈曲模态的影响，二是对管道屈曲变形过程中弯矩、应力、应变的影响，最终体现为对管道失效概率的影响．管道初始缺陷对管道后屈曲的影响的研究结论不一，甚至存在矛盾，有待进一步完善．

2) 土体约束力的影响研究

有限元方法的应用使得土体约束力对管道整体屈曲影响规律的研究取得了重要进展．2006 年，Cardoso 等[89]在管道水平向屈曲有限元分析中考虑了土拱作用，发现土拱的存在对管道整体屈曲的变形过程、管壁材料的应力和应变行为均有显著影响.2007 年，Bruton 等[4]研究了轴向和水平向土体约束力对管道轴力、管端膨胀、管道整体屈曲启动条件、屈曲荷载以及屈曲管段稳定性的影响规律，结果表明土体约束力的影响具有双面效应，例如，较大的土体阻力可在一定程度上限制管道发生整体屈曲，但会增加屈曲力．

2010 年，Walker 等[72]研究了沿管道分布的不对称摩擦力对管道整体屈曲的影响，结果表明较小程度的不对称侧摩阻力会导致整体屈曲变形和应变的显著不对称．2011 年，刘羽霄等[90]研究发现管道整体屈曲的临界温差、最大弯矩及最大轴向总应变随着水平向摩擦系数的增大而增大，但受轴向摩擦系数影响不明显．2013 年，Haq 等[73]研究发现整体屈曲管道的有效轴力和应变均随着管土摩擦系数的增加而增加．

2018 年，Liu 等[78]基于DNV-RP-F109[46]所给出的非线性管土相互作用模型，分析了相关参数对管道水平向整体屈曲的影响，发现管土相互作用模型中的最大土阻力、残余土抗力以及最大土阻力对应的启动距离均对管道整结体屈曲影响显著．同年，李成凤等[91]的研究表明管土间摩擦力对管道整体屈曲的影响规律与管道长度有关，发现长管的整体屈曲幅值随土体约束力的增加而减小，而短管的整体屈曲幅值随土体约束力的增加呈现先增加后减小的趋势．

由此可见，管道屈曲的形态和内部轴力分布与土体对管道的约束力密切相关，全面揭示这一过程的复杂性和非线性是海底管道水平向整体屈曲研究的方向之一．

3.2.2 工程应用

海底管道的数值模拟方法在实际工程中得到了应用，并用于指导海底管道整体屈曲的防控设计．

2002 年，Zhang 等[92]采用基于ANSYS 的三维有限元方法，对挖沟但未埋设的15.24 cm(6.0 in)海底管道的整体屈曲进行了工程案例分析，分析中采用了非线性弹簧单元模拟管道和回填土之间的相互作用.

2003 年，Harrison 等[80]阐述了位于墨西哥湾密西西比峡谷区域名为King 的海底管道的设计历程，采用ABAQUS 有限元分析软件，结合传统的解析解，对长27 km、安装于水下1 625 m 的King 管道的防护措施进行了研究．评估了蛇形铺设、轨枕以及分布浮力法对管道水平向整体屈曲响应的影响，研究认为枕木法是最适用于该工程的管道整体屈曲防护方案，进而采用有限元方法进行了详细的设计和评估．

2009 年，Jukes 等[67]概述了海底管道整体屈曲及局部结构屈曲响应的有限元分析方法的最新进展，并总结了这些方法在管道设计中的应用，详细介绍了考虑管土非线性的有限元程序Simulator 在海底管道整体屈曲分析中的应用，并指出该有限元程序已成功应用于多条海底管道工程中的整体屈曲分析和评估．

Jukes 等[93]、赵天奉等[65]、Carpenter[94]分别就墨西哥湾、惠州、中国南海管道工程进行了大量的数值模拟，且诸如Penguins[95]、Greater Plutonio[96]、Tahiti[97]等管道工程也采用了有限元分析方法进行设计．

大量实际工程应用验证了有限元方法在模拟和预测管道整体屈曲中的有效性和先进性．有限元分析方法已成为海底管道整体屈曲设计的有效工具．

4 屈曲防护研究

整体屈曲会导致管道内的应力-应变随温度的升高而累加，造成屈曲破坏或者疲劳效应，因此屈曲防护是海底管道整体稳定设计中的关键．文献调研与工程实践表明，现有的海底管道整体屈曲防护措施可分为两大类：一是通过减小温压荷载、增加管道抗弯刚度或海床约束力以达到完全消除管道整体屈曲的目的，称之为“避免屈曲”防护措施；二是通过在预定位置引入屈曲诱发因素，促使管道发生可控的整体屈曲，称之为“控制屈曲”防护措施．其中控制屈曲是一种适用于深海管道且相对经济高效的屈曲防护方案，SAFEBUCK JIP 项目[2]列举了常用的3 种整体屈曲诱发方式，即蛇形铺设法、枕木法和分布浮力法．

4.1 蛇形铺设法

蛇形铺设法是指管道以设计路由为中心线、以给定幅值有规则地偏移铺设．该方法的原理是通过在预定位置设置一系列水平向初始缺陷来诱发管道发生可控的整体屈曲．蛇形铺设法诱发管道整体屈曲的关键参数是蛇形铺设间距、偏移幅值和铺设弯曲半径，其铺设方案及各参数典型值域如图8[2]所示．

图8 蛇形铺管示意Fig.8 Typical snake-lay configuration

Sinclair 等[98]在SAFEBUCK 项目支持下公布了3 个典型蛇形铺设管道工程实测数据，展示了蛇形铺设方案在管道实际工程中的成功应用．其中位于北海北部的“Penguins”工程是蛇形铺设的一个典型案例，该管道长60 km，设计温度110 ℃，内压39 MPa，采用间距2 km、半径1 500 m、弧长300 m 的蛇形铺设方法．2004 年，Matheson 等[95]概述了在设计阶段对“Penguins”管道蛇形铺设效果进行预测的方法，并将预测结果与实际管道运行期间的观测结果进行了比较．同年，Peek 等[99]和Carr 等[100]采用有限元分析、大比尺试验和实际工程分析相结合的方法对“Penguins”管道的蛇形铺设方案进行了综合评估.2009 年，Sinclair 等[98]给出了“Penguins”管道的监测数据，显示25 个蛇形铺设中24 个产生了横向弯曲.这展示了蛇形铺设方法在管道屈曲防护设计中的可靠性．

Preston 等[101]、Rundsag 等[102]、Hooper 等[103]先后采用有限元方法分析了蛇形铺设法中几何形状对管道整体屈曲临界轴力、后屈曲弯矩及应力的影响规律．2010 年，刘羽霄[19]提出了一种新的蛇形铺管形状，研究了蛇形铺管半径、铺设长度和铺设角度对管道整体屈曲的影响，并针对蛇行铺设法中存在的问题，提出了蛇形铺设法与枕木法联合的管道整体屈曲诱发方式．

4.2 枕木法

枕木法是指在管道路由的特定位置设置枕木，使管道在枕木的位置形成初始缺陷和悬跨段，激发管道在温压联合作用下发生整体屈曲．枕木方案的关键控制因素是枕木高度及相邻枕木间距，其铺设形态及各参数典型值域[2]如图9 所示．

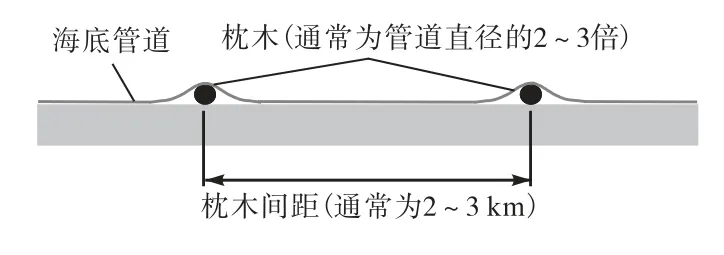
图9 枕木法示意Fig.9 Buckle initiation using sleepers

最早在实际工程中应用枕木法的报道见于位于墨西哥湾密西西比峡谷的名为King 管道．该管道长27 km、安装于1 625 m 的水下．2003 年，Harrison等[80]针对King 管道，详细描述了枕木法的设计步骤、枕木高度及距离等参数的确定过程，并给出了管道在安装、试运行及运行过程中的声纳扫描数据，验证了枕木能较好地在预设位置激发管道整体屈曲．

Jayson 等[96]对2007 年10 月投入运营的大普鲁托尼奥油田(Greater Plutonio Project)管道的整体屈曲防护设计和实施效果进行了阐述．该工程采用枕木法作为管道整体屈曲触发装置，并通过对枕木两侧管段增加绝缘涂层厚度来提高局部附加浮力的方法，增加管道的整体屈曲波长，达到减小屈曲段管道局部应力的目的．Jayson 称这是世界上第一个采用浮力和枕木相结合的措施控制管道整体屈曲的工程．

2009 年，Carneiro 等[104]概述了巴西利亚北部海岸圣埃斯普利托盆地(Esprito Santo Basin)1 500 m 水深下的两条输油管道的整体屈曲防护方案．该管道直径219 mm、长度6 km．通过分析发现单枕木法或分布浮力法的可行性均较差，最终确定了采用间隔1.3～2.0 km 的双枕木法．

2009 年，Sinclair 等[98]给出了9 条采用枕木法触发管道整体屈曲的工程实测数据，集中展示了枕木法在多个实际管道工程项目的成功应用．

4.3 分布浮力法

分布浮力法是指在管道路由的特定位置安装浮力块，降低管道的浮容重，减小管道所受的土体约束力以激发管道在温压作用下发生整体屈曲．分布浮力法的设计关键是浮力块作用段管道浮容重的降低比值、浮力块长度和分布浮力块的间距．Sinclair等[98]指出浮力作用段管道的浮容重可降低至正常管段浮容重的10%～15%，典型浮力块长度和间距见图10．

图10 分布浮力法示意Fig.10 Pipeline with distributed buoyancy

2007—2008 年，分布浮力法成功应用于墨西哥湾的“Tahiti”管道系统．2009 年，Thompson 等[97]概述了“Tahiti”管道系统采用分布浮力法诱发管道整体屈曲的设计方案，并采用ABAQUS 对该方案的实施效果进行了详细的分析和预测．

分布浮力法虽然在几个海底管道工程中得到了应用，但相关的实测数据在已有报道中较少，大多为理论研究．例如，Peek 等[105]、Antunes 等[106]先后推导了分布浮力单元作用下管道水平向屈曲的解析解，并采用有限元方法进行了验证．2012 年，Sun 等[107]通过试验和有限元方法对比分析了分布浮力法和枕木法在管道整体屈曲防护中的应用效果，认为在海床特性未知的条件下，分布浮力法比枕木法具有更好的适用性．2016 年，战立超[108]揭示了管道在分布浮力作用下发生水平向整体屈曲的机理，并基于分布浮力作用下海底管道水平向整体屈曲的失效模式提出了分布式浮力装置的布置准则和优化设计方式．

综上所述，海底管道整体屈曲的防护措施旨在实现对管道整体屈曲的有效控制．已有防护措施在多个深水管道项目中的成功应用，证明了人为干预整体屈曲的可行性与可靠性．

5 展 望

本文通过文献调研详述了近40 年来国内外在海底管道水平向整体屈曲研究领域的重要成果．这些成果涉及管道整体屈曲的机理、整体屈曲的影响因素及规律性、整体屈曲的理论及数值分析方法以及整体屈曲的防护措施和工程应用进展．众多研究成果真实地展示了海底管道水平向整体屈曲研究和应用的发展历程，揭示了这一问题的复杂性和多学科交叉特点，也为今后的研究指明了方向．

1) 理论研究方面

目前的海底管道整体屈曲理论研究中，采用的2阶微分控制方程不能考虑非线性管土相互作用，而考虑了非线性管土相互作用的4 阶微分控制方程没有严格的解析解．因此，建立能考虑非线性管土相互作用且能求解出管道整体屈曲幅值和弯矩的解析方法是海底管道整体屈曲理论研究应解决的问题．

此外，现有管道整屈曲的解析解均假设管道无限长，即滑移段末端的轴力为完全约束轴力，适用于长管．对于设置了整体屈曲诱发装置的管道，多个整体屈曲间的虚拟锚固点轴力小于完全约束轴力，不满足经典解析解的基本假设．该类问题属于短管整体屈曲问题，长管的经典解析解不再适用．因此，有必要开展针对短管的解析解研究．

2) 试验研究方面

在管道整体屈曲的试验方面，由于实际工程管道发生整体屈曲波长和幅值远大于现有模型试验尺寸，因此开展大型的模型试验，使管道模型的长径比与实际工程管道相似，试验结果才能对实际工程具有指导意义．此外，积累管道工程实测数据也是管道整体屈曲研究的重要组成部分．

在管土相互作用试验方面，现有的大位移管土相互作用模型多针对轻管，因此，重管的大位移、循环加载、考虑土拱作用的管土相互作用研究有待开展．与此同时，现有的整体屈曲防护措施的研究未考虑管土间的非线性相互作用，例如枕木上管段及悬跨段管道在整体屈曲过程中所受阻力的变化，由于铺管扰动导致的土体对管道约束力的变化等．

3) 管道的水平向屈曲和轴移动耦合研究方面

对于含多个初始缺陷的管道，例如采用了蛇形铺设法、枕木法和分布浮力法等整体屈曲诱发措施的管道，在温压荷载下会发生多个整体屈曲．相邻两整体屈曲之间的虚拟锚固点会将管道分成多个含有一个独立整体屈曲的短管．已有研究表明，短管在温度梯度作用下会发生轴向移动，因此，出现水平向整体屈曲的海底管道发生轴向移动的可能性有待进一步研究．对于同时发生水平向整体屈曲和轴向移动的管道，其耦合作用机制尚不明确．

4) 整体屈曲防护研究方面

蛇形铺设法、枕木法或分布浮力法在控制管道整体屈曲的同时增加了管道轴向移动的风险．目前对管道屈曲防控措施增加管道轴向移动风险的研究尚未开展．这几种管道整体屈曲诱发方式在应用中均存在一些不足之处，例如，枕木铺设管道容易在悬跨段出现不可控整体屈曲或涡激振动，蛇形铺设法增加了管道的铺设长度且对铺管工艺施工要求高等，因此更加经济高效的管道整体屈曲防控措施研究仍在进行．