装配式框架结构的自由振动特性分析

吕田碧, 严 蔚, 李俊华, 王浩杰, 李春阳

装配式框架结构的自由振动特性分析

吕田碧, 严 蔚*, 李俊华, 王浩杰, 李春阳

（宁波大学 土木与环境工程学院, 浙江 宁波 315211）

针对装配式框架结构中梁柱节点呈半刚性的特点, 采用回传射线矩阵法研究了结构的自由振动特性. 对每个装配式框架结构中梁、柱分别采用2种不同的局部坐标系, 并考虑力的平衡条件、位移协调条件及框架边界条件, 建立了含半刚性节点的三层框架结构的回传射线矩阵方程. 采用MATLAB软件编程得到了框架结构的前18阶固有频率, 并与有限元模拟作对比分析, 验证了回传射线矩阵法在处理半刚性节点问题的有效性与正确性. 计算分析表明, 结构的固有频率对节点的半刚性特性非常敏感. 研究结果将为半刚性节点的装配式结构的动力设计提供参考.

装配式结构; 半刚性节点; 回传射线矩阵; 自由振动

近年来, 装配式混凝土结构越来越多地应用在高层建筑和大跨桥梁等重要工程中, 随之而来的就是设计上的种种难题和应用时的健康监测, 其中引起广泛关注的就是结构中梁柱之间的连接. 大量研究表明, 梁柱节点并不是传统上为简化计算而采用的刚接或铰接理想方式[1-2]. 实际工程中, 由于混凝土浇筑不均等原因造成的节点连接与原设计不符, 刚接或铰接连接方式的设计方法显然已不能满足要求. 研究还表明, 装配式混凝土节点梁柱采用半刚性节点连接, 既具有刚节点可以传递弯矩特性, 又有在梁柱之间产生一定转角的铰性优势, 这恰恰是最接近实际的节点连接方式[3-5]. 所以, 对装配式钢筋混凝土节点梁柱连接节点的正确认识, 定能为今后装配式钢筋混凝土节点的设计提供更安全可行的保障. 此外, 对于半刚性连接框架, 如果简单按照刚性框架来进行结构动力的计算, 必然会产生较大的误差, 节点柔度对结构的自振频率有很大影响. 半刚性节点刚度的降低必然将降低结构的自振频率, 特别是对结构的基本频率影响较大. 由于结构振动性能主要取决于结构的基本振型, 所以节点的半刚性程度将对结构的动力性能产生较大影响, 设计时也应考虑连接半刚性对结构动力性能的影响.

对于框架结构等此类杆系系统, 常用的动力分析方法有有限元法、传递矩阵法和回传射线矩阵法等. 其中, 回传射线矩阵法具有明确的物理意义、避免矩阵中大指数项的出现等特点, 避免了传递矩阵法中常出现数值运算困难的问题[6-7], 该方法已广泛应用于框架、桩等结构分析中. 严蔚等[8]结合压电阻抗技术对含裂缝智能梁的振动特性进行了研究, 陈进浩等[9]也采用回传射线矩阵法考察了框架结构瞬态波动响应及自振频率等, 余云燕等[10]基于回传射线矩阵法研究了成层土中部分埋入黏弹性桩顶处速度导纳及反射波.

本文采用Timoshenko梁理论来描述框架结构的振动特性, 将半刚性节点模拟成无质量但有一定刚度的转动弹簧, 利用回传射线矩阵法得到结构的固有频率, 并与有限元法模态分析得到的固有频率做对比, 来验证回传射线矩阵法应用于含半刚性节点的框架结构的可行性和有效性. 最后的计算结果将为装配式框架结构的设计尤其是动力设计提供一定的理论依据.

1 框架结构的动力分析

考察一个含半刚性节点的装配式框架结构, 如图1所示, 图中节点呈现半刚性特点,柱底部考虑固结.

主体结构控制方程为:

在简谐力作用下, 考虑稳态响应, 可假设:

由式(1)和式(2)可得:

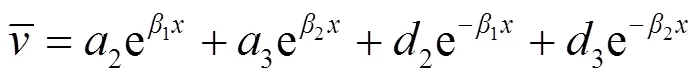
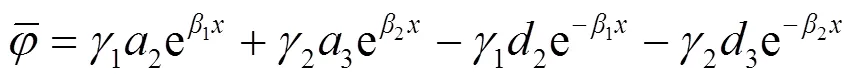
式中:

,

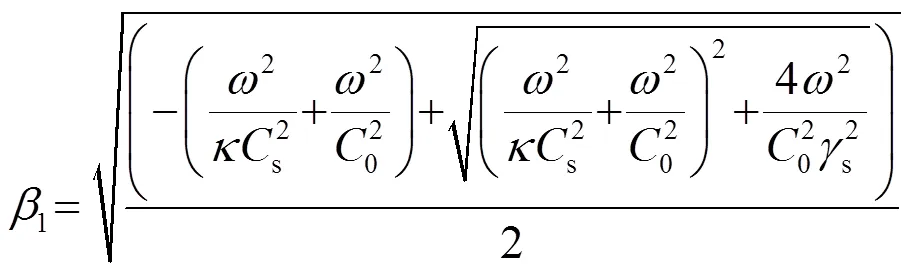
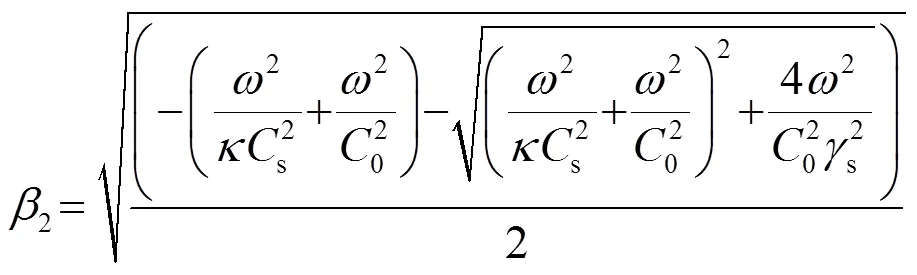
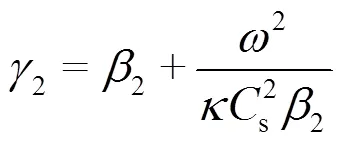
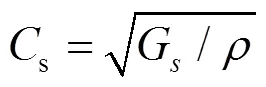
2 回传射线矩阵法求解步骤

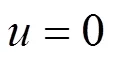
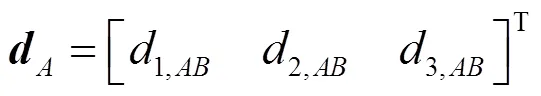
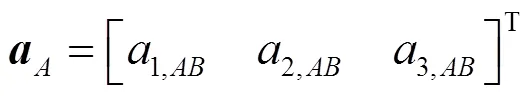
在节点, 需同时满足以下平衡条件和位移协调条件:

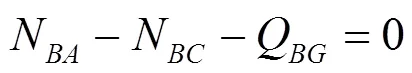
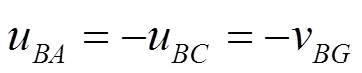
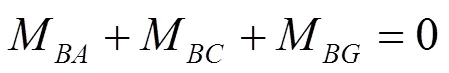
考虑到节点的半刚性特点, 有

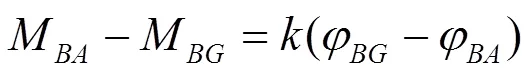
其中,是半刚性节点的刚度. 根据式(8)和式(9)可得节点的局部散射矩阵如下:

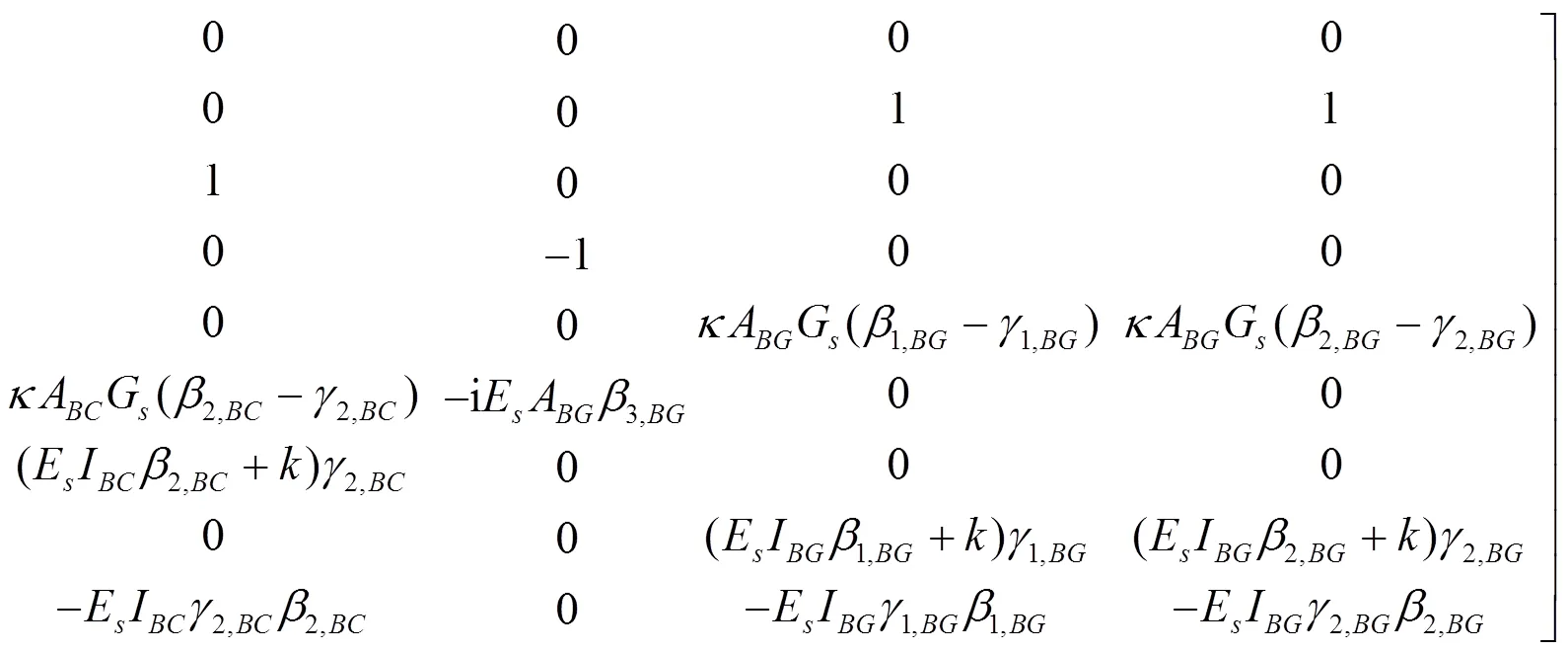
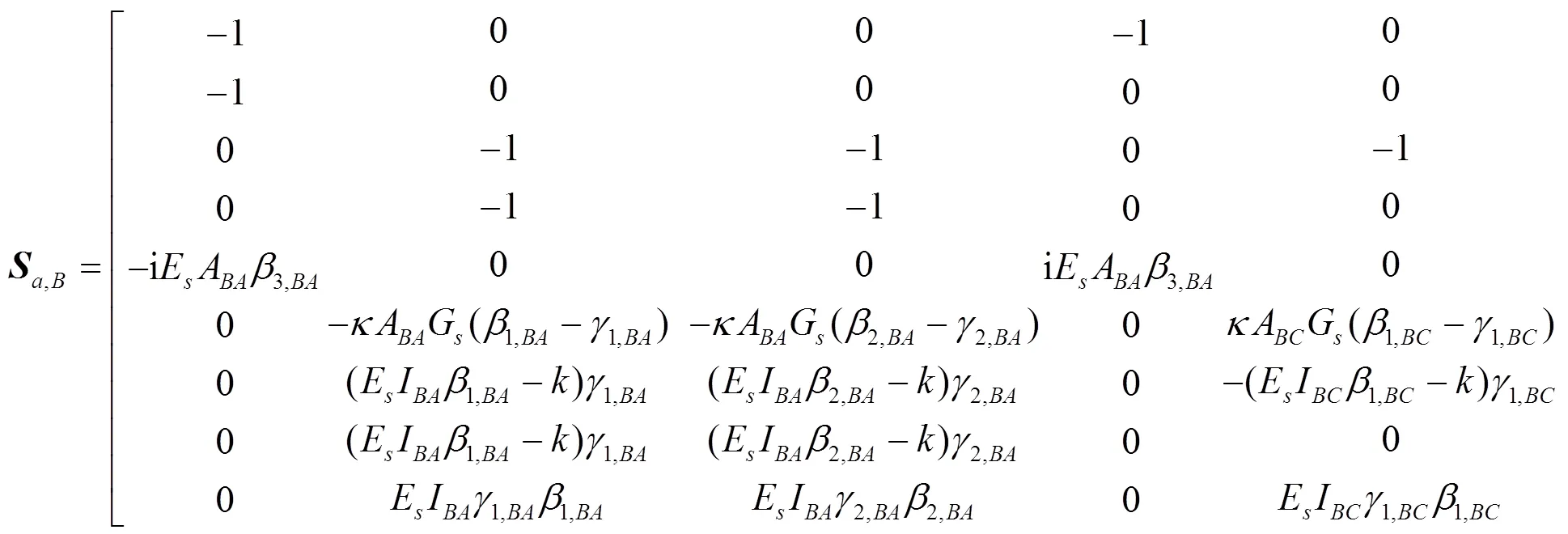
把各节点以及2个支座的所有局部散射关系结合起来, 可得整个框架结构体系的散射关系:

分别是结构整体的出射波向量和入射波向量. 整体的散射矩阵为:

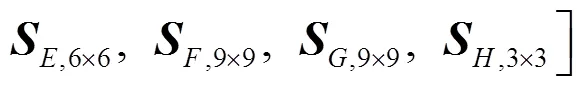
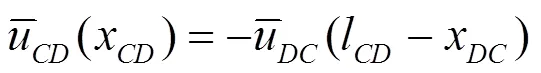
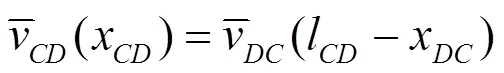
由此可得:

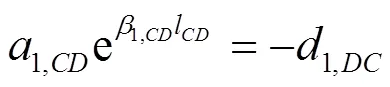
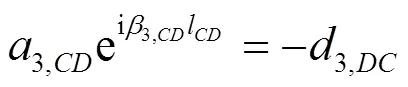
写成矩阵形式:

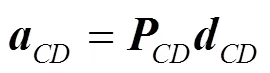
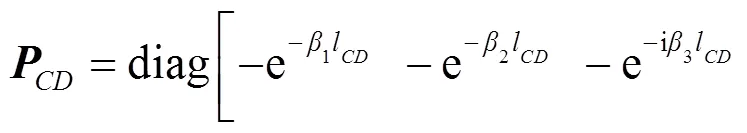
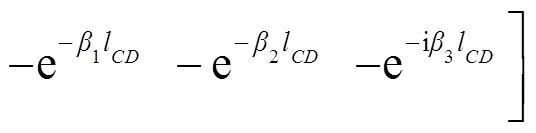
同样, 所有的梁、柱段都可类似得到相位关系. 值得注意的是, 所有相位关系的指数函数都不含有正的指数项, 这也是回传射线矩阵法能够避免数值不稳定、精准实现解析解的关键所在.

分别所有的节点及固定端中引入新的局部坐标向量如下:

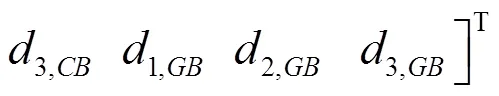
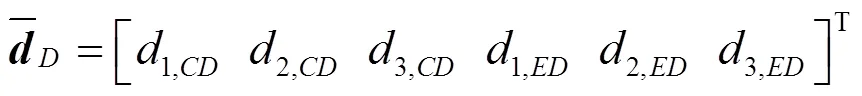
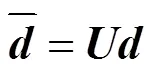
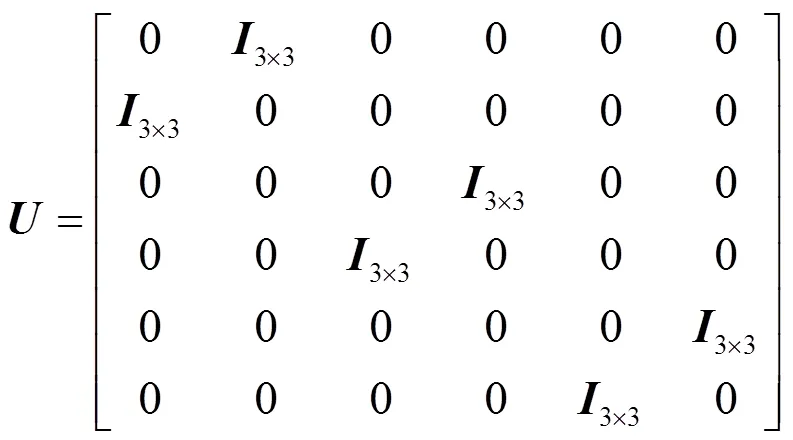
式中,为3×3的单位矩阵.

这样一来, 框架整体结构的相位关系可随之获得:

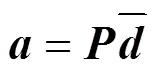
由式(12)、式(20)和式(22)联立可得:

其中,被称为回传射线矩阵;为出射波波幅向量;为入射波波幅向量; 它们是与结构振动的圆频率有关. 本文采用动力特性分析中的自由振动来求解固有特性:

3 算例分析

首先考察如图1所示三层框架结构, 梁、柱尺寸及惯性矩等数据见表1, 泊松比=0.3[11], 剪切因子取=5/6[12]. 梁长度为4m, 柱长3.6m, 其中~为半刚性节点. 选用BEAM3单元来构建装配式框架结构模型中梁柱单元, BEAM3单元是一种可承受拉、压、弯作用的单轴单元, 单元中的每个节点有3个自由度, 即沿和方向的线位移及绕轴的角位移[13-14]. COMBIN14单元用于半刚性模拟, 相当于弹簧作用在梁柱的节点处. 此单元具有一维、二维或三维应用中的轴向或扭转的性能, 轴向的弹簧-阻尼器选项是一维的拉伸或压缩单元, 它的每个节点都具有3个自由度—–,,的轴向移动.

本文中, 半刚性节点模拟的实现是定义一个固定的弹簧刚度, 在梁柱节点相同的位置定义2个不同的节点—–耦合横向和纵向位移, 最后将弹簧单元设置在相同节点处, 定义好模型后, 采用有限元模态分析功能, 来得到模型的固有频率.

有限元ANSYS模拟三层框架结构, 其中, 除底部固定节点处, 其他节点采用同个坐标的2个或3个节点, 在同个坐标的2个节点之间建立无长度的弹簧单元来实现半刚性特性.

采用回传射线矩阵法求解含半刚性节点的固有频率时, 取半刚性节点的初始转动刚度为,取5×103~1×105kN·m·rad-1[15-16], 将值代入式(10)中,即可求出点的散射矩阵, 其余节点同理可得. 改变框架中半刚性节点的刚度, 将所有公式编程输入MATLAB软件中, 采用二分法原理求行列式实部或虚部零点的求解方法[17], 分别求得各阶固有频率值(表2).

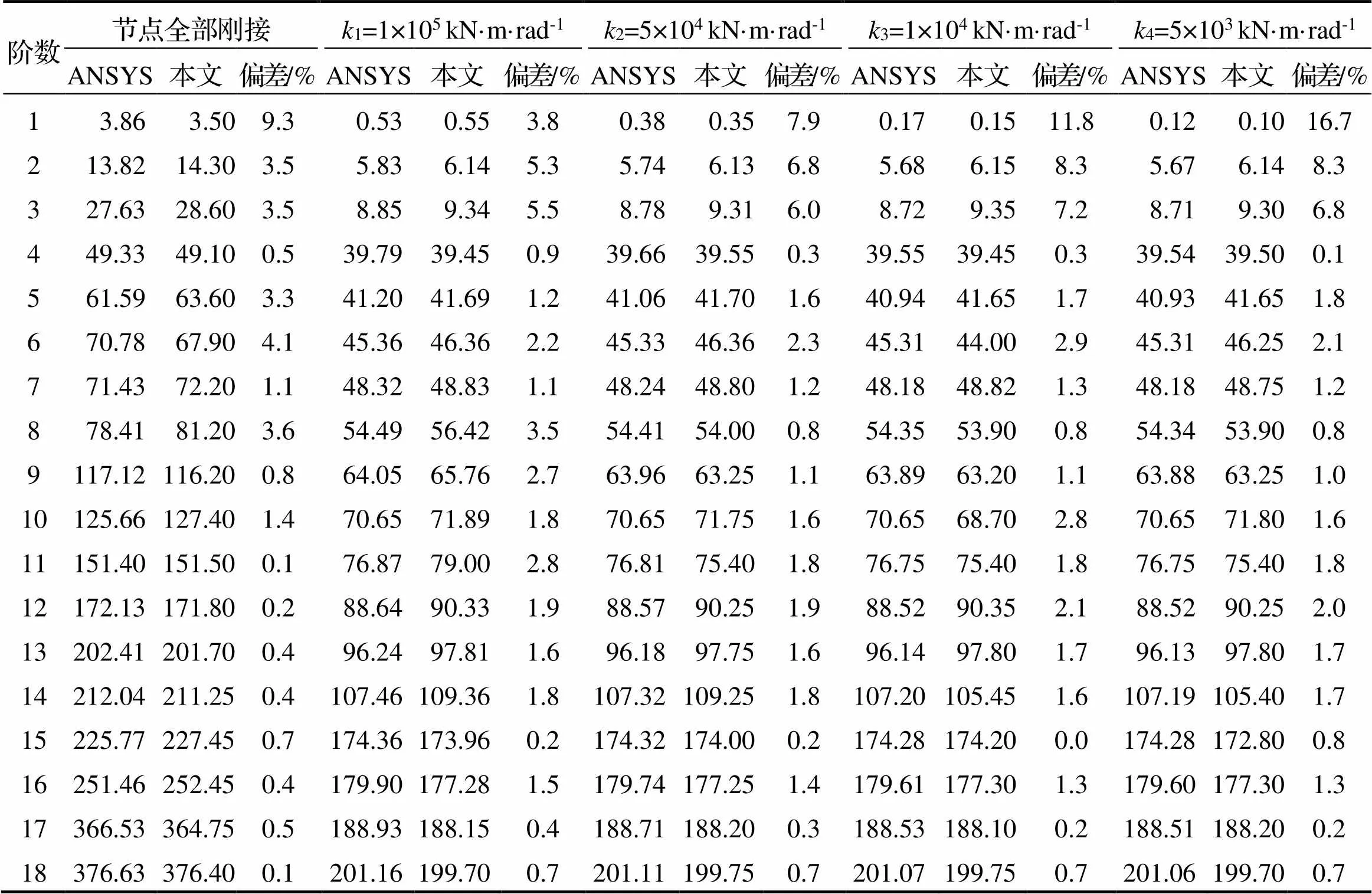
表2 三层结构不同节点刚度的固有频率数据

表3 六层结构不同节点刚度的固有频率数据

此外, 本文还进一步考察了一个六层装配式框架结构. 除底部固结外, 其余节点与装配式结构节点呈现半刚性一致, 框架结构系数参照以上三层框架数据. 求得节点半刚性不同的结构固有频率值与全部为刚性节点的自由频率见表3.

由表2和表3可见, 总体而言, 采用回传射线矩阵法得到的结构前18阶固有频率与有限元结果基本符合. 同时, 与节点刚性连接时, 比较可以发现, 由于框架节点的半刚性特点, 对应的模态频率都有明显的降低, 而且, 随着节点转动刚度的降低, 对应的固有频率也进一步降低. 表明对于装配式框架结构而言, 在结构设计中, 尤其当考虑动力因素时, 应审慎考察节点的半刚性特点.

最后, 还与框架试验测试结果作对比分析, 将文献[18]中七层节点刚性连接的钢框架试验结果与本文回传射线矩阵法得到的固有频率结果进行对比. 从表4可见, 两者结果吻合非常好, 进一步验证了本文方法的可行性和精确性.

表4 对比试验结果数据及偏差

4 结语

将回传射线矩阵法应用到含半刚性节点框架结构的动力分析中. 为了验证回传射线矩阵法对含半刚性节点的框架结构振动分析的正确性和有效性, 与有限元方法构建的含半刚性节点的框架结构模型得到的固有频率进行对比研究. 同时, 回传射线矩阵法是通过经典的Timoshenko梁理论, 经过动力学分析求解出的显式解析解, 各参数具有更明确的物理意义. 而有限元模拟的结构模型受到单元及划分网格不同等原因的影响较大.

研究结果还表明, 随着节点半刚性特性的出现, 结构的固有频率显著降低, 并且随着节点转动刚度的降低, 结构固有频率也有所降低. 所以, 在装配式结构的设计中, 尤其是动力设计中, 应该审慎考虑节点的半刚性特性. 同时, 本文编程程序的统一化也为工程实践中含半刚性节点的其他杆系结构的动力学研究提供了一种有效、便捷的计算途径. 所以, 虽然本文只研究了三层、六层的装配式框架结构, 但是该方法很容易扩展应用到更复杂, 层数更多的框架中.

[1] 吴刚, 冯德成. 装配式混凝土框架节点基本性能研究进展[J]. 建筑结构学报, 2018, 39(2):1-16.

[2] 李军军, 刘祖海, 王建国, 等. 增强门式刚架节点刚度的研究[J]. 建筑结构, 2018, 48(4):61-63; 99.

[3] 何嘉年, 王湛. 半刚性连接钢框架结构体系优化设计[J]. 土木工程学报, 2015, 48(增1):98-103.

[4] 布欣, 谷倩, 王新武. 剖分T型钢梁柱连接框架中柱空间节点抗震试验研究[J]. 工程力学, 2017, 34(8):105- 116.

[5] 石永久, 王萌, 王元清, 等. 钢框架端板连接半刚性节点受力性能分析[J]. 工程力学, 2011, 28(9):51-58.

[6] Yan W, Chen W Q. Dynamic analysis of semi-rigidly connected and partially embedded piles via the method of reverberation-ray matrix[J]. Structural Engineering & Mechanics, 2012, 42(2):269-289.

[7] Tang D, Yao X, Wu G, et al. Free and forced vibration analysis of multi-stepped circular cylindrical shells with arbitrary boundary conditions by the method of reverberation-ray matrix[J]. Thin-Walled Structures, 2017, 116:154-168.

[8] 严蔚, 袁丽莉. 基于回传射线矩阵法的含裂缝智能梁的动态特性[J]. 振动与冲击, 2010, 29(6):101-104; 239.

[9] 陈进浩, 余云燕. 框架结构瞬态波动响应及自振频率的回传射线矩阵法分析[J]. 振动与冲击, 2016, 35(10): 83-90.

[10] 余云燕, 姚栋. 基于回传射线矩阵法成层土中部分埋入黏弹性桩的波动响应研究[J]. 振动与冲击, 2015, 34 (14):56-64.

[11] 陈家梁. 装配式钢板笼混凝土框架结构整体抗震性能研究[D]. 合肥: 安徽建筑大学, 2016.

[12] 葛仁余, 张金轮, 姜忠宇, 等. 轴向功能梯度变截面Timoshenko梁自由振动的研究[J]. 振动与冲击, 2017, 36(22):158-165.

[13] 时庆伟. 门式刚架轻型钢结构优化设计研究[D]. 沈阳: 沈阳建筑大学, 2011.

[14] 职君静, 严蔚, 雷庭杰, 等. 长期荷载作用下含粘弹性界面层合板的力学行为[J]. 宁波大学学报(理工版), 2017, 30(1):77-81.

[15] 王可峰, 李慧. 半刚接钢框架柱稳定承载力研究[J]. 钢结构, 2018, 33(2):19-25.

[16] 张一舟, 王元清, 施刚, 等. 节点刚度对多层平面钢框架抗震性能的影响分析[J]. 土木工程与管理学报, 2006, 23(2):41-45.

[17] 郭永强, 陈伟球, 肖春文. 复杂空间框架结构的自振特性分析[J]. 振动工程学报, 2008, 21(3):261-267.

[18] Li J, Hao H. Substructure damage identification based on wavelet-domain response reconstruction[J]. Structural Health Monitoring, 2014, 13(4):389-405.

Free vibration analysis of prefabricated frame structures with semi-rigid joints

LÜ Tianbi, YAN Wei*, LI Junhua, WANG Haojie, LI Chunyang

( School of Civil and Environmental Engineering, Ningbo University, Ningbo 315211, China )

Due to the semi-rigid properties of beam-column joints, a method of reverberation-ray matrix is employed to investigate the free vibration of the prefabricated frame structures. Two different local coordinate systems are used for the beams and columns in the prefabricated frame structure. Considering the conditions of the force balance, the coordination conditions of the displacement and the boundary conditions of the frame, the reverberation-ray matrix formulations are established for a three-storey prefabricated frame structure with semi-rigid joints. The first 18-order natural frequencies of the frame structure are calculated in MATLAB. The results are compared with those from finite element simulation, which verifies the effectiveness and correctness of the present method in dealing with the dynamics of a framed structure with semi-rigid nodes. The numerical analysis shows that the natural frequencies are very sensitive to the semi-rigid properties of the prefabricated frame structures. Furthermore, the results of this study will provide theoretical ground for the future dynamical design of the prefabricated structures.

prefabricated structure; semi-rigid joins; reverberation-ray matrix; free vibration

TU323.5

A

1001-5132（2020）01-0088-07

2018−12−18.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家重点研发计划项目（2016YFC0701804）; 宁波市自然科学基金（2017A610315, 2018A610353）.

吕田碧（1992－）, 女, 河北廊坊人, 在读硕士研究生, 主要研究方向: 防灾减灾及防护工程. E-mail: 1050392916@qq.com

严蔚（1968－）, 男, 浙江宁波人, 博士/教授, 主要研究方向: 智能材料与结构力学. E-mail: yanwei@nbu.edu.cn

（责任编辑 章践立）