基于动态主元分析和极限学习机的分解炉出口温度预测
2020-01-08
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
水泥工业是我国国民经济建设的重要基础材料产业,也是高能源消耗和高污染排放的行业之一[1],所以节能环保的生产方式尤为重要。预分解是新干法水泥生产技术的核心步骤[2],而分解炉出口温度是反映分解炉运行工况优劣的关键指标,对水泥生产的质量、产量及能耗起着至关重要的作用,所以对分解炉出口温度的研究具有重要意义[3]。近年来,许多学者围绕分解炉温度的预测和控制展开研究。文献[4]提出基于遗传算法优化的BP网络出口温度预测模型,并进行了仿真验证;文献[5]在极限学习机与回归分析的基础上,建立了出口温度的T-S模糊模型;文献[6]和文献[7]分别运用神经网络与自适应PID的方法,实现了对分解炉温度的控制;文献[8]提出一种基于参数优化的支持向量回归的方法预测分解炉温度,取得了预期的预测效果。但是上述研究在关于影响分解炉温度的变量选择上,大都是采用传统的经验法,以风(三级风)、料(生料量)、煤(喂煤量)等主要变量对分解炉系统进行研究。由于分解炉内部结构复杂、变量众多、理化反应交织,人为经验法选取的少数变量难以全面概括分解炉系统的内部规律,易造成预测精度不高,模型的泛化能力较弱等问题。而将多元统计分析方法与神经网络算法相结合的数据驱动建模方法,由于包含可能影响系统的全部变量,又具有神经网络强大的计算拟合能力,所以能够更为科学准确地把握系统特性,因此更适用于多变量、非线性和不确定性的分解炉出口温度建模预测。
本文提出基于动态主元分析(Dynamic Principal Component Analysis,DPCA)与极限学习机(Extreme Learning Machine,ELM)相结合的DPCA-ELM预测模型对分解炉出口温度进行预测。利用DPCA消除变量之间的相关性,计算出各输入变量在不同时序下对输出的影响,降低数据的冗余和噪声,减少ELM的输入维度。然后将降维所得的主元作为极限学习机的输入层,再通过PSO粒子群寻优算法求得ELM网络的最优权值和偏置,再由方程组计算确定隐含层至输出层的权值,经训练、调参,从而完成对出口温度的建模预测。经仿真验证表明,基于DPCA-ELM的分解炉出口温度预测模型具有良好的预测精度,同时也为其他复杂、非线性、多变量工业系统建模提供参考。
1 理论分析
1.1 主元分析法与动态主元分析法
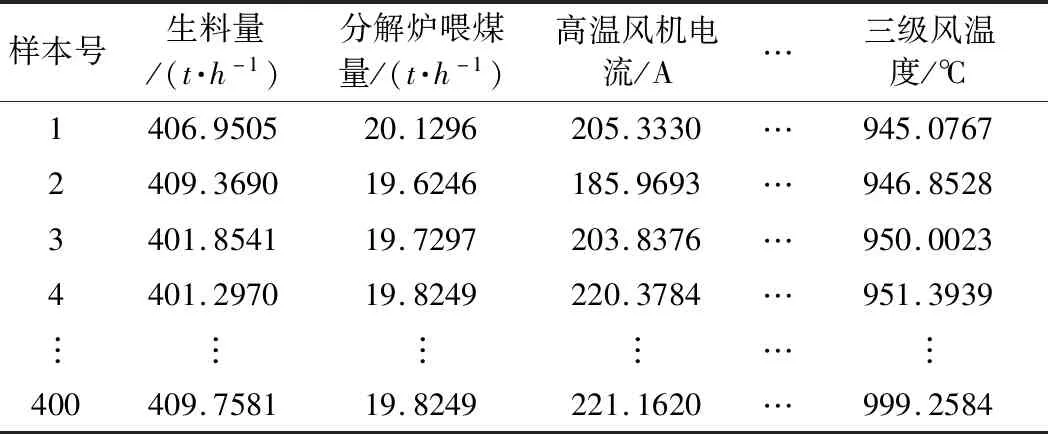
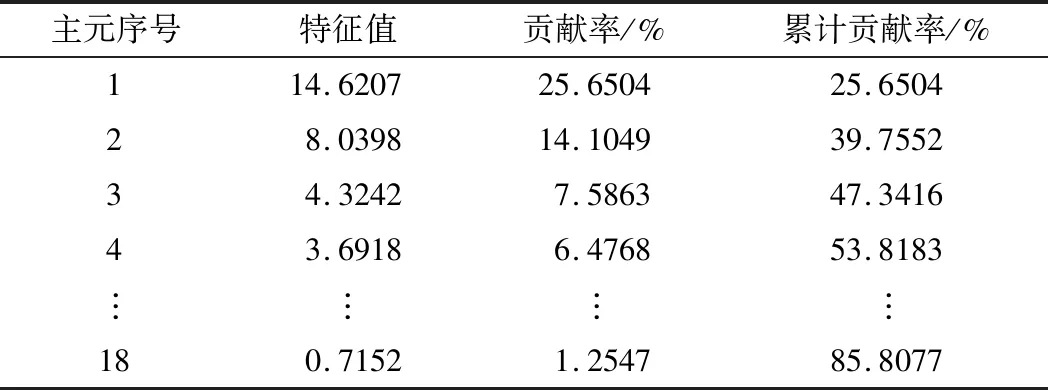
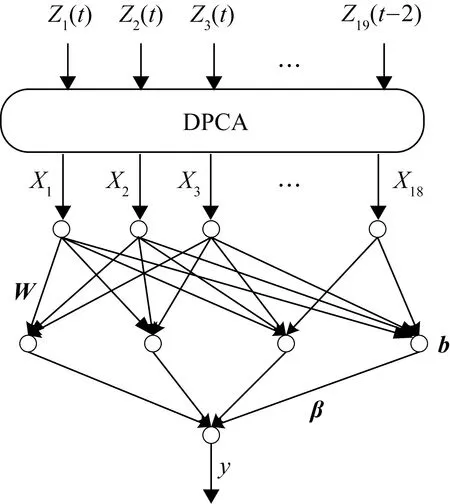
主元分析(PCA)的基本原理就是将多维的线性相关的原始数据Xn×m转化为低维且线性无关的新数据Tn×k,其中k (1) X的标准化S又可以表示为得分矩阵和相关系数矩阵的外积形式: S=Tn×mRm×m (2) 式中,矩阵R=(r1,r2,…,rm)为S的相关系数矩阵;T=(t1,t2,…,tm)为S的得分矩阵。若‖t1‖>‖t2‖>…>‖tm‖,则t1即为第一主元,代表X在其对应方向的投影最大。 取前k个主元,可得S=TkRk+E,式中E为残差矩阵,主元Tn×k=(t1,t2,…,tk)即为降维后的新数据。 虽然传统的PCA算法可以降低变量维度,减少数据冗余,但是对于有时序的系统模型,传统的PCA会忽略某些变量对模型输出的动态影响,从而影响模型的可靠性,而DPCA可以通过添加前h时刻的增广矩阵弥补传统PCA的静态不足的问题。增广矩阵为 (3) 式中,x为t时刻在训练集中的m维观测向量对于滞后因子h的确定,由递推公式(4)递推至rn(h)>0: (4) 经计算当h=2时,rn(h)>0,故确定滞后因子为2。 极限学习机算法是由新加坡学者黄广斌等人在2004年提出的一种单隐含层前馈神经网络学习算法,具有预测精度高,训练速度快等优点。 对于单隐含层神经网络,设有n组多变量输入样本Xi=[xi1,xi2,…,xin]T∈Rn,多变量输出样本Ti=[ti1,ti2,…,tim]T∈Rm。则网络的输出可以表示为 (5) 式中,j=1,2,…,n;L为隐含层节点数;βi为输出权值;f(x)为网络的激活函数;Wi=[wi,1,wi,2,…,wi,n]T为输入层到隐含层权值;Xj为网络输入;bi为第i个隐含层节点的偏置。网络学习的目的是实际输出Oj与目标的误差尽可能的逼近于0,可以表示为 (6) 等价于存在βi,Wi和bi,使得式(7)成立。 (7) 式(7)又可以等价表示为Hβ=T,其中,H是隐含层节点的输出,β为输出层的权值,T为网络期望输出。式中,β、T、H可以表示为[12] (8) (9) (10) 式中,i=1,2,…,L,求解式(10)等价于求解损失函数的最小值: (11) (12) 水泥分解炉作为新干法水泥生产的核心部分,承担了燃烧加热、气固换热、物料反应与分解等多个步骤。因此机理建模预测在水泥分解炉系统中的建立显得尤为困难。故本文采用数据驱动建模的方法,建立了基于水泥生产过程中所采集的生产数据的DPCA-ELM分解炉出口温度预测模型,并在Matlab环境下,完成仿真验证。 本文数据来自2014年6月,某水泥公司6000 t/d水泥生产线的现场数据,采集数据的时间间隔为1 min。从稳定工况下选取400组作为训练样本,再选取100组测试样本用来测试模型的有效性。水泥分解炉的系统结构复杂,其内部理化反应众多,故本文参考水泥生产实际过程和文献确定与模型输出相关的输入变量,其中包括:生料量、喂煤量、三级风风温和风压、各级旋风筒出口温度以及气压、高温风机电流、转速等。训练样本原始数据见表1。 表1 训练集样本原始数据 选取如上输入变量中生料量、喂煤量等19个变量,经计算滞后因子h=2,故添加前两个时刻的数据构成主元分析的增广矩阵,再采用DPCA算法对输入变量进行降维,以简化ELM网络输入单元个数。 在进行主元分析前,首先要判断各变量之间是否存在相关性,以检验主元分析的适用与否。所以本文采用KMO统计检验方法,KMO的值δ越接近1,数据越适宜采用主元分析。其检验公式如下: (13) 式中,rij为所有变量的简单相关系数;aij为所有变量的偏相关系数。经检验计算,筛选后变量的KMO值δ=0.9518,故筛选后的变量非常适宜使用主元分析进行降维。 将筛选后的数据标准化,消除因量纲不同所产生的不利影响。再求出相关系数阵的特征值λ1,λ2,…,λi,…,λ57,及其对应的特征向量p1,p2,…,pi,…,p57,并将特征向量按其对应特征值由大到小排列。计算特征值累积贡献率(Cumulative Percent Variance,CPV)其公式为 (14) 式中,分母为所有特征值的累加值;分子为主元的累加值。设定CPV的期望值为85%,经计算得k为18时,CPV的值达到85.8077%,故取主元个数为18,其特征值及主元贡献率见表2。 表2 特征值及主元贡献率 最后由原始数据X和主元的特征向量的乘积求得降维后的主元Tn×k=(t1,t2,…,ti,…,t43),式中,ti=Xpi。 将主元作为极限学习机网络的输入层,即网络有18个输入节点。选取激活函数为sigmoid函数,其表达式为 (15) 选取性能函数为均方误差MSE(Mean Squared Error)与拟合优度R2(R-square),其表达式为 (16) (17) 在ELM中,输入权值与隐含层偏置随机产生,无需迭代,输出权值由式(12)确定。但由此产生的参数随机性较大,且所需隐含层节点数过多,易导致模型复杂度加大,泛化能力下降。故本文采用粒子群寻优算法(PSO)代替ELM权值偏置随机产生。 PSO优化算法的参数设置参考文献[14]所述,并验证其在本模型的可行性。其具体设置为:粒子数30;最大和最小惯性权重分别为0.9和0.4;学习因子c1,c2同为1.4961;最大迭代次数为80次;激活函数为sigmoid函数;适应度函数为MSE。 PSO算法适应度随迭代次数变化曲线如图1所示,当迭代次数在70次左右时,适应度值稳定在0.0373不再变化,训练收敛,权值和偏置寻优过程结束。 图1 适应度随迭代次数变化曲线 对于ELM隐含层节点个数的确定,参考文献[15],设定初始隐含层节点数为20,再以5为增幅进行训练预测,每个节点重复预测20次,并对所得性能指标取平均值。不同隐含层节点个数预测的平均性能指标如表3所示。 表3 不同隐含层节点个数性能指标 由表3看出,随着隐含层节点个数的增加,训练样本预测效果越好,测试样本预测效果在节点数为80时预测效果最佳,当隐含层节点个数由80继续增加时,测试样本预测效果变差。其性能函数随节点数变化趋势如图2所示。 图2 预测效果随节点个数变化趋势 由图2可以看出,在节点个数为80时,测试集MSE最小,拟合优度R2最大,对测试样本数据的预测结果最佳。故确定隐含层节点数为80时,模型预测与泛化能力最佳,其训练时间为50.8255 s。出口温度预测模型如图3所示。 图3 DPCA-ELM预测模型 其中,Zi为时滞h为2的原始变量,Xi为动态主元分析降维所得的18个主元,即ELM的输入层,W为输入层权值,bi为第i个隐含层节点的偏置,βi为第i个隐含层节点的输出权值,y为输出的预测出口温度。 将选取的100组测试集样本变量数据导入DPCA-ELM预测模型,100组测试集样本如表4所示。 表4 测试集样本原始数据 经DPCA-ELM模型预测后,得到测试集预测输出。100组出口温度预测结果与实际数据对比及误差如表5所示。由表5可以看出测试集预测效果良好且稳定。 经计算,DPCA-ELM模型预测的最大误差约为5.1294 ℃,平均预测误差约为1.2013 ℃,相对误差平均值约为0.1285%。 表5 测试样本预测结果与误差 为了进一步验证DPCA-ELM模型的有效性与优势,将其与文献[4]所提出的GA-BP模型的预测效果进行对比。 设置遗传算法参数:进化代数:100;种群规模:50;交叉概率:0.7;变异概率:0.1。 重复试验观察后,设置BP神经网络的隐含层数为45;激活函数设置为动量梯度下降法(Gradient Descent with Momentum)函数traingdm;迭代次数为200;学习步长为0.01;性能函数为MSE;目标值为0.001。 GA-BP模型的训练时间为21.7242 s。经训练后,建立了遗传算法优化的BP网络的出口温度预测模型,将测试样本数据导入模型,得到测试样本预测输出。DPCA-ELM模型和GA-BP模型预测结果与测试样本实际对比如图4所示。 由图4可以看出,基于DPCA-ELM模型的出口温度预测效果良好,GA-BP模型预测效果稍差。其预测结果与误差对比如表6所示。 由表6可以得出:基于DPCA-ELM的出口温度预测模型具有精度高、拟合度好、训练速度快等优势。基于GA-BP网络的预测模型,由于输入维度高,遗传算法编码复杂,所需迭代参数较多,故训练速度较慢,泛化能力较弱,影响对出口温度预测的精度。 图4 测试样本预测效果对比 模型MSER2EmaxEmeanGA-BP10.57910.63257.08122.8773DPCA-ELM2.36750.91315.12941.2013 本文提出了一种数据驱动建模方法:首先进行KMO统计检验,验证PCA的适用性,然后计算出滞后因子,使用DPCA降低影响分解炉出口温度变量的维度,消除变量之间的相关性。在此基础上,构建以低维数据为输入层的ELM预测模型,再使用PSO算法优化参数,通过训练、调参,最终求得最优DPCA-ELM出口温度预测模型,并使用该模型对测试样本进行预测。最后通过与GA-BP神经网络预测模型的对比分析,体现DPCA-ELM预测模型良好的预测精度和泛化能力。1.2 极限学习机


2 出口温度建模预测
2.1 数据来源与变量筛选
2.2 KMO检验与PCA降维
2.3 DPCA-ELM预测模型参数设置与训练




3 仿真验证
3.1 测试数据及预测


3.2 预测结果对比分析


4 结束语
