考虑应力状态对土体力学参数影响的边坡稳定性分析方法

2020-01-08邓海峰

水利与建筑工程学报 2019年6期

邓海峰，祁磊，许浩，李春

(1.中国石油集团工程技术研究有限公司, 天津塘沽 300451;2.中国石油集团海洋工程重点实验室，天津塘沽 300451)

边坡稳定性分析首先需要确定边坡的滑移机制，而边坡内部应力状态及土体强度是确定滑移机制的重要因素[1-3]。

传统的边坡稳定性分析大都采用极限平衡法-条分法进行计算，在对坡体进行安全性评价过程中，忽略了坡体的应力状态及其变化过程及其对土体力学参数的影响程度。目前，多采用条分法对边坡稳定性进行分析，方法中包含了多种基本假定，且关键问题是正确寻找滑动中心和滑裂面位置和形状。但由于这种方法固有的缺陷及存在的静不定问题，同时并没有考虑土体应力状态变化对安全度的影响[4-6]，使该方法在实际工程应用中面临着巨大挑战。因此应当建立土坡与其应力状态及其变化相适应的评价方法。

本文以土体的应力状态为主线，基于室内空心扭剪试验量化了主应力方向与土体强度参数的关系，并结合作图法推导出均质土坡圆弧平面滑动的稳定安全系数计算公式，与传统计算方法对比结果说明，这种方法具有理论背景概念明确，依据清晰等特点，可弥补传统计算方法的不足，结果更接近实际。

1 主应力方向与强度参数的量化关系

1.1 试验设备

试验仪器为美国GCTS空心圆柱扭剪仪HCA-100。设备可对空心试样施加独立控制的外压p0，内压pi，轴力W和扭矩Mt(见图1)，从而在图2所示的试样环状薄壁单元体上实现大小主应力垂直于试样径向(不变的中主应力方向)的切平面中旋转的复杂应力路径。加载参数与应力参数之间的映射关系采用有关文献结果[7-8]。

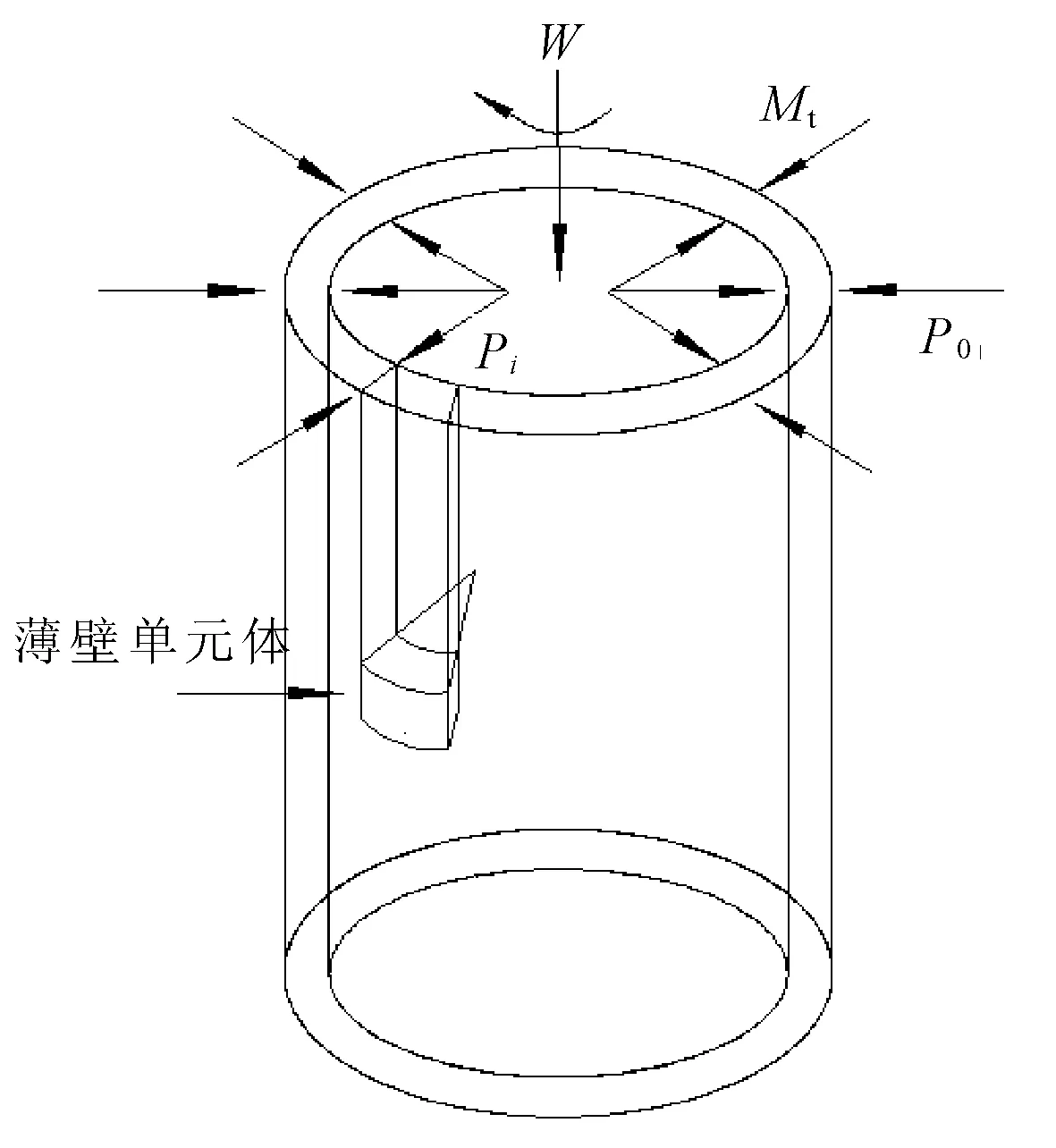
图1 空心圆柱试样受力示意图

设备的加载控制系统中具备相关控制模块，可直接将荷载换算成应力施加在试样上，具体方式可参见图1和图2。并可以根据试样实时变形测量结果，对应力进行实时修正。在所有参数中，α为偏离轴向的大主应力方向角，其他三参数的定义如下：

b=(σ2-σ3)/(σ1-σ3)

(1)

p=(σ1+σ2+σ3)/3

(2)

q=σ1-σ3

(3)

此应力控制方案为研究平均主应力和主应力方向固定不变剪切对土体强度参数的影响提供了重要途径。

图2 空心圆柱试样薄壁单元体受力状态

1.2 试验土样基本性状

本文中所取土样源于安徽某基坑工程的原状黏土，实际工程问题为放坡开挖基坑，使基坑达到稳定安全标准。基坑开挖深度9.54 m，坡度系数为3，确定坡体稳定安全系数，基坑开挖深度内为均质黏性土。

在该层钻孔取样获取15组原状土样，土体比重Gs=2.72～2.75，孔隙比e=1.02～1.124，含水率w=19.6%～26.6%，湿密度ρ=1.64 g/cm3～1.75 g/cm3，饱和度50.3%～65.1%，塑限wp=16.7%～18.3%，液限wL=37.5%～45.0%，OCR=0.94～1.59，属于正常固结土。

试样尺寸为200(H)×100(D0)×60(Di)，单位mm。综合利用常规切土工具和GCTS专用削土器，分别制备多组实心圆柱试样和空心圆柱试样。

1.3 试验加载方案

将试样在三轴压力室中首先进行反压饱和，然后对试样施加各向同性固结压力进行初始固结，确保各向有效压力相同。按照《土工试验规程》[9](SL 237—1999)，将1 h内排水量小于0.1 mL作为固结稳定标准。待固结完成后，进行主应力方向固定不变的剪切试验。

根据《建筑边坡工程技术规范》[10](GB 50330—2013)，在土质边坡整体稳定性计算中，对黏性土宜选择直剪固结快剪或三轴固结不排水剪。此处选择三轴固结不排水剪强度指标。

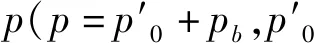
该方案主要考虑滑动面不同位置处大主应力方向不同，且与沉积方向也存在明显差异的均质滑坡，而常规三轴试验获得的土体强度无法反映原状土的各向异性特征。该方法致力于量化主应力方向与土体强度间的关系，为边坡稳定性计算提供真实合理的力学参数。

空心扭剪试验应力路径如图3所示，即先施加固结应力p，一段时间后，施加q值进行定向剪切。

表1 主应力方向固定不变的剪切试验方案

图3 空心扭剪试验应力路径

1.4 试验结果分析

根据摩尔-库仑破坏理论可知：

(4)

结合试验结果和摩尔-库仑公式，分析得到不同主应力方向角与土体强度参数之间的量化关系，如图5所示。

图4 不同主应力方向及不同围压下所得归一化抗剪强度

图5 主应力方向与土体强度参数之间的量化关系

以α=45°为分界点，分段拟合得到不同主应力方向条件下的c和φ值：

当α<45°时，

φ=-0.182α+18.182
c=-0.386α+34.22

(5)

当α>45°时，

φ=0.068α+6.765
c=0.114α+12.72

(6)

边坡圆弧滑裂面不同位置的主应力方向和大小均不相同，且差异显著，最终表现为土体强度参数的不同，即抗剪强度不同，以用于推导得到边坡稳定性分析方法。

2 边坡稳定性分析

2.1 边坡滑动面确定

边坡滑动面的确定方法通常采用作图法、对数螺旋线法和自动搜索法。其中作图法考虑了主应力方向与破坏之间的关系，与本文的研究前提一致，因此采用这种方法确定边坡滑动面。

作图法理论依据：(1) 针对均质边坡，破坏面一般通过坡脚；(2) 坡面处土体处于单向应力状态，大主应力方向与坡面平行；(3) 坡内连续土体单元所受剪应力达到抗剪强度时，即形成整体滑裂面，如图6所示。

图6 破坏面与坡面的关系

破坏面与大主应力作用方向即坡面夹角为：

θ=45°-φ/2

(7)

确定滑动面的具体做法参见文献[12]，潜在滑动面如图7所示。根据作图法原理及其结果可知，整个边坡滑动面为一圆弧，如图7所示。因此可以采用以坡脚为笛卡尔坐标系为原点，水平和竖直方向分别为x、z轴的圆弧轨迹方程表示。

图7 作图法确定潜在滑动面媚

(8)

也可表述为z=z(x)。

其中，(a,b)为滑动圆弧圆心坐标，可通过作图法计算得到。

2.2 边坡稳定性计算方法

定义边坡稳定安全系数Fs等于土体总抗力与根据应力状态计算得到的最大剪切内力之和的比值(参见文献[13])，用式(9)表示：

(9)

研究思路：根据作图法确定滑动面位置及形状，建立坐标系(以坡脚为坐标原点建立笛卡尔坐标系)，将滑坡面采用z=z(x)数学表达式进行表示；基于滑动面方程计算得到滑动面任意位置处的切线倾角，根据土体破坏机理(大主应力σ1作用方向与破坏面呈45°-φ/2)确定大主应力σ1的作用方向，参见公式(19)；按照公式(10)[14]计算滑动面任一位置处的水平应力σx；再根据莫尔应力圆计算得到应力圆的位置和大小，包括剪应力大小；最后根据公式(9)计算安全系数。详见图8。

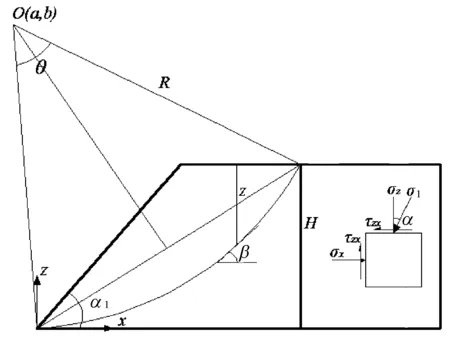
图8 边坡稳定性计算原理图

(10)

其中:R为滑动面半径;θ为滑动面弧度;α为主应力方向与竖直方向的夹角;H为边坡高度;α1为边坡坡脚;β为条块底面中点切线与水平面的夹角;z为自由表面至条块底面中点的距离;i为第i个条块。

根据公式(9)可知，计算边坡稳定安全系数，需得到抗剪强度τf和内部剪切应力τmax，计算公式分别如下所示：

τf=c+σtanφ

(11)

σ=(σ1+σ3)/2

(12)

τmax=(σ1-σ3)/2=(σz-σx)/(2cos(2α))=

(γz-γztan2(π/4+φ(α)/2)-2c(α)tan(π/4+φ(α)/2))/(2cos(2α))

(13)

其中：

(14)

(15)

式中:c和φ均为主应力角α的函数，分别表示为c(α)和φ(α)，设滑动面为x的函数，表示为z=f(x)。

(16)

σz=γz

(17)

β=z′(x) ；

(18)

α=45°+φ/2-β(假设当α<0时，取值α=0)

(19)

τf=c+σtanφ=c+(σ1+σ3)tanφ/2=c(α)+(σ1+σ3)tanφ(α)/2=c(α)+(σx+σz)tanφ(α)/2=c(α)+(γztan2(π/4+φ(α)/2)+2c(α)tan(π/4+φ(α)/2)+γz)tanφ(α)/2

(20)

(21)

3 算例分析

算例尺寸及土体参数详见第1.2和1.4节。

对比分析该基坑放坡开挖后的边坡稳定性，分别采用瑞典条分法和本文的计算公式进行计算。

其中采用瑞典条分法时，土体参数采用主应力方向为0°的三轴压缩试验抗剪强度指标，即常规三轴压缩试验，而采用本文的计算方法中，引入了强度参数和主应力方向角之间的量化关系。对比分析结果如表2所示。

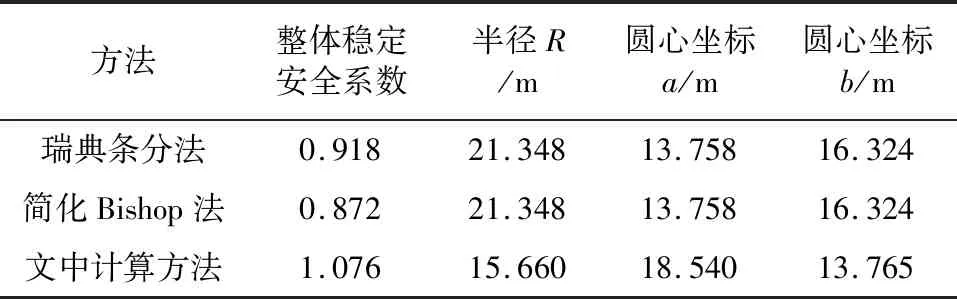
表2 边坡稳定安全系数对比结果

根据表2计算结果可知，本文计算得到的稳定安全系数高出17%。与瑞典条分法相比，简化Bishop法[15]进一步低估了约5%。众所周知，瑞典条分法忽略了土条两侧条间力对破坏面上法向作用力Ni的影响，假定条间力合力大小相等，方向相反，相互抵消，导致安全系数偏低5%～20%。本文的计算方法虽然考虑了主应力轴方向对土体的强度参数的削减作用，但该方法的理论背景概念明确，依据清晰，同时结合了具有明确力学破坏概念的作图法所得到的破坏面，因此计算结果较接近真实结果。