扁平率对浅埋大跨度隧道围岩稳定性的影响

王 昆， 王育平

(山东科技大学 矿业与安全工程学院， 山东 青岛 266590)

随着城市化进程的加快，地铁等地下交通隧道数目在逐年增加的同时，隧道的跨度也在逐渐增大，大跨度和超大跨度隧道越来越多[1]。在实际工程中，通常把隧道断面设计为椭圆形，这一形状既可以满足多车道通行的需求，又可以提高隧道断面利用率，降低建设成本。扁平率是指隧道高度一半与隧道跨度一半的比值。近年来，我国学者就大跨度隧道扁平率的问题进行了相关研究。吴绍升[2]、胡云鹏[3]和朱苦竹[4]等针对不同施工方法进行了相应的研究。李世麟[5]、朱彦鹏[6]和卿伟宸[7]等对大跨度隧道的支护结构进行了受力分析，明确了支护结构的受力特点。雷建海[8]、金星亮[9]和王建[10]等通过对支护结构和围岩的受力分析，确定了研究工况下的最优扁平率。武明静[11]和陈卫忠[12]等基于层次分析法对隧道的扁平率进行了优化。吕爱钟[13]和Ren[14]等基于隧道围岩的应力分布状态提出了洞形优化方法。范君黎等[15]通过扩展有限元法和模型试验的方法研究了不同扁平率下裂纹扩展规律。

但是，目前的研究主要集中在隧道径向二维平面内，对隧道纵向平面的研究少之又少。同时，对隧道径向平面的研究仅仅研究了距掌子面较远处平面应变条件下的影响规律，并不能显示掌子面附近的变化特点。因此，明确扁平率对隧道纵向位移的影响具有十分重要的意义。本论文结合青岛某区段具体的工程背景，借助FLAC3d软件进行数值模拟，对浅埋大跨度花岗岩隧道开挖引起的围岩稳定性问题进行研究。

1 数值模型

研究区域隧道埋深16～18 m，上部为1～2 m的杂填土，下部是花岗岩。花岗岩地层根据岩石的风化程度和破碎程度的不同，主要分为3层，围岩级别主要为Ⅱ～Ⅲ级，部分为Ⅳ～Ⅴ级。地层从上往下依次为杂填土、花岗岩岩层1、花岗岩岩层2和花岗岩岩层3，该段隧道在花岗岩岩层3中开挖。表1为该标段的地层参数。

表1 地层参数

为消除边界对模拟结果的影响，根据隧道开挖的影响范围，参考已有的计算经验，取模型左右边界为隧道外径的3倍，模型底部取隧道外径的1.5倍[16]。这里的隧道外径即为扁平率为1时的隧道半径。本构模型选用摩尔-库伦模型。采用更改强度参数弹塑性求解的方法生成初始地应力[17]。为研究扁平率对隧道应力和位移的影响，文中扁平率取0.55，0.70，0.85，1.00等4个水平，隧道跨度取18，20，22 m等3个水平。

2 地表沉降与隧道变形

2.1 地表沉降

隧道开挖不可避免的会引起地层移动，降低隧道开挖引起的地表沉降是地层变形控制的最终目标之一。图1是不同跨度下扁平率对地表沉降的影响曲面图。在图1三维沉降图中，变形曲面自下而上的扁平率依次为0.55，0.70，0.85，1.00。

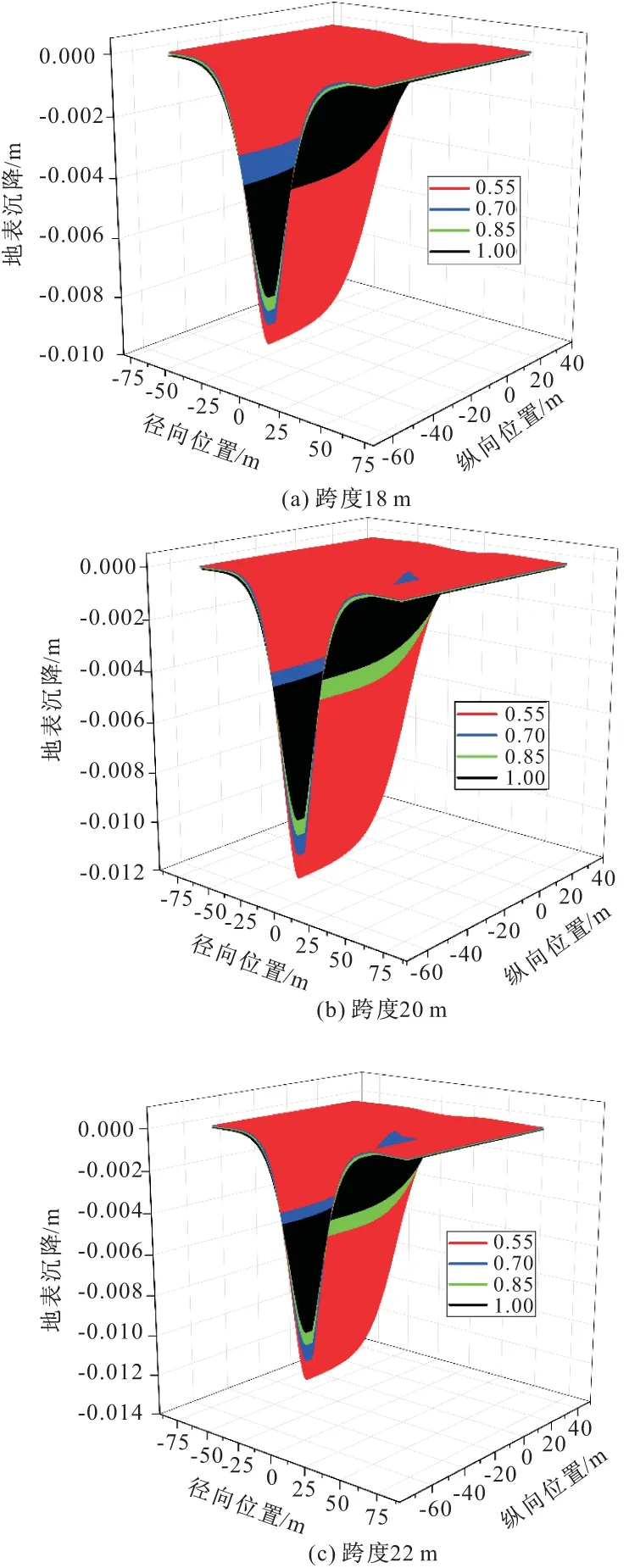
图1 不同扁平率下地表沉降曲面

由图1可知，在相同跨度下，扁平率对沉降槽宽度的影响较小，沉降槽宽度主要受隧道跨度的影响；随着扁平率的减小，隧道最终沉降值越来越大，并呈现出加速的趋势；不同跨度下，沉降槽随扁平率的变化呈现出相似的变化规律，扁平率对地表沉降的影响主要表现在宽度系数以内，相同跨度下，沉降槽的宽度系数和宽度受扁平率影响较小。

2.2 拱顶沉降和底部隆起

在对隧道变形进行研究时，选取拱顶、底部中心和两帮等四个位置点为研究对象。图2，3分别为不同扁平率条件下拱顶沉降和底部隆起曲线，图中横坐标为隧道纵向上距掌子面的距离，第四幅图为对应的最大值与扁平率的变化趋势图。

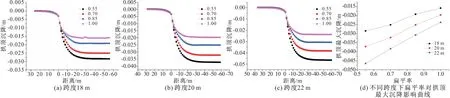
图2 不同扁平率下拱顶沉降曲线

图3 不同扁平率下底部隆起曲线

由图2可知，在相同跨度下，随着扁平率增加，拱顶沉降值越来越小，最大沉降值的减小速度呈现先加速后减速的特点，速度变化拐点与跨度有关，随着跨度的增加，该拐点对应的扁平率越来越小；在研究范围内，当跨度为22 m时，只存在减速段，加速段在研究范围以外；在距掌子面前方(未开挖)1倍跨度范围内，隧道开始发生超前变形，相同跨度下，扁平率对拱顶超前变形的影响较小；在距掌子面后方(已开挖)2倍跨度处隧道变形趋于稳定，扁平率对隧道拱顶沉降的影响主要集中在已开挖部分；跨度不同时，随着扁平率的增加，跨度间的拱顶最大沉降值差距逐渐减小；跨度越大，扁平率的影响效果越显著。单纯从对拱顶沉降控制方面考虑，拱顶扁平率应选择较大值。

图3是不同扁平率条件下隧道底部隆起曲线图，由图可知，相同跨度下，随着扁平率的增加，隧道底部隆起数值越来越大，规律与拱顶沉降相反，但超前变形范围和拱顶超前变形范围相差不大；同时随着跨度的增大，底部隆起最大值随扁平率的增加呈现出加速的现象；随着扁平率的增加，不同跨度间的底部隆起最大值相差越来越大。

2.3 两帮收敛

图4是不同扁平率下隧道两帮收敛曲线图。由图4可知，在不同跨度和扁平率条件下，两帮收敛的数值较小且相差不大；随着扁平率的增大，两帮收敛值越来越小；与拱顶沉降和底部隆起不同的是，在掌子面处，两帮收敛曲线出现了突变，随着扁平率的减小，突变越来越小，直至消失；随着扁平率的减小，跨度间的收敛差距越来越大。

由图2～4可知，单纯从控制隧道周边位移的角度来说，在设计隧道断面形状时，隧道上部应选择较大扁平率，隧道底部应选择较小扁平率，同时，对隧道的两帮尤其是拱脚位置应当采取必要的支护措施防止因位移突变发生剪切破坏。

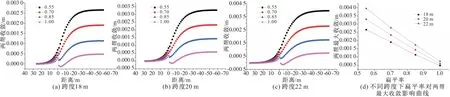
图4 不同扁平率下两帮收敛曲线

3 隧道周边围岩应力特征

3.1 主应力分析

隧道开挖后，隧道周边的围岩为抵抗岩体的不均匀变形会产生某一应力集中区域，主应力发生偏转。针对浅埋隧道上下不等压的特点，一般认为拱顶是成拱的薄弱位置，因此选取隧道拱顶至地表的竖直连线为研究对象，进行主应力分析。

图5为主应力随深度变化曲线，由图5可知，在隧道埋深为12 m时，隧道形成压力拱，不同扁平率下，压力拱的位置变化较小，并且最大和最小主应力在埋深14 m以前变化不大；在14 m以后对最小主应力影响较小，对最大主应力影响较大，在17～18 m之间，随着扁平率的减小，隧道顶部会再次出现应力集中的现象，这说明隧道扁平率对隧道周边的围岩应力状态产生一定的影响，当扁平率较小时，隧道拱肩对拱顶的支撑作用减弱；当拱顶的应力集中较大时，可能会导致围岩塌落，对隧道围岩的稳定性是不利的，在实际施工过程中应当避免该现象的发生。

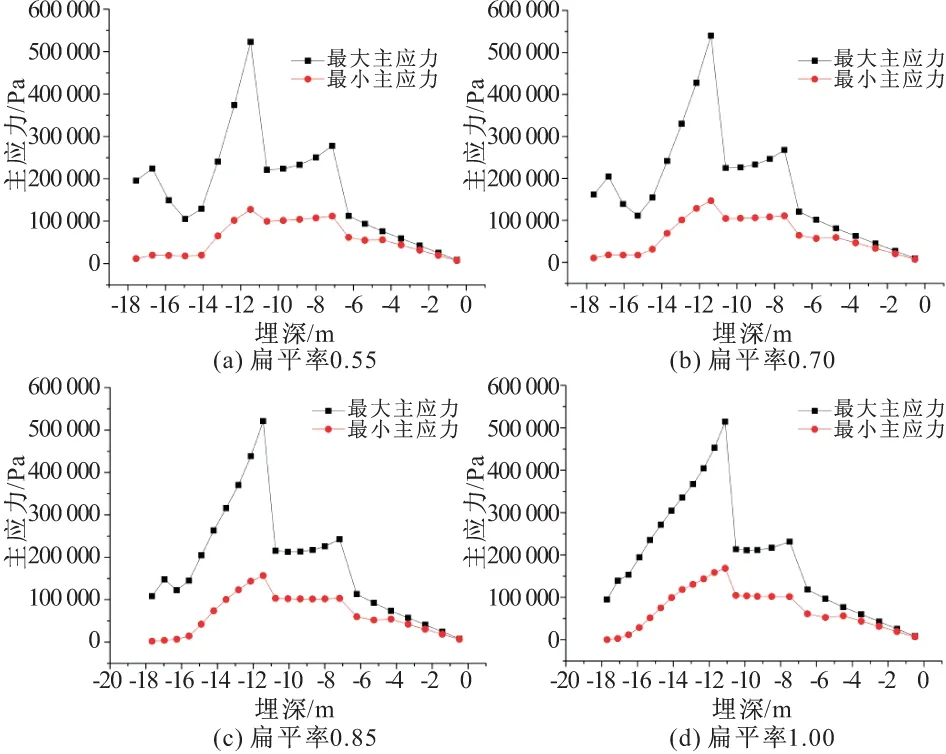
图5 主应力随深度变化曲线

3.2 塑性区分布规律

塑性区的分布范围和体积是衡量围岩稳定性的一个重要特征，图6～8分别为跨度为18，20，22 m时扁平率对塑性区分布的影响。由图可知，在隧道轴向上，相同跨度下，随着扁平率的增加，塑性区呈现出明显的上下不对称特点，隧道顶部和底部塑性区范围变化较小；同时不难发现，在隧道

图6 跨度为18 m时塑性区分布

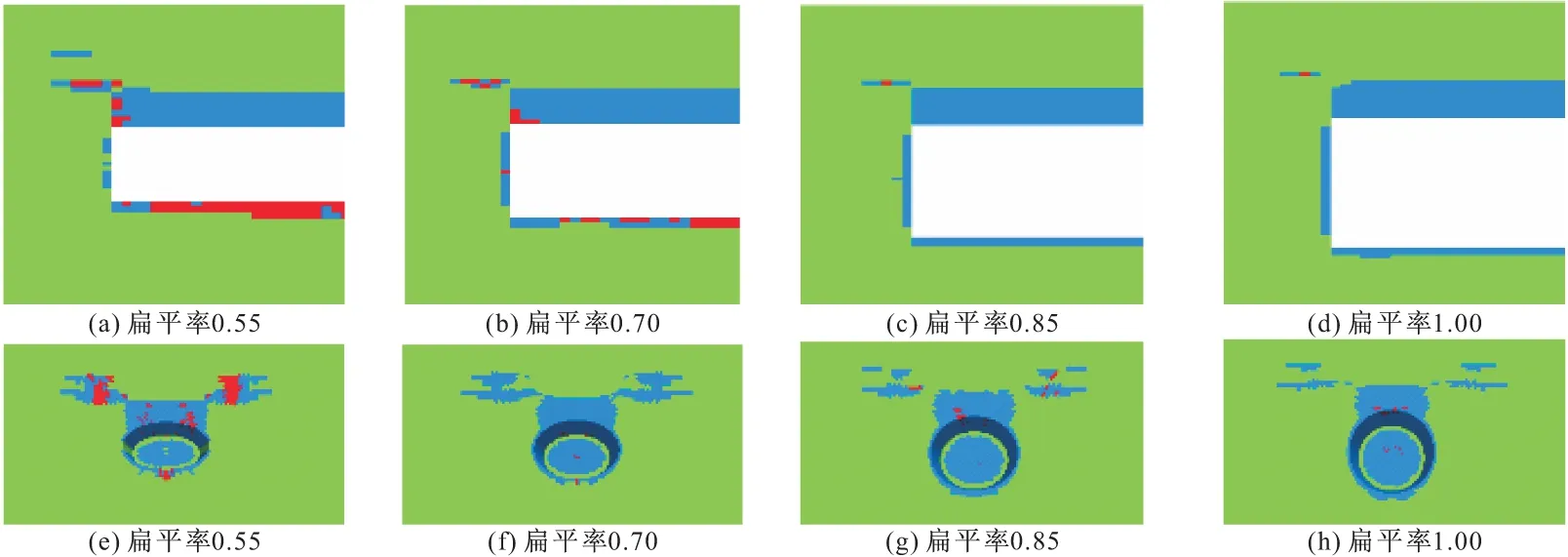
图7 跨度为20 m时塑性区分布

图8 跨度为22 m时塑性区分布

前上方(未开挖部分)出现了一定范围的塑性区，随着扁平率的增加，该区域塑性区范围逐渐减小，这说明当扁平率较大时，拱肩对拱顶的支撑作用较强，减小了因拱顶下沉而对掌子面前上方产生的拉应力。

在掌子面所在的隧道径向上，掌子面处较小的范围内也会出现一定塑性变形，掌子面处塑性区半径与隧道半径具有很好的一致性；同时，在隧道轴向上，掌子面前方塑性区与隧道径向上的塑性区并不相交。因此，在对浅埋隧道进行相关弹塑性分析时，可以认为掌子面和隧道周边塑性区分布是相互独立的，并且忽略二者的相互作用是完全可行的。

在隧道径向上，围岩塑性区分布呈现牛角状，随着扁平率的增大，隧道上方的塑性区变化较小；就隧道下方而言，随着扁平率的增加，隧道底部的塑性区分布由隧道底部两侧逐渐向隧道底部中心位置移动，这说明，当扁平率较小时，隧道底部主要受力区域并不在中心位置，而在中心位置两侧，该位置与扁平率大小有关。因此，对于隧道底部而言，调节扁平率可以改善隧道的周边应力状态，选择合适的扁平率有利于隧道的稳定。

4 隧道纵向变形曲线

由图2～4可知，不论是拱顶还是两帮，在隧道纵向上的位移曲线呈现出明显相似的变化趋势。对于浅埋隧道周边位移来说，拱顶沉降最大，是隧道周边位移监测和控制的重点。不少学者以圆形断面隧道为例，针对隧道纵向变形曲线(LDP)进行相关研究，提出了弹性和弹塑性条件下的位移释放系数公式[18～22]。

为更好的与现有理论进行对比分析，这里以扁平率为1时的隧道断面形状为例，分别对跨度为18，20，22 m的拱顶沉降曲线进行归一化处理，并与Panet[20]在1995年提出的弹性条件下隧道纵向沉降曲线和Vlachopoulus等[22]在2009年提出的弹塑性条件下隧道纵向沉降曲线进行比较，如图9所示。图中：横坐标为距掌子面的相对位置，用x/D表示，其中，x为隧道纵向距掌子面的相对距离，D为扁平率为1时的隧道半径；纵坐标为距离为x处的位移释放系数，用μ/μmax表示，其中，μ为距离为x处的拱顶沉降，μmax为隧道稳定时的最大沉降值。

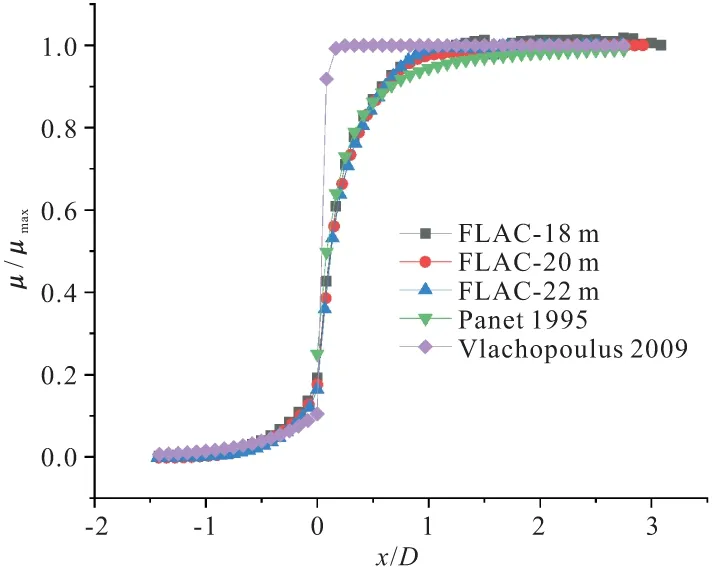
图9 隧道纵向变形曲线比较

由图9可知，不同跨度条件下拱顶沉降曲线进行归一化处理后，具有很好的拟合性。同时归一化处理后的曲线与Panet提出的曲线拟合较好，与Vlachopoulus等提出的曲线拟合稍差，这种差异主要集中在掌子面附近。整体来说，与归一化处理后的拱顶位移释放系数相比，由于Panet曲线是在弹性条件下得到的，没有考虑塑性区的影响，而在实际过程中在已开挖部分发生了塑性变形，因此由Panet得到的位移释放系数略小。而Vlachopoulus曲线考虑了塑性区的影响，并且该模型条件下隧道周边的塑性区与掌子面的塑性区相交，因此得到的位移释放系数略大。这说明塑性区分布对隧道纵向沉降曲线具有一定的影响，当塑性区存在时，位移释放系数与不存在塑性区时相比要大，并且当隧道周边的塑性区与掌子面的塑性区相交时，隧道周边位移达到稳定状态时距掌子面的距离较小，这对开挖后支护及时性提出了更高的要求。因此，在实际施工过程中，应当尽量避免或者降低掌子面前上方发生塑性变形。当纵向上隧道周边的塑性区与掌子面前方的的塑性区不相交时，Panet曲线拟合效果更好。

5 结 论

通过对不同跨度和扁平率条件下地层沉降、隧道变形和隧道周边应力分析，主要得出以下结论。

(1)沉降槽宽度主要受跨度的影响，相同跨度下，扁平率对沉降槽的宽度和宽度系数影响较小，对沉降槽宽度系数以内的区域影响较大，随着扁平率的减小，地表沉降越来越大，并且呈现出加速的变化趋势。

(2)随着扁平率的增大，拱顶沉降越来越小，底部隆起越来越大。隧道周边超前变形范围和变形稳定范围在相同的跨度和扁平率条件下具有很好的一致性。在选择隧道的扁平率时，隧道上部应选择较大值，隧道下部应选择较小值。

(3)扁平率对两帮收敛的影响较小。当扁平率较大时，两帮收敛曲线在掌子面处会发生突变，随着扁平率的减小突变越来越小，直至消失。在施工过程中应当采取必要的支护措施，防止因突变过大而发生剪切破坏。

(4)隧道拱肩对拱顶具有一定的支撑作用。随着扁平率的增大，支撑作用逐渐增强，最大主应力在拱顶的应力集中现象减小，并且隧道前上方因拱顶下沉产生的拉应力减弱。

(5)隧道周边的塑性区分布呈现明显的上下不对称性，掌子面在径向上的塑性区分布与隧道断面形状具有很好的一致性，并且在纵向上隧道周边的塑性区与掌子面上的塑性区不相交。