一种基于短文本相似度计算的知识子图融合方法

郑志蕴，吴建萍，李 钝，刘 允，米高扬

(郑州大学 信息工程学院，郑州 450001)

1 引 言

知识图谱实质上是一个语义网，清晰明确的表达了物理世界中的实体及其相互关系.目前，已经涌现出一大批知识图谱的相关产品，其中具有代表性的国外产品有谷歌公司使用的Knowledge Vault、苹果公司使用的Wolfram Alpha、智能计算引擎及Freebase等；具有代表性的国内产品有百度“知心”和搜狗“知立方”等.这些已有的知识图谱研究目标是从无/半结构的互联网信息中获取有结构知识、自动融合构建知识库、服务知识推理等.其中，知识融合是知识图谱构建的重要步骤.

知识融合在实际应用中主要以图融合的形式存在.图融合可以被认为是基于知识相似度的计算任务，通过欧式距离或余弦距离等方式计算任意两个对象之间的相似度.在已有的工作中，多是关注知识图谱中的拓扑结构而忽略了实体名称字面含义中所携带的语义信息，如图1所示.因此在图融合过程中，不仅需要考虑图的结构信息，而且需要引入语义信息.

从图1可以看出，忽略字面含义的知识图谱表示学习并不能直接预测Tom和Jane之间的关系，但是，在考虑到他们相近的出生日期以及校友关系等因素之后，Tom和Jane之间是存在潜在关系的.

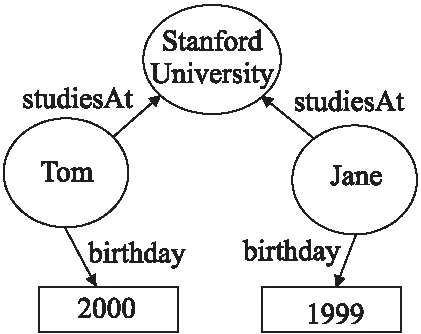
图1 携带语义信息的关联图Fig.1 Association graph carrying semantic information

为了改善学习，知识图谱逐渐被引入教育领域.在构建教育知识图谱的过程中，将概念信息引入知识表示，并得到融合后的知识子图，是一个复杂的过程.由于实体所携带的语义信息具有内容简短等特点，本文提出了一种基于短文本相似度计算的知识子图融合方法，用以解决知识子图融合中的问题.

在本文中，首先利用基于众包的知识子图获取方法，采用顶点权重和顶点关联权重占比策略对知识子图进行约简，其次通过统计词频对顶点进行二次约简，并采用图集合距离对短文本进行相似度计算；最后通过一种基于向量运算的双邻接矩阵融合方法，得到最终的高质量知识图.通过实验验证本文方法具有可行性，而且得到了较好的融合结果.

2 相关工作

2.1 知识表示

现有的知识表示方法多是关注知识图谱中的拓扑结构而忽略了实体名称字面含义中所携带的语义信息.Chen等人[1]学习低维度网络中结点的潜在表示，得到的低维度向量可以用来结点分类，对结点与结点之间的关系进行预测.Sami等人[2]提出了一种新方法，将边缘信息作为结点嵌入的函数，同时结合随机游走的信息，产生了高精度的图形结构.Rossi等人[3]提出了一种通用的归纳图表示学习框架DeepGL，用于学习跨网络概括的深度结点和边缘特征.方阳等人[4]针对知识图谱能够符号化并具备有逻辑性的特点，提出一种改进的基于翻译的知识图谱表示方法TransAH.

2.2 相似度计算

传统的文本相似度计算方法通过统计文本间共有的词语信息得到文本间的相似度，本文采用五元组来表示知识图谱中的结点，其中结点携带概念信息，由于结点携带的短文本信息只包含很少数量的词语，短文本内容简短的特性会导致数据稀疏而造成计算结果出现偏差，因此本文提出了一种基于短文本的相似度计算方法.目前图相似性的研究工作主要集中于子图的匹配，而没有充分考虑图集合之间的匹配，由于本文采用众包的方式获取数据，数据量大且冗余过多，因此本文提出了一种基于图集合距离的方法，通过结合图集合距离方法和短文本相似度计算方法，可以获得相似度较高且子图质量较高的图集.

目前TF-IDF[5](Term Frequency-Inverse Document Frequency,TF-IDF)是一个用于度量文本相似性的常用表示方法，它依赖于词的重叠，来找到相似之处，但在很短的文本上，词重叠很罕见.Miller等人[6]对语义相似度从高到低的成对名词进行研究，探讨了语义相似度与语境相似度的关系.Liang等人[7]提出了基于支配集的子图匹配算法，采用两阶段剪枝策略，加快了集合相似度子图匹配的图查询.Li等人[8]针对大多数现有的工作都是以“全局”的方式实现融合权重，提出了一种新的基于“局部”学习的属性图聚类加权的k均值算法，称为结构与属性信息的自适应融合Adapt-SA(Adaptive Fusion of Structual and Attribute Information,Adapt-SA).Zeng等人[9]建立了一个星形模型，采用多项式时间来计算上下界，在考虑图的数量和大小的情况下，实现了图搜索问题.庞俊等人[10]针对目前图相似性的研究工作主要集中在子图的匹配上，而没有充分关注图集合之间的匹配，提出了一种基于过滤-求精框架的GSSS算法.詹志建等人[11]通过对短文本建立复杂网络模型，计算出短文本词语的复杂网络特征值再借助外部工具计算得出短文本词语之间的语义相似度.宋冬云等人为提高中文短文本相似度计算的准确率，提出一种新的基于混合策略的中文短文本相似度计算方法.张培颖等人[12]将义原树之间的最短路径作为衡量两个义原之间的语义距离的依据，然后把义原距离转换为义原相似度，提出了一种多特征结合的词语相似度计算方法，实验验证了算法的有效性.

2.3 知识图融合

在知识融合过程中，由于知识来源广泛，质量难以判定，其中可能包含大量的模糊、歧义、冗余甚至错误信息，而对于带有标签的图更是包含了结构信息和语义信息，这两种不同类型的异构信息加大了融合的难度.Wang等人[13]提出了一种用于卡消歧的新概率评分算法，以选择卡来参考最可能的实体，设计一种基于学习的方法来对齐代表同一实体卡片的属性.Cheng等人[14]基于知识图的广泛应用和教育领域日益增长的需求，提出了一种基于知识图的教育知识图谱自动构建系统.Sun等人[15]研究了一种更实用的设置，即对知识库和实体链接文本的组合进行QA.Nie等人[16]通过医师专业知识分布和专业知识问题分布的概率融合来弥合专业知识匹配差距.郭芳等人[17]采用众包技术进行知识资源的获取，并提出了基于矩阵运算的知识子图融合方法.吴笑凡等人[18]提出了基于分布式主题图融合的TOM(Topic & Occurrence-Oriented Merging,TOM)算法，通过判断不同主题图中的主题是否指示同一项目，检查它们所表示内容的相似性程度以实现融合.

3 相关定义

定义1.(传统子图集).知识子图集G={G1,…,Gi,…},Gi=(VG,EG,WV,WE).其中VG为知识图谱的顶点集合，每个结点v∈VG；EG⊆VG×VG表示知识图谱的边集合，每条边e∈EG用无向的直线表示；WV是顶点权重集；WE是边权重集.

定义2.(二分图).在知识子图Gi中，如果顶点V可分割为两个互不相交的子集V1和V2，并且Gi中每条边e所关联的顶点v1，v2分别属于这两个不同的顶点集，则称为二分图.

定义3.(二分图最小完美匹配).在二分图Gi中，每条边e互不相交且满足e的权重最小，若覆盖了二分图的所有顶点，则为二分图的最小完美匹配.

定义4.(图集合对最小二分图匹配).已知两个图集合S(ui)和S(vj)可以构成二分图，S(ui)表示包含图ui的集合，S(vj)表示包含图vj的集合，S(ui)和S(vj)分别对应二分图中的V1、V2集合，S(ui)或S(vj)中的每一个图对应V1或V2中的一个顶点，若两集合中的基数不相等，则在基数较小的图集合中补充虚拟图，使得图集合对等.

定义5.(图集合距离).由图集合S(ui)和S(vj)得到的最小二分图匹配数，则为图集合距离d.

定义6.(标签子图集).在传统子图集中引入标签数据集L={l1,l2,…}，L中主要描述的是知识图谱Gk中集合VG的顶点对应的标签概念信息，数据中的一条记录Li可以表示为{Vi,Ti},其中Vi表示知识点，Ti={t1,t2,…}表示vi对应的标签集，此时G={G1,…,Gi,…},Gi=(VG,EG,WV,WE,L).

4 一种基于图集合距离的短文本相似度计算方法

本节将以计算机学科的子图获取为例，结合众包思想，获取个体知识子图，在获取子图之后，主要通过子图降噪和相似度计算，对知识子图进行预处理并融合.首先，根据子图的顶点权重值和顶点关联权重值，采用基于加权策略的子图降噪算法对其进行约简处理；其次，对具有相同顶点数的子图进行同等划分，得到若干图集合，并对其进行图集合相似度计算，将获取的候选结果集进行求精；最后，通过对集合内各个子图的顶点所携带的标签含义进行短文本相似度计算，得到最终有效的图集.

4.1 基于众包的知识子图获取方法

本节结合众包思想，首先学习者根据已学过的课程并加入自己的理解构建属于自己认知范围内的个体知识子图；其次学习者还可对关键知识点进行更新，迭代知识联想过程，如果发现有新的关系无法用已有的关系表达时，便说明这是一个新的关系需要补充，如果发现有新的概念无法利用已有的概念替代时，便说明这是一个新的知识需要补充.最后根据知识子图对关键知识点进行更新，迭代知识联想过程，获得个体知识子图集G={G1,G2,…,Gi,…}.

4.2 子图降噪

通过众多学习者得到的数据普遍具有冗余性，本节将对第4.1节获取的子图集进行降噪处理，采用顶点权重和顶点关联权重占比策略对子图进行约简，再通过统计词频对顶点进行二次约简.

1)子图约简

首先学习者k根据子图Gk的顶点集及顶点关联集的大小，得到顶点个数|VG|和边个数|EG|；然后通过公式(1)和公式(3)计算，得到Gk的顶点权重WV(Gk,Vi)和边权重WE(Gk,Vi,Vj)；最后依据权重比，筛选出具有重要知识点与知识关联的子图集.顶点权重计算如公式(1)所示.

(1)

其中，Gk表示学习者k构建的子图，W(Gk,Vi)表示Gk的顶点权重之和，若权重和越大，则说明图中包含的重要知识点越多，该学习者构建的知识子图整体质量越高.vi表示第i个顶点，|WVi|表示第i个顶点的权重，n表示Gk的顶点个数，即|VG|.

本节将边权重计算分为两步，先对边权重进行初始化，如公式(2)所示；再根据学习者k构建子图的关联权重对边权重进行更新，如公式(3)所示.

(2)

其中，WE(Gk,Vi,Vj)表示vi与vj是否存在相连的边，若子图Gk中vi与vj有边相连，则WE(Gk,Vi,Vj)值置为1；否则，置为0.

(3)

其中，WE(Vi,Vj)表示边(vi,vj)的权重，n表示Gk的顶点个数.

通过得到的顶点权重值与边权重值，采用基于加权策略的子图降噪算法(Subgraph Denoising Algorithm Based on Weighting Strategy,SDWS)对子图集G进行降噪处理，如算法1所示.

算法1.基于加权策略的子图降噪算法(SDWS)

输入：子图集G

输出：子图集G*

1.给定初始值p←m,i←1,j←1,λ∈(0,1) ;

2.while(p≥1)

3.while(i≤n&&j≤n)

4. 通过式(1)计算顶点权重WV(Gk,Vi)；

5. 通过式(3)计算边权重WE(Gk,Vi,Vj)；

7.a[n]=k;

8.G*←G-Gk;

9.endif

10.i++；

11.endwhile;

12.p--;

13. go to step 2;

14.endwhile;

15. 输出G*；

16.end;

在算法1中，结合顶点权重和边权重，剔除质量较差的子图.在1中，p表示图的个数，i，j均表示图的顶点个数且i≠j，设置阈值λ来判断图中含有的重要知识点和知识关联的比重；在3中，n表示当前图的顶点个数；在4、5 中，Gk表示学习者k构建的子图；在7中表示将构建质量差的子图所属的学习者记录在数组a中，并给出一定的评分；在8中表示将无用子图剔除.重复上述过程，得到高质量的知识子图集G*.

2)顶点约简

首先对每个知识点的出现频率进行统计，将词频小于阈值γ的知识点过滤以后，得到集合V′.然后对V′进行人工筛查，剔除其中的噪声词.为了降低人工筛查的难度和工作量，将V′与现有大规模词库比对，取二者交集V″之后再进行人工筛查.因为大规模词库通常都是行业公用的词典，词汇量大且较为全面，可信度高，因此先将V′与大规模词库取交集，可以大大缩小V′的规模，有效减少人工筛查的工作量.经过上述一系列的预处理过程后，得到有效知识点集合V′={v1,v2,…,vn}.

4.3 基于图集合距离的短文本相似度计算方法

在知识子图集中，结构相似的图所对应的顶点和边具有相似的表达含义，目前大部分学者忽略了顶点所携带的结构信息和语义信息.本节提出了基于图集合距离的短文本相似度计算方法，首先，根据图集合距离，构建完全二分图，用图集合相似度搜索策略获取较小的候选结果集；其次，通过对子图顶点所携带的语义信息进行预处理，计算出各个词语结点的综合特征值，得到短文本相似度；最后，对两种相似度进行加权，得到最终的相似度.

结合SDWS算法中得到的子图集G*，并对其进行划分，将具有相同顶点数的子图划分到同一个集合中，得到若干子图集S={S1,S2,…,Sm}(其中m为集合个数)；其次，通过扩展的KM算法求解S中集合对间的最大完美匹配，若匹配数小于等于t，则两个集合相似[10]，此时知识子图集G**={s|d(s,si)≤t,s∈S,i∈(1,m)}，其中，t表示距离阈值，si表示第i个图集合，d(s,si)≤t表示从集合S中的所有图集合里，找出与si集合间的距离小于等于t的集合，并将集合对相似的集合存到G**中.

由于得到的图集G**中的每个图的顶点均携带语义信息，只要文本相似，那么文本中的词语在一定程度上也是相似的，而文中的标签信息具有内容简短、数据稀疏等特点，采用传统的文本相似度计算方法可能会引起计算结果出现偏差.本文借助现有的工具对中文短文本进行预处理，对其进行分词、词性标注、停用词过滤等操作.然后，根据短文本建立复杂网络模型，计算短文本词语的复杂网络特征值，再借助外部工具计算短文本词语之间的语义相似度[11]SimST(Gk l1,Gkl2)，其中Gkl1表示Gk中顶点V1所携带的文本信息，Gkl2表示Gk中顶点V2所携带的文本信息.若得到的相似度大于μ，其中μ表示词语相似度阀值，则视为文本相似，否则视为不相似，得到最终的结果集G***.

5 基于向量运算的双邻接矩阵融合方法

知识子图融合是指将若干学习者自主构建的缺少完整性和缺乏准确度的知识子图经过有效的处理，生成较为完整和标准的群体知识图谱的过程.标签图与传统图有一定的不同，前者包含了两种不同类型的异构信息，即结构信息和语义信息.结构信息表示结点间的联系，语义信息表示每个结点上携带的标签信息.本节提出了基于向量运算的双邻接矩阵融合方法，用来平衡各结点的结构连接和标签信息，得到具有高属性语义相似性的最终知识子图.融合过程可以分为5个步骤：

1)根据公式(3)计算得到的知识关联权重WE(Gk,Vi,Vj)，将知识子图转换为知识子图关联权重矩阵En×n=(E1,E2,…,En)，如公式(4)所示.

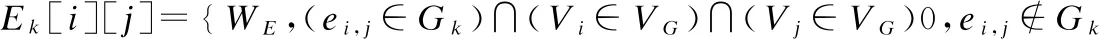
(4)

其中，WE表示Gk中Vi和Vj间的关联权重，Ek[i][j]表示若Gk中知识点有边相连，则矩阵值为边的权重WE；否则，矩阵值为0.

2)根据用邻接矩阵A=(A1,A2,…An)表示顶点语义信息，如公式(5)所示.

Ak[i][1]=Ti，Vi∈Gk

(5)

其中，Ti表示Gk中第i个顶点Vi所携带的标签信息，即语义信息，Ak[i][1]表示用n×1的矩阵将知识子图的语义信息进行存储.

3)由于结点的标签都是短文本，因此本节采用第4.3节计算得到的短文本相似函数SimST(Gk l1,Gkl2)，将知识语义信息矩阵转换为知识语义信息相似度矩阵，如公式(6)所示.

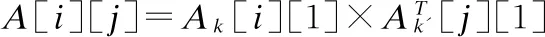
(6)

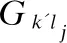
4)对图G***中每个图都做上述处理之后，将每个结点vi∈vG的这两个信息组合起来，得到一个联合表示.通过设置一组权重向量α=(α1，α2，…,αn)T,αi∈[0,1]，得到融合后的矩阵，如公式(7)所示.

EAk=Ekαi+Ak(1-αi)

(7)

通过将子图转换为二维矩阵，采用基于向量运算的双邻接矩阵融合方法(Double Adjacency Matrix Fusion Algorithm,DAMF)对子图集G***进行融合处理，如算法2所示.

算法2.基于向量运算的双邻接矩阵融合方法(DAMF)

输入：子图集G***

输出：融合矩阵EAk

1.给定初始值En×n，An×1，m,i,j，k;

2.while(k≥1)

3.for(i←0；i≤m；i++)

4.for(j←i+1；j≤m；j++)

5. 通过公式(3)计算得到知识关联WE(Gk,Vi,Vj)的值；

6. 通过公式(4)将Gk转换为知识关联权重矩阵Ek[i][j]；

7. 通过公式(5)将Gk转换为知识语义信息矩阵Ak[i][1]；

8.endfor;

9.endfor;

10.if(k≥2)

11. 根据第4.3节计算得到短文本相似度函数 SimST(Gk-1 l 1,Gkl2)；

12. 通过公式(6)将Ak[i][1]转换为Ak[i][j]；

13. 设置一组权重向量α=(α1,α2，…,αn)T；

14. 通过公式(7)计算出融合矩阵EAk;

15.endif;

16. k--;

17.endwhile;

在算法2中，结合向量运算，用邻接矩阵的形式存储子图，对子图进行融合.在1中，En×n表示n行n列的矩阵，An×1表示n行1列的矩阵，m表示Gk中顶点的个数，i，j均表示顶点的初始值,k表示子图的个数.重复上述过程，得融合后的矩阵.

综上，通过子图降噪与基于图集合的短文本相似度计算加快了融合的过程,并且使用结点缩略图大大减少了再次查询的时间代价.由于在构建知识图谱过程中需要专家的协助，特别是针对特定领域的知识图谱更需要专家提供的专业知识.因此，在课程数据采集原型平台中，教师可以对融合后的课程知识图谱进行完善修正，得到最终完整的知识子图.

6 实验结果与分析

6.1 数据采集

为了获取真实的数据集，本文构建了一个计算机学科内的课程数据采集原型系统，采用众包的方式，组织30位学生对已学过的某门课程根据自己的理解构建个体知识子图.在构建的过程中，表1介绍了部分知识点数据采集，表2介绍了部分知识关联数据采集，图2介绍了课程知识图谱数据采集界面.在真实环境的背景下，共得到2036个知识点和3814条知识关联，来验证子图融合的效果.

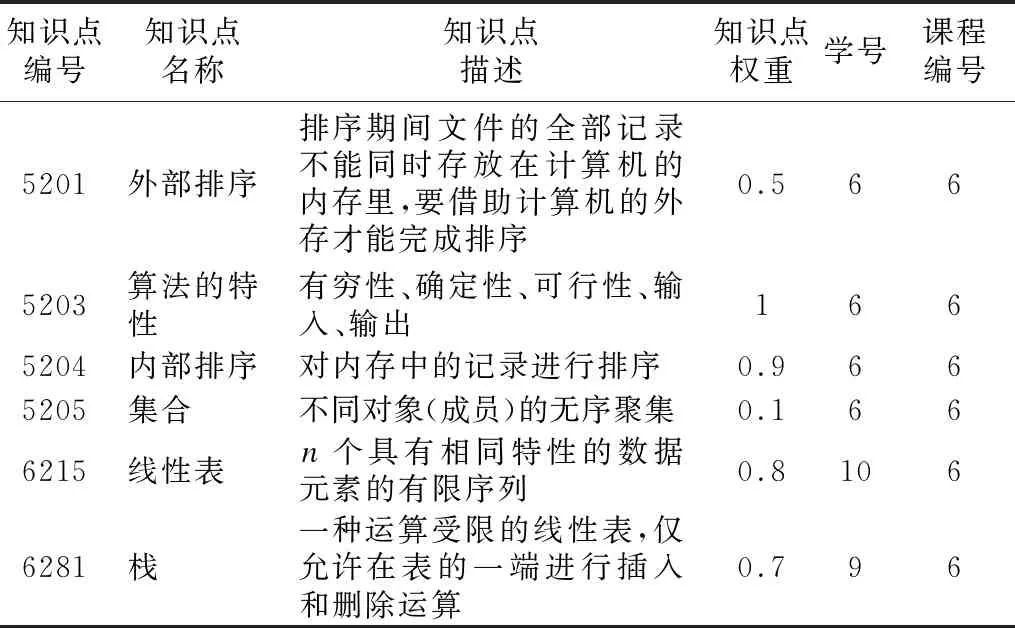
表1 知识点部分采集示例Table 1 Knowledge point part collection example

表1介绍了以数据结构为中心知识点向四周辐射的所有知识点，其中包含了学习者Gk、课程号、知识点名称、知识点权重、知识点描述等.在对知识点进行扩展的过程中，对数据结构中心知识点进行描述，使得学习者能够学习整个以数据结构为中心知识点的知识图谱.

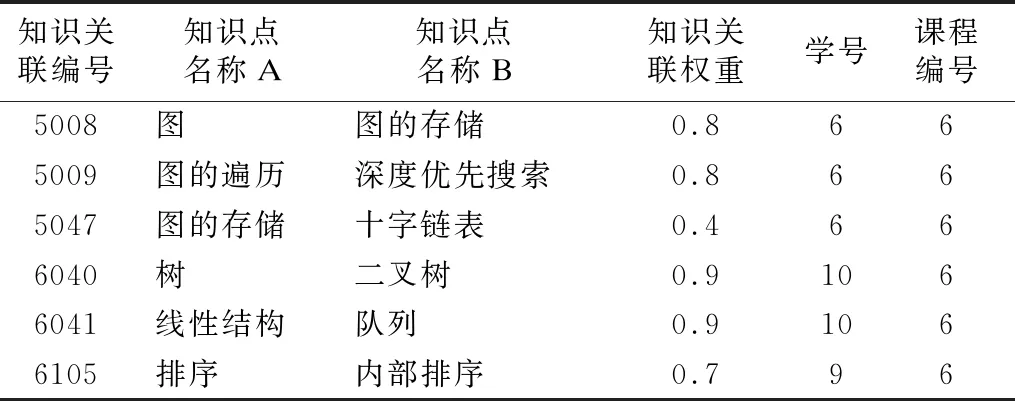
表2 知识关联部分采集示例Table 2 Link acquisition part collection example

表2介绍了以数据结构为中心知识点向四周辐射的所有知识关联，其中包含了学习者Gk、课程号、知识点A、知识点B、知识关联权重等.知识关联主要介绍了课程内知识间的紧密程度，使得学习者能够理清课程脉络，搭建属于自己的知识框架，构建完整的课程知识图谱.

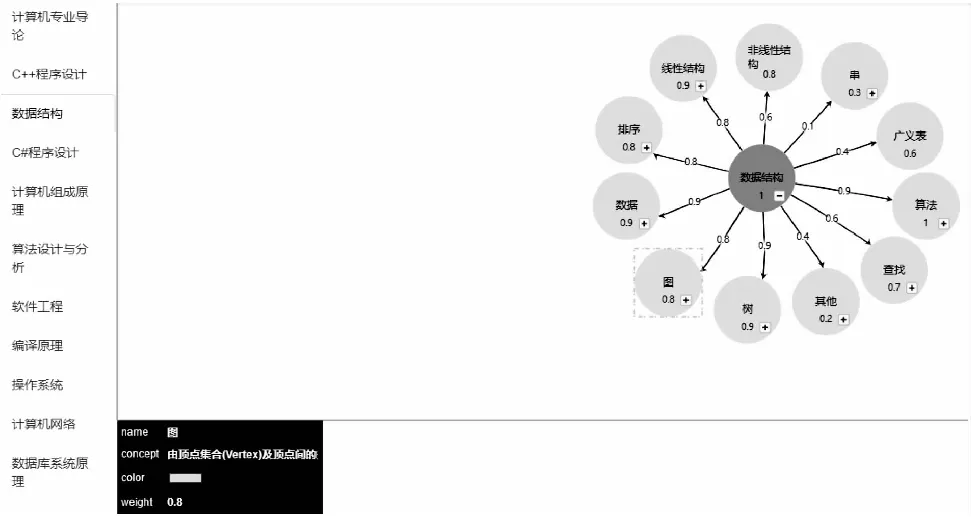
图2 课程知识图谱采集界面Fig.2 Course knowledge graph collection interface

图2介绍了整个课程知识图谱的数据采集过程，对每个知识点都有相应的概述和权重，权重表示了知识点的重要程度，在课程知识图谱采集界面内包含数据结构在内的多种课程，如软件工程、编译原理等，能够为学习者提供详细的多课程知识点表示，为学科知识图谱的构建打下基础.

6.2 实验对比

本节对课程知识采集得到的个体知识子图进行子图约简.子图约简是对原始知识图谱进行处理，在保持原始知识图谱所表示的知识体系不变的情况下，去除冗余的知识子图.本节采用SDWS算法对获得的子图进行约简，将不同知识点权重比和知识关联权重比进行实验，确定最优的阈值，如图3所示.

从图3可以得出，阈值λ(包含知识点权重比和知识关联权重比)的选取对约简图数量是整体负相关的，即随着约简图数量的变小，知识点权重比和知识关联权重比的计算数值逐渐变大.在知识图约简到达200时，知识点权重比和知识关联权重比已经趋于不变，此时计算得出知识点权重比的值在[0.52，0.55]之间，知识关联权重比的值在[0.51，0.56]之间，最终取阈值λ=0.54即为对原始知识图数据的最大约简效果.在约简的过程中，将知识点权重占比或知识关联权重占比小于0.54的子图删除，去除无效的知识子图.然后对剩余的知识子图进行相似度计算，得到高密度的知识子图集.

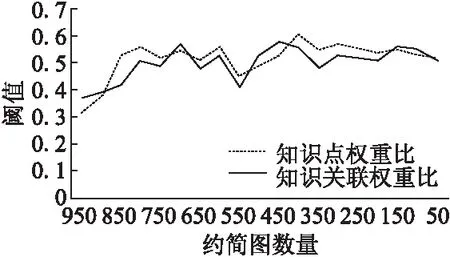
图3 阈值选取Fig.3 Threshold selection

本文提出基于图集合距离的短文本相似度计算方法，既考虑图集合之间的结构信息，又考虑了结点所携带的文本概念信息.传统的TF-IDF方法可以应用在短文本相似度计算中，但实验表明其F度量值较低，这是因为TF-IDF方法只考虑词语的TF-IDF值而未考虑词语的上下文信息.最长公共子序列(Longest Common Subsequence，LCS)[19]方法主要用于计算两个字符串的最大公共子序列的长度，但公共子序列不一定连续，它要求出现的次序相同.传统的向量空间模型(Vector Space Model，VSM)[20]主要计算文档相似度，未考虑到词语语义距离.编辑距离算法(Levenshtein Distance，LD)，主要用于两个字符串之间，由一个转成另一个所需的最少编辑操作次数，但未考虑语义间相关关系.基于图集合距离的相似度计算方法，能够进一步对知识子图进行约简，并且能够计算图之间的相似度关联函数值，其与TF-IDF、LCS、VSM、LD方法的对比实验结果如图4所示.

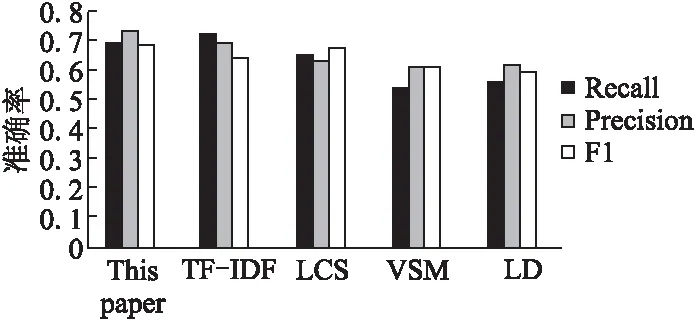
图4 不同短文本相似度计算方法对比Fig.4 Comparison of different short text similarity calculation methods

在图4中，通过查全率(Recall)、查准率(Precision)、F度量(F1)三个指标进行评价，本文提出的基于图集合距离的相似度计算方法在查全率和F1值上均优于其它方法，在查准率上略低于TF-IDF方法，主要原因是TF-IDF方法考察了所选特征出现的频率.

通过图集合距离和短文本相似度计算方法相结合，得到了图间的相似度函数，同时获得了相似度高的知识子图集.在此基础上，将获得高质量高密度的知识子图转换为双邻接矩阵，得到融合后的知识子图.本文提出VDMF算法，同时均衡了知识子图的结构信息和语义信息，将知识表示所携带的短文本概念转换为概念矩阵，利用图集合距离相似度计算方法得到语义相似度，再将知识点、知识关联等信息转换为语义信息相似度矩阵，通过向量运算得到融合后的知识子图.

为了验证VDMF的有效性与准确性，对比了不同算法构建知识图谱的效果.郭芳[20]提出一种单矩阵融合算法(VDSE)，将知识图转换为矩阵，图中有边相连，矩阵值为1；无边相连，矩阵值为0.由于其未考虑图中顶点携带的语义信息，同时也未考虑顶点的重要程度，因此DAMF算法将权重作为矩阵值，更好的突出知识点重要性及知识关联紧密度.与此同时，将VDMF算法与逻辑回归算法(Logistic Regression，LR)、支持向量机算法(Support Vector Machine，SVM)、决策树算法(Decision Tree，DT)作对比，如图5所示.

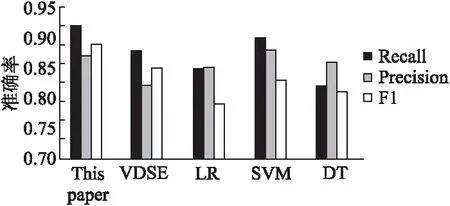
图5 双矩阵融合算法对比Fig.5 Comparison of double matrix fusion algorithms

在图5中，本文提出的双矩阵融合算法在查全率和F1值上较大幅度优于其它算法，但在查准率上略低于SVM算法，这是由于本文提出的算法在对所有知识点检索过程中得到的总知识点数与SVM计算得出的总知识点数有差异，优化并弥补实验过程中的差异也是下一步的研究方向.

7 总 结

面向在线教育领域的研究是一个既有学术意义又有应用价值的研究方向，随着知识图谱的发展，越来越多的组织及个人参与到在线教育相关的研究中.而如何发挥每位学生的主观能动性，激励学生自主学习，成为一项挑战.本文采用众包的方式获取学习者对课程的掌握程度，以玩乐的方式在平台上画一个自己认知范围内的课程体系结构，通过VDMF算法在融合效率可以接受的情况下，实现了相对较好的效果.但是本研究中也存在一些需要完善的地方，由于知识结构体系包含非常丰富的内容，从中还可以提取出其它有价值的信息，比如知识关联类别、知识点前驱后继关系等，甚至后期可以将课程内知识点融合扩展到课程间知识点融合，形成一个学科知识图谱.总之，知识图谱是一个在理论体系和应用技术两方面都非常有研究价值的领域，需要探索和提升的空间还很大，值得后续学者为之不断努力.