一种嵌入PCA特征算法在PMI指数中的应用研究

2020-01-08宋家东张芹娥刘一丹陈曙光

互联网天地 2019年10期

□ 文宋家东张芹娥刘一丹陈曙光

1 引言

PMI（Purchasing Manager’s Index）指数体系又称采购经理指数，是由中国物流与采购联合会与国家统计局于2005年共同推出的指数体系，它在每个月的第一个工作日发布，具有及时性特征，PMI体系主要由新订单、生产量、从业人员、供应商配送以及原材料库存等反应制造企业生产活动的细分指标构成，是衡量我国工业经济发展的主要指标。该指数反映了世界各个国家的主要经济变化趋势，是国际上通用的宏观经济先行性指数，对经济活动的预测与监测起到了重要作用。很多学者也都证明PMI对GDP有着很好的预测作用，而GDP则为评价和衡量国家经济状况、经济增长趋势以及社会财富的经济表现提供了最为综合的尺度，是影响经济生活乃至社会生活最重要的经济指标。

然而，PMI依然存在以下问题值得进一步研究和探讨。其中一个较为突出的问题是PMI指数的计算方式完全依赖于5个指标（订单、生产、雇员、配送、存货）以及5个经验权重参数，而这5个经验权重参数的给予是否合理，是否可以适应并反映国家的调控政策依然是个研究的课题。

围绕上述的现状，本文首先将在第2部分分别对PMI指数和主流子空间算法PCA进行阐述；在第3部分，将介绍基于嵌入PCA特征的PMI指数算法；在第4部分，对基于嵌入PCA特征的PMI指数（PCAPMI）与传统PMI指数算法进行实验对比和分析；最后，在第5部分，对PCAPMI算法研究进行归纳和总结。

2 相关算法

本章首先介绍传统的PMI指数，并给出PMI指数的定义；其次将介绍传统基于子空间技术的PCA算法，并详细阐述PCA算法的定义以及公式推导过程。

2.1 PMI指数

PMI指数定义：PMI是一个综合指数，由5个扩散指数加权而成，即：产品订货（简称：订单）、生产量（简称：生产）、生产经营人员（简称：雇员）、供应商配送时间（简称：配送）、主要原材料库存（简称：存货）。这5个指数是依据其对经济的先行影响程度而定，各指数的权重分别是：订单30%，生产25%，雇员20%，配送15%，存货10%。

令x=[x1,x2,x3,x4,x5]T,w=[w1,w2,w3,w4,w5]T其中，x为指标参数向量，x1：订单，x2：生产，x3：雇员，x4：配送，x5：存货；w为权重因子参数向量，w1：30%，w2：25%，w3：20%，w4：15%，w5：10%。具体公式如（1）所示：

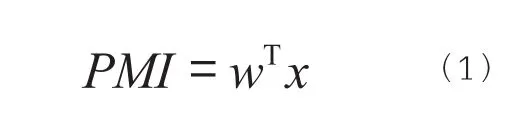
通常PMI指数会以0.5作为经济强弱的分界点，PMI高于50%时，反映经济总体扩张；低于0.5，则反映经济总体收缩。

其中，PMI单个指标汇总一般涉及生产量、产品订货、出口订货、现有订货、产成品库存、采购量、进口、购进价格、主要原材料库存、生产经营人员、供应商配送时间等11个问题，而原材料订货提前的天数单独处理，开放性问题不参加计算。它的汇总方法分为加权和不加权两种方法。

采用加权计算百分比：以国家统计局《企业基本情况调查表》的上年营业收入作为权重，计算“增加”、“基本持平”、“减少”选项所占百分比。

采用不加权计算百分比：直接根据企业个数计数，计算“增加”、“基本持平”、“减少”所占的百分比。

计算各项（“增加”、“基本持平”、“减少”）百分比时，剔除掉无关的数据项（如：“不易预估”、“没有出口”、“没有进口”等内容），即“增加”、“基本持平”、“减少”三项的百分比之和为100%。

PMI指标的计算方式采用扩散指数法，即：正向回答的百分数加上回答不变的百分数的一半。计算公式如下：

图1 PCAPMI算法流程图

2.2 PCA算法

PCA算法是一种基于非监督的算法，可以看作是在嵌入空间中寻找一个由k个包含数据最大方差方向组合的集合，即：Karhunen-Loève变换。

具体PCA算法如下：

首先，给出协方差矩阵，如（3）式所示：

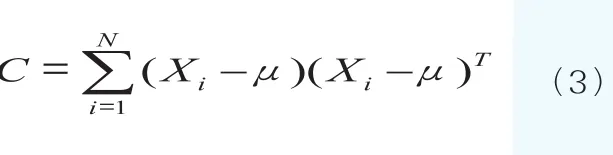
其中，Xi代表第i个样本矩阵，μ代表总均值矩阵。

然后，根据广义Rayleigh商，如（4）式所示：

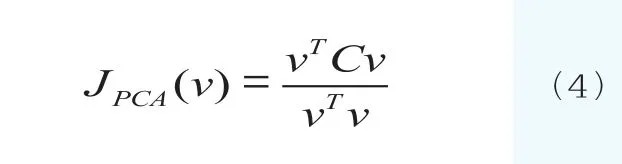
对（4）式使用拉格朗日乘数法求极值，得到PCA算法的特征方程式，如（5）式所示：

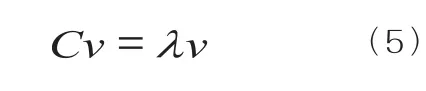
根据（5）式，求取PCA的特征值矩阵和特征向量矩阵。

3 PCAPMI算法

3.1 PCAPMI算法流程

PCAPMI算法流程如图1所示：

Step1：使用式（2）汇总并计算x1：订单，x2：生产，x3：雇员，x4：配送，x5：存货，五项的PMI指标值；

Step2：汇总收集上来的PMI指标值并以x=[x1,x2,x3,x4,x5]T向量的方式进行展示，并将采集样本以x的方式进行汇总，X=[x1,x2,x3,…,xn]；

Step3：对X采用归一化处理，将值锁定在[0-1]之间；

Step4：采用式（3），计算协方差矩阵C，并根据式（5）的方式计算，特征向量矩阵V以及特征值矩阵Λ；

Step5.1：取Λ特征值矩阵中最大特征值所对应的特征向量v，忽略其他特征值以及其所对应的特征向量，令为指标向量的均值向量，采用式（6）的类欧式距离方式计算PCAPMIappro指数（即：近似的PCAPMI指数）；其中，PCAPMIappro指数高于0.5，反映经济总体扩张；低于0.5，则反映经济总体收缩。

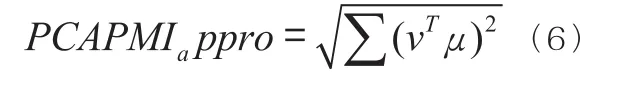
Step5.2：取Λ特征值矩阵中特征值大于零所对应的特征向量V矩阵，忽略为特征值为零对应的噪声数据，令为指标向量的均值向量，采用式（7）的类欧式距离方式计算PCAPMI指数；其中，PCAPMI指数高于0.5，反映经济总体扩张；低于0.5，则反映经济总体收缩。

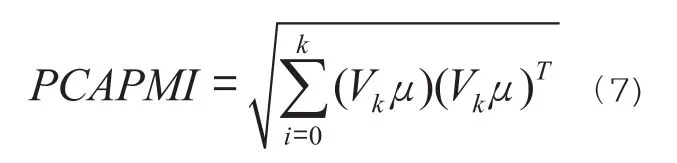
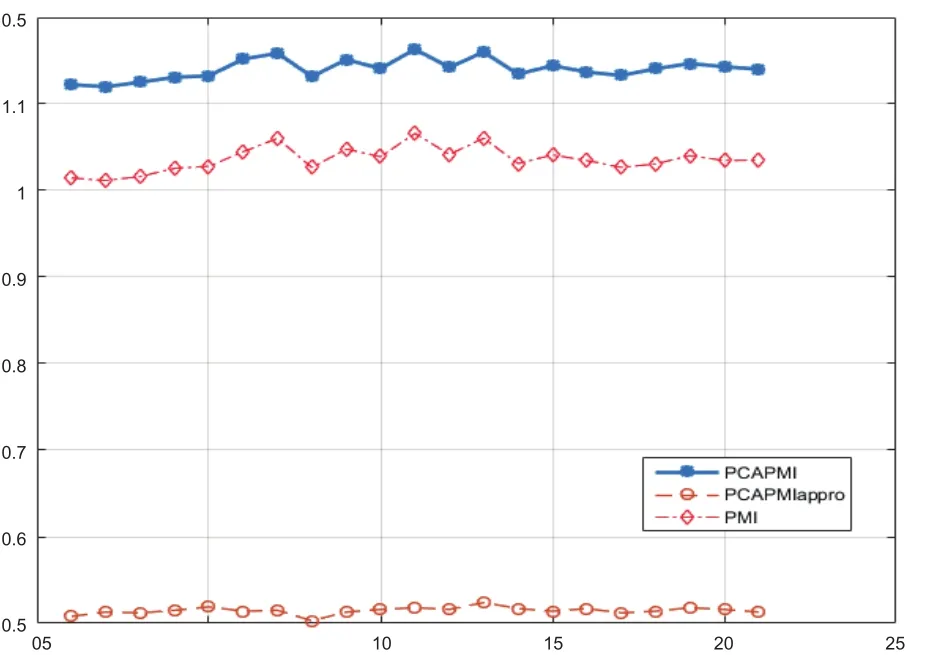
图2 PCAPMI、PCAPMIappro算法指数、PMI指数对比

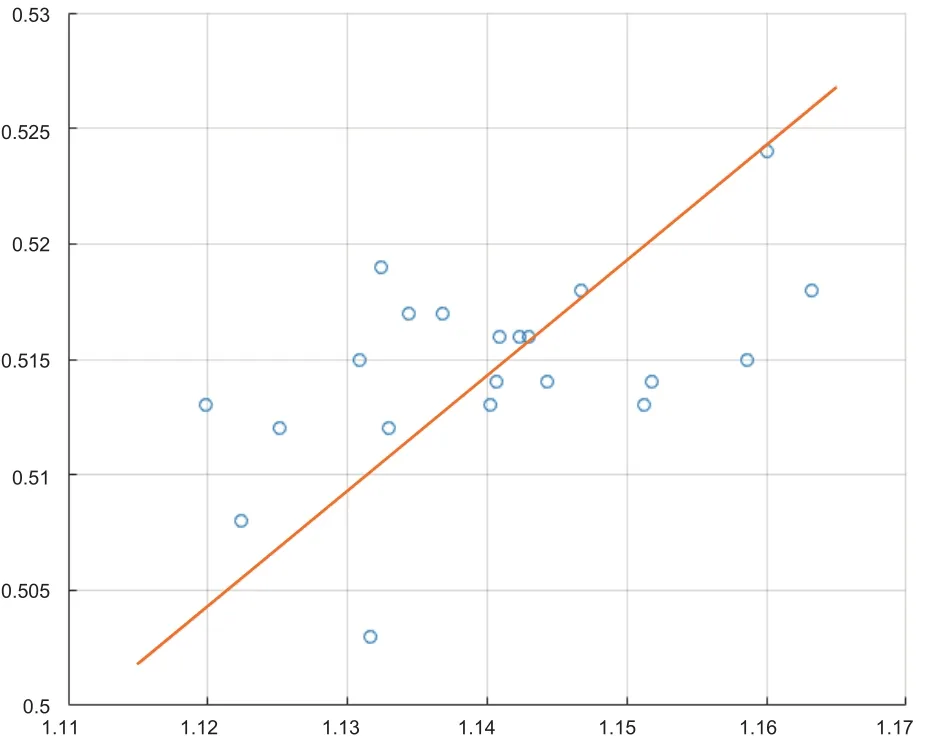
图3 PCAPMI指数与传统PMI指数存在正相关关系

4 实验

本节首先介绍实验环境以及所采用的数据库；其次，将对比传统PMI指数与PCAPMI、PCAPMI算法指数，并阐述基于PCAPMI算法的优越性。

4.1 实验环境

实验采用2017年01月至2018年09月的历史PMI指数数据作为目标数据，2017年01月至2018年09月各省企业提交的问卷并整理的指标数据作为训练数据，训练数据的指标包括：产品订货（简称：订单）、生产量（简称：生产）、生产经营人员（简称：雇员）、供应商配送时间（简称：配送）、主要原材料库存（简称：存货）。

4.2 实验分析

如图2所示，为了较为明显的表现PCAPMI算法指数与传统PMI指数的差异，以及影响PCA算法原本的计算能力，本实验没有针对PCAPMI指数算法进行最后的归一化处理，直接针对原始数据进行操作，基于PCAPMI以及PCAPMIappro计算的指数相对于传统PMI指数对数据更加敏感，峰值起伏相对PMI影响也较大，另一方面，从图中可以看出，基于PCAPMI以及PCAPMIappro算法的指数相对于传统PMI指数具有一定的前置性，能够提前较好地提醒指数的使用者对未来经济进行防范和指导相关的决策。

如图3所示，其中散点图的x轴代表官方发布的传统PMI指数，散点图的y轴代表未经预处理计算出的PCAPMI指数的统计指数，可以发现，PCAPMI指数与传统PMI指数存在正相关的逻辑关系，因此以PCAPMI指数来代替PMI指数从业务上是可行的。