联合动静力的桥梁模型分步修正方法

2020-01-07刘永淼

福建交通科技 2019年6期

刘永淼

(厦门轨道交通集团有限公司，厦门 361004)

目前桥梁结构承载能力评定主要是通过静动载试验和有限元计算[1-2]对结构受力、变形等状况进行分析。桥梁荷载试验能够直观反映出桥梁结构在试验荷载作用下上部结构的整体受力性能，得到桥梁结构截面应力、位移等数据，并结合桥梁实际情况对桥梁承载能力进行评判。但荷载试验需封闭交通且耗资较大。

有限元建模计算具有速度快、成本低等优点，能有效地模拟实际结构的静力、动力、疲劳强度等特性。有限元建模在设计图纸阶段就可以实现，不一定需要实际结构。但是有限元计算仅仅基于设计图纸，与实际结构存在误差。有限元建模过程误差来源[3-5]主要包括：①模型阶次误差；②模型结构参数设置误差；③模型结构误差，如建模时采用一些简化假定等。试验过程的误差来源主要包括：①实验设备固有的系统误差；②测试条件带来的误差；③人为测试误差等。通常认为试验数据相对于有限元模型是更为可靠的，因此有限元模型修正主要依托试验数据来提高准确度和可靠度。

现阶段主要是通过结构的动力参数或静力参数来对结构有限元模型进行修正，而基于动力模型修正与基于静力模型修正各有利弊。为了得到更符合实际情况的有限元模型，以某BRT 为工程背景。首先进行动力模型修正。在基于动力的有限元模型修正中，考虑到结构自振频率对结构刚度的变化较为敏感，通过结构实测自振频率对有限元自振频率进行修正，进而得到能够反映结构整体信息和动力特性的有限元模型。在此基础上再进行基于静力模型的精细化修正。结构静力有限元模型精细化修正[6-7]是利用结构静力测试响应信息，通过调整参数的方法使结构静力响应的有限元计算值与实测值尽可能一致，从而使得修正后的结构有限元模型能兼顾到结构的局部特征，增大参数识别结果的有效性和可靠性。

1 基于动力的有限元模型修正

1.1 优化函数

为了使目标函数最优化，目标函数的构造主要是利用测试值与计算值的差值。在基于动力测试数据的有限元模型修正中，目标函数主要是通过测试和理论的固有频率、MAC、模态柔度等相关函数进行构造，采用的目标函数为[8-9]：

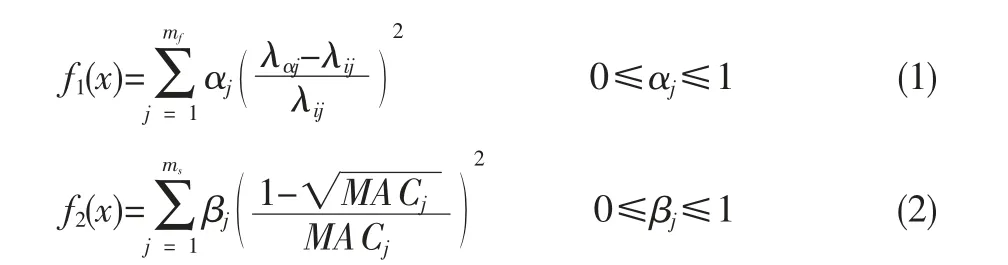
式中，f1(x)为基于频率的目标函数；f2(x)为基于MAC的目标函数；α 和β 为权重系数；λαj为j 阶理论特征圆频率；λtj为j 阶试验特征圆频率；MACj为第j 阶的模态保证准则值。

模态柔度矩阵被用于参数识别有不同的方式[10-11]，Bijaya Jaishi[12]通过式(3)和式(4)构造有限元模型修正的目标函数，式(3)称为一致荷载面，式(4)则是相应的目标函数：

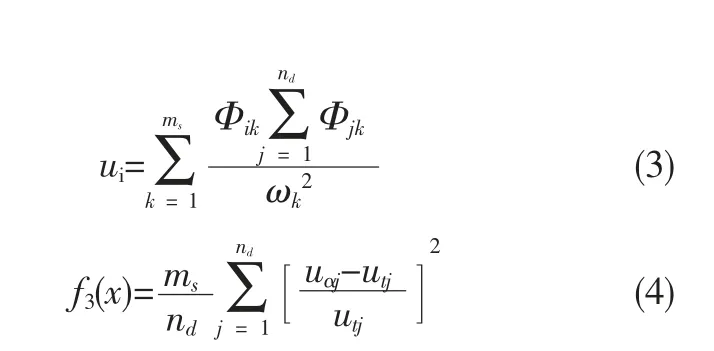
式中， f3(x)为基于模态柔度的目标函数；uαj为理论的一致荷载面；utj为试验的一致荷载面；ms为测试的自由度数；nd为测试的模态阶数；[Φik] 为质量归一的振型矩阵；ωk2(k=1，2，...，n)为固有频率。

将频率、MAC 和模态柔度三个目标函数联合起来，可以构造如下的目标函数，如式(5)所示，同时可以使用式(6)和式(7)的约束条件：

式中， f4(x) 为联合频率、MAC 和模态柔度的目标函数；UL 为理论和实测特征值误差的上限；L1为MAC 的下限；η1、η2、η3为权重系数，权重系数根据不同目标函数对结构灵敏度的不同进行分配。

1.2 有限元模型的建立

选取具有代表性的BRT 高架桥梁A 标段第24 联作为研究对象，应用桥梁有限元计算软件建立桥梁的三维有限元模型，验算桥梁设计是否满足城市道路B 级、直线电机B 型活载和实测BRT 车辆荷载的通行要求。该桥为4×30m 预应力钢筋混凝土等截面连续箱梁直桥结构。主梁采用单箱单室结构形式，模型采用梁单元模拟，截面按照真实截面建立，边界条件按实际边界条件模拟。桥梁纵向为X 轴，横向为Y 轴，竖向为Z 轴。有限元模型见图1。

图1 Midas civil 整体有限元模型

1.3 自振特性试验

(1)测点布置

将竖向加速度传感器按7.5m 间距布置在各跨上，测点布置详见图2。试验采样频率为100Hz，采样时间为10min。

图2 传感器测点纵桥向布置示意图(单位：cm)

(2)动力特性分析结果

理论与实测前四阶竖向频率见表1 所示。从表中可以看出，竖向一阶、竖向二阶、竖向三阶实测频率和理论频率有一定的误差，竖向四阶吻合度较高，说明建立的有限元仿真模型基本符合桥梁实际状况。为得到更精确的模型，还应进行修正。

表1 修正前计算和实测动力特性

1.4 基于动载试验的模型整体修正

本次修正采用将频率、MAC 和模态柔度分别作为目标函数及联合频率、MAC 和模态柔度的单目标函数f4(x)进行修正数值模型[13]，并对修正效果进行比较。有限元模型修正都是基于实测模态频率和振型。

选择混凝土的质量密度、弹性模量、桥面铺装厚度、支座的竖向弹簧刚度作为模型修正参数。参数灵敏度分析表明：混凝土的质量密度对各阶频率的变化具有几乎相同的影响，混凝土的弹性模量对各阶频率都具有较高的灵敏度，桥面铺装对各阶频率都有一定的影响，且影响不一致，支座的三向弹簧刚度对频率影响也不一致。

经过修正后模型的竖向频率与实测频率能够很好地吻合，MAC 值也提高了。表明修正后的模型更符合实际情况，修正后模型的动力特性和实测的结果见表2 所示。

表2 修正后计算和实测动力特性

从模型修正结果来看，修正后的模型更能符合实际情况，表明修正后的参数更接近桥梁的真实参数。从修正后的参数来看，混凝土弹性模量有所增加，表明实际混凝土弹性模量较设计要大，本桥使用的是盆式橡胶支座，弹簧刚度较大与桥梁实际情况较符合，结果见表3。

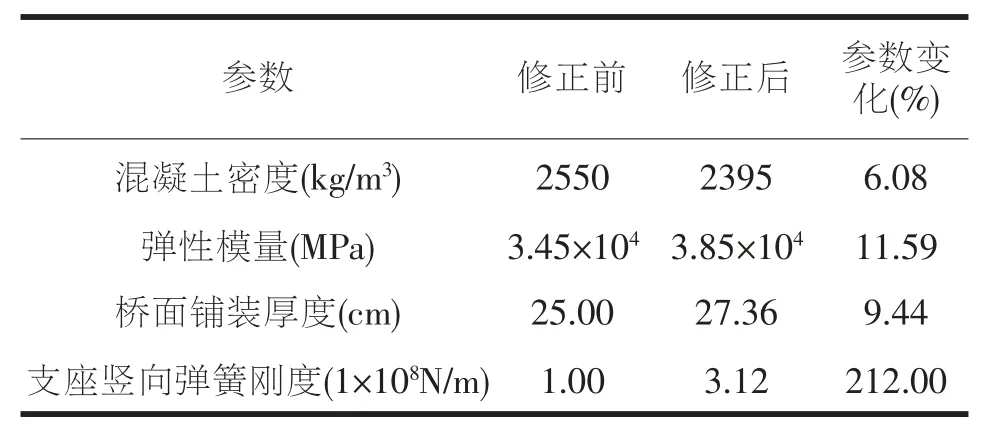
表3 动力参数修正表

基于动力的混凝土连续梁桥模型修正表明，采用联合频率、MAC 和模态柔度的目标函数进行修正后，模型的动力特性与实测的更为接近。经过修正后的模型理论频率、振型与实测值误差在3%之内，表明修正后的模型与实际桥梁更为吻合。

2 基于静力的模型精细化修正

2.1 基于单目标优化的有限元模型修正方法

结构静力有限元模型修正优化问题中，式(8)为待修正参数X 的约束状况，即X 的上、下限条件，决定了它的求解方法。

结构静力有限元修正优化问题的求解，在正常情况下，按无约束优化问题求解算法得到的待修正参数X*处于其合理取值范围内，即满足Xl≤X*≤Xu，这是最理想的情况。但是，在少数情况下，当结构初始有限元模型偏差过大、更多的是结构静力荷载试验误差过大时，按无约束优化问题求解算法得到的X*会超过其合理取值范围，得到的修正结果是没有意义的。此时希望在待修正参数X的合理取值范围内，尽可能得到其最佳解，此条件下，即为约束优化问题，应采用与其相关的求解算法。

所以，结构静力有限元修正优化问题求解算法的实现可以按以下方案进行：

先按无约束优化问题算法求解，若X*满足Xl≤X*≤Xu，则即为最优解；当X*超出其合理取值范围时，按约束优化问题算法求解。当然，也可直接按约束优化问题算法求解，但其复杂的算法实现过程在正常情况下是不必要的。

结构静力有限元修正无约束优化问题的标准数学模型为

结构静力有限元修正约束优化问题的标准数学模型为

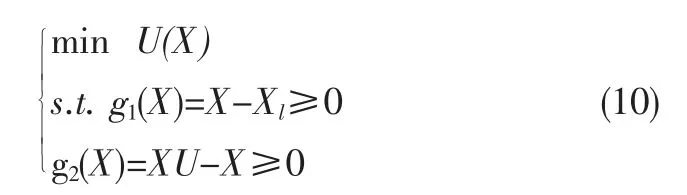
无约束优化问题的求解算法主要有梯度法、修正Newton、拟Newton 法、共轭梯度法、Powell 直接法等。约束优化问题的求解算法主要有序列二次规划法(Se-quential Quadratic Programming，SQP)、可行方向法、Lagrange-Newton 法等。其中，梯度法、拟Newton 法、序列二次规划法(SQP)由于计算中不直接使用目标函数的二阶微分，是结构静力有限元修正无约束和有约束优化问题的基本求解方法。

2.2 静载试验概况

(1)试验荷载概况

荷载试验分四个工况进行。荷载效率为1.00～1.05，满足规范要求，具体情况见表4。

(2)测点布置

①应变测点本次静载试验共布置4 个应变测试截面，8 个应变测点。应变测点布置及编号见图3 所示。

表4 各工况加载情况及测试内容汇总表

图3 应变测点平面布置示意图

图4 挠度测点平面布置示意图

②挠度测点

挠度测试采用水准仪测量，共布置9 个挠度测试断面，18 个挠度测点。挠度测点布置及编号见图4 所示。

3 基于静载试验模型精细化修正后理论结果与实测结果对比

(1)修正参数的选取

有限元模型待修正参数的选择，即结构有限元刚度矩阵的参数化，应符合以下几个基本原则：①所选参数应反应结构主要力学性能； ②静力实测响应应对所选参数具有较高灵敏度；③所选参数之间应彼此独立。

由于影响桥梁挠度、应变的主要因素为混凝土弹性模量，因此选择混凝土的弹性模量作为修正参数。从基于静力模型精细化修正的结果来看，修正后的模型比修正前更符合实际情况，参数修正后，弹性模量为3.68×104MPa。

(2)基于静力模型精细化修正后理论结果与实测结果的比较

①静力修正后的挠度比较结果

基于静力精细化修正后主桥挠度实测值与理论值结果见表5。可以看出挠度误差基本在15%以内，基本满足需求。

②静力修正后的应变比较结果

基于静力精细化修正后主桥应变实测值与理论值结果见表6。可以看出应变误差基本在15%以内，基本满足需求。

4 结论

(1)对厦门BRT 混凝土连续梁桥进行环境振动测试，获得该桥跨结构的基本动力参数如自振频率、阻尼比及固有振型，为有限元模型修正提供依据。采用模态频率作为目标变量，选取混凝土的质量密度、弹性模量、桥面铺装厚度、支座的弹簧刚度作为修正参数，竖向前4 阶自振频率作为响应特征，基于动力对该桥的初始有限元模型进行了模型修正。修正后有限元模型的计算频率与实测频率误差在3%以内，MAC 值在93%以上，吻合较好。