异结构分数阶复混沌系统的双混合函数投影同步

张晓青

(太原工业学院 理学系，太原 030008)

0 引言

混沌同步表示的是在特定条件下，两个或多个混沌系统的运动状态可以达到一致.由于混沌系统的内在随机性，以及它对初值的极度敏感依赖性，学者们一度认为达不到混沌同步.早在二十年前，著名科学家Pecora和 Carrol[1]在电路实验中实现了混沌同步，这一开创性成果推动了混沌同步理论的发展.随着学者们的深入探索，提出了多种同步概念，比如：反同步[2-3]，投影同步[4]，函数投影同步[5]，双同步[6-8]等.不同的同步概念表示着驱动、响应系统状态变量不同的对应关系.其中双同步是2000 年被Liu 和Davids[6]首次提出的一种特殊的同步现象，它表示着两个驱动系统和两个响应系统之间的同步.Othman等人[7]研究了参数未知的混沌以及超混沌系统的双同步以及参数辨识.Ning 等人[8]讨论了Lorenz系统和Rossler系统这两种不同的三维连续混沌系统的双同步问题，并且得到了两个不同混沌系统对偶同步的充分条件.双混合函数投影同步比一般的双同步更为复杂，实现起来难度更大，目前尚未见报道.复混沌系统出现在很多物理和工程领域，比如激光物理中，双能级原子组成的环形激光系统中的原子极化和电场振幅均是复数[9].复混沌系统还可以有效地应用于通信，通过将变量的数目增加一倍，从而增加传输内容以及提升安全性[10].但是目前关于复混沌系统的有关同步研究还不多见.王诗兵等人[11]利用Lyapunove理论设计了控制器，实现了超混沌复系统的广义组合同步.Yadav等人[12]研究了分数阶混沌系统的双函数投影同步，利用主动控制法设计了非线性控制器.本文首先描述了双混合函数投影同步的概念，其次基于追踪控制理论设计了普适的非线性控制器，然后分别将复Lorenz系统，复呂系统，复T系统、复Chen系统作为驱动、响应系统，实现了驱动响应系统的双混合函数投影同步.数值仿真结果表明了双混合函数同步的可能性和方法的有效性.

1 知识准备

驱动系统1:

dqXd/dtq=AXd+f(Xd)

(1)

此处Xd=Xd1+iXd2为复状态变量，则

(2)

驱动系统2:

dqYd/dtq=BYd+g(Yd)

(3)

此处Yd=Yd1+iYd2为复状态变量，则

(4)

其中A,B∈Rn×n,A1,B1∈Rm1×m1,A2,B2∈Rm2×m2,f,g为已知的非线性函数矩阵.

将驱动系统的状态向量进行线性组合得到如下的混合信号：

Vd=[a1,a2,…,am1]Xd1+[a1,a2,…,am2]Xd2+

[b1,b2,…,bm1]Yd1+[b1,b2,…,bm2]Yd2=

其中

响应系统1：

dqXs/dtq=CXs+h(Xs)+U(1)(t)

(5)

此处Xs=Xs1+iXs2为复状态变量，则

(6)

响应系统2:

dqYs/dtq=DYs+l(Ys)+U(2)(t)

(7)

此处Ys=Ys1+iYs2为复状态变量，则

(8)

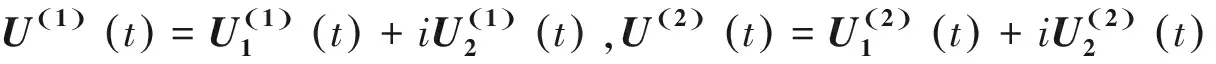
其中

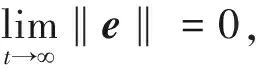
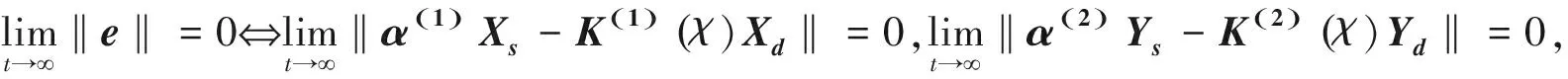
引理1[13]对于分数阶混沌系统：dqX/dtq=AX,X(0)=X0,q=(q1,q2,…qn)T,

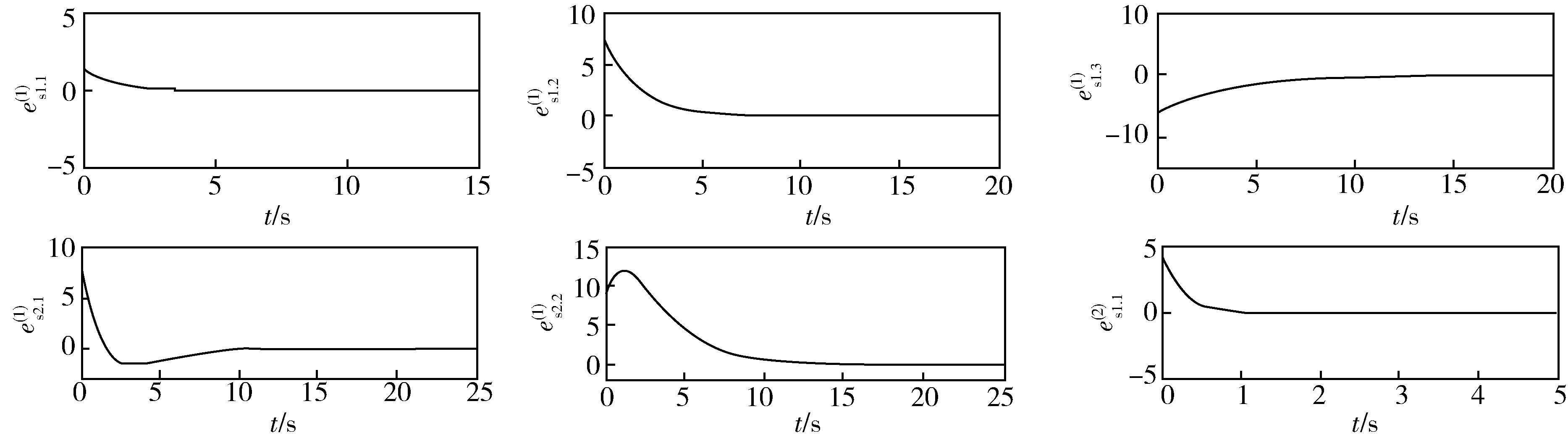
0

定理1根据追踪控制理论设计控制器如下：

(9)

(10)

把所设计的控制器(9)代入上式得，

(11)

因为

(12)

2 异结构分数阶复混沌系统的双混合函数投影同步

将分数阶复Lorenz混沌系统[14]作为驱动系统1，动力学模型为：

(13)

将分数阶复呂混沌系统[12]作为驱动系统2，动力学方程为：

(14)

将分数阶复T系统[12]作为响应系统1，动力学方程如下：

(15)

分数阶复Chen系统[15]作为响应系统2，动力学方程为：

(16)

分数阶复Lorenz系统、复呂系统、复T系统、复Chen系统的初值分别取为(1,3,5,2,4)，(2,5,9,3,6)，(-1,8,-1,9,-5)，(6,5,12,9,7),q=0.94时，各系统产生混沌吸引子.

根据定理1设计控制器.其中：

Xd1=(x11,x12,x13)T,Xd2=(x14,x15)T,

Yd1=(y11,y12,y13)T,Yd2=(y14,y15)T，

Xs1=(x21,x22,x23)T,Xs2=(x24,x25)T,

Ys1=(y21,y22,y23)T,Ys2=(y24,y25)T，

取

得误差系统为：

(17)

因为arg(λi(H))=π≥(q/2)π，0

α=(-2,4,1,6,3,1,-5,4,7,3),

时，误差系统见图1，从图可知，驱动系统与响应系统在很短的时间内就实现了双混合函数投影同步.

图1 系统(13)(14)和(15)(16)的双混合函数投影同步误差

3 结论

本文研究了异结构分数阶复值混沌系统的双混合函数投影同步，首次刻画了复值混沌系统的双混合函数投影同步概念，利用追踪控制法设计了普适控制器，然后实现了复Lorenz系统、复呂系统与复T系统、复Chen系统的双混合函投影同步.利用MATLAB数值仿真发现误差系统在短时间内趋于0，与理论分析相吻合，表明了所提方案的合理性.研究结果在激光物理，信息安全传输等方面具有潜在的应用价值.