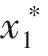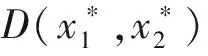关于出租车和网约车竞争系统的稳定性分析

张 雪,由 悦

(吉林师范大学 数学学院,吉林 长春 130000)

0 引言

在国民出行时,出租车是重要的交通工具之一,特别是在北、上、广等一线城市及各省省会等二线城市,一直以来,“打车难”是备受人们关注的社会性热点问题.随着互联网的飞速发展,国内多家互联网类型公司依靠移动网络信息的传递,研发了许多款线上打车软件,例如快车、滴滴打车等,推出了网约车服务,实现了司机与乘客之间的无距离沟通,大大节约了资源成本,减去了很多不必要的资源和人力浪费,同时节省了时间,减轻了当今社会“打车难”的问题.但是,由于线下出租车与线上网约车的消费群体基本相同,必将产生生存资源竞争,从而导致经济竞争的问题.为了达到商业利益最大化,研究出租车和网约车数量之间的关系是根本.我们利用两种群之间相互作用的基本的数学模型L-V模型来研究出租车和网约车之间的竞争关系,此模型是logistic模型的延伸,对生物数学的发展有着重要影响[1].用渐进稳定性定理[2]和全局渐进稳定[2]以及求全导数[3]对模型中的平衡点进行讨论,证明平衡点存在且唯一,由此观察两个群体之间相互竞争时的数量变化情况.

首先,为讨论提供理论依据,参考以下定理：

设平面自治系统

(1)

的解是x(t)=(x1(t),x2(t),…,xn(t))τ.

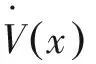
定理2如果(1)的零解是稳定的,又是吸引的,则称(1)的零解是渐进稳定的,假如(1)的零解的吸引域是整个Rn,则称(1)的零解是全局渐近稳定的.

1 模型分析

出租车市场归属于传统性的行业市场,公交车由于线路的确定性及每站每停的耗时性导致许多时候人们不会选择此交通方式,所以出租车在出行中占领主导地位.但即便如此,出行还是具有着极高的不确定性,特别在上下班高峰期,存在着许多叫不到车的现象.随着当今计算机行业技术的提高,互联网渗透到各行各业,无处不在,各种打车软件也开始崭露头角,逐渐改变我国国民的生活方式,也提高了国民的生活质量[5].与此同时,打车APP由于入行门槛低,促使网约车数量一味地增加,正常的出租车行业受到前所未有的冲击,出租车司机的利益受到威胁.所以,建立关于出租车与网约车竞争系统的数学模型并对此进行分析,维持出租车和网约车之间数量的稳定与平衡,实现出行市场经济的最大效益,使资源得到有效配置在当今社会中显得尤为关键[5].出租车和网约车在t时刻增长的同时,两者相互竞争所满足的数学模型[4]如下：

(2)

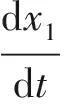
(3)

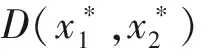
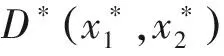
变换可以得到方程组

在变形可以得到方程组Ⅰ，Ⅱ

Ⅰ

Ⅱ

将模型(2)化为

(4)

选取函数

其中,a1>0,a2>0且a1，a2均为常数.即函数V(x1,x2)也可以表示为

经计算得,

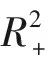
计算V(x1,x2)的全导数可得

(5)

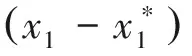
当

δ=(a1q1+a2p2)2-4a1a2p1q2<0

(6)

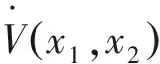
δ=(a1q1-a2p2)2-4a1a2(p1q2-p2q1)<0

(7)

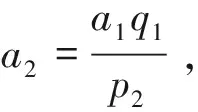
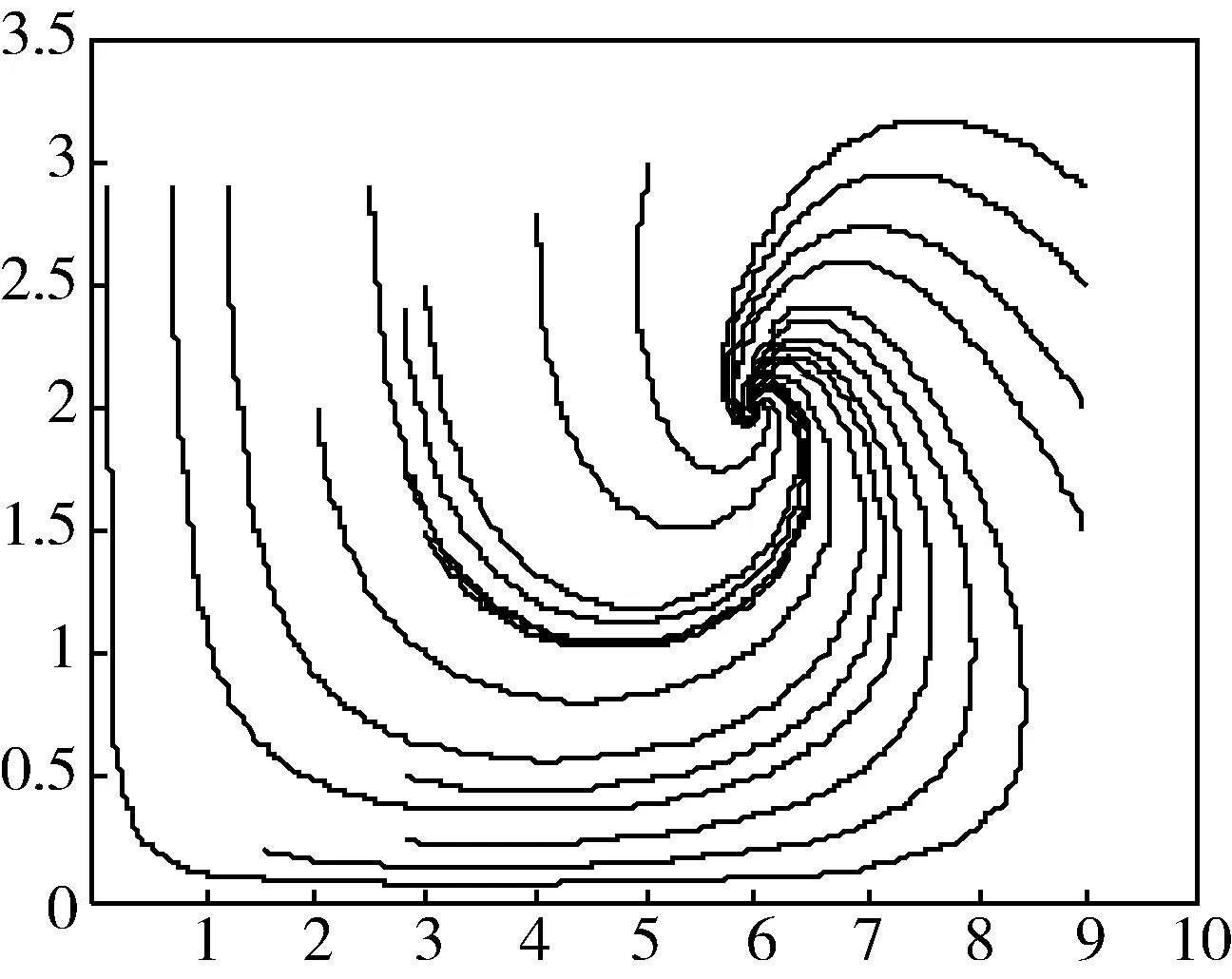
图1 出租车和网约车的数量变化情况

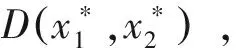
2 系统主要结果的生物学意义