基于改进预处理算法的复杂网络构建与分析❋
2020-01-07李腾跃
郑 旭,冯 晨,李腾跃,程 伦,何 波
(中国海洋大学信息科学与工程学院水下机器人实验室,山东 青岛 266100)
海洋资源的开发及全球自然环境保护的需要,极大程度推动了人们对于自主式水下机器人(Autonomous Underwater Vehicle,AUV)的研究[1-2]。AUV自身结构复杂,系统的非线性与不确定性强,所处的海洋环境变化莫测[3],这些因素会对AUV状态监测数据产生很大的干扰,因此,对AUV数据的波动模式进行准确描述有较大的难度,国内外的相关研究也一直在不断地进行[4-7]。
近年来,复杂系统分析方法—复杂网络,被广泛地应用于复杂系统研究中,基于复杂网络的非线性时间序列特征的挖掘是其中一个重要的研究方向[8-11]。这是因为,复杂网络在刻画整体波动情况的同时,也可以对时间片段的波动模式进行精确的描述,有助于更清晰地了解时间序列的波动模式及规律。但实际监测数据中往往包含许多噪声,直接使用原始时间序列构建网络会对分析结果产生很大干扰[12-13],因此,需要对数据进行预处理,才能使构建出的复杂网络中的节点更加准确、有效的描述时间序列中关键的波动模式。
近年来,随着国内外学者对时间序列预处理研究的深入,涌现了许多的优秀算法[14-15]。分段累积近似算法(PAA)[16]成为一种常用的数据预处理方法,在此基础上,Eammon又提出了符号化的相似性度量(SAX)方法[17]。该方法可以在一定程度上去除干扰,并以符号化的方式表明时间序列的大小特性,但缺乏对于序列模式之间转化的描述,且需要数据服从高斯分布,不具有普适性。另外PAA算法在去除噪声的同时也平滑掉了一些关键的峰值点,会使整体的波动模式发生变化,对分析结果产生不利影响。定性趋势分析方法(Qualitative Trend Analysis,QTA)[18-19]被用于时间序列的描述中,该方法可以用符号化的方式准确表现出时间序列的波动模式,但无法排除冗杂波动的干扰,会产生许多不必要的波动模式。因此,需要探寻到一种新的时间序列预处理算法,既可以保留关键的峰值信息,又可以去除冗杂波动的干扰,并能适用大多数的数据。
针对AUV这类复杂的非线性系统的航行状态描述问题,本文构建AUV航行监测时间序列复杂网络,分析AUV时间序列波动模式。在构建复杂网络过程中,针对实际数据中噪声干扰严重的问题,本文使用改进的预处理方法去除噪声干扰,能够优化复杂网络构建,使复杂网络更加准确地描述AUV系统状态。
1 预处理算法与复杂网络构建方法
1.1 改进的预处理算法(Pro-DPCA)
为更好的实现数据的预处理,既保留关键的转折点,又能去除多余的波动,本文提出了一种改进的数据预处理算法,算法分为映射、聚类、复原三步。首先,将长时间序列看作若干个长度为3的短序列,根据映射规则将短序列投影到二维平面内,用二维平面的坐标表示段时间序列的波动模式。然后,利用密度峰值聚类算法对平面内的点进行聚类,聚类以后,波动模式相似的点会被分到同一类。最后,根据复原函数重新将二维平面的点转化为时间序列。
1.1.1 映射 设需要处理长度为n的时间序列{f1,f2,…,fn},将其划分为多个长度为3的段时间序列fi-1,fi,fi+1(若长度n不是3的倍数,可以适当增加或减少以一个数据点,一般来说n远大于3)。映射后的参数作为二维平面的横纵坐标X,Y,每个短时间序列映射到二维平面的结果如图1所示。

图1 映射过程示意图Fig.1 Mapping process diagram
选取映射参数:将映射后的横坐标定义为中间点到首尾两点连线的距离,纵坐标为首尾两点的高度差。具体公式如下,式中xi,yi分别表示第i个数据点fi的横纵坐标值。
Xi=
i=2,…,n-1;
(1)
Yi=yi+1-yi-1,i=2,…,n-1。
(2)
这样选取映射参数的优势如下:
(1)两个参数之间不存在直接的相关性。
(2)两个参数的取值范围相同。
(3)两个参数的变化可以完备的表现出3个数据点的所有变化形式。
(4)对于增大、保持、减小等不同模式的变化敏感,且映射后相反模式之间的距离最大。
1.1.2 密度峰值聚类(DPCA) 聚类采用Alex Rodriguez和Alessandro Laio提出的基于密度峰值的聚类方法[20]。其主要思想是寻找被低密度区域分离的高密度区域。对于一个数据集,聚类中心被一些低局部密度的数据点包围,而且这些低局部密度的点距离其他有高局部密度的点的距离都比较大[21]。在这样的模型中,DPCA主要有两个需要计算的量:第一,局部密度ρi;第二,与高密度点之间的距离δi。局部密度ρi的定义为:
ρi=∑jχ(dij-dc)。
(3)
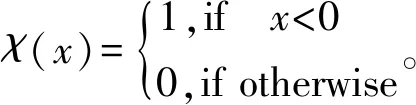
距离δi的定义为:
(4)
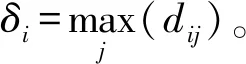
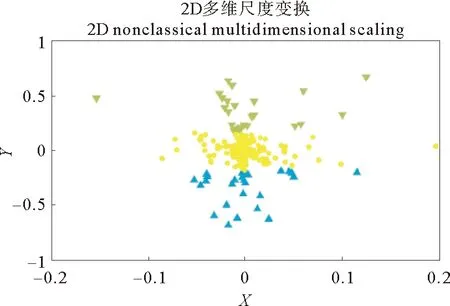
图2 样本聚类结果Fig.2 Sample of clustering results
1.1.3 复原 在第一步中,原始时间序列被转化成了诸多长度为3的片段,并将它们映射到二维平面中,现在需要将其复原,也就是根据聚类的结果把它们从二维平面转化为时间序列,复原公式如下:
(5)
式中Z表示复原后的序列,若第一个点被分为class1,那么Z1,2,3=f1。
图3展示了不同算法对含噪声时间序列的预处理结果。通过对比可以看到,本文提出的算法不仅保留了关键的峰值点,而且成功的消除了无关波动的影响,保留了数据关键的波动模式。这是因为虽然映射后的结果与基元表示法[22]都能完备的表现所有波动模式,但经过聚类以后,一部分波动模式会根据其波动幅度大小以及形状的不同,更加靠近数据主要的波动模式(如上升、下降、保持等),从而达到消除冗杂波动的目的。而部分符号化的复原方式则很好的避免了在PAA算法中,处理后的数据无法保留原数据的关键峰值,仍有很多冗杂波动。另外,PAA算法预处理后的数据并不符合高斯分布,因此无法直接使用SAX算法进行后续处理。
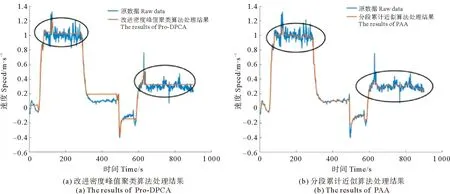
图3 不同预处理算法的结果Fig.3 The results of different pretreatment algorithm
1.2 复杂网络构建
对于一个时间序列f1,……,fn,将时间序列中两相邻点的增大符号表示为H,不变符号表示为M,较小符号表示为L[23]。
(6)
然后定义滑动窗口n,滑窗内n个符号构成的短模式组作为网络的节点,模式组之间的转换构成网络的连边,连边的权重ω即为两个模式组之间转化的次数,构建有向加权复杂网络,表1显示了复杂网络的构建流程,滑窗的选取有所重叠,一定程度上包含了前一片段的信息,使得片段之间具有记忆性和传导性同时不缺乏多样性[24]。

表1 情况下的复杂网络构建流程Table 1 The process of complex networks building when n=3
2 Lorenz系统的实验与分析
2.1 Lorenz映射系统
Lorenz映射系统是最早发现的混沌运动的耗散系统,许多学者对它也进行了去噪方面的研究[25]。Lorenz系统方程表示见公式7,当ρ>24.74时,系统呈现非周期的混沌态。使用该系统产生的时间序列,验证本文方法的有效性和先进性。
(7)
2.2 数据与网络构建
选取参数为δ=18,ρ=28,β=8/3的Lorenz系统中连续1000个x值进行分析。首先使用本文提出的预处理算法对数据进行预处理,结果见图4,然后使用1.2节中的方法进行复杂网络的构建,结果见图5。
对网络结构进行分析可知,原始数据的网络(见图5(a))主要集中在上升下降两种模态,且节点转换模式主要集中在这两种模态的自转换中。而使用本文方法构建的网络(见图5(b))在结构上与原始数据类似,但出现了一种新的模态“MMM”。从时间序列的角度来看,它表示的是原始数据中上升或下降幅度较小的部分,即系统的平衡点附近;从曲线运动的角度来看,这一模态反应的是曲线围绕吸引子进行圆周运动时方向改变的部分以及即将转入另一吸引子的部分(见图6)[26]。因此本文算法构建的网络在准确描述数据的波动模式的基础上,对于Lorenz映射系统的物理意义也有着更深入的挖掘。
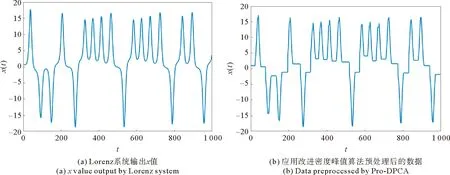
图4 Lorenz系统输出x值及其预处理后的数据Fig.4 x value output by Lorenz system and data preprocessed by Pro-DCPA

(其中节点大小代表节点强度高低,连线深浅代表权值大小。The higher the strength and weight ,the larger the node and the deeper the line in the net.)图5 复杂网络拓扑图Fig.5 The topological of complex network
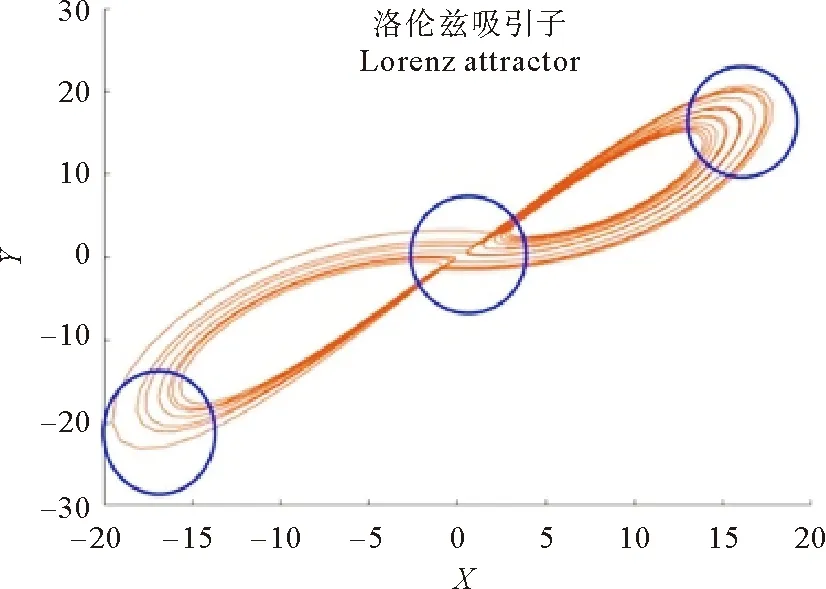
图6 lorenz系统XOY平面图Fig.6 XOY plane of the Lorentz chaos system
2.3 噪声对网络的影响
对原始数据添加信噪比为8 dB的高斯白噪声(见图7)进行实验,分析噪声对不同网络结构产生的影响,从而验证本文算法构建的网络对噪声的鲁棒性。
对于原始数据构建的网络,加入噪声后,网络的节点数明显增多,而且多个连边的权值较高(见图8(a)),对网络结构造成了较大影响。而用本文方法构建的网络加入噪声后(见图8(b)),虽然模态有所增加,但其连边权值明显很低,网络仍保持原有的结构。
使用节点自转换概率为指标,定量说明网络的稳定性。节点的转换概率,即节点i转换为节点j的概率,定义为prij:
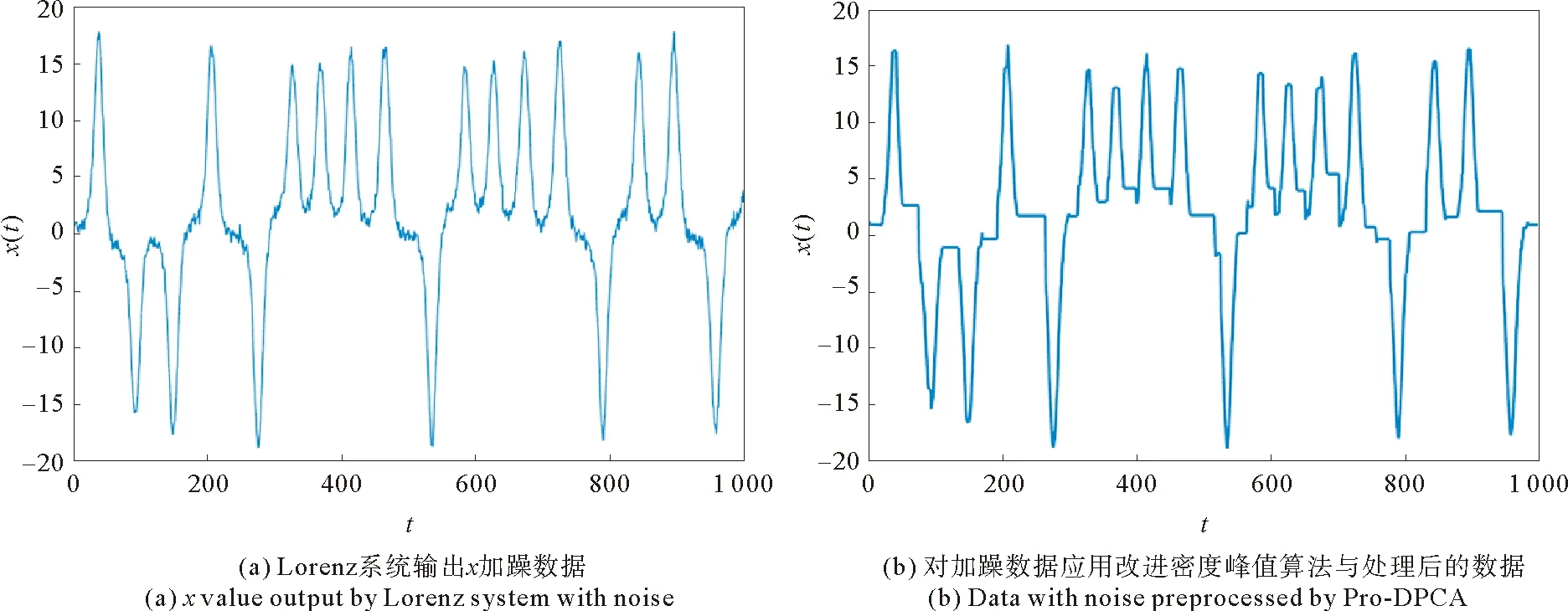
图7 Lorenz系统输出x加噪数据及其预处理后的数据Fig.7 x value output by Lorenz system with noise and data preprocessed by Pro-DCPA
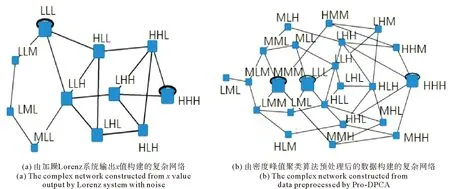
图8 复杂网络Fig.8 Complex networks
(8)
式中:ωij为节点i转换到j的权重;nsi表示节点i的强度。当i=j时,该式表达的则是节点的自转换概率。表2为使用不同预处理算法构建网络中关键节点的自转换概率。可以看出,对于未加噪数据来说,本文算法构建的网络与使用原始数据构建的网络差异不明显,但加入噪声以后,随着滑窗长度n的增加,原始数据构建的网络中,关键节点自转换概率明显下降,但使用本文算法构建的网络仍旧保持较高的自转换概率,特别是在n=10的时候,相较原始数据提升了15%以上。
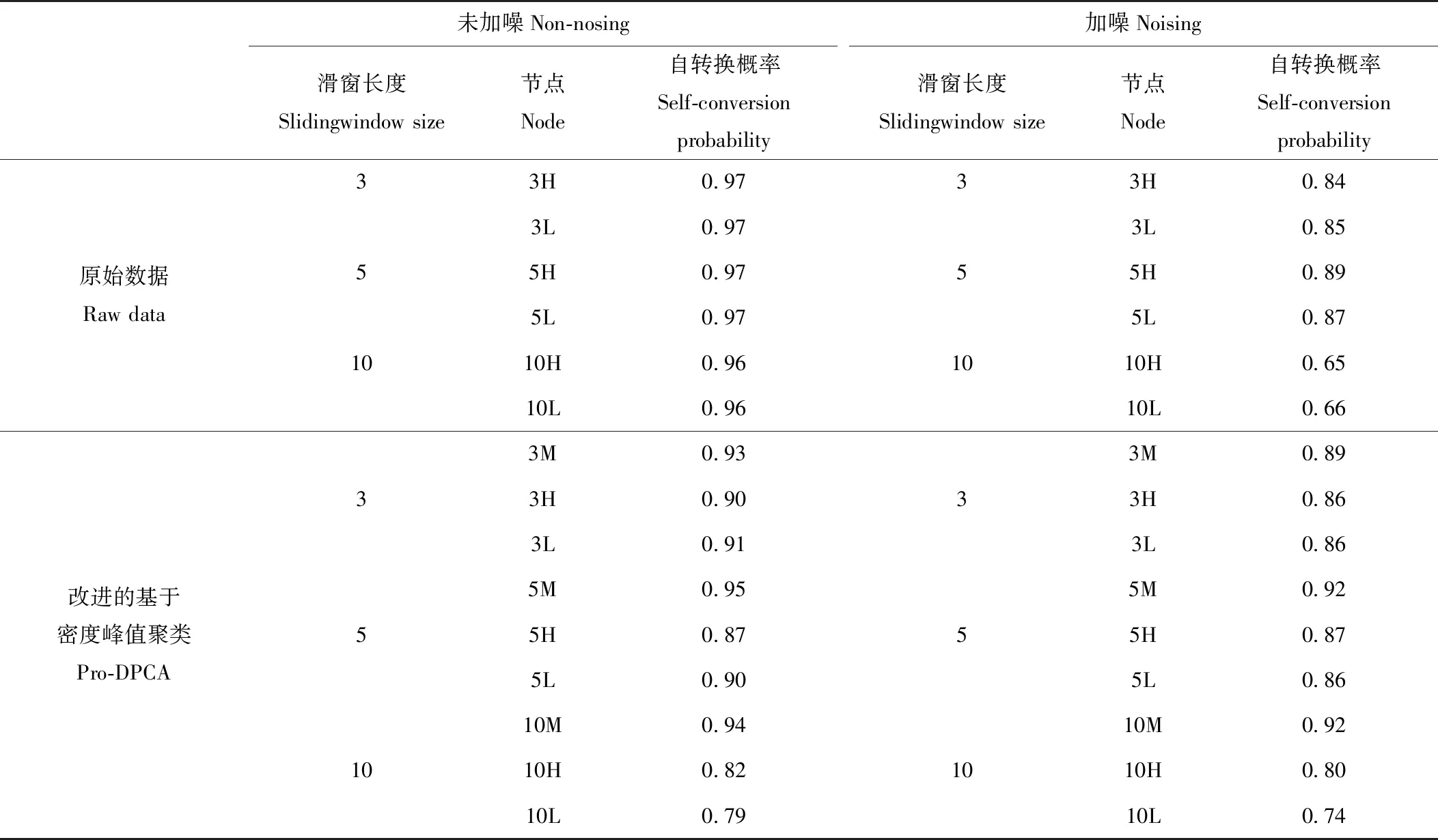
表2 网络关键节点自转换概率Table 2 The transition probabilities of the major node in the different net
注:表中3H表示3个连续H构成的节点。Here “3H” means the node “HHH”.
综上,通过Lorenz系统的实验与分析表明,使用本文算法构建的网络,不仅可以更加准确地表现系统的波动模式,还可以挖掘出更深的物理意义,而且对尺度和噪声都具有更强的鲁棒性。
3 AUV数据波动模式分析
3.1 数据获取及网络构建
研究选取AUV下潜状态下的实际速度数据进行实验,采样频率为1 Hz,如图9所示,实验选取深度增加部分的速度数据。然后使用本文提出的方法构建有向加权网络(见图10)。网络中节点表示了数据的波动情况,从理论上来说,通过不同模式的组合,共有33=27种可能的模式组出现,然而实际只出现了其中20种,使用原始数据构建的网络会有更多的模式出现,但更多的模式往往是因为一些无关的波动所引起。
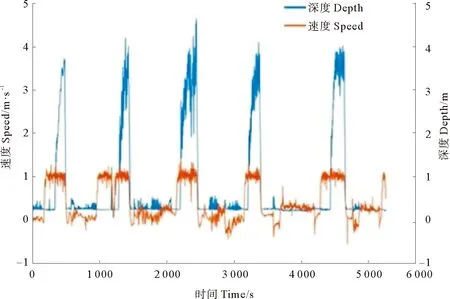
图9 AUV实际深度与速度Fig.9 The actual speed and depth of AUV
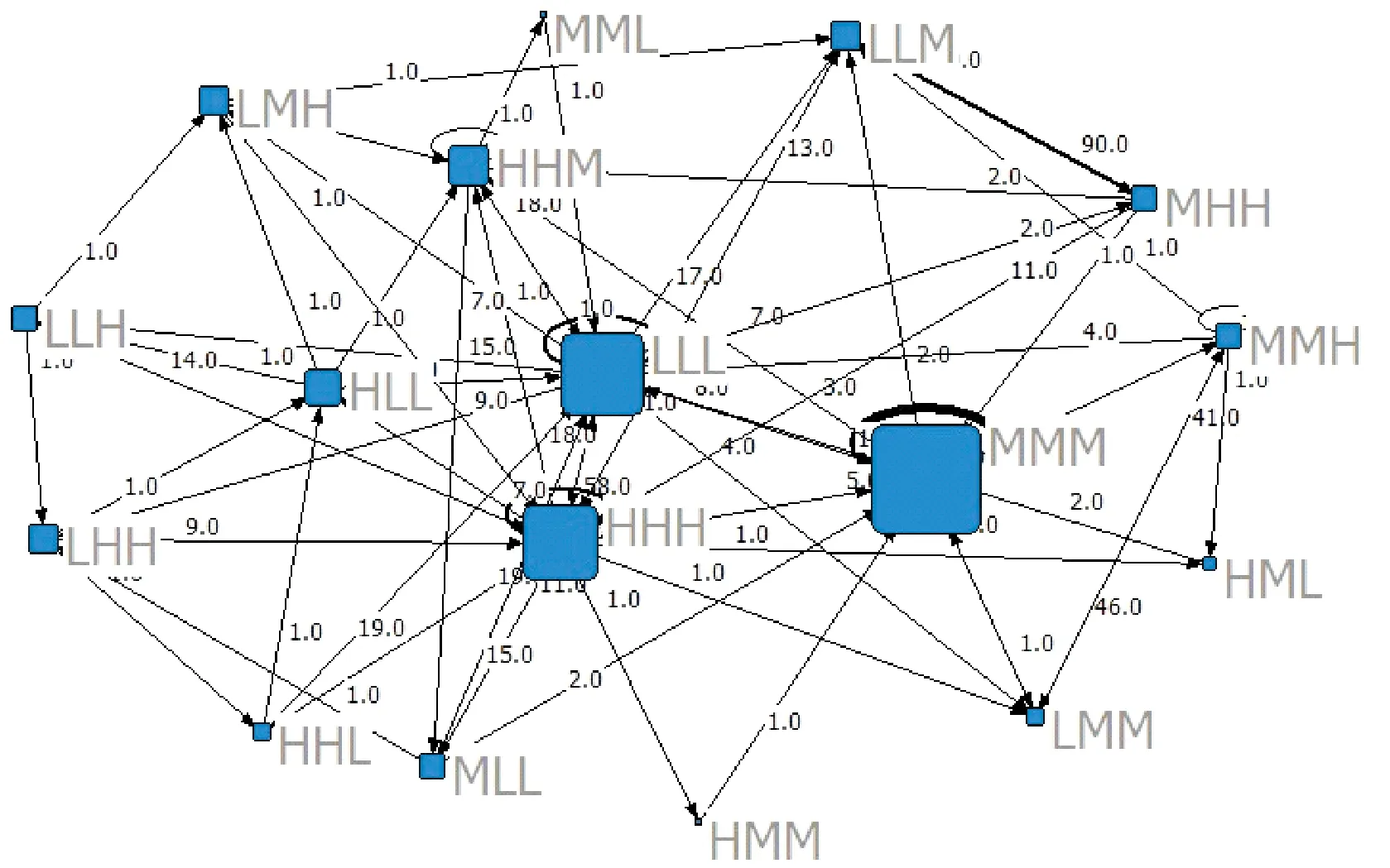
图10 AUV下潜阶段实际速度数据构建的网络(滑窗长度n=3)Fig.10 The topological of complex network based on actual speed during AUV submergence stage(sliding window n=3)
3.2 网络特性分析
基于构建好的网络,利用节点分布的统计学特性对网络进行分析,挖掘数据中的关键信息,掌握AUV的运动状态。首先观察每个模式所占的比例,了解数据整体结构。图11显示了网络中各模式的占比,其中M模式所占比例最高,这表明多数数据处于“保持”状态,AUV运行状态相对平稳。

图11 各模式所占比例Fig.11 The proportion of fluctuating models
接下来以节点为单位,使用节点强度nsi对网络进行分析,节点强度不仅考虑了节点的的相邻个数,同时也考虑了与相邻节点的权重
nsi=∑j∈Nωij。
(9)
式中:nsi为第i个节点的强度;ωij表示节点i和j之间的权重。
表3显示了使用Pro-DPCA算法构建的复杂网络中,强度前5的节点占比情况。其中“MMM”占了最大的比例66.3%,远高于其他节点。从图12可以看出,节点强度服从幂律分布,并呈现长尾特性,这表明主要波动模式集中在少数模态中,其他模态只占了很小的比例,对于该时间序列则主要集中在“保持”这一模态。这反映出AUV在下潜过程中基本保持匀速行驶,与实际情况相符合。

表3 节点强度及所占比例(n=3,Pro-DPCA算法)Talbe 3 Proportion of node strength(n=3,Pro-DPCA)
接下来选择不同的滑窗长度n,并使用不同的预处理算法进行网络构建,进行对比实验,观察Pro-DPCA算法与其他预处理算法以及原始数据所构成网络之间的差异,分析网络在不同尺度下是否依然可以准确表现数据的波动模式。
表4列举了3种算法在不同滑窗长度n下的关键节点占比情况,其中PAA算法选取的片段长度为3,因此节点数为原始的1/3。通过对比可以看出,使用本文算法构建的复杂网络可以准确的挖掘出数据中的大量“保持”状态,原始数据由于波动较多,很难表示出数据应有的波动模式,而PAA算法虽然对波动进行了平滑,但效果仍不理想。其中在n=3的时候PAA算法构成的网络达到了27个节点,表现了所有可能的波动模式,这也就意味着滑窗长度n=3这个尺度对于片段长度为3的PAA算法处于一个饱和的状态,进一步增加片段长度会使该算法在这里有更好的表现,但是这样也平滑掉了更多的关键峰值,而且会将序列维度进一步降低,对于其他的分析起到不利的作用[27]。另一方面,随着滑窗长度n的增加,PAA算法中的关键节点占比下降迅速,当n=10的时候不足1%,而使用本文算法构建的网络仍能有60%的比例,可以更好的适应滑窗尺度的变化。
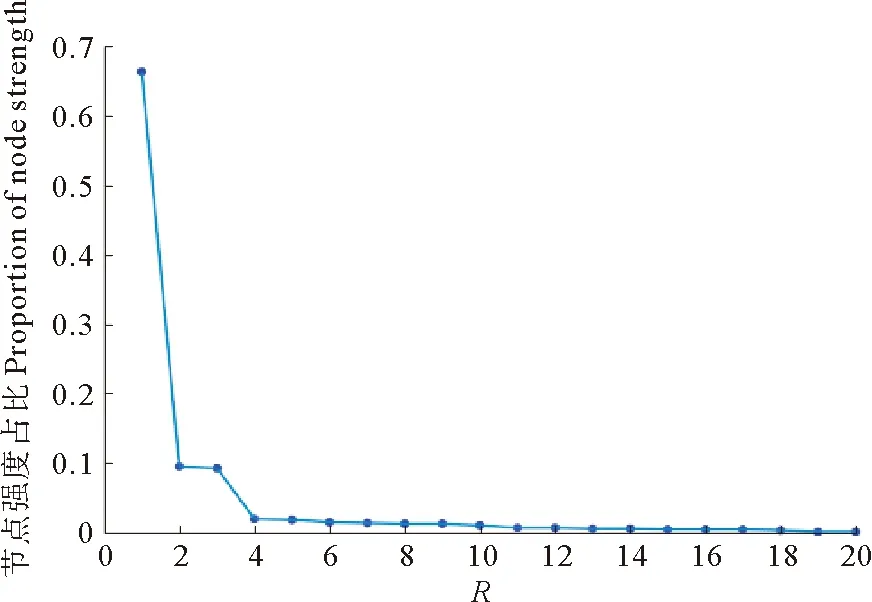
(其中R为节点按强度大小排序的秩。HereRis the serial numbers that are sorted by their node strength value.)
图12 节点强度分布
Fig.12 The distribution of node strength

表4 关键节点占比Table 4 The proportion of node strength in different net
注:表其中节点强度指的是网络中关键节点(连续n个”M”)的强度。The node strength is refer to the strength of the major node(ntimes of “M” continuity).
综上,通过实验和分析表明,本文提出的方法可以在含有大量冗杂波动的AUV数据中挖掘出主要的波动模式,准确表现出AUV的航行状态,并且对于尺度的变化有着更强的鲁棒性。
实际上,不仅限于AUV,在现实生活中的很多领域,例如风场信号、通信信号、工业中的滚动轴承信号等等,这些信号的时间序列也都是可以使用复杂网络方法分析系统状态的。而这些实际数据中往往也伴都随着噪声的干扰,本文的算法同样适用于这些领域。因此,本文提出的算法应用不仅局限于AUV数据的去噪,还有着其他更为广泛的实际应用。
4 结语
本文使用复杂网络的方法描述复杂非线性系统的状态,并提出了一种映射与密度峰值聚类结合的改进预处理算法,以此优化复杂网络的构建。在实验中使用Lorenz系统和AUV实际航行数据对本文方法进行了验证。结果表明,与传统方法相比,本文的方法可以更为准确地描述时间序列的波动情况,深入挖掘数据中的关键信息,且对噪声干扰和尺度变化具有更强的鲁棒性。本文的研究为去除时间序列数据中的噪声干扰这一问题提供了新的可行方案,在数据挖掘和复杂系统建模等领域有十分广泛的应用前景。
