阻燃钛合金摩擦着火热源模型及仿真分析

梁贤烨，弭光宝，李培杰，曹京霞，黄 旭

(1.中国航发北京航空材料研究院，北京 100095)(2.清华大学新材料国际研发中心，北京 100084)(3.北京市石墨烯及应用工程技术研究中心，北京 100095)

0 引 言

钛合金因具有比强度高、热强性好等显著优点,在现代航空发动机中得到广泛应用[1-4]。与此同时，由于钛合金导热性较差、燃点低于熔点，在发生异常摩擦时容易引起失去控制的燃烧,即发生钛火。鉴于航空发动机钛火的巨大危害性， F119等发动机大量选用了Ti-V-Cr系阻燃钛合金Alloy C (Ti-35V-15Cr)；EJ200发动机高压压气机叶片与机匣应用了防钛火涂层技术。

随着我国航空发动机技术的快速发展，对阻燃钛合金及防钛火涂层技术提出了更高的要求，阻燃性能评价、机理及应用等问题引起了高度关注。近年来，国内基于摩擦生热原理和着火热理论，建立了钛合金(含钛铝金属间化合物)燃烧试验技术、装置和评价标准《钛合金抗摩擦点燃性能试验方法》，并开展了试验研究和理论分析[5-7]。在摩擦着火过程中，转子与静子试件温度场的分布以及高温区域的温度场是计算着火温度、延迟时间等阻燃性能参数的关键。在实际摩擦着火设备进行试验过程中，由于存在高温以及振动等影响，同时试验时间较短(5～10 s)，很难对接触表面的应力、温度等参数进行准确地测量，且采用实验手段获取磨损数据费用较高，同时现有设备无法对发动机工况下的某些高温高压环境进行模拟，因此需要对着火过程进行理论建模及仿真分析，通过数值模拟结果对阻燃性能进行预测。

在摩擦着火试验过程中，转子试件会发生严重磨损，因此在理论建模时应充分考虑磨损的影响。目前，关于热-力-磨损耦合的仿真计算在搅拌摩擦焊、制动器等领域有较多的应用[8-15]。因此，本研究在现有试验基础上，采用热-力-磨损耦合的有限元模型结合FLUENT中动网格技术，对静子与转子试件摩擦着火过程的热源进行理论模型计算与分析。

1 理论模型

图1为静子与转子试件摩擦着火原理示意图[6]。摩擦着火试验过程中，转子与静子试件之间发生紧密接触。楔形转子试件高速转动过程中，在接触面上存在剧烈摩擦并在摩擦作用下产生高温热源。这些热量使试件材料温度升高，当温度达到钛合金着火温度时，发生燃烧。转子与静子试件热量传递的方式有表面对流、试件内部的热传导以及表面辐射等。热源模型考虑了转子与静子试件接触面的摩擦热源变化、转子试件的变截面磨损、试件内部的热传导和表面的散热等因素。

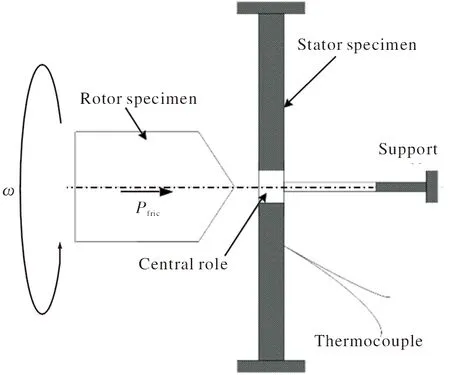
图1 静子与转子试件摩擦着火原理示意图Fig.1 Schematic diagram of friction ignition apparatus of stator and rotor specimens

建立热源模型时进行以下假设:氧气射流速度为定值；忽略材料的弹性变形；转子与静子试件的摩擦为滑动摩擦以及黏着摩擦结合的复合摩擦状态；忽略试件夹具的散热。接触面的热流密度q由摩擦力τ做功生成，按照公式(1)计算:

dq=ωrτrdθdr

(1)

式中:r为节点转动半径；ω为单位角速度；τ为摩擦力；θ为转动角度。

热源中的摩擦模型采用库伦模型，假定转子表面与工件之间为刚性接触，按照公式(2)进行摩擦力的计算。

τ=μP

(2)

式中:μ为摩擦系数，P为接触正应力。

在高转速条件下，磨损率ν是关于摩擦力和转速的函数，按照公式(3)计算。

ν=C(μPV)2

(3)

式中:C为磨损常数;V为线速度。

摩擦模型中，每级的磨损深度、磨损初始时间由方程组(4)确定。

(4)

式中:kw为磨损率;Ai为接触面积;ti为每级的磨损时间;hi为每级的磨损深度;T为试验总时间;H为磨损总深度;Pi为每级的接触正应力;F为接触面总压力。试验测定T、H和F，代入方程组中求解每级的未知参量，再将这些参量代入磨损子程序以及热源子程序中进行温度场的有限元模拟计算。

传热模型中，热量首先产生于接触面区域，随后在温度梯度的作用下向低温区传递。热传递的速度取决于材料的导热系数。通常来说，导热系数随温度变化而变化。温度越高，导热系数也越高。然而，相对于温度的变化，导热系数的起伏并不大，在一些研究中，为简化模型，也常对工件材料的导热系数取定值。传热模型采用傅里叶传热定律，按照公式(5)计算。

(5)

式中:k为热导率;ρ为密度；c为比热容;qinΩ为产热项。

除了材料内部的传热外，还有试件表面与空气的对流换热。对流换热是指固体表面与其周围流体间由于温差而引起的热量交换。对流换热实质上是热传导和热对流共同作用的结果，当流体流经固体表面时，通过固体表面的热流会在流体内部质点的作用下向流体扩散，即发生了固体表面与流体间的热传导。同时，流体内部质点的相对运动也会导致热量在流体中扩散，从而产生热对流。对流换热可用牛顿冷却公式(6)描述:

(6)

式中:n为空间矢量;h为对流换热系数;T和T0分别为固体表面及其周围流体的温度。

此外，试件表面还通过热辐射进行散热，试件温度越高，单位时间内辐射的热量越多。在摩擦过程中，因热辐射而损失的热量可通过简化的斯蒂芬-波尔兹曼公式(7)来计算。

(7)

式中:ε为辐射率或吸收率;σ为波尔兹曼常数。

2 有限元模型

采用FLUENT软件进行有限元模型的建立。考虑到实际摩擦着火过程转子的磨损，对转子试件模型进行等效建模，并将转子离散为7个部分，如图2所示。通过FLUENT软件中的动网格模块进行磨损子程序编程。转子与静子试件几何模型分为3部分:第一部分为转子试件区域；第二部分为静子试件区域；第三部分为转子与静子试件摩擦接触区域。有限元模型采用六面体网格划分，使用瞬态求解器进行求解，单位时间步长为0.08 s。静子试件中心孔处的圆形区域(直径约25 mm)采用O型块结构网格划分，如图3所示。

图2 转子试件有限元模型Fig.2 Finite element model of rotor specimen

图3 转子与静子试件的有限元网格Fig.3 Mesh of rotor and stator specimens

模型的边界条件分为磨损部分和热源部分，采用动网格的layering模式进行磨损仿真，网格容差设置为0.001 mm。由于FLUENT软件中没有接触应力模块，因此摩擦力以及热物性参数需要通过自定义函数预先施加。图4为计算流程图。转子试件不同级之间的交界面处采用热耦合形式，静子与转子试件接触面采用自定义热源。

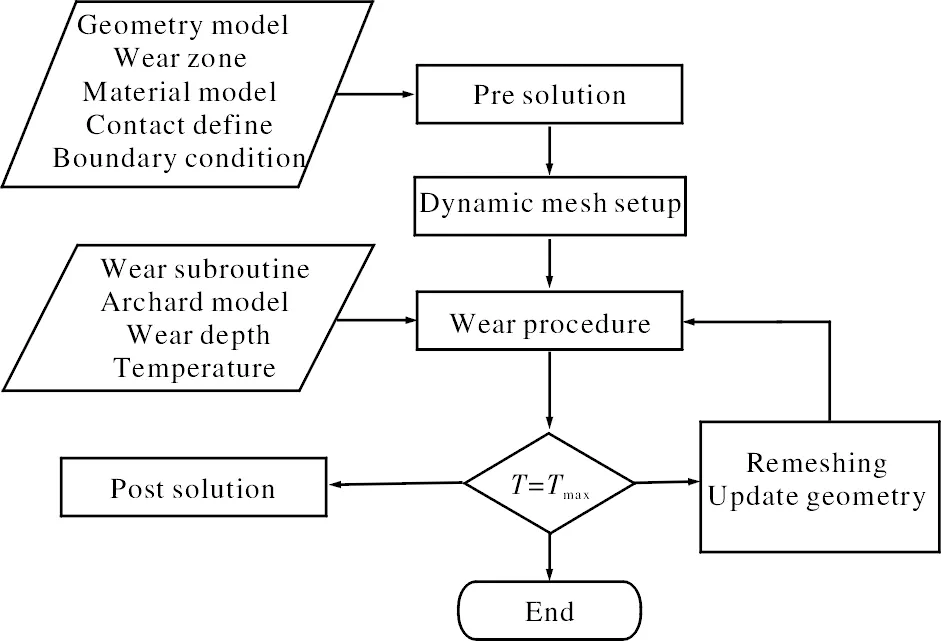
图4 数值计算流程图Fig.4 Flow chart of simulation

有限元模型边界条件具体参数给定如下:①采用550 ℃阻燃钛合金(Ti-35V-15Cr-0.3Si-0.1C, TF550)进行仿真，其热物性参数及摩擦系数通过试验获得[16]，在数值建模过程中假设温度高于973 K的热物性参数及摩擦系数的数值与973 K时的参数值近似相等；②转子与静子试件接触压力分别取200、400、700、900 N，环境温度分别取室温、673、823、1 273、1 773 K；③转子每级的磨损率、接触时间由方程组(4)确定，并通过UDF函数(用户自定义函数)预先加载于每级的接触面上；④转子试件转速为 5 000 r/min，静子试件中心孔半径为1 mm,转子试件初始接触面积为5 mm×2 mm，静子试件尺寸为 125 mm×27 mm×2 mm，转子试件尺寸为30 mm×27 mm×2 mm，转子夹角为120°。

3 结果与分析

图5为有限元模拟的200 N摩擦接触压力下TF550钛合金静子、转子以及静子背面的最高温度变化曲线。图6和图7分别为有限元模拟的静子试件背面和摩擦接触面的温度场。转子试件在200 N摩擦接触压力和初始室温边界条件下，初始接触0.5 s内(第一级转子与静子接触)，由于接触面积小，应力高，因此升温速率非常快；在0.8 s时，前两级转子和静子试件接触，接触面的温度在热累积的作用下达到了781.8 K，如图7a所示，而静子试件背面温度只有571.1 K，如图6a所示，最高温度出现在小孔周围区域；在2.4 s时，前四级转子和静子试件接触，静子接触面最高温度达到了1 000 K以上，如图7b所示，而此时由于磨损的原因，转子最高温度在900 K左右，同时，静子背面最高温度已经超越了转子试件最高温度达到了970 K，如图6b所示；在4 s时，静子接触面最高温度达到了1 400 K，而转子试件升温缓慢，最高温度仍维持在1 000 K以下，静子背面最高温度与静子接触面温度只有100 K左右的温差，如图6c及图7c所示；直到7.2 s时，背面温度约为1 900 K，达到了钛合金在空气下的燃点，如图6f所示，而此时转子试件温度仍维持在1 000 K，与静子试件温差为900 K。由此可见，相对于转子试件，静子试件更易于发生着火。

图5 200 N摩擦接触压力下TF550钛合金试件不同部位的最高温度变化曲线Fig.5 Temperature variation curves of different parts of TF550 titanium alloy specimens under 200 N friction contact pressure

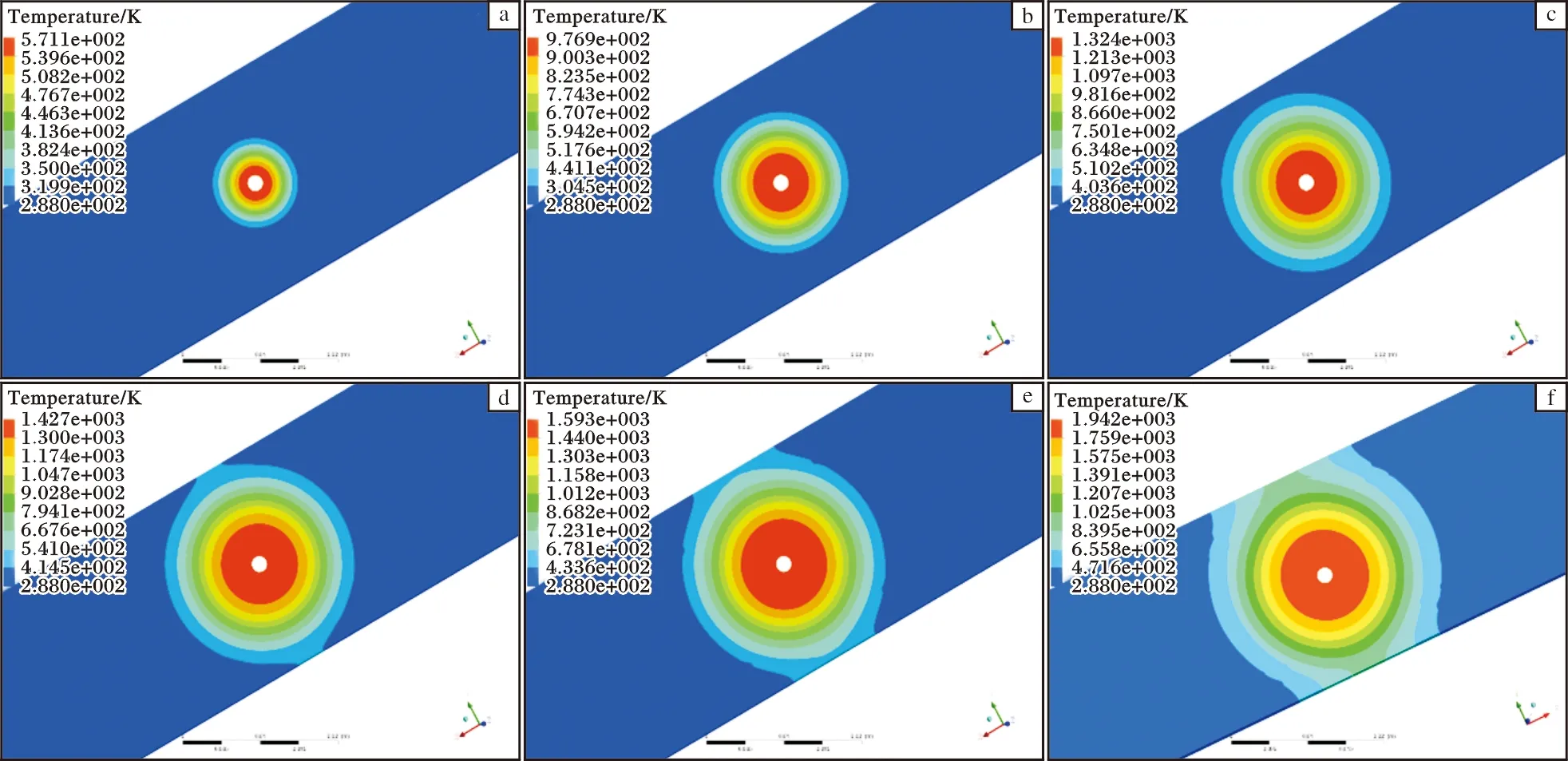
图6 200 N摩擦接触压力下TF550钛合金静子试件背面不同时间的温度场Fig.6 Temperature fields of the back of TF550 titanium alloy stator under 200 N friction contact pressure at different time:(a)0.8 s； (b)2.4 s； (c)4.0 s； (d)4.8 s； (e)5.6 s； (f)7.2 s

图7 200 N摩擦接触压力下TF550钛合金转子与静子试件接触面不同时间的温度场Fig.7 Temperature fields of the contact surfaces of TF550 titanium alloy rotor and stator under 200 N friction contact pressure at different time:(a)0.8 s； (b)2.4 s； (c)4.0 s； (d)4.8 s； (e)5.6 s； (f)7.2 s

在实际试验过程中，通过调节摩擦接触压力可以改变摩擦热源的大小，进而改变着火延迟时间。图8为有限元模拟的不同摩擦接触压力下静子试件的温度变化曲线。由图8可知，当摩擦接触压力为700 N时，在第一级转子磨损结束时(0.456 s)静子试件的最高温度接近1 400 K，而在第三级转子试件磨损开始时(2 s)静子试件温度超过2 000 K，因此在2 s内静子试件达到着火温度；当摩擦接触压力为400 N时，静子试件在3.3 s达到着火温度，相对于摩擦接触压力为200 N工况下，着火延迟时间缩短了一半。由此可见，摩擦接触压力对于着火延迟时间有一定影响，在试验过程中应尽量采取减震手段减小应力波动从而提高试验精度。

图8 有限元模拟的不同摩擦接触压力下静子试件的温度变化曲线Fig.8 Temperature variation curves of the stator achieved by finite element method under different friction contact pressure

在实际的发动机条件下，环境温度在700 K以上，因此对不同环境温度下静子试件的温度变化进行了模拟计算。图9为有限元模拟的不同环境温度下TF550钛合金静子试件的温度变化曲线。由图9可见，在823 K的环境温度下，TF550钛合金静子试件在5 s内就达到着火温度。

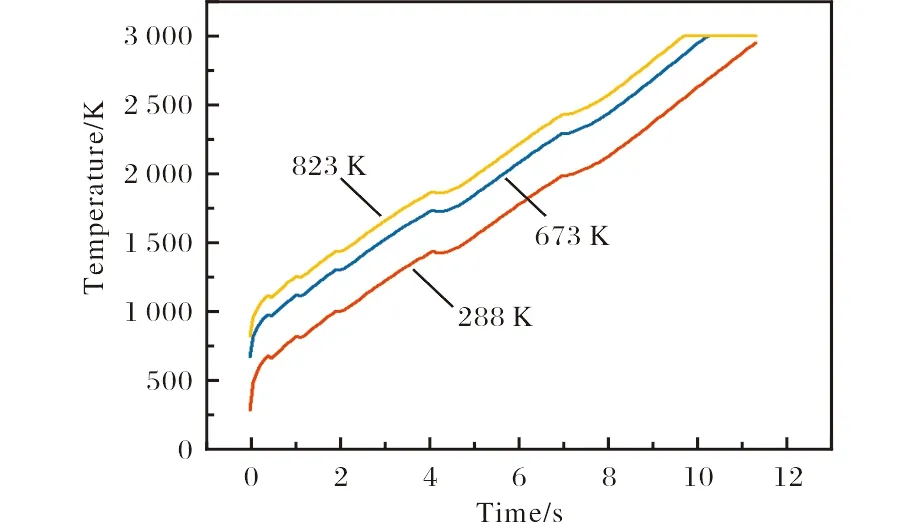
图9 有限元模拟的不同环境温度下静子试件的温度变化曲线Fig.9 Temperature variation curves of the stator achieved by finite element method under different environment temperatures

4 结 论

(1)建立了阻燃钛合金TF550摩擦着火过程的三维热-力-磨损耦合有限元模型。与TF550钛合金转子试件升温速率相比，静子试件的升温速率更快，更容易发生着火。在室温、200 N摩擦接触压力条件下，TF550钛合金静子试件在7.2 s达到着火温度，此时转子试件温度仍维持在1 000 K，比静子试件低约900 K。

(2)当摩擦接触压力从200 N增大至400 N时，TF550钛合金着火延迟时间为3.3 s，缩短了50%；在823 K环境温度下，静子试件的摩擦着火延迟时间为5 s，相比室温着火延迟时间缩短了2.2 s。相对于环境温度的影响，摩擦接触压力对TF550钛合金着火升温速率的影响更大。