橡胶管在氦质谱检漏中渗氦研究

孙开磊 许东升 甄占昌 张 聪

（火箭军工程大学，陕西 西安 710025）

氦气是惰性气体，具有化学稳定性，它在空气中的含量也非常低，约占空气的0.0005%，正因为氦气存在这种天然优良特性，所以真空检漏选用氦气作为探索性气体；氦质谱检漏是当今真空检漏的重要方法，被广泛应用到现代工业的各个领域，其原理是利用氦气作为示踪气体进行检漏，用氦气探测各类检测件的密封性能，这种检漏方法的优点不但是能够快速找到漏点，而且能定量检测漏率，精度高达10-10Pa·m3/s，但是氦气也有其自身的缺点，就是氦气是单原子气体，氦分子半径相对较小，分子运动时，很容易穿透大部分物质，例如用橡胶管作为管路检漏，管壁的组成为有机物，分子间隙大，氦分子半径较小，很容易渗透橡胶中穿过管壁，迅速扩散到质谱室，对检漏仪检测的漏率直接造成影响。

1 氦质谱检漏原理

氦质谱检漏是利用氦气作为示踪气体[1]，探测密封容器的漏率，是一种快速定位和定量检测的理想方法，对密闭容器一般采用喷氦法检漏，主要完成2 个步骤。1）用检漏仪对被检容器抽高真空，然后在容器外围喷氦气或罩氦气，容器如果有裂隙或缺陷，氦气会通过裂隙或缺陷渗漏到容器内部，并迅速扩散到检漏仪质谱室。2）利用氦质谱检漏仪进行检漏，检漏仪主要由离子源、磁极、分析器、收集极、放大器、真空设备及电气等组成，在预抽泵及分子泵工作时，仪器检内部测空间达到高真空状态，核心部件质谱室内杂质气体很少，渗漏的氦气迅速扩散到电离室，离子源电子经过加速进入电离室，在电离室内与残余气体分子和经被检件漏孔进入电离室的氦气相互碰撞使其电离成正离子，这些离子在加速电场作用下进入磁场，由于洛伦兹力作用产生偏转，形成圆弧形轨道，如图1 所示，轨道半径

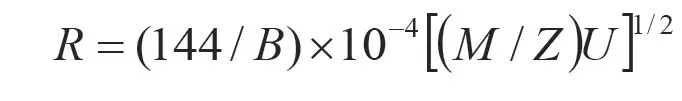
式中：R―离子偏转轨道半径，cm。

B―磁场强度，T。

M/Z―离子的质（量）/（电）荷比（正整数）。

U―离子加速电压，V。

上式中，当R、B为固定值时，改变加速电压可使不同质量的离子通过磁场和接收缝到达接收极而被检测，得到不同分子的质谱图，形成不同气体分子的峰，峰高度代表离子流强度，与相应的气体成分在电离室中的分压强成正比；氦质谱检漏仪工作时，离子加速电压设定对准氦峰，接收极只收集氦离子，所形成的氦离子流经放大后用于指示漏率的大小，比氦离子重的其他离子被全离子检测极接收。

图1 氦质谱检漏仪的质谱原理

氦质谱检漏仪对通过漏孔进入的氦气最终经过电离、加速、聚焦，全部收集到接收极，在接收极上表现为微弱的电压信号，经过放大器对信号进行多次放大、处理转换，就可以显示出漏率。

2 橡胶管渗氦实验

实验的目的如下。1）用同一橡胶管，验证不同温度与橡胶管漏率的关系。2）在等温条件下，验证橡胶管长度与漏率的关系，围绕这2 个目的，设计了以下实验。实验分2 部分进行。1）用同一橡胶管，分别在20℃、25℃温度下计时15 min，记录漏率数据。2）在20 ℃下，通过增加橡胶管长度，计时15 min，记录漏率数据。氦质谱检漏仪选用ZQJ-230D 型，校准仪器的标准漏孔为1.53×10-8Pa·m3/s，用纯度99.99%氦气作为检漏示踪气体，采用钟罩法对橡胶管进行检漏，利用氦气袋罩住橡胶管路，充高纯氦气进行实验，选取规格内径为6 mm、外径为11 mm 的真空橡胶管。

2.1 在两种温度下，验证同一橡胶管时间与漏率的关系

在T=20 ℃环境下，进行实验，记录数据并生成时间-漏率曲线，拟合漏率曲线如图2 所示。

图2 时间-漏率曲线

实验每隔30 s 记录橡胶管漏率数据，共记录30 组；由以上时间—漏率曲线可以看出，检漏仪开始检漏3 min 后检测到渗漏的氦气，随着时间推移，氦气渗漏量不断增加，漏率显著提高，时间—漏率是正相关曲线。

在T=25 ℃环境下进行实验，记录数据并生成时间-漏率曲线，拟合漏率曲线如图3 所示。

图3 时间-漏率曲线

该组数据是在温度为25 ℃下进行测量的，漏率数值总体比20℃时偏高，原因是由于温度升高后，氦分子热运动加强、分子运动速度快，导致渗透量增加，反映在检漏仪上就是漏率偏大。

2.2 漏率与橡胶管长度的关系

在T=20℃的条件下，通过增加橡胶管长度，验证漏率与橡胶管长度的关系。

选择长度为100 mm、内径为6 mm、外径为11.5 mm 的橡胶管，在室温20 ℃环境下进行实验，拟合时间—漏率曲线如图4 所示。

从该组数据可以看出，增加橡胶管长度，橡胶管的漏率显著增加，仅6 min，漏率达到1.2×10-7Pa·m3/s，是前者的100 多倍，由于仪器的保护，很难再进行测量。

图4 时间-漏率曲线

3 理论分析

橡胶主要是由橡胶烃组成的，是高分子化合物，一般分子量达到几十万，氦气是单质小分子，所以它很容易从大分子间隙中通过；氦气渗透橡胶是一种物理现象，实际上氦气在橡胶管中经历了溶解、扩散与渗透的过程，一般用亨利定律来研究气体扩散规律，公式为：

C=SP

式中：C—气体在固体中的溶解度。S—一个大气压下的溶解度。P—环境气体压力。

由以上公式可知，橡胶能溶解氦气，在等温条件下，气体在橡胶中的溶解度与氦气压力成正比。

氦气进入橡胶扩散还遵循菲克第一定律和第二定律，第一定律可知单位时间通过单位面积扩散的气体量为

D—扩散系数，cm3/s；

菲克第二定律：在氦气扩散过程中，橡胶材料内溶解气体的浓度不但是位置x的函数，而随着时间t而变化，即C=C（x，t）。若扩散系数D与x无关，则浓度随时间t的变化率为

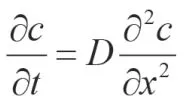
扩散系数D由氦气橡胶组合的性质决定，是标志扩散的基本参量。此外，它又是温度的指数函数，即

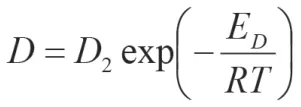
式中：D2给定气体的材料常数；ED—扩散激活能；exp—常数指数e，R—理想气体常数，T—温度。

由此可见：温度越高氦气扩散的越快；初始氦气浓度越高扩散的气体量也越大。

4 结论

通过实验，直观的反映时间-漏率是正相关函数，同等长度橡胶管温度越高，氦分子扩散速度越快，漏率越大；在同等环境条件下，改变橡胶管长度，长橡胶管的漏率更大；通过菲克定律理论分析，进一步支撑了实验数据。

因此，对氦质谱检漏实验者提出建议，使用钟罩法检漏时，尽量避免使用橡胶管作为检漏管路，如果不可避免使用时，应尽量使橡胶管不参与氦气部分的检漏；通过实验还可以观察到氦气穿透壁厚5 mm 橡胶管的运动时间约3 min，建议喷氦法检漏时，橡胶部位喷氦时间要短，检漏人员要注意把控好时间差，尽可能在3 min 内喷氦检漏完毕，这样就增加了检漏结果的可信度。