基于Monte-Carlo拟合的二维随机载荷作用下汽车弹簧疲劳耐久性研究

藤瑞品，宋晓琳，刘国云，曾俊伟

（1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.湖南猎豹汽车股份有限公司，长沙 410100）

前言

汽车在工作时受到的载荷谱是一个随机过程，随机载荷的表征参数包含载荷幅值和载荷均值，疲劳耐久的研究应基于载荷幅值和均值都为随机变量的二维随机载荷进行。

陈欣等［1］对汽车传动系统的载荷谱进行了研究，基于幅值和频次的关系建立了八级程序载荷谱；高云凯等［2］通过将二维程序载荷谱简化为一维程序载荷谱，建立了车身疲劳试验程序载荷谱；高孝旺［3］在基于载荷幅值为威布尔分布的基础上分析了三参数威布尔分布的3个参数对等效载荷和相关评价参数的影响趋势；胡建军等［4］以随机载荷为输入对齿轮的疲劳寿命进行了试验研究；武滢和谢里阳［5］基于载荷幅值和均值都为随机分布的情况下以其联合概率密度为基础建立了疲劳寿命的分布预测模型。金星等［6］对随机疲劳裂纹进行了研究，提出了一种疲劳裂纹扩展的新模型。邹小理［7］提出了一个随机荷载作用下疲劳裂纹扩展的统计模型。郭虎等［8］通过对汽车前桥载荷进行采集，得出了在各种路面下等效载荷的分布符合三参数威布尔分布的结论。贺小帆等［9］以独立多细节结构概率失效模型为基础，进行MonteCarlo抽样，对独立多细节结构的寿命分布特性进行了检验；朱颖等［10］提出一种计算平稳高斯荷载作用下不确定结构疲劳损伤的新方法。

目前对于汽车的疲劳耐久的研究绝大部分是基于循环加载的方式，对于一维随机载荷作用下的疲劳耐久也有过一些研究，对于二维随机载荷作用下的疲劳耐久的研究不够深入，没有成熟的方法和理论。对于考虑载荷幅值和载荷均值各自的随机特性的疲劳耐久的研究尚未见相关文献报道。

在进行疲劳分析时，一些相关数据由于各种实际条件限制难以准确得到，而参数拟合是一种可行的近似方法。如黄学伟等［11］提出了一种预测材料与结构裂纹在高周疲劳下疲劳裂纹扩展速率的数值模拟新方法；田秀云等［12］提出了一种金属材料疲劳裂纹扩展曲线的拟合方法等。

1 二维随机载荷作用下的疲劳损伤

根据Goodman公式，当量载荷Seq的表达式［13］为

式中：σb为材料的拉伸强度；Sa为载荷幅值；Sm为载荷均值。

设随机变量X和Y相互独立，其概率密度函数分别为fX（x）和fY（y），则的概率密度函数fZ（z）［14］为

根据Miner定则［15-17］，累积疲劳损伤的计算方法为

式中：D为材料的累积疲劳损伤；N为材料受到的循环载荷总数量；S为材料受到的当量载荷；f（S）为随机当量载荷的概率密度函数；Nf为材料在载荷S作用下的疲劳寿命。

2 二维随机载荷的当量载荷的概率密度函数

2.1 概率密度函数的代数法推导

利用载荷幅值和载荷均值的概率密度以及当量载荷和载荷幅值、载荷均值之间的数学关系可对当量载荷的概率密度函数进行推导，如文献［18］中推导得到了载荷幅值和载荷均值均符合正态分布的二维随机载荷的当量载荷的概率密度函数。

2.2 概率密度函数的Monte-Carlo拟合

2.2.1 Monte-Carlo拟合方法和分布参数选择

采用数学方法推导二维随机载荷的当量载荷的概率密度函数在实际应用中存在很多局限性：一方面推导过程一般都比较繁琐；另外在采用Goodman公式求当量载荷的概率密度函数时，很多情况下无法用数学方法直接推导得出。

蒙特卡洛法［19-23］也称为随机模拟法，是通过生成随机数序列（实际上应该为伪随机数）来对数学问题进行拟合分析的一种数值方法。假设随机载荷谱的载荷均值和载荷幅值的分布律和概率密度函数都已知，则可通过采用蒙特卡罗法随机生成载荷幅值和载荷均值数据并得到当量载荷的随机序列，并分析得到当量载荷的随机分布特性。

在试验场对某城市SUV进行载荷谱采集，得到40个通道的应变时间历程信号，采用雨流计数法［24-28］对载荷谱时间历程曲线进行计数处理，得到包含不同载荷幅值和载荷均值以及各自所对应的计数频次的载荷谱。进行参数估计和分布检验可得，载荷幅值基本上符合两参数威布尔分布，载荷均值基本符合正态分布。

设载荷幅值Sa符合二参数威布尔分布，其形状参数为α，尺度参数为β；载荷均值Sm符合正态分布，分布参数标准差为σ，均值为μ，根据随机变量的函数的分布特性，载荷均值Sm的函数同样符合正态分布，分布参数中，标准差为，均值为

选取用于当量载荷概率密度函数数值拟合研究的载荷幅值和载荷均值的分布参数范围，如表1所示。

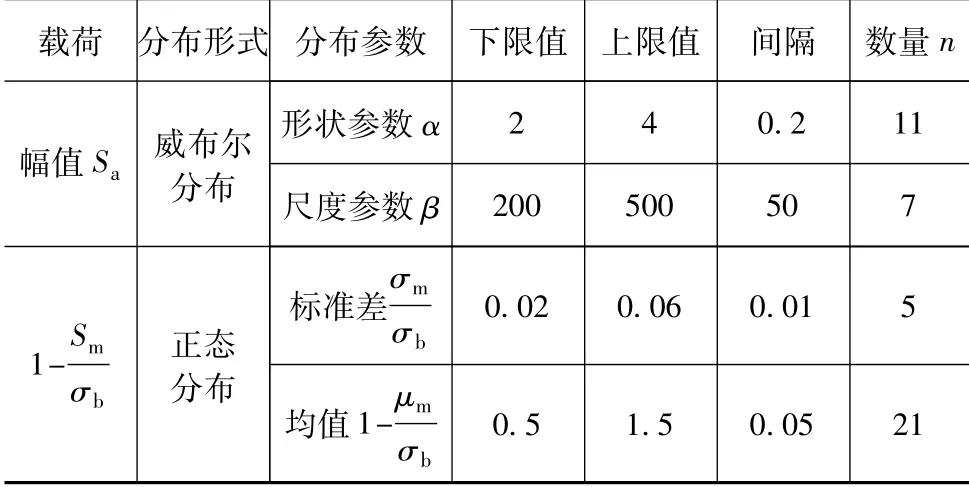
表1 分布参数范围

为研究不同分布参数的影响，共选取表中8 085组分布参数进行了数值拟合的研究。

2.2.2 随机载荷序列的生成

采用蒙特卡罗法对表1中分布参数进行随机生成，得到载荷幅值和载荷均值的随机序列ui和vi，再采用Goodman公式进行一维随机载荷的零均值当量载荷的转化，得到随机当量载荷序列为fi，则fi的生成方法为

式中vi为符合正态分布的载荷均值的函数所生成的随机序列。

2.2.3 参数估计

（1）图形估计［29］

对表1中的不同分布参数的随机当量载荷序列fi进行WPP（威布尔概率图）分布检验，检验结果发现采用威布尔分布形式来对随机载荷序列fi进行拟合的效果较好，图1表示一组参数仿真后的图形法估计参数的结果。

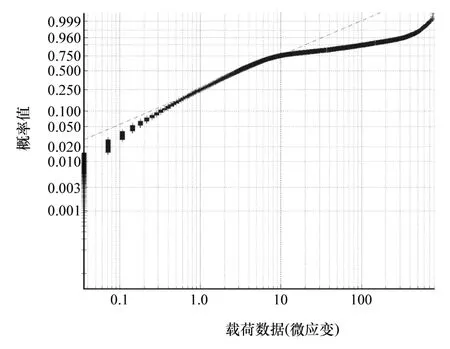
图1 图形法估计参数

（2）分布参数估计

采用最大似然法对符合表1中的二维随机载荷的零均值当量载荷的拟合分布进行未知分布参数估计，拟合得到符合威布尔分布的当量载荷的分布参数，包含形状参数α和尺度参数β。

表2为部分拟合的分布参数数据。

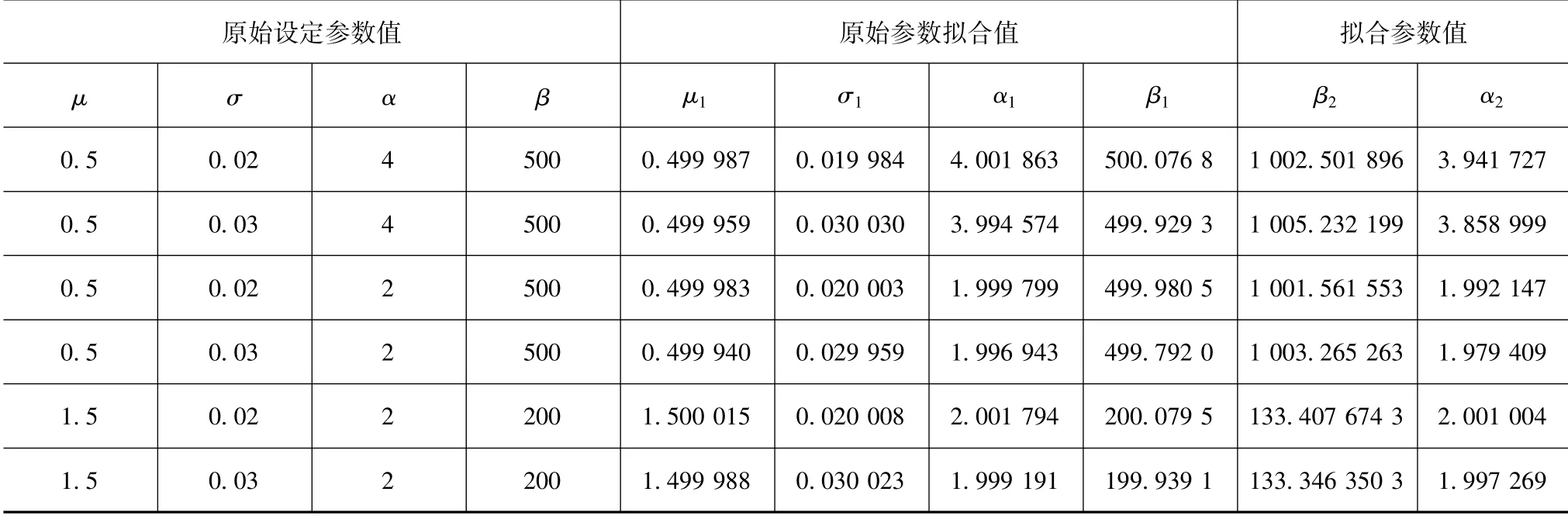
表2 分布参数拟合

由表2中的数据可以看出，采用通过蒙特卡罗法生成的随机序列对载荷幅值和载荷均值的分布函数的分布参数进行拟合，拟合得到的分布参数值与原始定义的分布参数值基本相符，由此验证了蒙特卡罗拟合法的正确性。

3 载荷谱数据采集和处理

3.1 载荷谱数据的采集

采用4个车轮六分力传感器、10个加速度传感器和38个应变片传感器，在襄阳试验场的石块路面采集了某城市SUV车型整车主要结构载荷谱。

3.2 载荷谱数据的处理［30-34］

原始载荷谱为包含异常点（毛刺）以及连接路面的信号的时间历程曲线，须将异常数据和连接路面的数据剔除，左前螺旋弹簧经处理后的数据信号如图2所示。

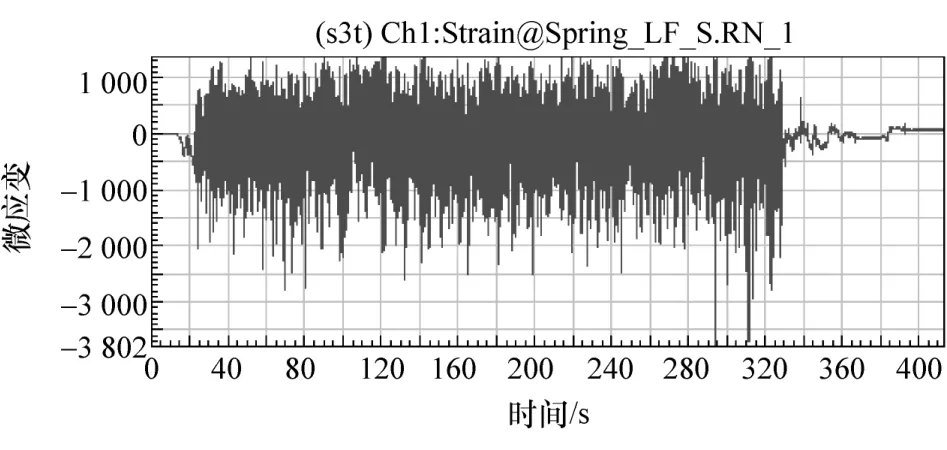
图2 左前弹簧载荷谱信号

对载荷谱时间历程采用雨流计数法统计处理，形成包含幅值和均值以及各自的统计计数信息的三维直方图，左前螺旋弹簧的载荷谱三维直方图如图3所示。

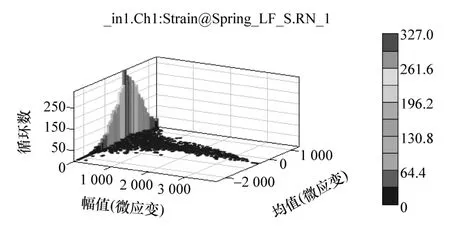
图3 左前弹簧载荷三维统计直方图

左前螺旋弹簧的载荷幅值和均值各自的二维统计直方图如图4和图5所示。

3.3 统计模型的图形法检验［29-35］

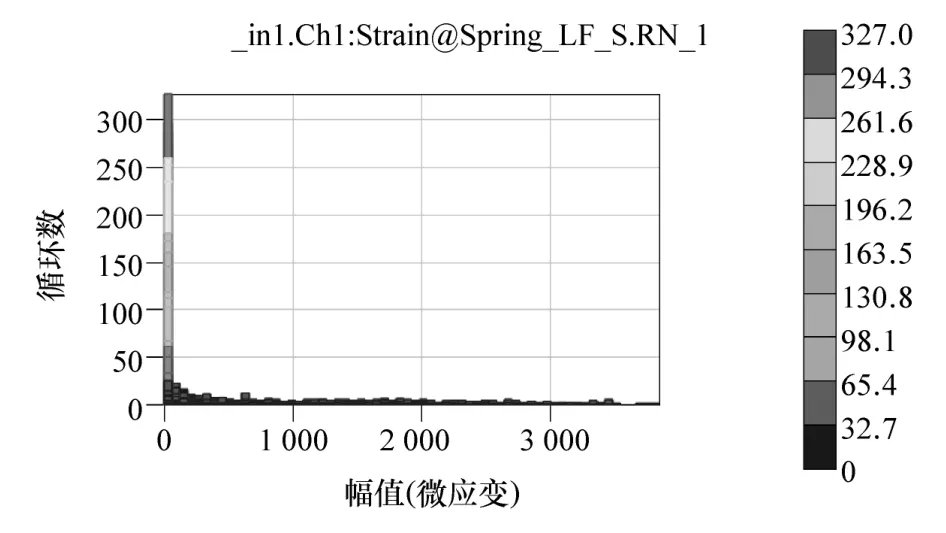
图4 左前弹簧载荷幅值统计直方图

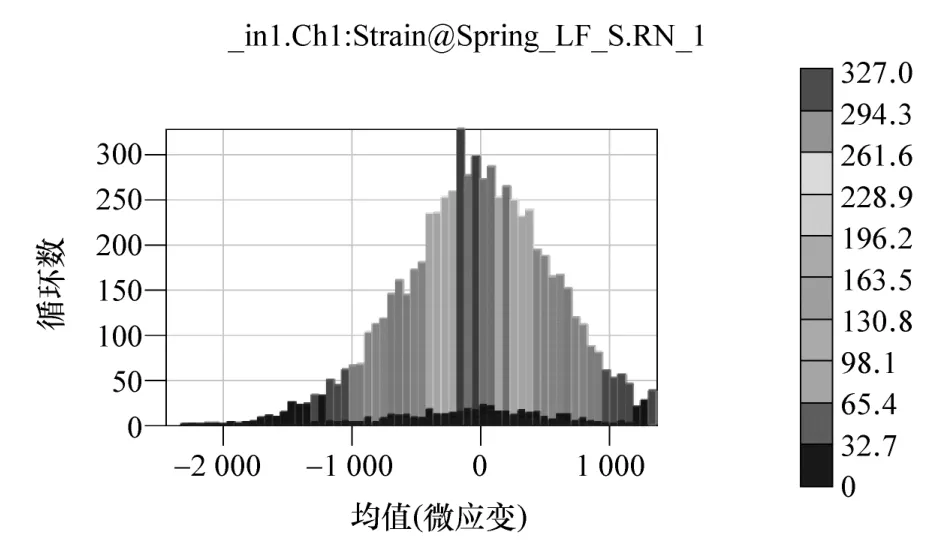
图5 左前弹簧载荷均值统计直方图

为了确定载荷谱数据是否服从威布尔分布和正态分布，可以用相应的概率图去检验。

经过雨流计数法统计右前螺旋弹簧的载荷谱的幅值和均值，进行威布尔和正态分布的图形检验的结果见图6和图7。

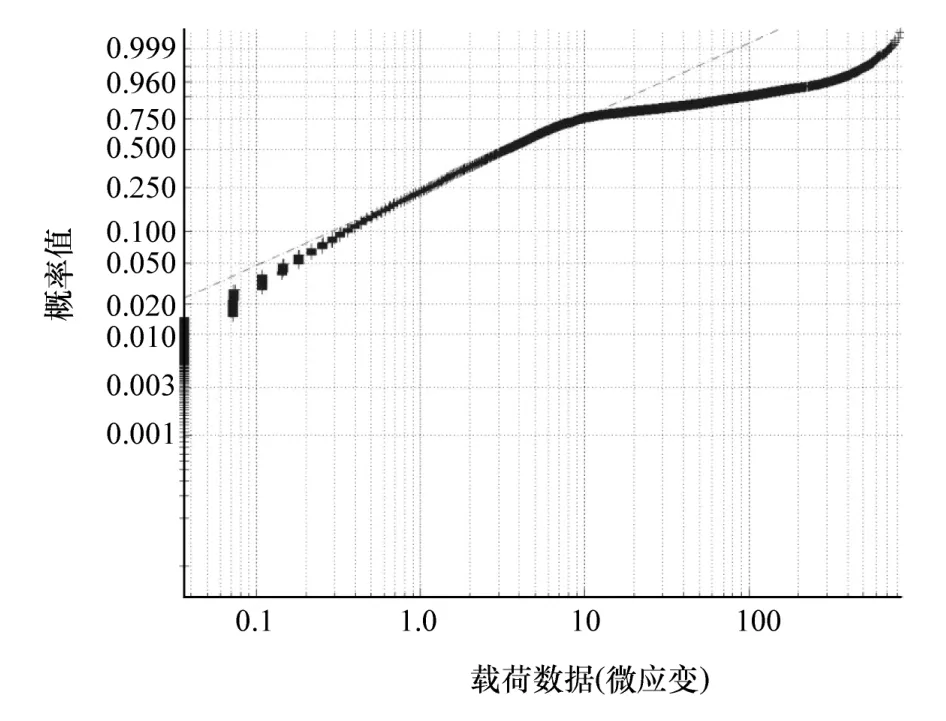
图6 威布尔分布检验图

通过观察发现，图6中除了部分比较小的幅值和总体趋势不一致外，其它基本符合威布尔分布的假设。而通过观察图7可知，均值非常符合正态分布的假设，这与图5的直方图一致。

采用极大似然对模型的分布参数进行估计［14］，部分参数估计的结果见表3。

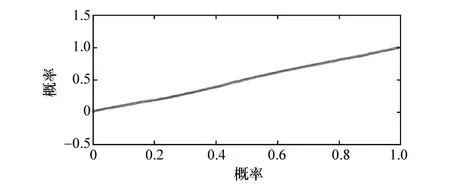
图7 正态分布检验图

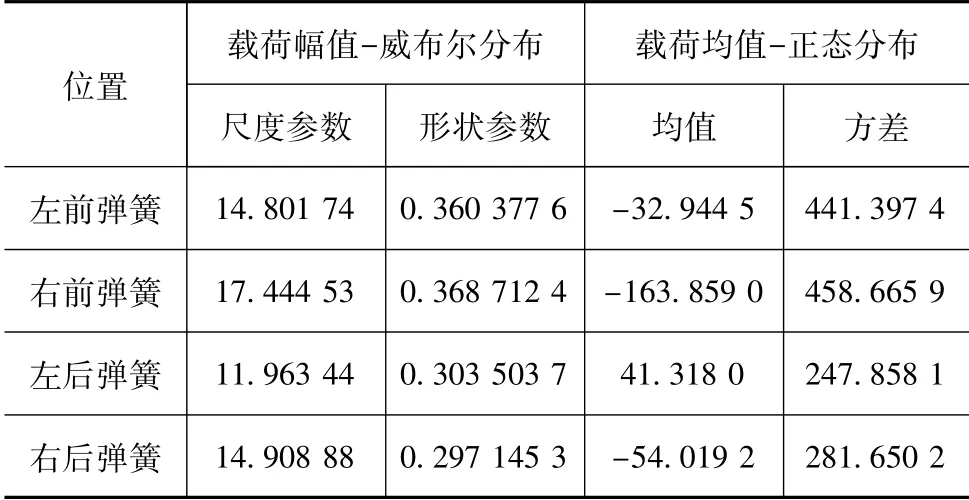
表3 统计分布参数

其它测试点的载荷分布特性与表中类似，即载荷幅值符合威布尔分布，载荷均值符合正态分布。

4 疲劳损伤与耐久寿命分析

4.1 载荷谱数据样本的截除

根据参数估计对载荷谱进行图形法检验时，发现低载荷区域和高载荷区域都发生了较大的偏离，由于高载荷区域对整个疲劳寿命的预测影响较大，因此采用这种方法外推的载荷谱用于疲劳损伤计算会产生较大的误差。

由于在载荷谱采集时采集了大量的小载荷，绝大部分小载荷低于疲劳极限，因此并不会对疲劳损伤带来影响，而大量的小载荷会对随机分布的参数估计造成较大影响，因此采用将小载荷去除的方法将样本进行截断，采用截断后的样本进行随机分布的参数估计。

图8～图10分别为右前螺旋弹簧载荷数据在未截除状态、截除100 MPa以下和截除400 MPa以下数据后的估计参数检验图形。

由图可知，右前螺旋弹簧的载荷数据在截除100 MPa以下的小载荷后，估计参数在中高载荷部分可实现很高的拟合度。

按同样的方法对表3中数据进行截取后的拟合参数见表4。

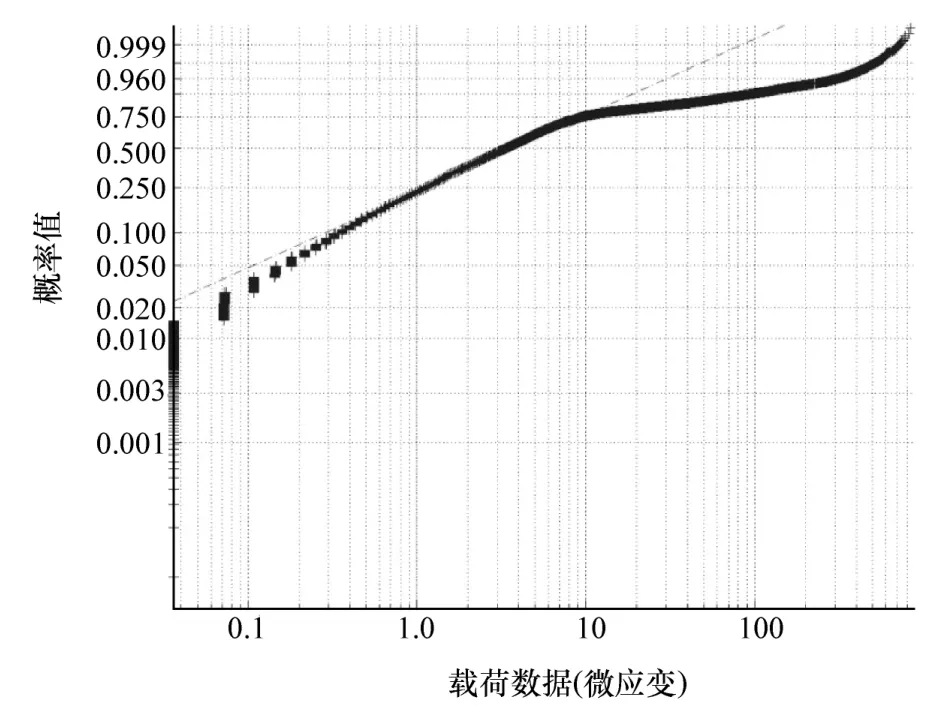
图8 原始数据参数估计

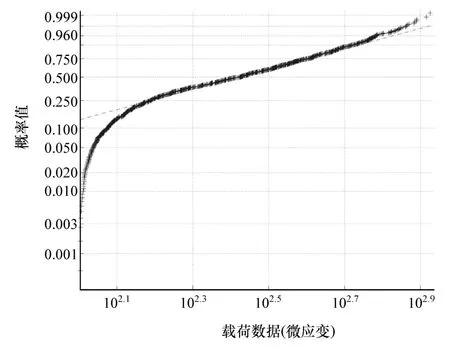
图9 截除100 MPa以下小载荷

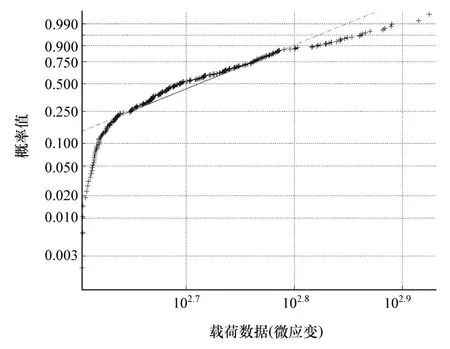
图10 截除400 MPa以下载荷

对样本截除后拟合参数进行参数检验，在中高载荷部分均可实现很高的拟合度。

4.2 随机载荷谱的外推

以石块路工况的4个螺旋弹簧零件的载荷谱数据为研究对象，对随机载荷谱进行外推。石块路总长度为2.7 km，耐久试验总目标里程目标值为10 000 km。4个弹簧载荷在样本截取后的单次试验循环里程的载荷样本数和10 000 km的累计载荷循环数见表5。

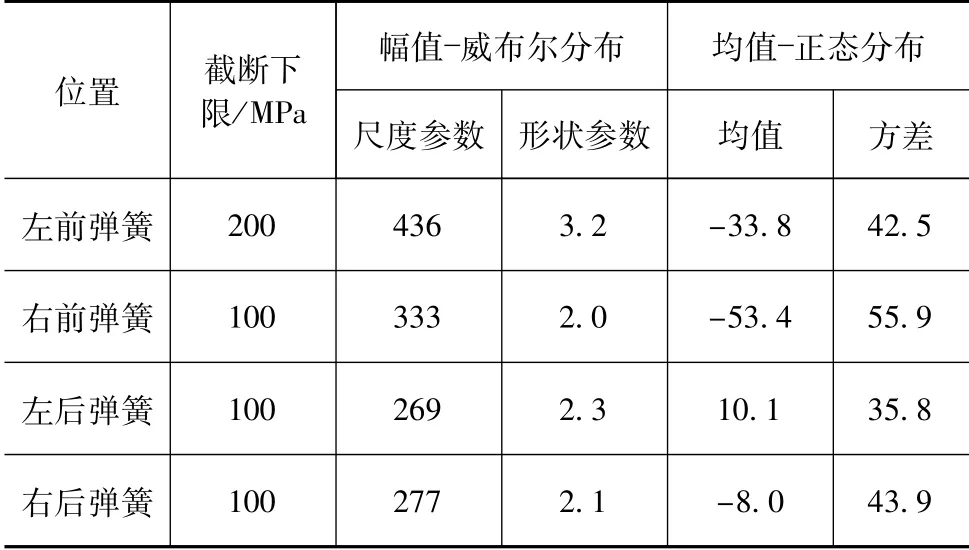
表4 样本截除后的分布参数

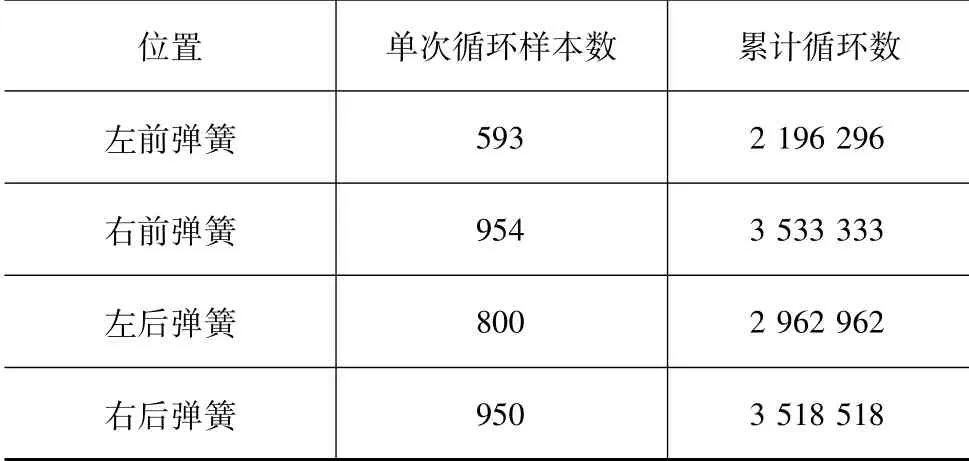
表5 载荷循环计数

根据分布参数的估计结果，载荷幅值基本上都符合威布尔分布，但形状参数都不等于1，用传统的数学方法无法推导出当量载荷的概率密度函数，所以采用Monte-Carlo法进行拟合。

4.3 累计损伤计算

4.3.1 材料的S-N曲线拟合

在没有真实的S-N曲线可用时，根据已有的试验数据和素材，对材料的S-N曲线进行估算和拟合，可以作为工程实践中进行疲劳耐久设计的一种近似手段。

S-N曲线的拟合方法主要有两种：三参数公式［13，36-38］和分段拟合法［39，43］。

弹簧钢材料为60Si2Mn，抗拉强度为1 625 MPa［44］，疲劳极限为660 MPa，采用分段拟合法拟合S-N曲线见图11。

图11中，S1000和Sbe分别为材料在标准循环加载103和106次的疲劳强度，Sf为材料的抗拉强度。

对于钢材料，S1000取0.72Sf。拟合得到高周疲劳区疲劳寿命Nfh与名义应力幅Sa的关系式为

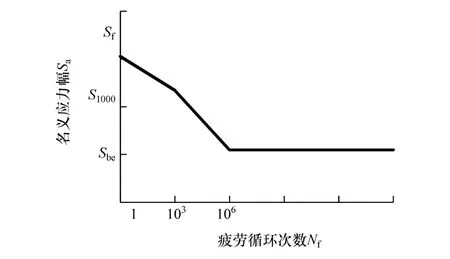
图11 S-N曲线分段拟合

低周疲劳区疲劳寿命Nfl与名义应力幅Sa的关系式为

4.3.2 蒙特卡罗拟合法累积损伤计算

蒙特卡罗法拟合螺旋弹簧的分布数据见表6。

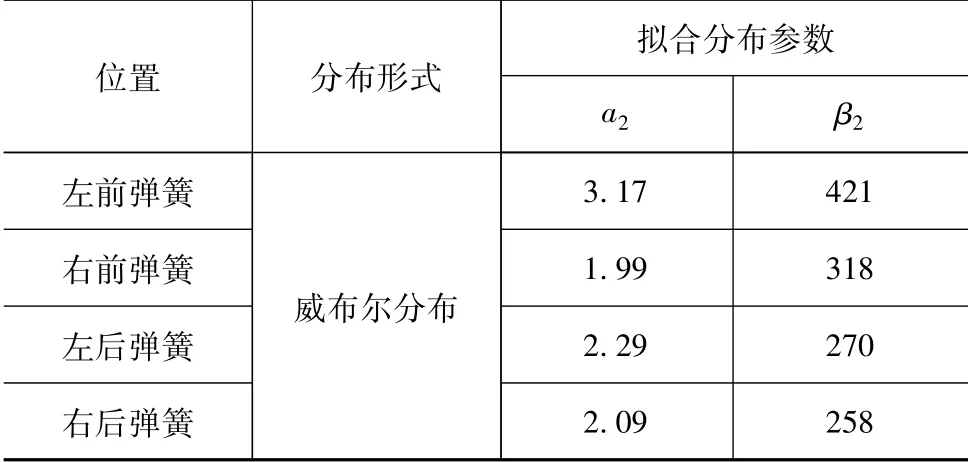
表6 拟合分布参数

可得左前、右前、左后和右后4个螺旋弹簧的当量载荷的概率密度函数f1（S1），f2（S2），f3（S3）和f4（S4）：

根据式（3）可得

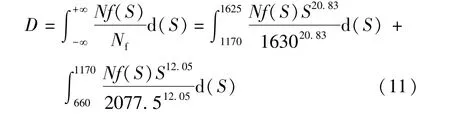
当累积疲劳损伤D＝1时，可得疲劳寿命N为

由式（7）～式（10）4个螺旋弹簧的零均值一维当量随机载荷谱的概率密度函数可得4个螺旋弹簧的疲劳寿命N1～N4，分别为

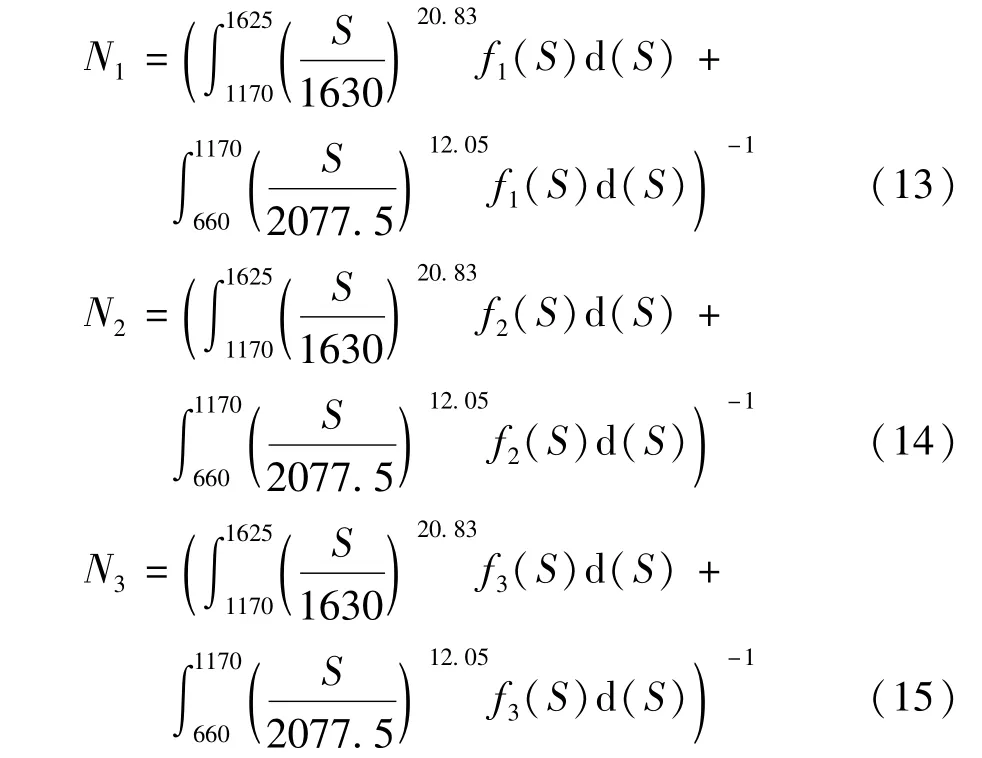
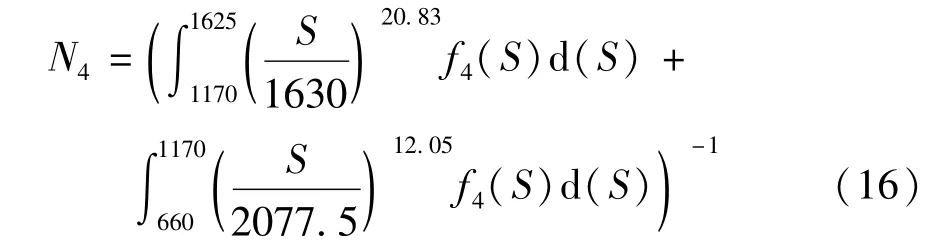
采用八点高斯-勒让德求积公式［45］进行积分运算，得到4个螺旋弹簧的疲劳寿命。以N1的计算为例，计算方法如下。

将累计损伤D分为D1和D2两个阶段，则

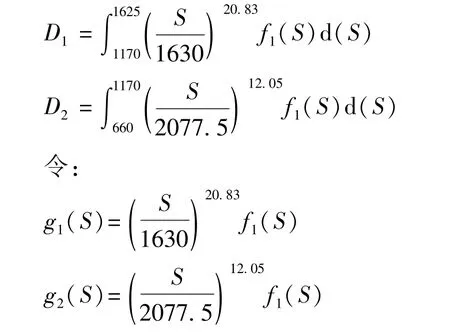
首先计算D1，根据D1的积分范围［1 170，1 625］计算得到8个积分计算点，见表7。其中Si为积分计算点，i＝1，2，…，8。计算过程和结果见表8。

表7 积分点

表8 求积计算结果

因此可求得

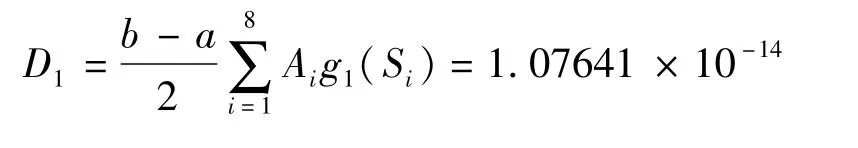
同样的方法求得

D2＝4.43738×10-8

由此可算得左前螺旋弹簧的疲劳寿命N1：

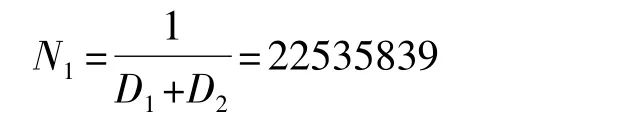
同样的方法求得右前、左后和右后螺旋弹簧的疲劳寿命N2，N3和N4分别为：N2＝9429618，N3＝1020328144，N4＝446309357。

根据表5中的每10 000 km的载荷循环数，可以得到4个螺旋弹簧的总耐久寿命里程，见表9。

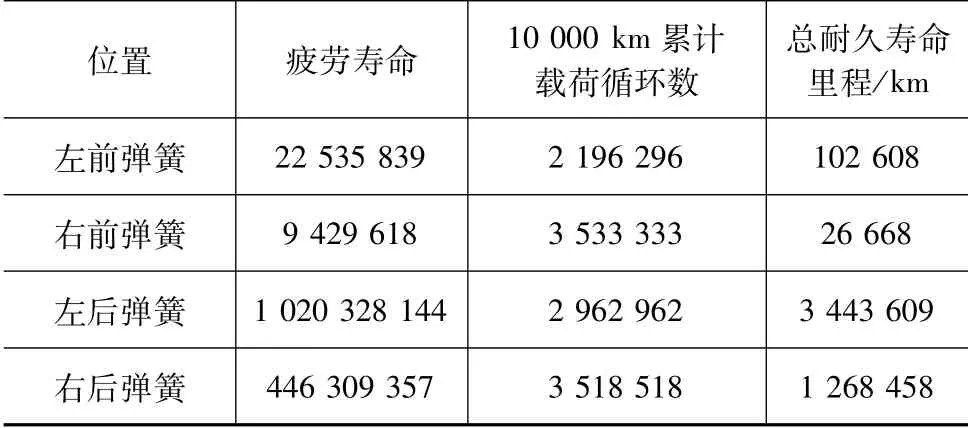
表9 耐久寿命里程

4.3.3 载荷谱分级法累积损伤计算［2］

为了进行比较，同时采用载荷谱分级法对疲劳寿命进行计算。

载荷的分级会影响损伤计算结果，研究不同的载荷分级状态下的疲劳损伤结果表明，当载荷分级大于40级时，计算结果趋于稳定。

采用50×50级载荷分级，计算4个弹簧的损伤和疲劳寿命，数据见表10。

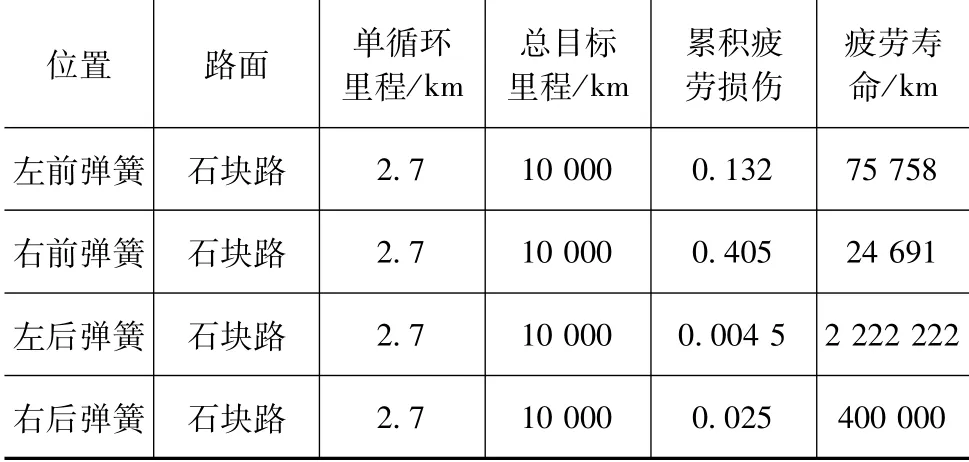
表10 累积损伤和疲劳寿命计算

4.4 疲劳寿命结果的分析比较

采用两种方法计算的疲劳寿命比较见表11。

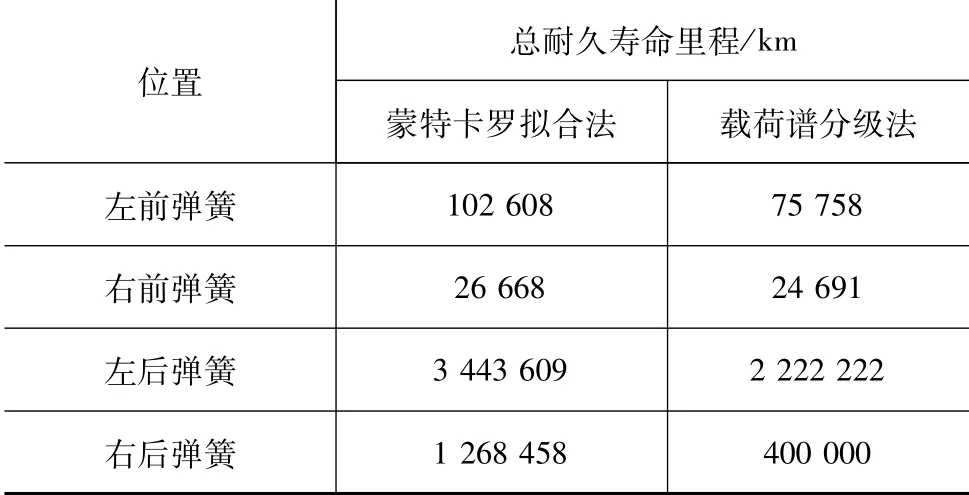
表11 总耐久寿命里程

根据表11的结果，采用载荷谱分级法计算得到的疲劳寿命相对于采用蒙特卡罗拟合概率密度函数外推法的计算结果要保守，但采用两种方法的计算结果没有数量级的差别，对于疲劳耐久分析来说误差在可接受范围之内，验证了总体耐久寿命分析结果的可信度。由于采用载荷谱分级法的计算结果与载荷谱的分级状态有关，而采用概率密度函数法计算结果唯一，通过修正分布参数可以得到较为准确的结果，且易实现程序化计算，因此概率密度函数外推法比采用载荷谱分级法具有较明显的优势。

4.5 误差原因分析

导致疲劳寿命计算结果产生误差的主要原因有如下几点：

（1）拟合的S-N曲线与实际的S-N曲线之间存在误差；

（2）估计参数与实际分布参数之间存在误差；

（3）实际载荷谱采集时，取样数据为大量不连续的载荷，计算时将其近似为连续的载荷谱进行积分运算，导致计算结果产生误差。

5 结论

（1）提出了采用蒙特卡罗法生成随机序列对二维随机载荷的当量载荷的概率密度函数进行拟合的方法，对不同分布参数的8 085组数据进行了概率密度函数的拟合研究，研究表明采用该方法拟合当量载荷的概率密度函数是可行的。

（2）采集了一款城市SUV在试验场强化路面的载荷谱数据，提出了采用样本截断方法进行随机载荷谱参数估计的方法。参数检验结果表明，在中高载荷段，样本截断法可以很好地实现对所采载荷谱数据的拟合。

（3）提出了采用二维随机载荷的等效载荷的概率密度函数进行数值积分的疲劳寿命的计算方法。以4个螺旋弹簧为研究对象，分别采用载荷谱分级法和概率密度函数积分法两种方法对所采集的二维随机载荷进行外推并计算了累积损伤和疲劳寿命，对采用两种方法计算的结果进行了对比分析，结果表明，采用两种方法的计算结果没有数量级的差别，对于疲劳耐久分析来说误差在可接受范围之内，互相证实了总体耐久寿命分析结果的可信度，也证实了通过采用蒙特卡罗法拟合二维随机载荷的当量载荷的概率密度函数来计算疲劳寿命的方法是可行的，该方法可以很好地解决分布情况较复杂的二维随机载荷的概率密度函数无法推导的问题。