曲线模型预测法在财政专项扶贫资金预测上的运用
2020-01-03陈德怀
陈德怀

[摘 要]文章采用时间序列预测长期趋势的方法,以百色市财政专项扶贫资金实际决算数据建立数学模型进行实际预测,对“十四五”规划具有理论价值和现实意义。当前决战决胜脱贫攻坚工作进入关键阶段,在财政专项扶贫资金预算工作中需要用科学的方法作为指导,为各级政府提供决策支持,提高财政专项扶贫资金的效果和效率,使稀缺的经济资源得到优化组合和合理利用。通过财政专项扶贫资金的投资,实现左右江革命老区人民脱贫致富奔小康的和谐社会。
[关键词]曲线模型;专项扶贫资金;数字模型
1 引言
为深入贯彻落实习近平总书记在决战决胜脱贫攻坚座谈会上的重要讲话精神和党中央、国务院脱贫攻坚决策部署,推动脱贫攻坚相关项目及早落实见效,确保如期高质量打赢脱贫攻坚战,中央国家财政专项扶贫资金以上级补助的方式投入到农村扶贫的第一线。地方政府预算内安排的财政专项扶贫资金占整个扶贫攻坚配套资金总量的比重较大。文章研究百色市财政专项扶贫资金在“十四五”期间的趋势预测模型,旨在为本地地方政府在财政专项扶贫资金预算安排中提供决策依据,使稀缺的经济资源得到优化与合理利用,提高财政专项扶贫资金的使用效果和效率。
2 背景
①2020年3月6日,习近平总书记在“决战决胜脱贫攻坚座谈会”上的讲话中指出:“中央财政要继续增加专项扶贫资金规模,各级财政也要保证脱贫攻坚的资金需求。” ②国务院关于同意设立广西百色重点开发开放试验区的批复国函〔2020〕34号文,批复中指出:试验区“有利于全面打赢脱贫攻坚战,加快左右江革命老区振兴发展;有利于加快边境地区城乡建设,促进稳边安边兴边,全力推进脱贫攻坚和乡村振兴”。③中共广西壮族自治区委员会办公厅厅发〔2020〕8号文“全区各地各部门要把学习贯彻习近平总书记重要讲话精神作为当前和今后一個时期的重要政治任务,一鼓作气、乘势而上,奋力夺取脱贫攻坚战全面胜利,确保与全国同步,全面建成小康社会”。
3 百色市的区位优势
百色市位于广西壮族自治区西部,右江上游,介于东经104°28′~107°54′,北纬22°51′~25°07′。总面积3.6252万平方千米,西与云南相接,北与贵州毗邻,东与广西壮族自治区首府南宁紧连,南与越南接壤,边境线长达365千米,是滇、黔、桂三地区的中心城市,是中国大西南通往太平洋地区出海通道的“黄金走廊”。
在认真贯彻落实国家、自治区关于全面打赢脱贫攻坚战,全面建成小康社会指示精神的背景下,百色市要抓住国家的宏观大政方针、政策的大好有利发展机遇,加快步伐将百色市建设成为中国—中南半岛经济走廊。投资、消费、贸易是拉动经济增长的“三驾马车”。选择国家财政专项扶贫资金项目支出上的预测,以百色市财政专项扶贫资金投入为主要研究对象,对百色市2020年完成左右江革命老区人民脱贫致富奔小康具有理论价值和现实意义。在为今后地方政府制定科学的扶贫政策起到参考。根据中央政府关于“加大财政涉农资金整合力度,加强扶贫资金监管,提高资金使用效率和效益,用好扶贫的土地和金融政策”的规定,曲线模型预测法在财政专项扶贫资金预测上的运用,为百色市地方财政部门安排年度财政专项扶贫资金预算时提供了具有操作性的科学方法。
4 曲线模型预测法的运用
马克思说:“一定的生产决定一定的消费、分配、交换和这些不同要素相互间的一定关系。当然,生产就其片面形式来说,也决定于其他因素”。财政是一个分配范畴,会受到生产的制约,同时又反过来积极影响生产。
百色市财政专项扶贫资金是地方财政总预算中的一个重要成分,占总预算资金支出的5.16%,为了充分发挥财政的分配职能作用,合理分配地方财政专项扶贫资金,调整农业产业结构,积极发展地方经济,政府职能部门的广大干部职工要解放思想,转变观念,由原来的事后检查和监督转变为事前的预测和评价,用决策支持系统工作。
财政专项扶贫资金预测是一项基础性的工作,科学与否直接关系到扶贫预算的顺利进行。因此,每年在对国家扶贫经济政策进行定性研究的同时,还必须进行定量分析。经济数学模型在财政专项扶贫资金预测中的运用,提出了有预见性的科学依据,运用这一手段,可以为政府和财政、扶贫管理部门所进行的经济决策、计划管理和指导实践工作提供帮助。文章根据近几十年的财政专项扶贫资金的管理经验,通过建立数学模型来预测今后财政专项扶贫资金的支出趋势。
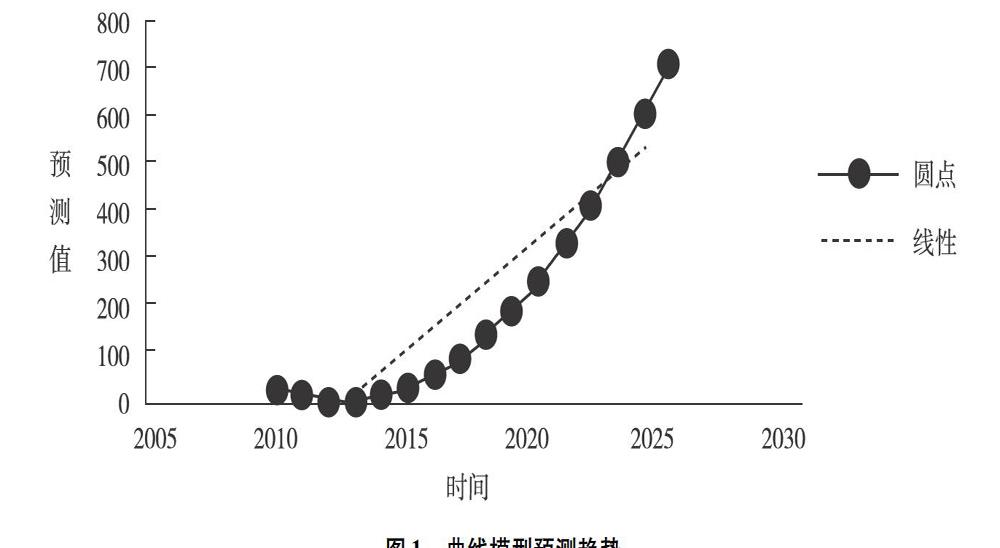
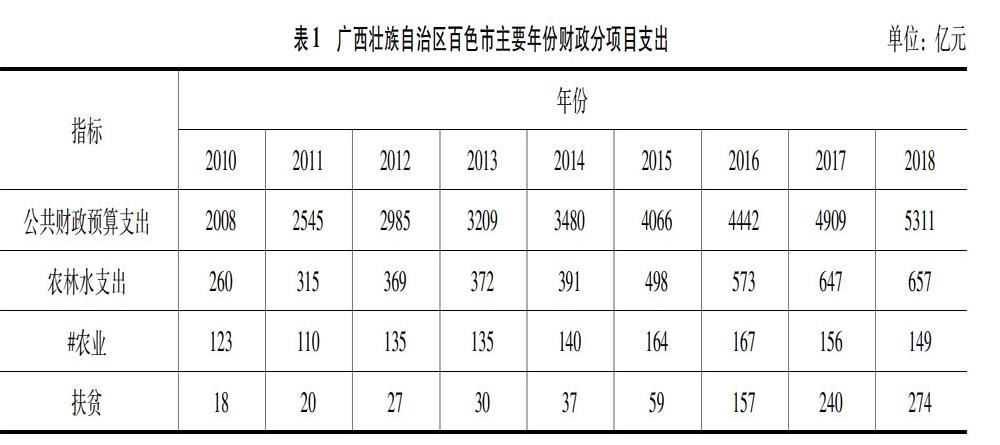
趋势曲线模型预测法是长期趋势预测的主要方法。它根据时间序列的发展趋势,配合合适的曲线模型预测未来的趋势。根据百色市2010—2018年的决算资料,用三点法预测百色市“十四五”期间财政专项扶贫资金支出增长趋势(速度),为财政专项扶贫资金预算提供参考。
4.1 收集数据分析整理
从表1可以看出,扶贫资金占公共财政预算支出的5.16%、农林水支出的41.70%。由此可见,扶贫资金的投入占整个大农业的一半,对于改变左右江革命老区的贫困面貌将起到举足轻重的作用。
4.2 选择预测模型
计算序列的一阶、二阶差分,列于表2中。从表2计算结果可看出,二阶差分是基本平稳的,因此可配合二次抛物线预测模型来预测。
4.3 建立二次抛物线预测模型
4.4 预测
先计算Sy,将表3计算结果代入,便得:
5 结论
将数学模型储存于计算机,利用统计分析研究软件,如SPSS、STATA、R等软件,即可预测“十四五”期间百色市财政专项扶贫资金需求量,发展速度和增长速度,在安排财政专项扶贫资金预算工作过程中作出最佳决策。
参考文献:
[1]马克思.资本论:第 1 卷[M].北京:人民出版社,2003.
[2]马克思.资本论:第 3 卷[M].北京:人民出版社,2004.
[3]杨彤.刍议精准扶贫的财政支持[J].河南工业大学学报(社会科学版),2019,15(3):73-77.
