阻尼比对水电站厂房结构脉动压力数值计算的影响

陈 鹏，方 丹，李良权

(中国电建集团华东勘测设计研究院有限公司，浙江杭州311122)

1 研究背景

近年来，随着数值计算水平地不断发展，水电站厂房结构在脉动压力作用下的振动响应数值分析逐渐被相关学者关注，文献[1]对比了脉动压力谐响应分析和时程分析两种计算方法的差异性，认为能够获得脉动压力时程资料时，应尽量采用时程分析法计算动力响应；文献[2]针对不同频域的脉动压力对厂房结构振动的影响进行了研究；文献[3- 4]基于功率流理论和功率流有限元方法研究了脉动压力作用下结构的响应；文献[5]基于流固耦合界面数据传递模型研究了水电站厂房流激振动，认为水轮机叶片与导叶间静动干扰所引起的流体脉动压力对厂房整体结构振动影响较为明显。综上，已有研究成果主要集中在采用不同方法研究水电站厂房结构的动力响应，如谐响应分析、时程分析、功率流有限元方法、流固耦合等，在计算分析中没有对结构自身阻尼方面做研究。然而，阻尼是结构动力计算分析中不可忽视的重要参数，其自身是较为复杂的问题[6-11]。结构的阻尼耗能主要是摩擦耗能，结构不同振型下的层间相对位移有差异，摩擦耗能也不同，故而每个振型下的阻尼比是不同的。目前常用的比例阻尼模型有 柯西阻尼模型、克拉夫阻尼模型、董军阻尼模型和Rayleigh阻尼模型等[9-10]。

Rayleigh阻尼模型是结构动力分析中最常用的模型，其物理关系明确，计算简单，因而得到广泛应用；Rayleigh阻尼模型表达式为

[C]=α0[M]+α1[K]

(1)

式中，[C]为阻尼矩阵；[M]为结构体系的质量矩阵；[K]为结构体系的刚度矩阵；α0和α1为阻尼系数，α0和α1与振型阻尼比之间关系为

(2)

式中，ξk为第k阶振型的阻尼比；ωk为第k阶振型的频率。给定两个振型阻尼比即可确定阻尼系数α0和α1。

阻尼比对Rayleigh阻尼模型的阻尼系数的取值有直接影响，而阻尼比的影响因素较多，目前各国抗震设计规范根据本国研究成果和参考他国资料，按照结构类型等给出了建议的阻尼比值[8]。我国GB50011—2010《建筑物抗震设计规范》[12]中明确除有专门规定外，建筑结构的阻尼比应取0.05；NB35047—2015《水电工程水工建筑物抗震设计规范》[13]中规定各类水工建筑物的阻尼比取值为：土石坝可取为20%，拱坝可取为5%，重力坝可取为10%，水闸、进水塔及其他建筑物可取为7%。

本文借鉴已有的相关研究成果，基于大型有限元计算程序ANSYS，采用Rayleigh阻尼模型，针对不同的阻尼比取值，研究阻尼比对水电站厂房结构在脉动压力荷载作用下响应的影响。

2 计算模型及荷载

本文以某抽水蓄能电站地下厂房为例，电站装机容量为1 200 MW(4×300 MW)，安装4台单机容量为300 MW的混流可逆式水泵水轮发动机组，机组额定转速500 r/min。机组段上下游及左右侧均采用3跨4柱的布置方式，柱断面尺寸1.0 m×1.0 m；发电机层楼板厚60 cm，中间层与水轮机层厚为50 cm；主梁断面尺寸为0.8 m×1.5 m，次梁断面尺寸为0.6 m×1.2 m。

本文以机组段为对象开展计算分析，采用ANSYS建模计算。沿厂房纵轴线方向取的长度为22.50 m，宽度为21.80 m，高度上取尾水管开挖底板高程至发电机层楼面高程，总高度为27.85 m。计算模型中X轴为水平方向，沿厂房纵轴指向左端为正(面向下游)，Y轴为铅垂方向，向上为正；Z轴为水平方向，指向下游为正；坐标系原点取在机组安装高程处。厂房结构的三维有限元模型见图1。

水轮机脉动压力试验共布置9个测点，包括蜗壳进口1个测点、无翼区2个测点、顶盖与转轮上冠之间1个测点、底环与转轮下环之间1个测点、尾水锥管2个测点、尾水肘管2个测点。每个测点均布置一个动态压力传感器。为便于计算，将流道分为5个区域进行加载，如图2所示；计算采用对应于原型水头539.09 m，原型出力接近额定出力300 MW的各测点实测的脉动压力数据，例如③区的脉动压力时程曲线如图3所示。

图1 厂房结构三维有限元模型

图2 流道加载分区

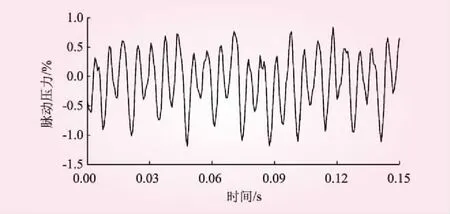
图3 ③区脉动压力时程曲线

3 阻尼比对厂房结构响应的影响分析

阻尼比是结构动力计算中的重要参数之一，为满足数值计算成果的完整性，本文选取了6组阻尼比进行对比分析，即ξ=0.000 1，0.02，0.04，0.06，0.08，0.1。计算结果见图4～6及表1。

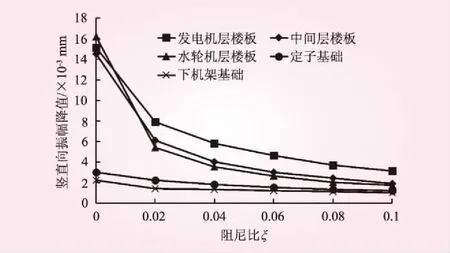
图4 竖直向振幅峰值随阻尼比变化

图5 竖直向振动速度峰值随阻尼比变化

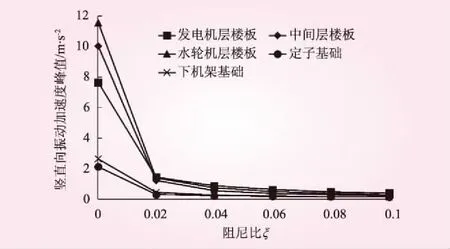
图6 竖直向振动加速度峰值随阻尼比变化

根据计算结果，阻尼比ξ在0.02～0.1范围时，厂房结构的振动响应随着阻尼比的增大而减小，说明阻尼的存在有助于减弱结构的振动。此外，厂房结构振动响应规律基本是一致的，在流道内脉动压力作用下，上部典型部位的竖直向振幅、振动速度、振动加速度均呈现随着高程的增加而有增大的趋势。本工程厂房结构随高程的增加，其质量和刚度是逐

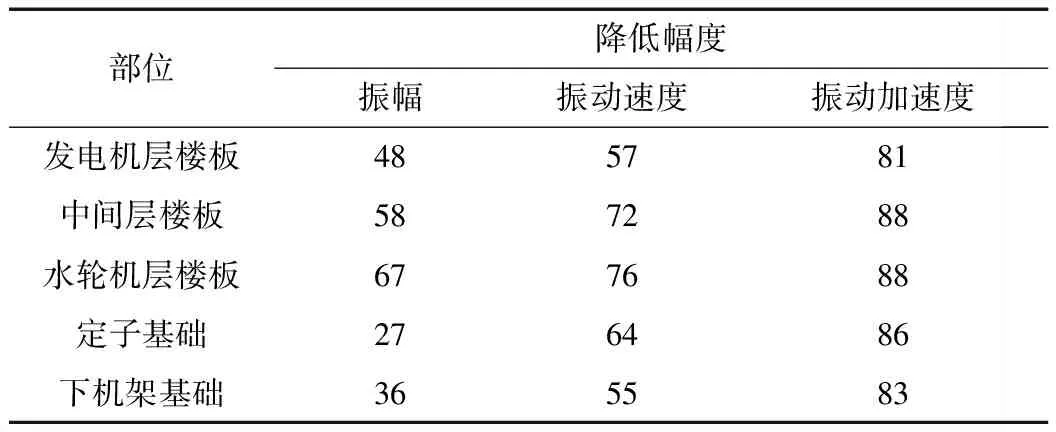
表1 典型部位竖直向响应幅值降低幅度( ξ=0.02相较于 ξ=0.000 1) %

渐减小的，从而导致在流道内脉动压力作用下，高高程部位的结构易形成相对较大速度和振幅，即有一定的“鞭梢效应”存在。

通过比较可知，阻尼比ξ=0.000 1时(即基本不考虑结构阻尼)，厂房结构的竖直向振幅、振动速度、振动加速度响应值均远大于阻尼比ξ在0.02～0.1范围时的厂房结构响应。ξ=0.02相对于ξ=0.000 1而言，结构的竖直向振幅峰值降幅在27%～67%，竖直向振动速度峰值降幅在55%～76%，竖直向振动加速度峰值降幅在81%～88%。除此之外，基本不考虑结构阻尼时，结构典型部位的最大响应出现在水轮机层楼板，即靠近脉动压力激振的部位响应更明显，“鞭梢效应”没有体现出来。

由以上分析可知，在水电站厂房结构脉动压力数值计算时须考虑结构阻尼的影响，阻尼比的大小对结构响应影响明显，应当根据结构特点合理取值。

4 人体舒适度评价

在一定条件下，振动强度达到一定程度时，会引起人的不良感觉，进而对心理和生理产生影响，甚至危害人体健康，振动强度一般用加速度的有效值表示。除了强度之外，还有两个十分重要的因素，一是振动的频率，二是承受振动的时间。试验证明，人对频率在4～8 Hz的振动最为敏感。由于目前国内没有专门针对水电站厂房的人体舒适度评价标准，本文参考GB/T 13441.1—2007《机械振动与冲击 人体暴露于全身振动的评价 第1部分：一般要求》[14]对人体在公共交通中综合振动总值的不同量值可能反应的近似描述，对人体舒适度做评价分析。

GB/T13441.1—2007中有关人体舒适度的控制标准描述如下：综合振动总值小于0.315 m/s2，感觉不到不舒适；综合振动总值在0.315～0.63 m/s2时，有点不舒适；综合振动总值在0.5～1 m/s2时，相当不舒适；综合振动总值在0.8～1.6 m/s2时，不舒适；综合振动总值在1.25～2.5 m/s2时，非常不舒适；综合振动总值大于2 m/s2时，极不舒适。

以发电机层楼板特征点为例，对其在不同阻尼比下的振动加速度曲线进行频谱分析[15]，即对加速度时程曲线进行傅里叶变换得到FFT频谱。表2给出了发电机层楼板特征点在不同阻尼比下的均方根加速度值及主频，主频对应的计权系数可根据GB/T 13441.1—2007中表3查到。

表2 发电机层楼板特征点均方根加速度及其主频

注：表中竖直向综合振动值=均方根加速度×计权系数。

由表2可知，发电机层楼板特征点的均方根加速度随着阻尼比的增大而减小，这与上一小节的分析一致；不同阻尼比下的发电机层楼板加速度的主频均为3.67 Hz，频率较低，处在人体较敏感频率附近；阻尼比为0.000 1、0.02、0.04时，人体舒适反应描述分别为不舒适、相当不舒适、有点不舒适，阻尼比为0.06～0.10时，人体人体舒适反应描述为感觉不到不舒适。由此可知，阻尼比的取值对人体舒适度评价有较大影响，不考虑结构阻尼存在时，综合振动值偏大，水电站厂房结构脉动压力数值计算时须考虑结构阻尼的影响。

需要说明的是本文计算的时长仅有0.15 s，若时长增加，输入的实测脉动压力的频谱可能会出现变化，相应计算输出的结构响应频谱也会变化，因此表2中的综合振动值不代表完整脉动压力时长下的结构响应，但可以用来反应阻尼比对结构响应的影响规律。

5 结 论

(1)结构阻尼是结构在受到振动作用时自身固有特性，不考虑阻尼影响会导致计算结果偏危险，因此，水电站厂房结构脉动压力数值计算时须考虑结构阻尼的影响。

(2)采用Rayleigh阻尼模型，阻尼比对水电站厂房结构脉动压力数值计算结果影响较大，结构振动响应随着阻尼的增大而减小；对于水电站厂房结构而言，目前规范建议的阻尼比5%～7%是基于一定的研究成果基础上取得的，数值计算采用ξ=5%～7%是合理的。

(3)本文计算采用的是固定阻尼比，实际上不同振型下结构的阻尼比是有差异的，针对数值计算分析中的如何考虑随结构振型阶数增加而阻尼比增加的情况仍需继续研究，以期更好地反应结构的实际响应。