强震作用下反倾层状岩质边坡变形及破坏模式研究

刘汉东，耿 正，王忠福，牛林峰，王四巍，徐 峰

(1.华北水利水电大学岩土力学与水工结构研究院，河南郑州450045；2.河南省岩土力学与结构工程重点实验室，河南郑州450045；3.黄河勘测规划设计研究院有限公司，河南郑州450003)

0 引 言

地震诱发边坡失稳造成人员伤亡和财产损失，影响重大工程建设，破坏生态环境。据统计，“5·12”汶川地震诱发滑坡造成的次生灾害损失占整个地震灾害直接损失的约1/3[1]。地震作用下的边坡稳定性问题已经成为学科研究的热点[2-5]。了解地震作用下边坡变形破坏模式是对边坡失稳预报和防治的前提[6]。

许多学者对地震诱发边坡变形破坏模式进行了探讨[7-9]。董金玉等[10]通过振动台试验对顺层岩质边坡的破坏模式进行了研究，得到该类边坡的破坏模式为地震诱发—坡肩拉裂张开—坡面中部出现裂缝—裂缝贯通—发生高位滑坡—转化为碎屑流—堆积坡脚；邹威等[11]对不同岩性组合水平层状岩质边坡进行了大型振动台模型试验研究，将水平层状岩质边坡变形破坏成因模式归纳为拉裂—剪切—水平滑移型和拉裂—剪切—散体崩落型；Wang J等[12]通过对典型黄土回填边坡进行监测发现，该类边坡的破坏模式为裂缝的发展—压实黄土的软化—斜坡前缘的蠕变和后缘的裂缝—贯穿滑动面的形成。

尽管目前在地震诱发边坡变形破坏模式方面取得了丰硕成果，但对强震作用下反倾层状岩质边坡的变形破坏模式方面却少有研究。为此，本文参考国内外研究成果，建立了反倾层状岩质边坡的概化模型，通过振动台模型试验得到了反倾层状岩质边坡在强震作用下的变形规律和破坏模式，通过有限差分法对试验结果进行了验证。研究成果可为地震条件下反倾层状岩质边坡失稳预报及防治提供参考。

1 振动台模型试验设计及数值模型的建立

1.1 模型相似比的确定

根据相似理论，以长度、密度、弹性模量为主控因素，将其相似常数设置分别为Sl=60、Sρ=3、SE=100。按照Buckingham π[13]定理，推导出其他相似常数。模型试验相似比设计见表1。

表1 模型试验相似比设计

1.2 模型试验装置及材料参数

振动台模型由模块堆积而成，模块由水和石膏按1∶0.8的配合比制作而成，其物理力学参数见表2。模块尺寸为12 cm×6 cm×2 cm(长×宽×高)。模块间用浓度为40%的白乳胶粘结，其内摩擦角为30. 6°，粘聚力为115. 36 kPa。边坡模型长0.60 m，高0.60 m，厚0.12 m，见图1。边坡后缘设置5个加速度传感器(D1～D5)，传感器布置见图2。为便于描述加速度峰值大小，将边坡上监测点的动力响应加速度峰值与边坡底部D1点的加速度峰值的比值定义为PGA(Peak Ground Acceleration)放大系数。

表2 试验材料物理力学参数

图1 边坡模型

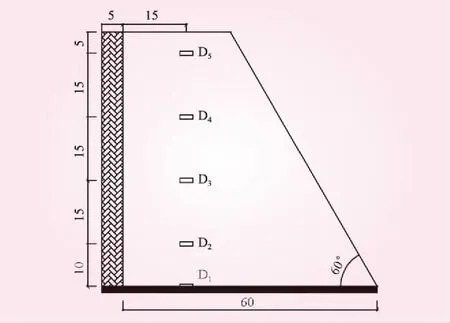
图2 监测点布置(单位：cm)

1.3 数值计算条件

参考室内振动台模型试验边坡的原型，设置模型高为36 m，底部边长为34 m，边坡坡角60°，岩层倾角75°，岩层厚度1.1 m，软弱夹层厚度0.1 m。计算模型及网格划分见图3。共计2 762个单元，3 562个节点。将岩石及结构面材料设置为弹塑性材料，服从Mohr-Coulomb屈服准则。岩石及结构面物理力学参数见表3。

图3 数值计算模型

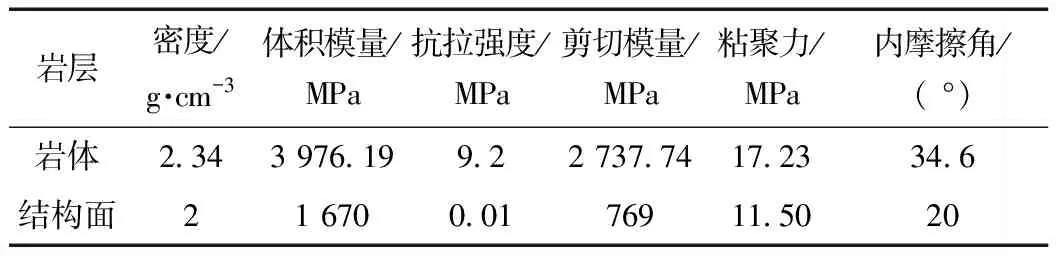
表3 岩体及结构面物理力学参数

本文研究对象为反倾层状岩质边坡，基岩弹性模量较大，属于刚性地基，因此模型底部不设置静态边界条件，模型四周为自由场边界。

在坡体内部距边坡后缘10 m处竖直方向上，在边坡底部、距边坡底部6、15、24 m和33 m处设置监测点(A1～A5)，与室内试验布置的监测点(D1～D5)相对应，边界条件和监测点布置见图4。

在模型底部设置加速度监测点，与输入的加速度时程曲线进行对比，结果证明2条曲线基本无差异，说明地震波输入正确。为了验证边界条件的正确性，在模型左侧和右侧边界设置了监测点，监测其加速度，结果证明边界模拟效果良好，2条加速度时程曲线无明显差异。

图4 监测点布设及边界条件

1.4 数值模拟的试验验证

为验证数值模拟的合理性，设计频率为5 Hz、震动强度为0.1g和频率为5 Hz、震动强度为0.2g这2种工况进行室内振动台试验，并对其进行数值模拟，将得到的结果进行对比。室内试验中的加速度传感器D1～D5分别与模拟工况的A1～A5这5个监测点对应，分别求出其PGA放大系数进行对比。室内试验与数值模拟结果对比见图5。

图5 数值模拟与室内试验结果对比

从图5可以看出，模拟结果较试验结果偏大，这是由于数值模拟的条件更为理想化，室内试验有很多影响因素，如振动台与模型底部的摩擦力，部分坡体间粘结不太均匀等，在数值模拟工况中并没有考虑。但数值计算和模型试验结果总体规律是一致的，说明数值模拟与室内试验吻合较好，结果可信。

2 结果及分析

2.1 室内试验

室内模型试验采用峰值加速度为2g、频率为20 Hz的正弦波进行加载。振动台试验不同时刻边坡破坏情形见图6。从图6可知，t=5 s时，边坡模型的坡面中部浅层岩体发生破坏，且伴有零星掉块现象；t=10 s时，边坡模型中下部拉张裂缝开始发育，但并不明显；t=15 s时，边坡模型中下部拉张裂缝的发育明显，且开始向边坡内部发展；t=20 s时，部分岩体开始向临空面方向剪出；t=25 s时，边坡模型中下部岩体开始大面积向临空面方向剪出；t=30 s时，边坡模型出现大面积垮塌现象，边坡上部岩体出现向临空面弯曲现象。

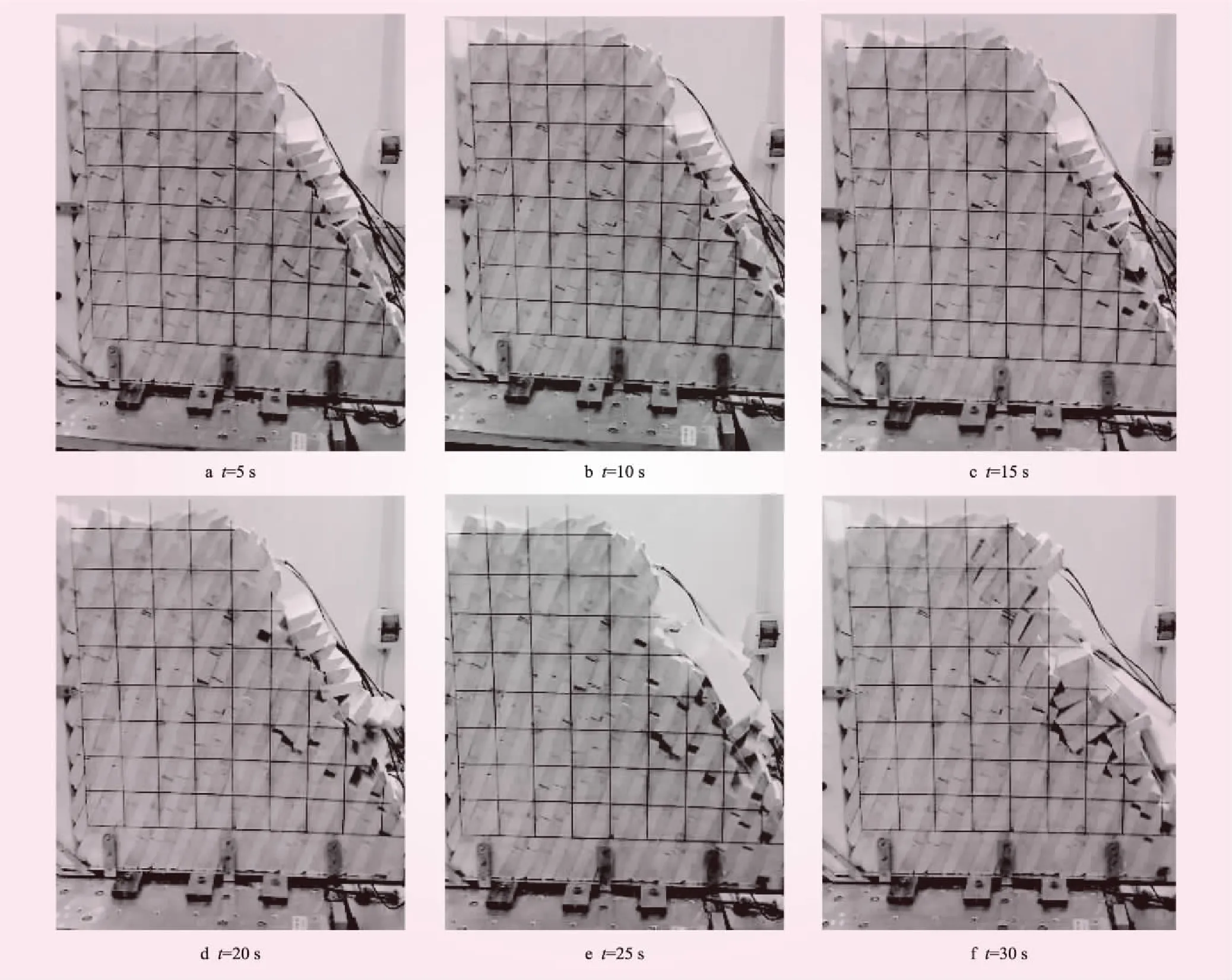
图6 振动台试验不同时刻边坡破坏情形

通过室内试验可以看出，输入高频率、大振幅的横向正弦波，反倾层状岩质边坡破坏初期主要为坡面中部浅表部的岩体松动，出现零星掉块现象，此时边坡并未发生整体失稳。边坡整体失稳是由于裂隙发展、延伸并逐渐贯通，最终引起边坡发生大面积的崩塌破坏。裂隙从边坡的中下部开始发育，沿结构面不断向内部和上部延伸，同时，由于震动的持续，边坡内部岩体发生错动，并向临空面方向剪出，最终裂隙贯通，导致边坡的整体失稳。

通过对试验不同阶段破坏模式进行分析，可将反倾层状岩质边坡的变形破坏分为以下3个阶段：

(1)坡面浅表部松动，裂隙产生阶段。在震动初期，边坡的变形破坏主要发生在坡面的浅表部，表现为松动和掉块现象；随着震动的持续，边坡中下部开始出现拉张裂缝，地震产生的应力波在结构面处相互叠加，产生拉应力，是裂缝产生的重要原因[14]。

(2)裂隙延伸，岩体错动阶段。持续的震动导致裂隙沿结构面向边坡内部和上部延伸并扩张，且坡体内部岩体的错动不断加剧，并向临空面方向剪出，部分岩体出现脱层现象。

(3)裂隙贯通，边坡大面积垮塌。裂隙的扩展及岩体的错动形成贯通的结构面，导致边坡大面积崩塌，破坏面呈阶梯状，崩塌部分上部岩体向临空面方向弯曲，虽然并未掉落，但裂隙已经开裂，形成危岩体，若震后受到外部荷载作用，则可能发生破坏[15]。

2.2 数值模拟

采用FLAC3D软件对室内模型试验进行模拟。根据相似比确定输入的地震波的加速度为1.2g，频率为20 Hz，模拟结果见图7。从图7可以看出，当t=5、10、15、20、25 s和30 s时，模型最大位移量分别为1.27、2.71、4.16、5.63、7.09 mm和8.56 mm。模型的形变量随着时间的增加而逐渐增大。

图7 数值模拟不同时刻边坡位移云图

由模拟结果可知，在输入高频率、大振幅的横向正弦波时，模型的最大位移处在坡面中部，其次为边坡顶部、坡肩及坡脚处，模型最小位移处在边坡后部和底部，位移量从边坡中部向边坡后部和底部依次递减，这与室内试验边坡破坏规律近似一致。地震波持时也对反倾层状岩质边坡的失稳具有很大影响[16]，即随着震动的持续，边坡各部分的位移持续增大[17]，但其分布规律基本不变。

3 结 语

本文通过振动台试验和数值分析，研究了强震作用下反倾层状岩质边坡的变形破坏模式及变形规律，得到如下结论：

(1)地震波持时对反倾层状岩质边坡失稳有很大影响，主要表现在坡体的位移不断增大，坡内能量不断累积，裂隙不断发育发展。

(2)裂隙的产生、发育和贯通是导致反倾层状岩质边坡整体失稳的主要原因。裂隙从边坡的中下部开始发育，沿结构面不断向边坡内部和上部延伸，最终贯通，导致边坡大面积崩塌破坏。

(3)在输入高频率、大振幅的水平向正弦波的情况下，反倾层状岩质边坡的破坏模式为：坡面浅表部松动，开始产生裂隙，并持续发育，不断向坡体内部及上部延伸，坡体内部发生岩体错动并不断加剧，直至裂隙贯通，边坡大面积崩塌破坏。

(4)强震作用下，反倾层状岩质边坡的主要变形规律为：在震动初期，坡表部分岩体松动，最终脱离坡体形成坠落；随着震动的持续，裂隙沿坡体内部结构面逐渐贯通，形成崩塌；崩塌产生后，崩塌处上部部分岩体向临空面弯曲形成危岩体。