多波次导弹发射路径规划

章 胤, 田子豪, 张 顺, 于 溪, 赵士贤

(1.燕山大学 理学院， 河北 秦皇岛 066004;2.燕山大学 信息科学与工程学院， 河北 秦皇岛 066004)

0 引 言

导弹武器以其射程远、精度高、威力大等诸多优点成为打击敌方军事要地，以及政治中心和重要设施的主要手段之一。多波次、大弹量的常规导弹打击涉及到导弹的机动运输。如何设计较优的机动路径，使导弹发射装置以最短的时间机动至相应阵地，从而减少暴露时间、增加生存概率显得至关重要[1]。文中使用遗传算法针对一般的机动规划模型做出了改进[2]。为了提高遗传算法的收敛性，文中改进了基本的交叉、变异算子，并采取基于收敛程度变异概率的方法，保证该算法应对突发状况时不会产生错误的信息。

1 机动模型的建立

对于多波次导弹的发射问题，其基本流程为：导弹发射装置从待机地域前往第1波次发射点位；然后在其第1波次齐射完毕后，发射装置前往转载地域；接着发射装置从转载地域出发前往第2波次发射点，直至最后一个波次导弹发射完毕。其中每一次发射点位不能和上一次发射点位相同，以免因发射点位暴露而遭到敌人的打击。由于发射装置在第2波次及之后的发射过程与之前的发射过程完全相同，因此在接下来分析过程中，首先研究两个波次的导弹发射过程，再将其扩展到多波次发射。

该模型主要实现发射装置在两波次导弹发射过程中的暴露时间最短，由此得出目标函数

minT=mint1+mint2，

(1)

式中：minT——两波次发射的最短暴露时间;

mint1——导弹发射装置从待机地域到第1次发射点位的时间;

mint2——导弹发射装置从第1次发射点位到转载地域，并从转载地域到第2次发射点位的时间和。

两个波次导弹发射的三段路径约束(车辆数为K)如下：

1)从待机地域前往第1次发射点准备齐射。

每个发射点位不能重复使用

(2)

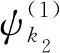
每辆车载装置的始发地和目的地不能相同

(3)

导弹车载装置从待机区域到第1次发射点位所需时间

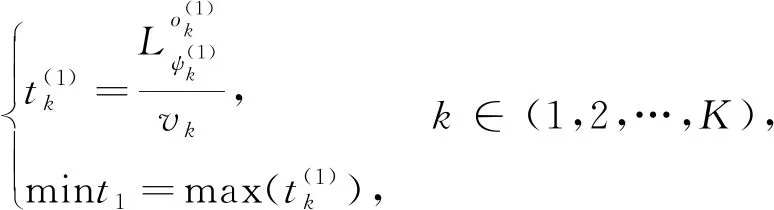
(4)

式中：vk——第k辆车载装置的速度;

2)从发射点到达转载地域装弹。

出发点为第1次发射点位，目的地为转载地域

(5)

每个装载地域同时只能一辆车装弹,且装弹时间为10 min

(6)

导弹车载装置从第1次发射点出发到装弹地域的时间

(7)

3)从转载地域到达第2波次发射点。

(8)

车载装置从导弹装载地域机动至第2次发射点位所需时间

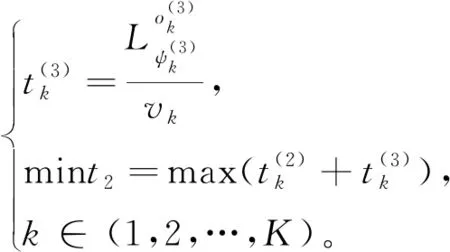
(9)

2 算法设计

2.1 数据预处理

使用ArcMap构建交通路网图，并用其线段距离计算功能计算各相邻结点间欧氏距离[3]。运用Dijkstra算法求解待机地域到发射点位和转载地域到发射点位之间的最短距离[4]。

2.2 遗传算法设计

2.2.1 确定染色体结构

采用整数编码方式[5],每一辆车载装置两波次间发射经历三个过程，故将每条染色体分为三段,每段的基因数等于车辆数，如图1所示。

图1 染色体编码

2.2.2 算法的具体步骤[6]

2.2.2.1 种群初始化

初始化函数采用随机生成法,保证式(1)和式(7)的约束成立。

2.2.2.2 选择

采取随机抽样选择的方法，依据高适应度优先选择的原则，从群体中选择优良个体，用以繁殖到下一代个体。

2.2.2.3 交叉

每次从种群中随机选择两条染色体进行交叉组合，而后随机选择进行交叉操作的染色体基因。根据构造的染色体结构，将转载区和发射区分别进行交叉操作。当发射点基因段进行交叉时，首先判断需要交叉的发射点是否与本染色体的发射点基因重复，如果重复，则重新进行交叉操作。

2.2.2.4 变异

从种群中随机选择一个个体进行变异。当需要对发射点位进行变异时，首先判断要变异的发射点位是否重复，如果重复，则重新进行变异操作。考虑到每条染色体基因数目较多，在变异操作时将发射点位与转载地域的染色体变异分开进行。

2.2.3 算法的改进

2.2.3.1 多点交叉

当种群出现“早熟”现象[7]时，考虑对染色体进行多点随机交叉，即对两条染色体进行多基因交叉,对同一类基因进行跨位置交叉的过程。以此提高催生新的个体的速率，从而加快寻优速率。交叉点个数由基因长度决定，基因越长，选取的交叉点个数越多。染色体多点交叉具体过程如图2所示。

2.2.3.2 提高收敛种群的变异概率

当种群出现“早熟”现象[7]时，可通过增大这些拥有相同基因的染色体的变异概率,概率数值为正常个体变异概率的3～4倍,从而使新的种群中拥有更多不同的染色体,促生新的染色体的出现,提高全局寻优速率。

图2 染色体多点交叉示意图

3 算例结果及分析

对于24台导弹发射装置、60个发射点位、6个转载地域使用MATLAB编程多次求解得出发射装置机动路线方案，统计两波导弹发射总耗时数据见表1。

表1 导弹发射装置的机动路线方案

从表1中选取暴露时间最短的一组数据整理出机动路线方案见表2。

表2 导弹发射装置的机动路线方案

使用Excel软件统计分析表2中的数据可知，两个波次的导弹发射一共耗时约为498.6 min(8.31 h)。

使用ArcMap工具软件，将道路交通网络构成网络数据集，绘制所有发射装置的机动路线。A01发射装置的机动路线如3所示。

图3 A01发射装置机动路线图

图3中,D1-Z03-J57-J58-J59-J62-F60代表发射装置从待机地域出发到第1次发射点位的机动路线；F60-J62-J59-J58-J57-Z03-J52-J07-Z04代表发射装置从第1波次发射点位行驶至转载地域进行装弹的机动路线；Z04-J38-F34代表发射装置从转载地域出发到第2波次发射点位的机动路线。

4 结 语

确立了多步骤单次行动最短的路径模型，将多波次的导弹发射过程看作重要节点间的移动，而每个单次发射过程之间的细节采用Dijkstra所求得的时间路径[8]得出，从而构造了一种基于Dijkstra算法和遗传算法的路径优化求解模型。在针对两个波次导弹发射的实例中，文中的Dijkstra算法和遗传算法的路径优化模型得到了整体暴露时间为490～520 min，相比单独的Dijkstra算法550 min的结果，最短暴露时间缩短了7%～10%。