基于迭代随机森林算法的糖尿病预测

刘文博, 梁盛楠, 秦喜文, 董小刚*, 王纯杰

(1.黔南民族师范学院 数学与统计学院， 贵州 都匀 558000;2.长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

糖尿病是一组以高血糖为特征的代谢性疾病，高血糖是由于胰岛素分泌、胰岛素作用缺陷或两者兼而有之所致[1]，其中，Ⅱ型糖尿病是最为常见的类型，约占糖尿病患者总数的90%，该类糖尿病是由于胰岛素抵抗致使进行性胰岛素分泌缺陷[2]。糖尿病的发病率和患病率正在呈现出逐年上升且低龄化的趋势，已成为我国乃至世界的重大公共健康安全问题[3]。由于多数患者意识不到糖尿病患病前期出现的症状，以致最终发展为糖尿病。若在发病前的潜伏期及早地对糖尿病风险进行有效干预，每年大约有6%～10%的患者不会发展为糖尿病[4]。故对糖尿病进行有效预防和检测是一项至关重要的工作，进行干预的实质就是要尽早地发现糖尿病风险。

传统的诊断依据主要是通过检测餐后血糖和糖化血红蛋白,进而对糖尿病进行评估，尽管十分精确但成本较高[5]；另一方面将医生积累多年的个人经验作为重要参考，随着诊断数量的增加和疲劳感上升，时常会出现误诊或漏诊现象。为了有效解决传统诊疗方式的弊端，减少治疗成本，提高糖尿病预测的精度，近年来，基于机器学习算法的各种分类器系统在糖尿病、乳腺癌等医学诊断中的应用逐渐增多。

Smith等[6]使用Logistic回归和ADAP方法对皮玛族印第安女性糖尿病数据集(Pima Indians Women Diabetes)进行分类预测，得到相应的精度分别为79.17%和76%;Stern等[7]通过预测7.5 a的Ⅱ型糖尿病发病率，验证了与单纯依赖2 h口服糖耐量试验结果相比，使用多元Logistic回归模型可更好地识别糖尿病高危人群;Raymer等[8]利用Naïve Bayes 和Nonlinear Bayes分类器对皮玛族印第安女性糖尿病数据集进行分类研究，在测试集上的分类精度分别为64.6%和70.4%;Eggermont等[9]利用C4.5和Bagged C4.5算法对皮玛族印第安女性糖尿病数据集进行分类预测，获得的分类精度分别为71.6%和75.6%。

以往研究结果表明，与其它类型的糖尿病数据集相比较，皮玛族印第安女性糖尿病数据是一类比较难分的数据集，体现在多数分类算法对其分类时得到的分类精度不高，最差时仅有60%左右。应从更好的检测特征间交互作用的角度，来提高Pima数据集的分类精度。当下很多机器学习方法尽管可以检测特征间的交互作用，但并没有考虑到不影响预测精度的前提下去检测“高阶交互作用”，诸如CART[10]，Node Harvest[11]，Forest Garrote[12]，Rulefit3[13]和Bayesian epistasis mapping[14]。

为了克服上述算法的缺点，在随机森林(RF)、随机交叉树(RITs)的基础上，通过广泛的生物模拟，Basu等[15]开发了迭代随机森林算法(Iterative Random Forests， IRF)，IRF训练一个特征加权的决策树集合来检测稳定、高阶的交互作用，其计算代价与RF相同。鉴于此，文中提出一种可识别高阶交互作用的迭代随机森林算法,应用于Pima糖尿病数据集的分类预测研究。

1 迭代随机森林

1.1 随机森林

随机森林(Random Forest)是由Breiman[16]提出的，其基本原理为：对原始数据集做多次有放回抽样(Bootstrap)，每次抽取的样本容量与原始数据相同，由于是“有放回”,所以总会有一些数据被重复抽取,而另外一些根本就没被抽取到，由公式(1-1/N)N≈1/e可知，没抽到样本约占原始数据集的37%，如此就会得到许多不同的数据集；然后对每个数据集建立一个决策树(Decision Tree)，对于随机森林中每棵树的每个节点，变量的拆分不是由所有变量竞争，而是由“随机挑选”的少数变量竞争，且每棵树都长到底，这样可以避免由于强势变量的主宰而忽略数据关系中的细节，极大地提高了模型对数据的代表性；最后，对于一个新的观测值，通过n棵树得到n个预测结果，对于回归问题取这n个预测值的平均作为最终预测结果，而对于分类问题，采取“少数服从多数原则”，即n个预测中出现最多的类作为最终预测类。

1.2 迭代随机森林

迭代随机森林的基本思想是在随机森林的基础上通过对选定的特征进行“迭代重新赋权”(Iterative Re-weighting)得到一个带有特征权重的随机森林[17]，然后利用泛化的随机交叉树[18]作用于带有特征权重的随机森林上，进而识别出特征的高阶交互作用,同时能够保证迭代随机森林也有很好的预测能力，至少与随机森林不相上下。

迭代随机森林的具体工作流程主要为以下三步[19]：

2)泛化的随机交叉树作用于RF(ωK)，其中RF(ωK)为第K次迭代产生的具有特征权重的随机森林，本步骤产生了一组交叉作用集S。

3)Bagged稳定得分，我们使用“外层”(Out Layer)自助法用以评价重现交叉作用的稳定性，生成自助抽样的数据集D(b),b=1,2,…,B，在每一数据集D(b)上拟合随机森林RF(ωK)，并且在每一个自助抽样集上使用泛化随机交叉树来识别交互作用集S(b)，给出交叉作用集S的稳定分数公式

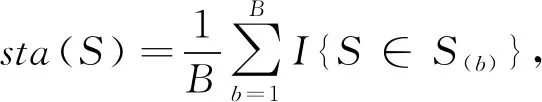
(1)

1.3 分类模型的性能指标

为了比较不同分类模型的优劣，需要给出评价模型性能的度量指标，以最常见的二分类问题为例给出相应的模型评价指标。在二分类问题中，可将样本根据真实类和分类模型给出的预测类的组合，划分为真正例(True Positive， TP)、假正例(False Positive， FP)、真反例(True Negative， TN)、假反例(False Negative， FN)四种情况[21]，令TP、FP、TN、FN分别表示对应的样本数，易见TP+FP+TN+FN=n，其中n为样本容量，分类结果的混淆矩阵(Confusion Matrix)见表1。

表1 二分类问题预测结果的混淆矩阵

分类精度(Accuracy)、查准率(Precision)和查全率(Recall)分别定义为:

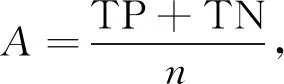
(2)

(3)

(4)

尽管分类精度可以从总体上较好地刻画分类模型的分类性能，但有时并不能满足所有的任务需求。以医学诊断为例，分类精度表明有多少比例的就诊人数被正确归类(患病、无病)，但是往往我们更关心“被诊断为患病的人群中有多少比例的人确实患病”或“在所有患病人群中有多少比例的人被诊断为患病”，显然精度就无法进行衡量了，这就需要借助于式(3)和式(4)的P和R来进行度量。需要指出的是P和R是一对相互矛盾的度量，即其中一个量增大,另外一个量往往减少。

有时需要综合P和R去度量一个分类器的好坏，而不是仅就P和R某单一指标去评价分类模型，更为常用的是F1度量

(5)

等价的可表示为

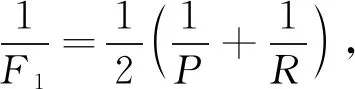
(6)

式中：F1——基于P和R的调和平均。

2 实证分析

2.1 数据来源与探索性分析

文中研究数据来自于美国国家糖尿病消化病肾病研究所，该数据集提供了亚利桑那州中南部皮玛族印第安后裔成年女性(年龄在21岁以上)的糖尿病诊断信息，共786个观测样本，其中268例被诊断为糖尿病阳性，500例为糖尿病阴性。提取的多项相关糖尿病危险因素分别为怀孕次数(npreg)、血糖浓度(glu)、舒张压(bp)、三头肌皮褶厚度(skin)、血清胰岛素(insulin)、身体质量指数(bmi)、糖尿病家族影响因素(ped)、年龄(age)，同时还提取了一个类别标签，未来5年是否会患有糖尿病(type，1代表是，0代表否)。按照世界卫生组织的标准进行诊断，数据集中包含的患者为Ⅱ型糖尿病，即“非胰岛素依赖型”糖尿病。

为了解数据集取值基本情况，给出数据集中的部分样本观测值，见表2。

表2 皮玛族成年女性糖尿病诊断信息

为了进一步了解属性特征对患病类别的影响以及数据的分布状况，对数据集进行基本的探索性分析，给出数据集所有属性特征对类别标签的箱线图,如图1所示。

图1 皮玛族印第安成年女性糖尿病数据集在类别标签下属性特征取值的分布状况

由于各个属性特征单位不尽相同，需要对数据集进行标准化处理,即转换均值为0、标准差为1的形式，进而生成更有意义的统计图形。图1给出了每个类别下各个属性特征的取值分布状况，例如患有糖尿病的人群身体质量指数(bmi)、年龄(age)、血糖浓度(glu)明显要高于非患病人群。由于血清胰岛素是人体内降低血糖的主要激素，糖尿病患者体内血清胰岛素含量应低于正常人群，从图1中可以看出，在所有特征中只有血清胰岛素(insulin)这一项因素在糖尿病人群中要低于非患病人群，符合实际情形。

接下来，基于迭代随机森林对影响糖尿病发展程度的属性变量做重要性分析，探索出哪些特征对算法的分类精度会产生主要影响，得到相应的变量重要性排序结果如图2所示。

图2(a)是利用“袋外数据”(Out of Bag)作为训练集所做的交叉验证得到的度量，表示删除某个自变量后平均减少的精度，减少的越多说明变量越重要，按照平均减少的精度进行变量重要性从大到小排序可得glu、bmi、age、npreg、insulin、ped、skin、bp；图2(b)为综合了每个自变量在各个节点的表现而产生的重要性度量(使得数据变“纯”,即分支节点所包含的样本尽可能属于同一类)，表示删除某个变量后平均减少的基尼指数[22]，减少的越多说明变量越重要，按照基尼指数的减少程度对变量的重要性从大到小进行排序可得glu、bmi、age、ped、bp、npreg、insulin、skin。从排序结果可以看出，无论按照哪种衡量标准对变量的重要程度排序，对是否患有糖尿病影响最深的三个变量都是血糖浓度、身体质量指数和年龄，说明血糖浓度过高、肥胖、年龄偏大的人群更易患有糖尿病。所以在糖尿病的预防工作中，应对血糖浓度和身体质量指数这两项指标应加以控制。

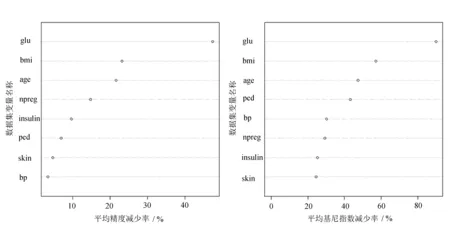
(a) 数据集平均精度减少率 (b) 数据集平均基尼指数减少率

图2 基于迭代随机森林的皮玛族糖尿病数据集8项属性特征重要性分析

2.2 迭代随机森林Ⅱ型糖尿病分类

为了进一步提高糖尿病数据集的分类精度，即能够对糖尿病患者与非患者进行正确识别，提出一种“可识别高阶交互作用的迭代随机森林算法”，针对皮玛族成年女性是否患有糖尿病进行判别分类研究。文中所建立的分类预测模型是在Windows7,64位操作系统下实现的，采用的开发平台是R*64 3.5.0，硬件为i3-2310M CPU 2.10 GHz，4 G内存。

首先，通过Bootstrap随机抽样把数据集分为训练集和测试集。在利用迭代随机森林进行分类时，需要设置迭代次数，为了比较不同次数是否会产生不同的分类效果，设置迭代次数为8次，基于测试集各个迭代次数下得到的A、P、R和F1度量见表3。

从表3可以看出,当训练集与测试集样本比例为7∶3时，进行到4次迭代随机森林分类时，模型A达到最大为78.21%，意味着在100个样本中大约有78个样本被正确归类；在3次迭代时P达到最大为70.27%，意味着在100个被预测为患病人群中大约有70人确实患病；在8次迭代时R达到最大为63.22%，表明100个患病人群中，约有63人能够被正确识别为患病；在第4次迭代时，综合考虑了P与R性能的F1度量达到最大为65.85%，综合考虑各个评价指标，可以认为在迭代随机森林进行到第4次迭代时，得到的分类模型最优。通过表3得到的实验结果可知，为了得到更好的A、P、R，不必一味增大迭代的次数，对于次数的设置一般3～6次即可。

表3 迭代随机森林不同迭代次数下A、P、R和F1度量 %

注：训练集与测试集样本比为7∶3。

迭代随机森林最明显的优势就是可以灵活地调整迭代次数，最优的A、P、R可能分别对应不同的迭代次数。例如表3中显示，最好的A在第4次时出现，而最好的R却在第8次时出现。因此迭代随机森林为我们提供了更多的选择余地，如果我们更关心A，可以选第4次迭代时的随机森林模型；如果更倾向于R，可以选定第8次迭代产生的随机森林模型。需要强调的是，在实际中相比于A，可能更关心R，即在患病人群中可以被正确识别为患病的比率，如果可以获得更高的R，那么在患病人群中就会有更多的糖尿病患者被正确诊断，进而得到及时治疗。

2.3 不同分类模型比较

为了对比不同分类模型的精度，分别采用随机森林(Random Forest， RF)、K最近邻(K-Nearest Neighbor， KNN)、基于不同核函数的支持向量机(Support Vector Machine， SVM)、人工神经网络(Artificial Neural Network， ANN)、Logistic回归(Logistic Regression， LR)和梯度提升机方法(Gradient Boosting Machine， GBM)、决策树(Decision Tree， DT)与迭代随机森林(Iterative Random Forests， IRF)进行比较，基于测试集得到的A、P、R、F1度量和运行时间见表4和表5。

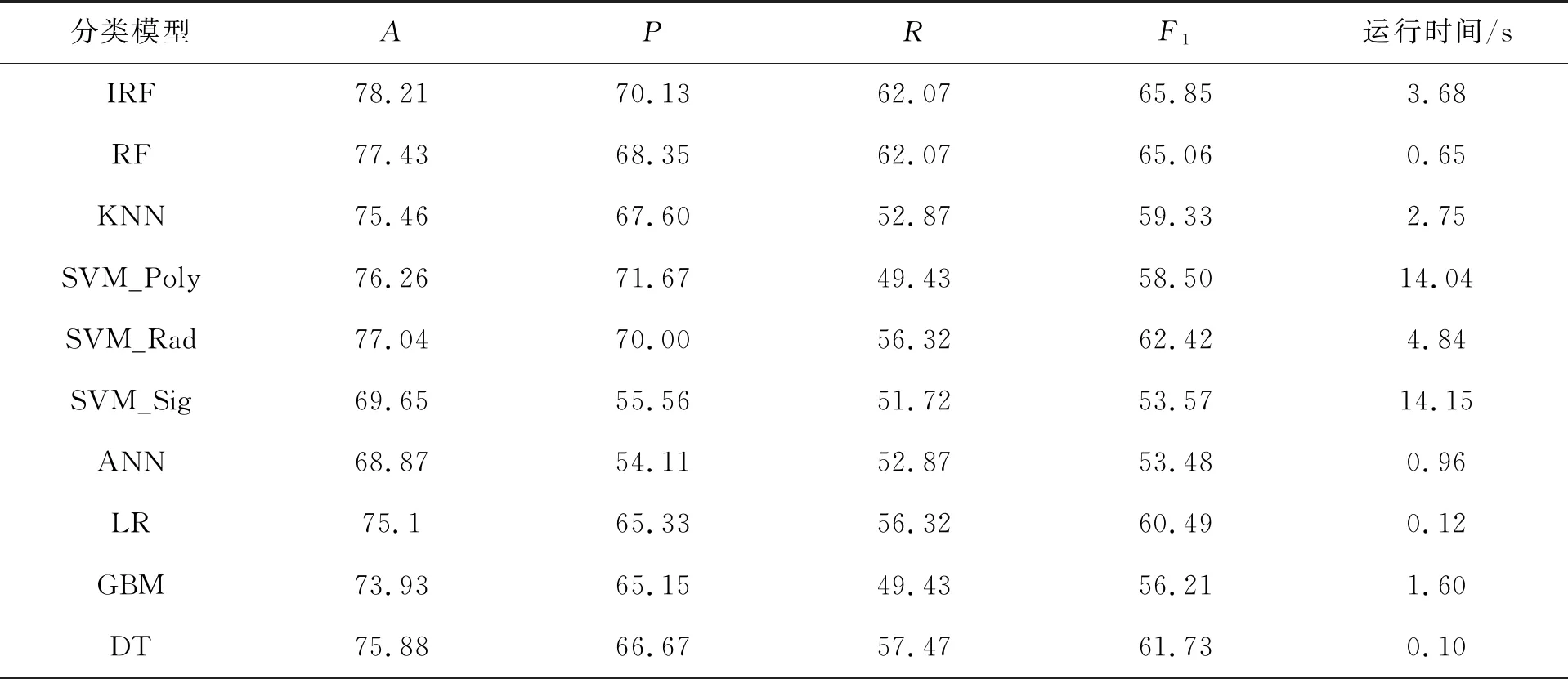
表4 不同分类模型A、P、R、F1度量和运行时间对比 %

注：训练集与测试集样本比为7∶3。

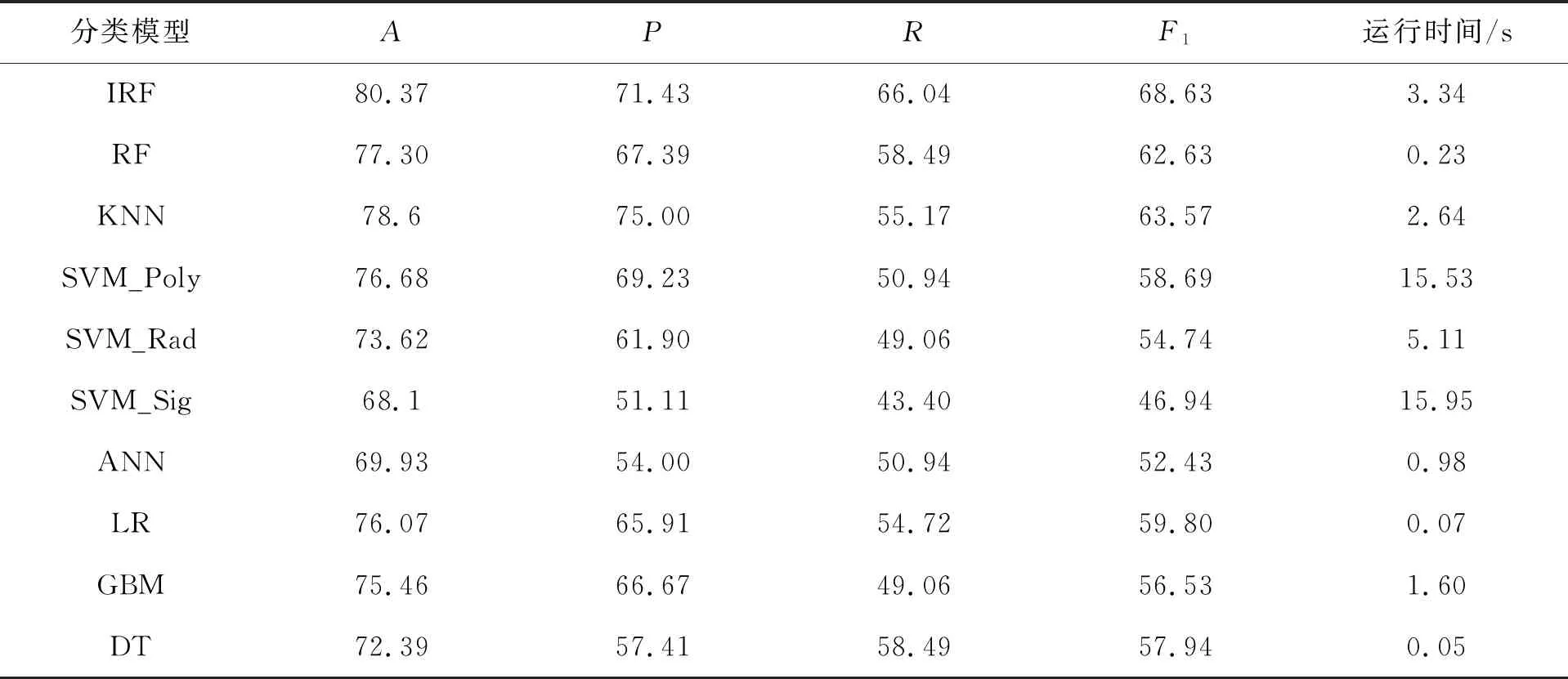
表5 不同分类A、P、R、F1度量和运行时间对比 %

注：训练集与测试集样本比为8∶2。

由表4和表5可以看出，对皮玛族成年女性是否患有糖尿病进行判别分类时，在8种分类模型中，迭代随机森林的A是最高的。当训练集与测试集样本比为7∶3时，A为78.21%、R为66.04%和F1度量的68.63%均为所有方法中最高的，而P在所有方法中排名第二，仅稍低于基于多项式核函数的支持向量机。当训练集与测试集样本比为8∶2时，迭代随机森林的A、P、R、F1度量均为所有分类方法中最高的，可见其分类优势明显优于其它分类模型。

从算法运行时间效率的角度进行比对，可以看出，基于8次迭代随机森林基于30%和20%的测试集用时分别为3.68 s和3.34 s，只少于支持向量机，但是应考虑到迭代随机森林要生成多个带有权重的森林，在算法默认的情形下，每个森林包含500颗决策树，同时该算法能保证提高分类预测的精度，可以认为迭代随机森林算法运行已经十分高效。

接下来绘制各个分类器下的ROC(Receiver Operating Characteristic)曲线[23]，并计算ROC曲线下的面积值AUC[24](Area Under ROC Curve)，进而更为直观地比较各个分类模型孰优孰劣，对应于文中的8个分类器的ROC曲线和AUC值如图3所示。

图3 基于30%的测试集迭代随机森林、随机森林、K最近邻、支持向量机、Logistic 回归、梯度提升机、决策树和人工神经网络分类模型的ROC曲线以及相应的AUC值

图3给出了各个分类算法的ROC曲线和AUC值，如果一个分类器的ROC曲线被另外一个分类器的ROC曲线完全包住，则可认为后者的性能要优于前者，按照这个原则可以看出，迭代随机森林、随机森林和K最近邻三个分类模型的ROC曲线显然包住了其它分类器的ROC曲线，说明这三个分类器的分类效果要优于其它分类模型。由于迭代随机森林、随机森林和K最近邻的ROC曲线之间存在交叉，此时就要借助于AUC的值,即计算ROC曲线下方的面积比较分类器之间的性能，图3的最右侧给出了各个分类模型对应的AUC值，迭代随机森林的AUC值为0.742 7,高于K最近邻的0.740 7和随机森林的0.736 8。

通过实验对比，无论是基于A、P、R、F1度量,还是借助于ROC曲线和AUC值，可以得出迭代随机森林对于皮玛族印第安女性糖尿病数据集的分类性能，是众多的分类算法中最优的。正是由于“迭代随机森林算法”可以较好检验出特征间的高阶交互作用，因此,在提高数据集的预测精度上表现的更为出色。

3 结 语

提出一种可检测变量特征间交互作用的迭代随机森林算法，应用于皮玛族成年女性Ⅱ型糖尿病数据集分类研究。借助于迭代随机森林算法，基于精度与基尼系数的平均减少量给出了影响糖尿病病情属性特征的重要性排序，发现血糖浓度、身体质量指数和年龄是影响糖尿病病情的三项最重要指标。

为了横向比较迭代随机森林与目前主流的机器学习方法的分类效果，分别选取随机森林、K最近邻、支持向量机、人工神经网络、Logistic回归、梯度提升机和决策树方法对皮玛族糖尿病数据集进行分类。实验分析表明，基于30%和20%的测试集迭代随机森林的精度分别达到78.21%和80.37%，优于其它的7种分类模型；同时又借助于ROC曲线和AUC值，在基于30%的测试集上，迭代随机森林的ROC曲线也在其它分类模型ROC曲线的上方且AUC值也是所有分类方法中最高的。

通过迭代随机森林算法可以对糖尿病进行有效地监测与识别，并挖掘出患病因素，及时地对糖尿病作出提早预防和风险控制，进而降低医疗成本,减少误诊率。