小井眼开窗侧钻用高抗弯钻具接头性能分析与结构参数优化
2020-01-03况雨春陈永龙闵桃源
况雨春 陈永龙 闵桃源
西南石油大学机电工程学院,成都,610500
0 引言
近年来,随着油田的不断开发以及生产作业井年限的不断增长,我国大多数油田已进入中后期开发阶段。一方面,由于部分老井出现工程事故、套管损坏等原因导致无法采用常规修井技术使破损井得到恢复;另一方面,在对井网进行调整时,为了降低综合开发成本,利用小井眼开窗侧钻技术,在原有井筒基础上进行二次开发,极大地减少了资金投入[1]。但小井眼开窗侧钻中容易出现“两小一高”(即排量小、扭矩小、压耗高)的问题,使得钻进动力不足,循环压耗高,作业成本高,钻井效率低。考虑到φ139.7 mm套管连续钻井技术在国内技术配套尚不成熟,且无法进行旋转钻进来降低有效侧钻深度[2],故采用φ80 mm直连型钻杆,以有效提高钻井效率,提升钻井液携岩能力,有效传递工作扭矩,提升油气开采效率。
随着小井眼开窗侧钻技术的广泛应用,由井下弯曲段引起的钻具接头失效问题日益突出。据不完全统计,国外64%的油套管失效事故发生在螺纹处,国内则高达86%[3-4],造成了极大的经济损失。究其原因,主要是钻具接头在承受紧扣扭矩的同时还要承受弯曲段弯曲载荷作用,弯曲段斜率不同,接头螺纹承受的弯曲应力也不同,因此,分析弯曲载荷作用下接头力学性能就显得尤为重要。近年来,国内外学者对油套管接头进行了大量试验和理论研究,得到了较为准确的结果。BAHAI[5]利用二维轴对称模型分析轴向力和弯曲载荷作用下钻具接头应力集中因子;兰洪波等[6]设计了新型双台肩钻具接头,分析了螺纹在不同工况下的应力;陈守俊等[7]采用二维圆锥管螺纹模型,分析不同过盈量下套管螺纹的应力变化情况;SHAHANI等[8]通过三维和二维有限元模型对比,研究不同载荷作用下钻杆接头的接触应力分布; FUKUOKA等[9]对带有螺旋升角的接头螺纹三维模型进行了有限元分析;祝效华等[10]建立了套管接头三维有限元模型,分析拉弯复合载荷下的力学行为。然而,由于二维轴对称模型不带螺旋升角,故无法模拟螺纹上扣且无法准确表征偏执载荷作用下的应力变化情况,虽然部分文献分析了钻具接头三维有限元模型,考虑了螺旋升角作用,但是下井前未对接头施加紧扣扭矩,因此,同样无法准确得到接头的力学性能以及疲劳寿命。
针对上述问题,本文建立了高抗弯钻具接头螺纹的三维有限元模型,采用实际工况的加载顺序,并基于正交优化试验方法,对影响螺纹受力的关键因素进行正交优化,获得高抗弯钻具接头关键参数,对比计算优化前后接头的力学性能,突出其在小井眼开窗侧钻中的优势。
1 弯曲载荷作用下钻具接头受力分析
小井眼开窗侧钻中,钻具接头承受弯矩载荷作用时,弯矩载荷由台肩和螺纹牙共同承担,且台肩处产生的应力对螺纹牙具有一定的增强作用(图1)。设钻具接头承受的弯矩为M,台肩处承受的弯矩为M1,螺纹牙根部承受的弯矩为M2,则M=M1+M2。考虑到M1和M2的相对大小与台肩及螺纹牙根部的抗弯刚度有关[11],有
(1)
其中,J1为台肩截面惯性矩,J2为公螺纹牙根部截面惯性矩,E为接头材料弹性模量,则有
M=M1+M2=M2(1+J1/J2)=M1(1+J1/J2)
(2)
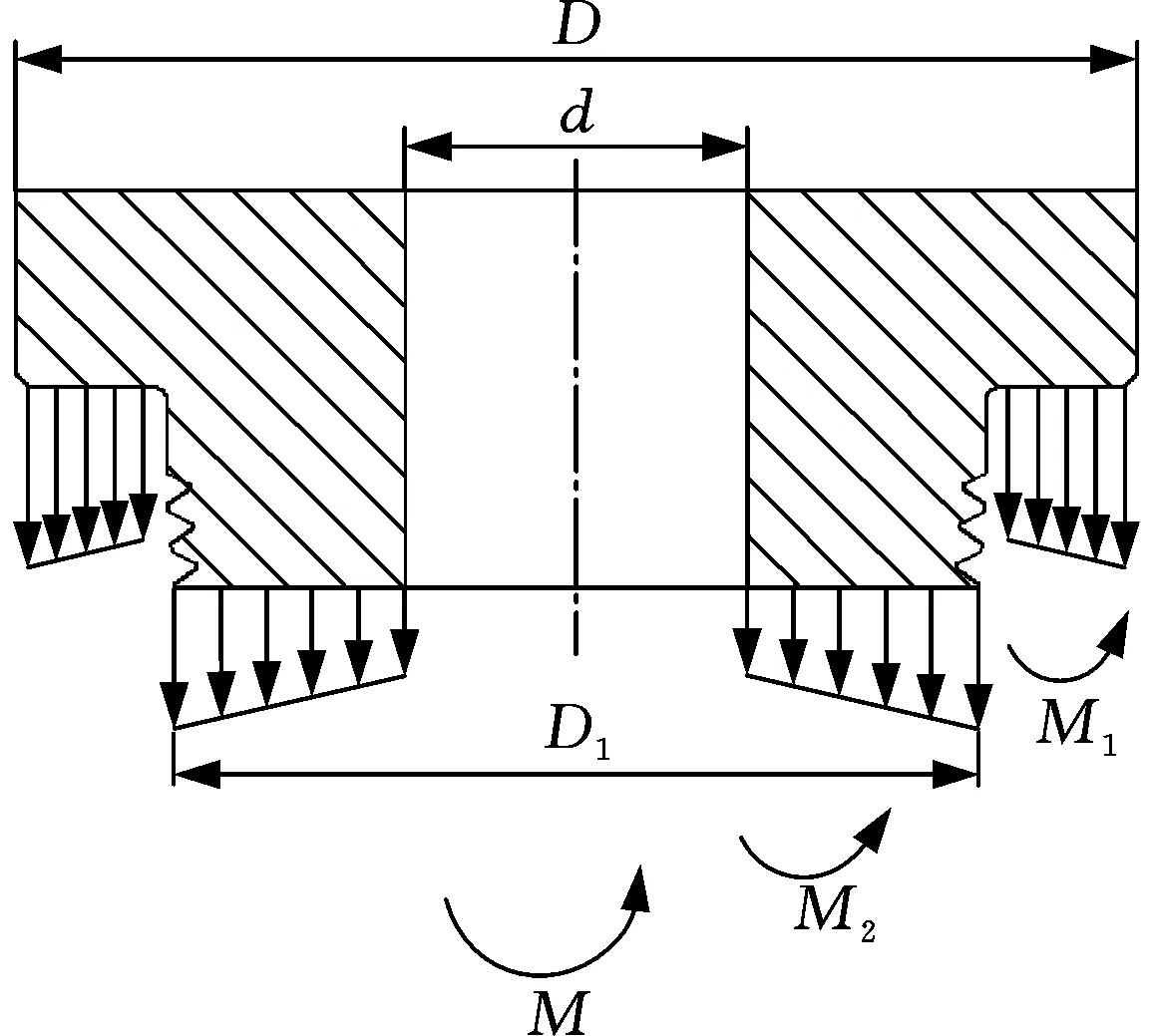
图1 钻具接头外螺纹弯曲应力分布示意图Fig.1 Bending stress distribution chart of the tool joint
在钻井过程中,钻杆接头往往处于复杂的交变载荷作用下,为保证接头台肩面在工作时不分离,由弯曲载荷在台肩面引起的最大应力σmax不应大于预压力σ1,假设
σmax=ασ1
(3)
σmax=M1/W1
(4)
M1=2J1ασ1/D
(5)
式中,W1为抗弯截面模量。
其中,常数α(α≤1)表征钻杆受弯曲载荷的程度;D为钻具接头外径。由式(4)可求得台肩处所能承受的弯矩。由式(1)和式(5)可求得公螺纹所承受的弯矩为
(6)
钻具接头在承受弯曲载荷时,公螺纹承受的最大弯曲应力在第一圈螺纹牙根处,其弯曲应力
σpin=D1ασ1/D
(7)
式中,D1为螺纹齿顶圆直径。
母扣螺纹牙根处因弯曲产生的最大应力
(8)
式中,Jβ为母螺纹牙根部β截面上的最大弯曲应力;d为接头内径。
由上述分析结果可知,若减小因弯曲载荷在螺纹牙根部产生的应力即减小弯矩M2,可通过设计双台肩钻具接头和改变螺纹参量的方式,利用主副台肩共同承担弯曲载荷,增强螺纹牙抗弯能力,以达到减小峰值弯曲应力、提高钻具接头抗弯性能的目的。
基于钻杆用双台肩矮牙特锥扣模型(图2),利用有限元软件对钻具接头受力特点进行分析,并采用正交优化方法对螺纹锥度、牙型角、螺距等关键参数进行优化,在不减小钻具接头抗拉/压、抗扭能力的前提下,提高接头抗弯能力,对其进行结构改进,旨在设计出能满足小井眼开窗侧钻的钻具接头。
2 钻具接头弹塑性有限元模型
2.1 钻具接头本构模型试验
钻具接头所用材料为SAE4137H合金钢,系各向同性弹塑性材料。使用对接头材料(3个相同的试样,即试样①~试样③)进行拉伸试验,获得了应力应变曲线,从中可以得出:材料弹性模量为210 GPa, 屈服强度为860 MPa,抗拉强度为975 MPa,泊松比为0.29。考虑到含40%~60%质量锌粉末的螺纹脂的影响,配合面间(包括
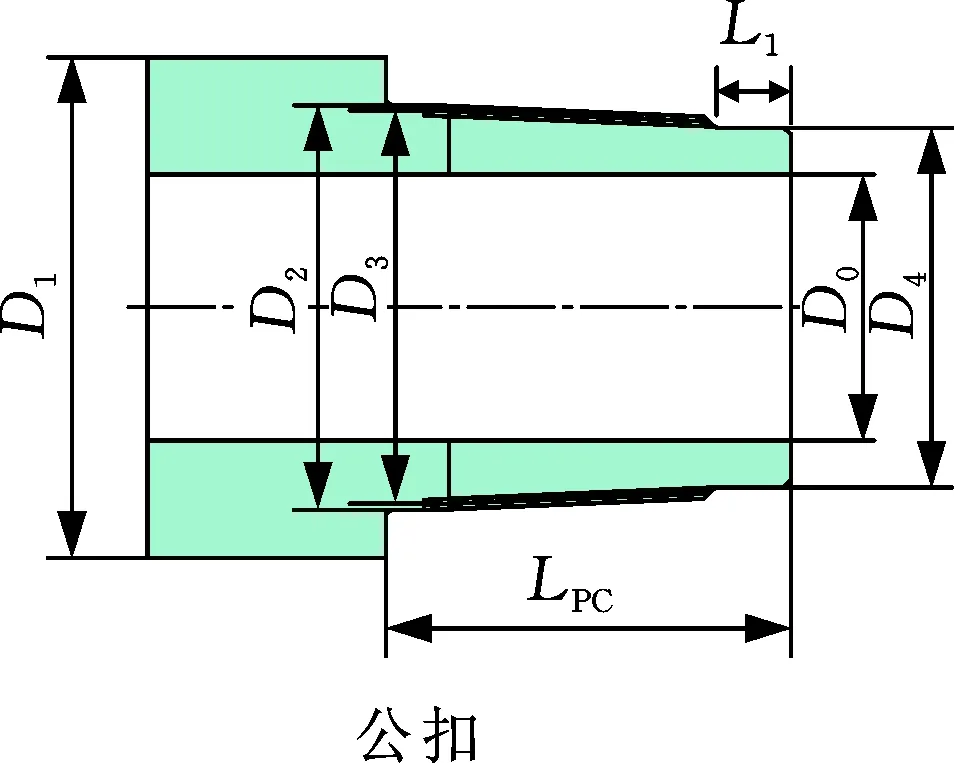
(a) 公螺纹

(b) 母螺纹
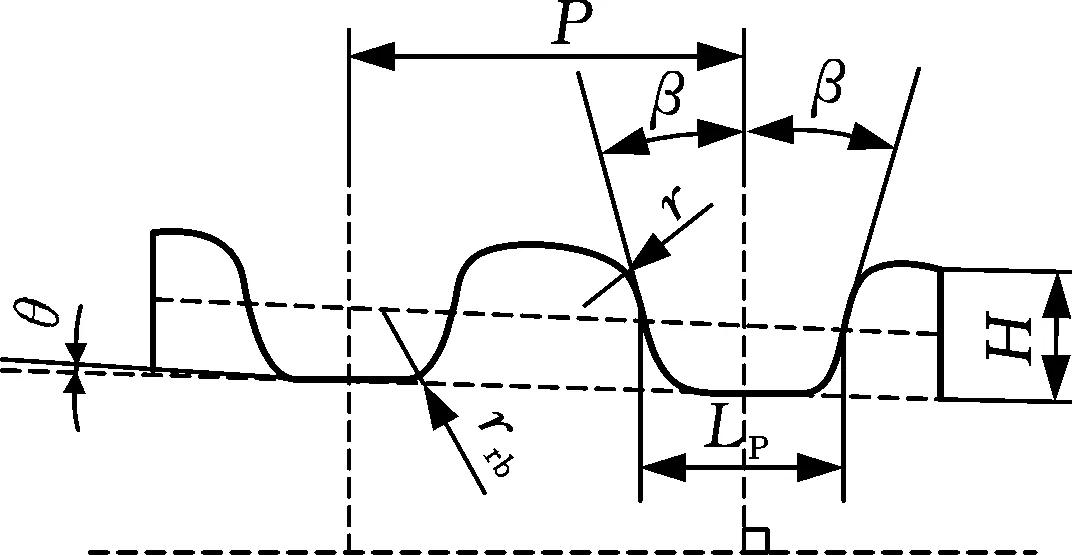
(c) 螺纹牙型
螺纹之间和台肩面之间)的摩擦因数取0.08[12]。
螺纹接头在受到复杂载荷作用,当某一位置应力达到材料的屈服极限时,该位置就会发生一定的弹塑性变形。在螺纹接头有限元分析时,为了真实反映出螺纹受力,有必要定义其在弹塑性阶段的应力应变,在workbench中采用真实应力应变关系来定义塑性阶段的变化,它与名义应力和应变的关系为[13]
ε=ln (1+εnom)
(9)
σ=σnom(1+εnom)
(10)
其中,εnom为名义应变,σnom为名义应力。材料的真实应力-应变关系如图3所示。
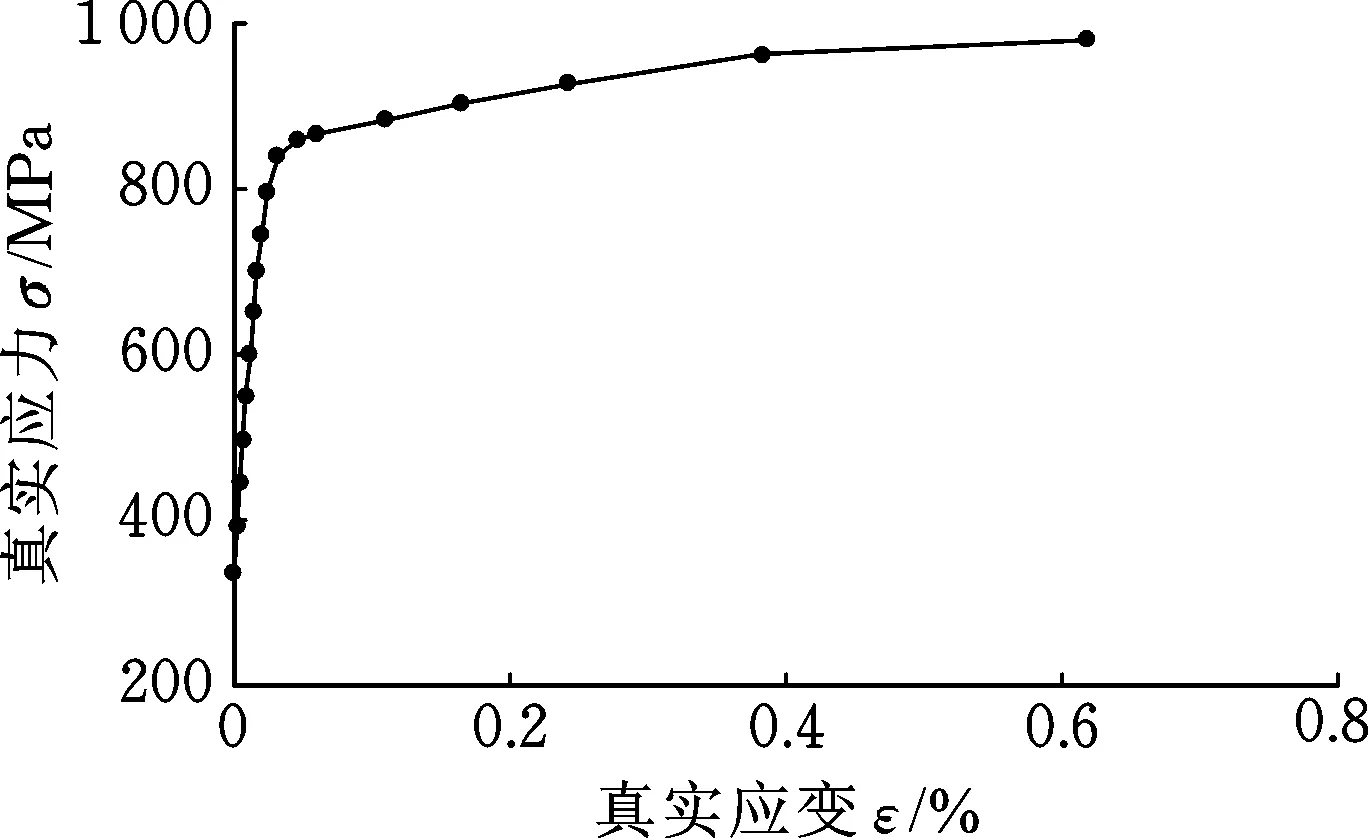
图3 真实应力应变曲线Fig.3 True stress-strain curve
2.2 钻具接头模型的网格划分
本文以矮牙特锥扣钻具接头为研究对象,为了构建高计算精度和高效率的有限元模型,在台肩和螺纹牙接触部分划分精细网格,在远端(即未接触部分)采用相对稀疏的网格。采用Solid185六面体单元对模型进行网格划分,网格数量为879 260,节点数为951 179。
2.3 有限元仿真模型试验验证
为了确保数值仿真结果的可靠性,本文通过钻具接头胀扣试验,利用拆装架液压装置对螺纹接头施加紧扣扭矩(图4a),对比研究不同紧扣扭矩下接头外缘的膨胀变化规律。试验以API标准NC31型特殊扣为研究对象,建立与图4b中相同规格的连接螺纹力学模型。为了保证试验结果的可靠性,改变接头螺纹锥度和外径,分别测得3组不同结构接头胀扣数据,如图5中结构①~结构③。利用有限元仿真结果与试验数据进行对比(图5)。试验结果与有限元仿真结果变化趋势相同,峰值差异不超过30%,可以忽略不计。总体上两者结果吻合性较好,验证了三维模型建模的准确性以及仿真结果的可靠性,表明所建模型及分析方法能满足钻具接头力学性能研究的需要。

(a) 试验台架

(b) 螺纹接头
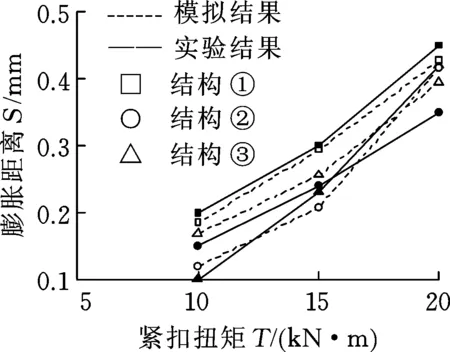
图5 试验结果与有限元结果对比Fig.5 Comparison of experimental results and finite element results
3 弯曲载荷对钻具接头连接强度和密封性能的影响
接头螺纹在下井前须承受一定的上扣扭矩,对于需要开窗侧钻的老井和破损井,扭矩载荷和弯曲载荷是其在井下承受的主要载荷。由于螺纹在上扣之后将持续影响其在后续工况中的受力,弯曲载荷作用下接头台肩和螺纹牙啮合面接触状态以及受力状况将变得极其复杂,故这种受力变形将决定接头的连接强度和密封性能。为更有效地模拟钻具接头在井下受力情况,对钻具接头进行三维有限元分析,为避免数值振荡,采用光滑的加载曲线进行加载(图6)[14]。第一步施加紧扣扭矩,加载完毕后卸载;第二步施加弯曲载荷,加载完毕后保持作用不卸载[15]。
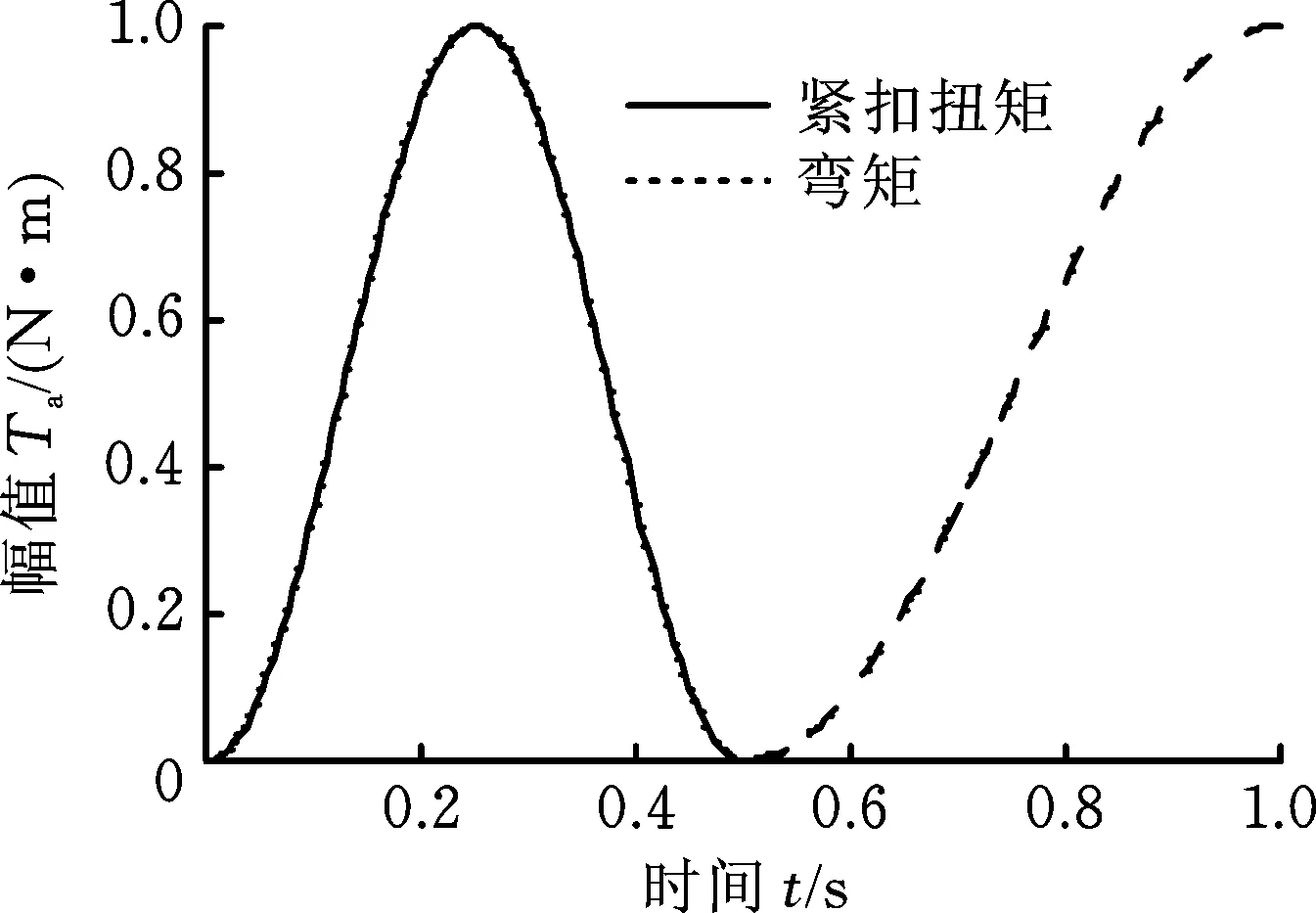
图6 加载曲线Fig.6 Loading curve
3.1 弯曲载荷对钻具接头连接强度的影响
在小井眼开窗侧钻中,弯曲载荷作用对钻具接头连接强度的影响是不容忽视的。对比钻具接头仅承受紧扣扭矩、承受紧扣扭矩并施加不同弯曲载荷和轴向载荷时连接螺纹最大等效应力的变化情况,如图7所示。可以看出,钻具接头仅承受紧扣扭矩时,螺纹牙部分最大等效应力为597 MPa;当施加100 kN弯曲载荷时,螺纹部分最大等效应力增大了125 MPa;在材料弹性阶段,应力呈线性增加趋势,当弯曲载荷超过200 kN时,应力变化趋势减缓,在300 kN时达到材料的拉伸极限,总体变化规律满足材料的弹塑性本构关系。施加轴向载荷时,螺纹部分最大等效应力增速明显减小,最大等效应力增大35 MPa,仅为施加弯曲载荷时的10%,表明钻具接头对弯曲载荷更加敏感,它对连接螺纹应力状态影响很大,因此,在小井眼开窗侧钻中须考虑弯曲载荷的影响。
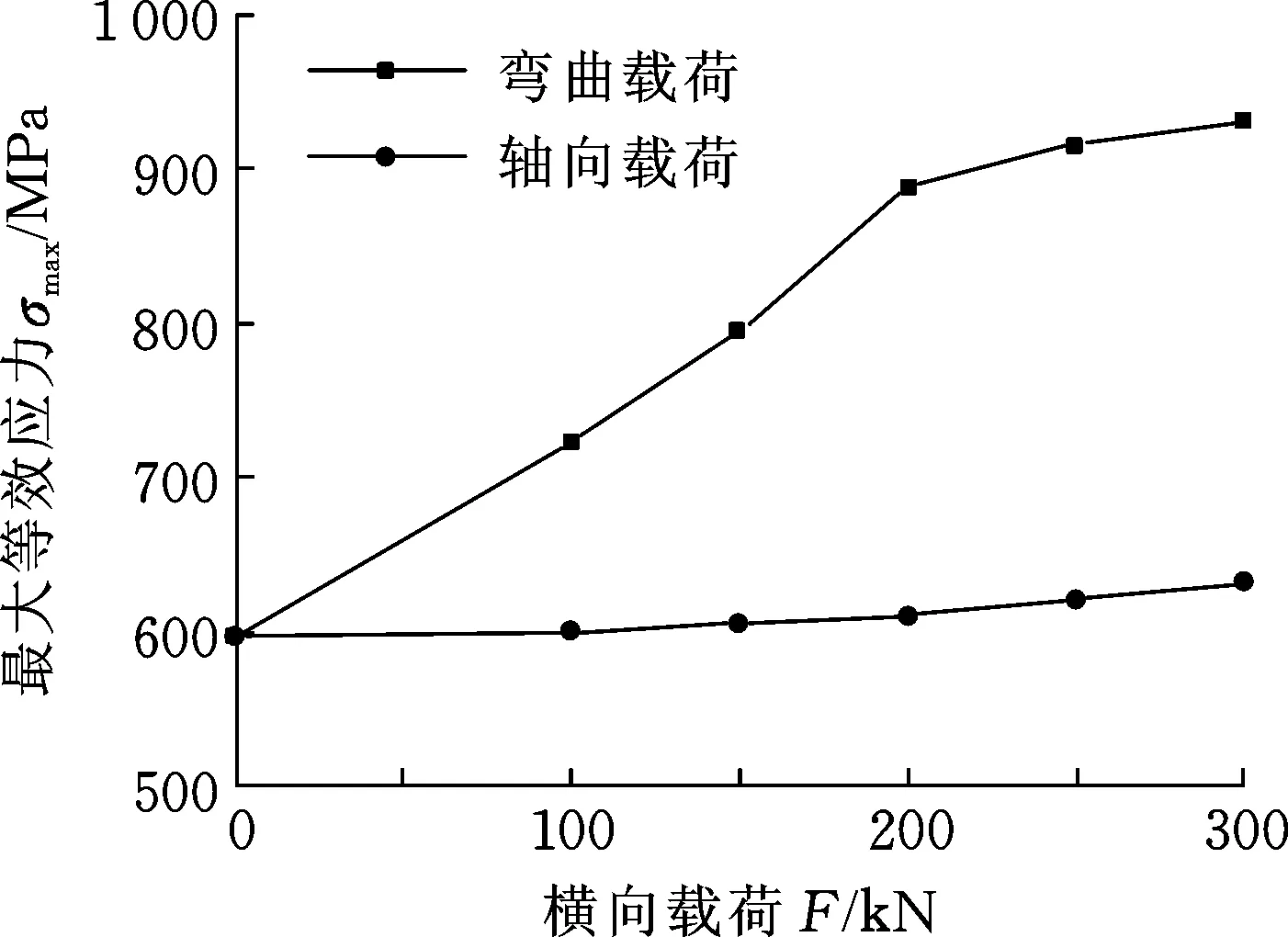
图7 弯曲载荷作用下连接螺纹最大等效应力Fig.7 Maximum equivalent stress of the threaded connection under bending load
不同横向载荷作用时各螺纹牙最大等效应力变化情况如图8所示(规定靠近主台肩第一圈螺纹牙为第1牙,依次向右类推)。等效应力是评价钻具接头各螺纹牙连接强度的关键指标,可以看出,随着弯曲载荷逐渐增大,各螺纹牙应力呈现出逐渐增大的趋势,最大应力集中在第一圈及最后一圈牙根处,而中间段螺纹牙应力变化平缓,总体上呈现出“中间低,两边高”的特点。当弯曲载荷为250 kN时,靠近主副台肩处的螺纹牙根部应力已经达到材料的屈服极限,继续增大外载荷容易导致钻具接头出现疲劳破坏,螺纹牙根部产生裂纹。
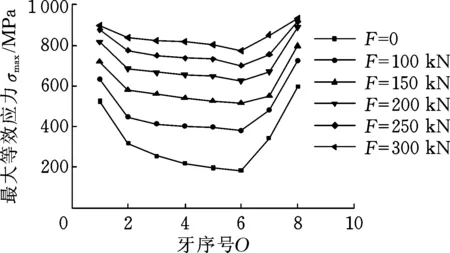
图8 不同横向载荷作用下螺纹牙最大等效应力Fig.8 Maximum equivalent stress of thread teeth under different transverse loads
不同弯曲载荷下第一圈及最后一圈螺纹牙周向应力变化情况如图9、图10所示。可以看出,在弯曲载荷作用下螺纹牙应力逐渐增大的同时,沿周向分布不均匀性也在增大。当仅承受紧扣扭矩时,螺纹牙沿周向应力分布较均匀;当施加弯曲载荷时,公扣第一圈螺纹牙应力主要集中在拉伸端附近。施加300 kN弯曲载荷时,公扣第一圈螺纹牙拉伸端附近应力达到了材料的屈服极限,但在压缩端附近应力值较小,导致产生周向应力分布不均匀现象。公扣最后一圈螺纹牙周向应力较第一圈螺纹牙相比相差较大,其最大应力主要集中在压缩端和拉伸端之间,其余部位为低应力值区域,最后一圈螺纹牙同样在300 kN时发生屈服。根据钻具接头在弯曲载荷作用下的受力状态,弯曲载荷对连接螺纹性能影响很大,进行小井眼开窗侧钻时,应充分考虑井眼曲率对接头连接强度的影响,进而减小因外载荷过大而导致钻具接头挤毁的概率。
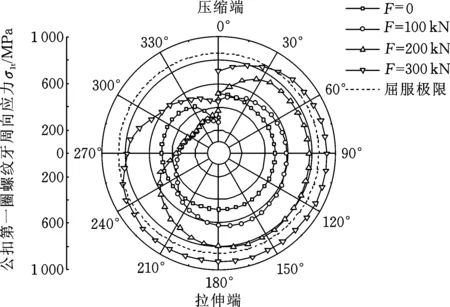
图9 公扣第一圈螺纹牙应力Fig.9 Stress on the first circle of pin thread tooth

图10 公扣最后一圈螺纹牙应力Fig.10 Stress on the last circle of pin thread tooth
3.2 弯曲载荷对钻具接头密封性能的影响
为了研究小井眼开窗侧钻中弯曲载荷对钻具接头密封性能的影响,分析了其在弯曲载荷作用下主副台肩面以及螺纹牙啮合面上接触压力沿周向变化的情况。钻具接头在不同弯曲载荷作用时第一圈及最后一圈螺纹牙接触压力如图11、图12所示。在未承受弯曲载荷时,螺纹牙啮合面沿周向接触压力分布较均匀。虽然弯曲载荷作用时螺纹牙一端受压一端受拉,但此时第一圈及最后一圈螺纹牙接触压力并未受到剧烈影响,且接触压力变化幅度较小,表明螺纹牙啮合面密封良好。在300 kN横向载荷作用下,第一圈及最后一圈螺纹牙接触压力保持在450 MPa以上,虽然起到了较好的密封效果,但最大接触压力值达到了750 MPa,考虑到井下工况复杂,动载荷持续作用下易导致啮合面因压力过高而产生粘扣,破坏其密封性能。
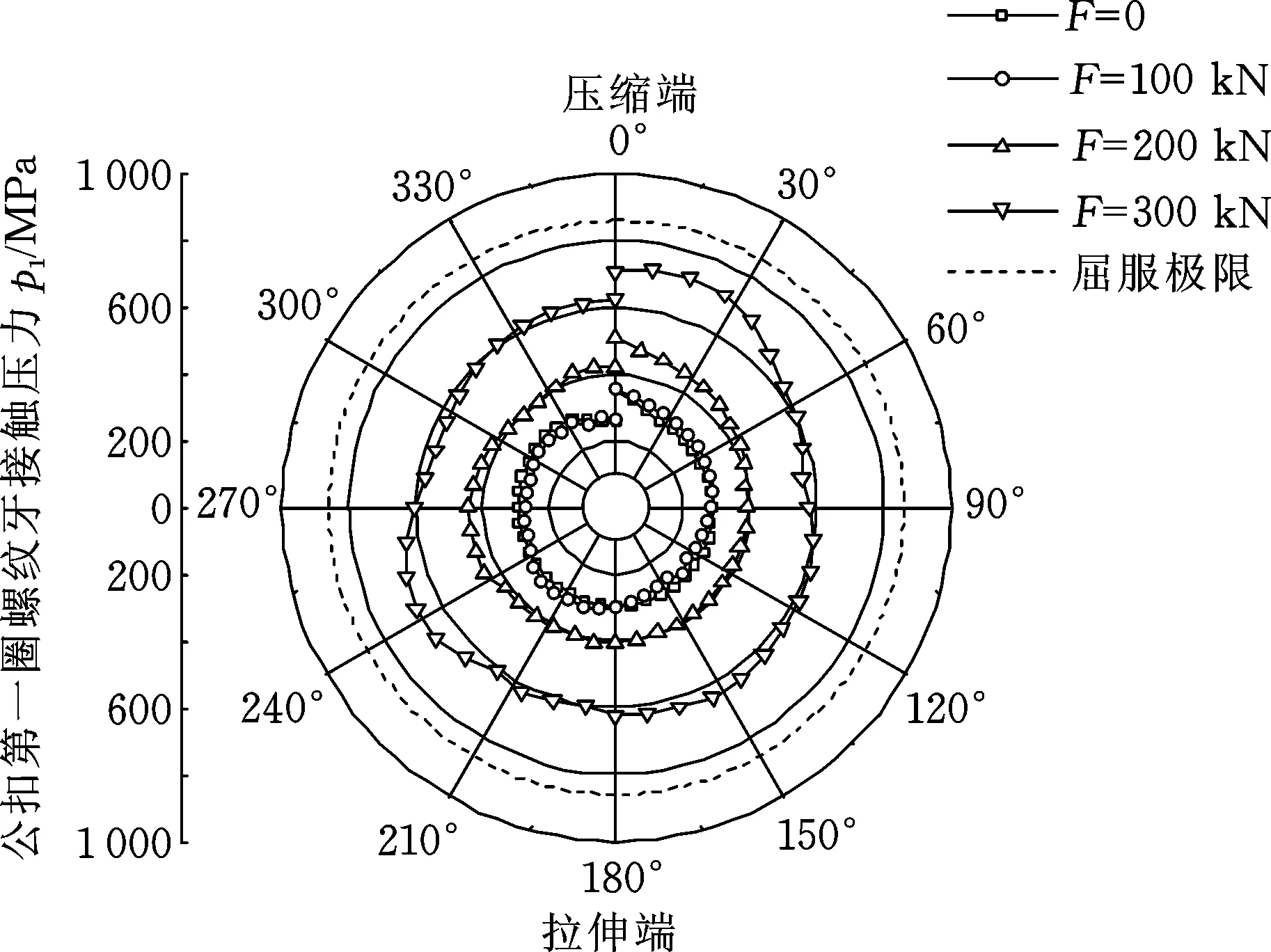
图11 公扣第一圈螺纹牙接触压力Fig.11 Contact pressure on the first circle of pin thread tooth

图12 公扣最后一圈螺纹牙接触压力Fig.12 Contact pressure on the last circle of pin thread tooth
钻具接头主、副台肩面周向接触压力如图13、图14所示。可以看出,主副台肩啮合面接触压力主要集中在压缩段,导致受压段接触压力过大。当横向载荷为200 kN时,副台肩部分啮合面已经达到材料的屈服极限,且增长速度高于主台肩处接触压力。由于接触压力往压缩端偏移,导致周向压力分布极不均匀,拉伸端在100 kN载荷下出现部分啮合面脱离现象。由此可见,弯曲载荷越大,主副台肩啮合面密封失效面积越大,对钻具接头密封性能影响越严重,且过大的接触压力容易致使啮合面受压一侧产生黏接以及过度磨损,受拉一侧(即低接触压力区域)出现密封失效,钻井液通过台肩或螺纹牙进入钻具接头内部而出现应力腐蚀,因此,弯曲载荷不仅对钻具接头连接强度影响很大,对其密封性能的影响也不容忽视。
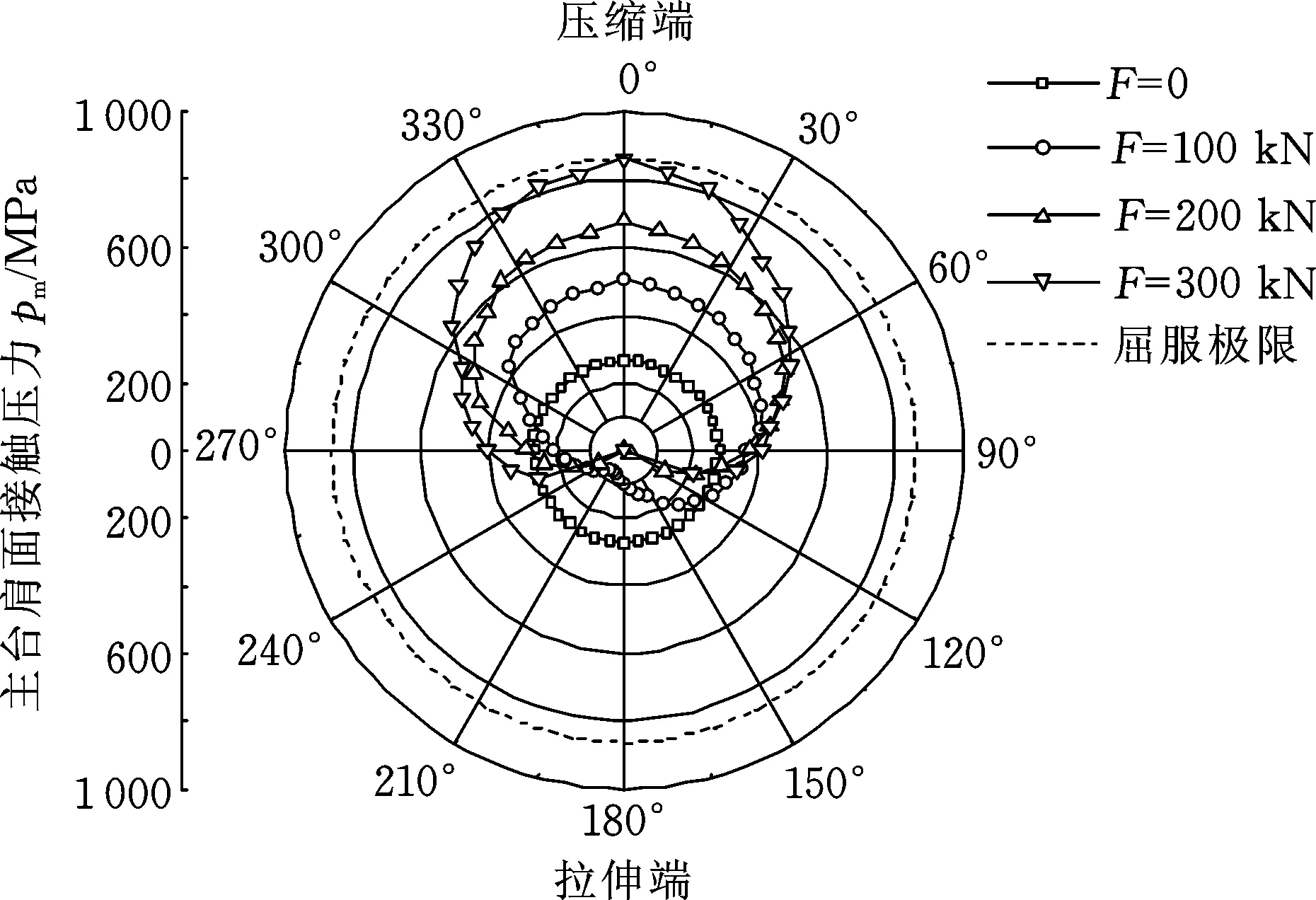
图13 主台肩面接触压力Fig.13 Contact pressure of the main shoulder surface
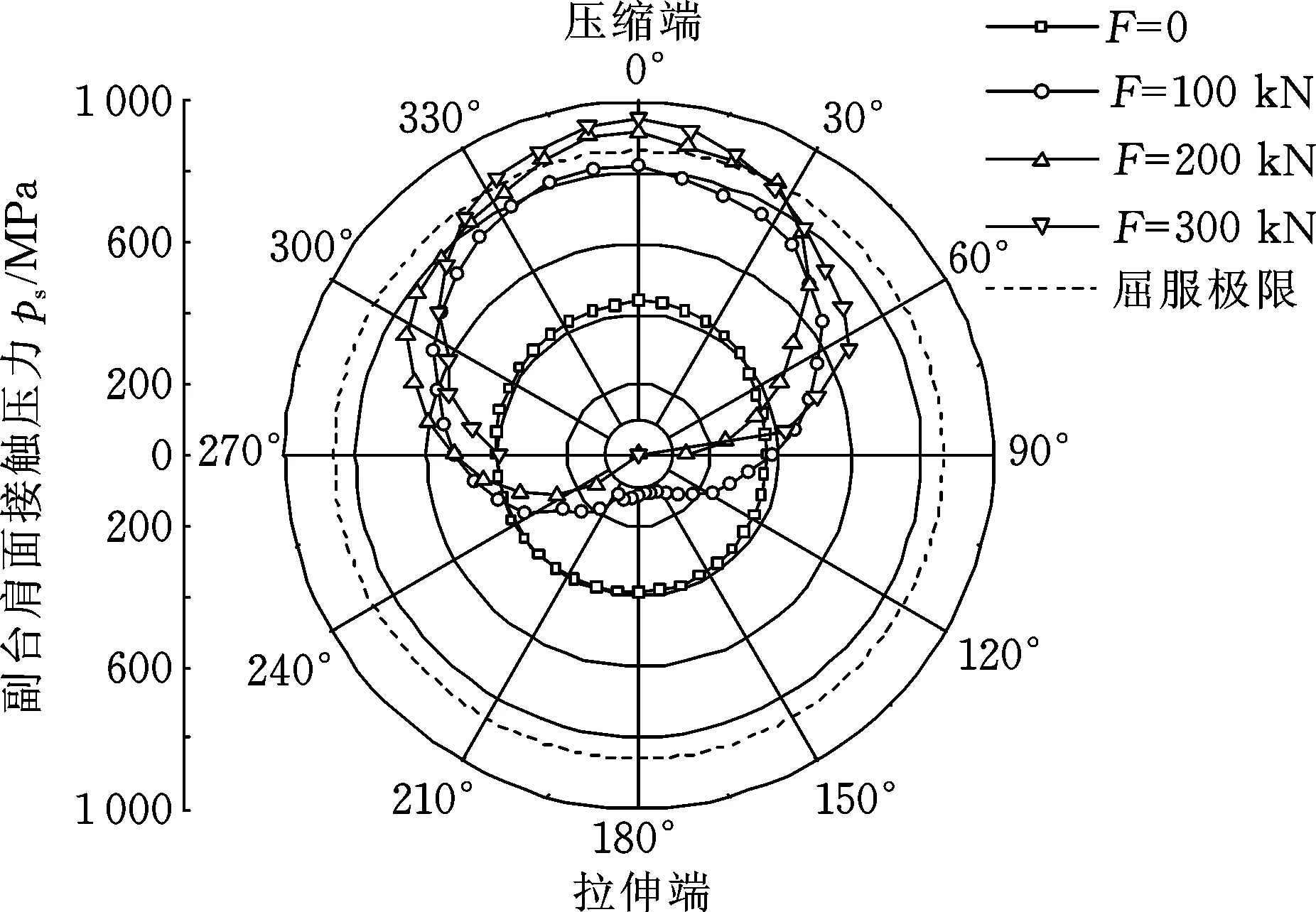
图14 副台肩面接触压力Fig.14 Contact pressure of the side shoulder surface
4 高抗弯钻具接头主要结构参数正交优化
本文基于双台肩特殊扣型钻具接头,考虑螺纹结构参数间相互耦合作用,引入正交优化试验方法,设计出承载性能较优的高抗弯钻具接头。通过此前建立的双台肩钻具接头,对影响螺纹承载性能的关键结构参数(锥度、螺距及牙型角等)进行正交优化,利用正交表“均衡搭配”和“整齐可比”的基本原则,设定4个结构参数为试验因素,每个因素包含5种水平,在一定范围内使各水平均匀取值,总共进行25次正交试验,使得计算结果和取值更加合理和具有代表性。
以钻具接头抗弯性能为分析指标,在不减小接头抗扭性能和抗拉/压性能的前提下进行正交优化,基于表1中设定的试验因素和试验水平,设计了4因素5水平的正交表,在横向弯曲载荷作用下,对不同参数组合下螺纹接头应力结果进行了极差分析,极差大小即体现试验因素对接头抗弯性能的影响程度,试验结果分析表见表2。可以看出,各试验因素对抗弯性能影响的主次顺序分别为螺距、导向侧角度、承载侧角度及锥度。在试验水平范围内,其最优组合为:锥度1∶10,螺距7牙/英寸,承载侧角度20°,导向侧角度14°。
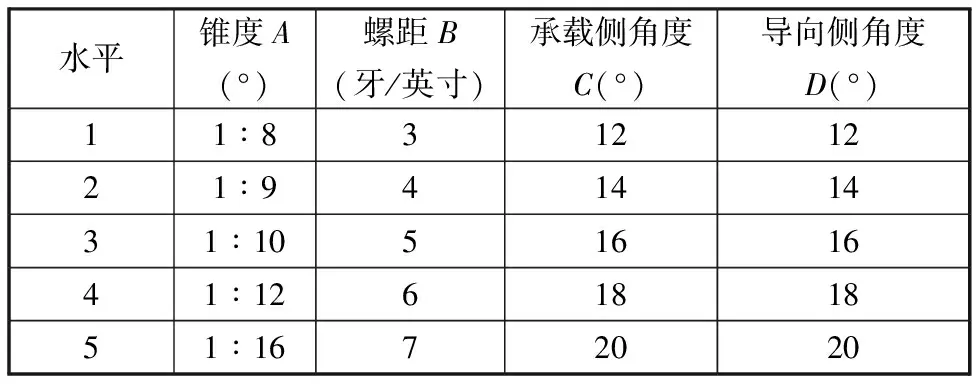
表1 钻具接头试验因素水平表
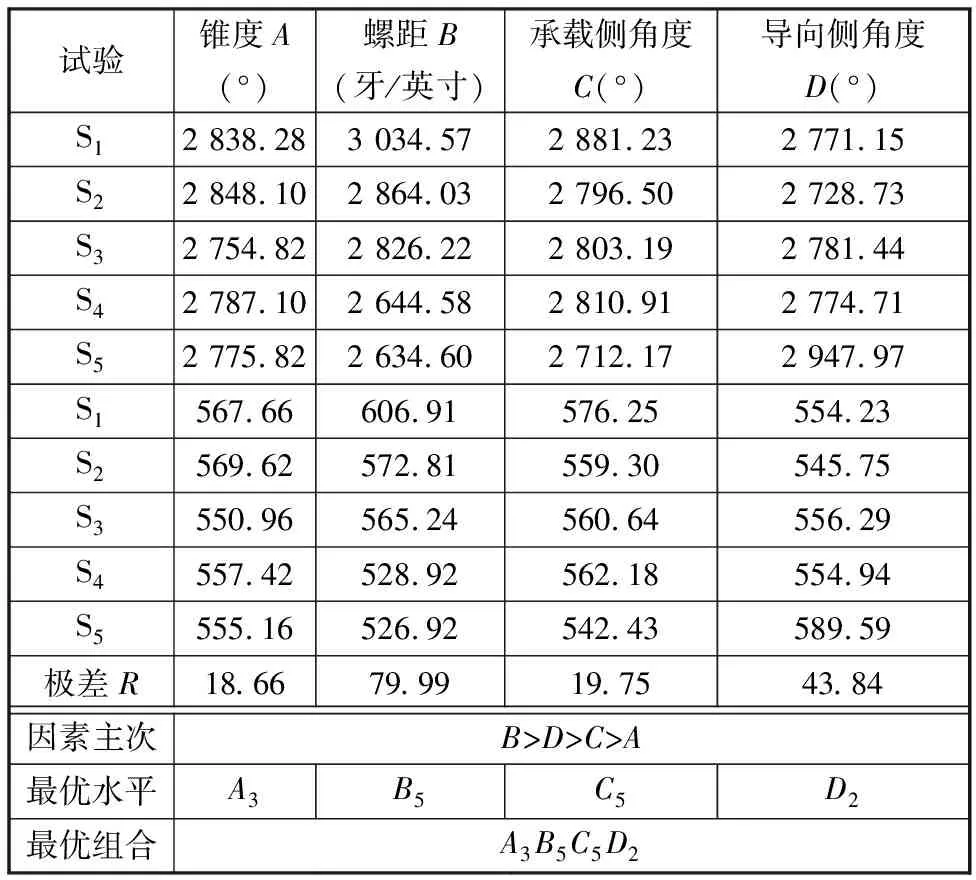
表2 正交优化试验结果分析表
4.1 钻具接头抗拉/压性能对比分析
对比计算高抗弯钻具接头与API钻具接头在不同轴向拉/压力作用下的最大等效应力。API结构与ST高抗弯结构性能对比如图15所示,可以看出,在相同轴向拉力作用下,高抗弯钻具接头最大等效应力小于API接头最大等效应力,且母扣螺纹牙应力明显小于公扣螺纹牙应力。两种钻具接头在不同轴向拉力作用时最大应力满足材料弹塑性变化规律,在1 MN时达到材料的屈服极限。API钻具接头公扣和母扣最大等效应力大于高抗弯钻具接头应力,表明在抗拉性能方面,ST抗弯接头优于API接头。
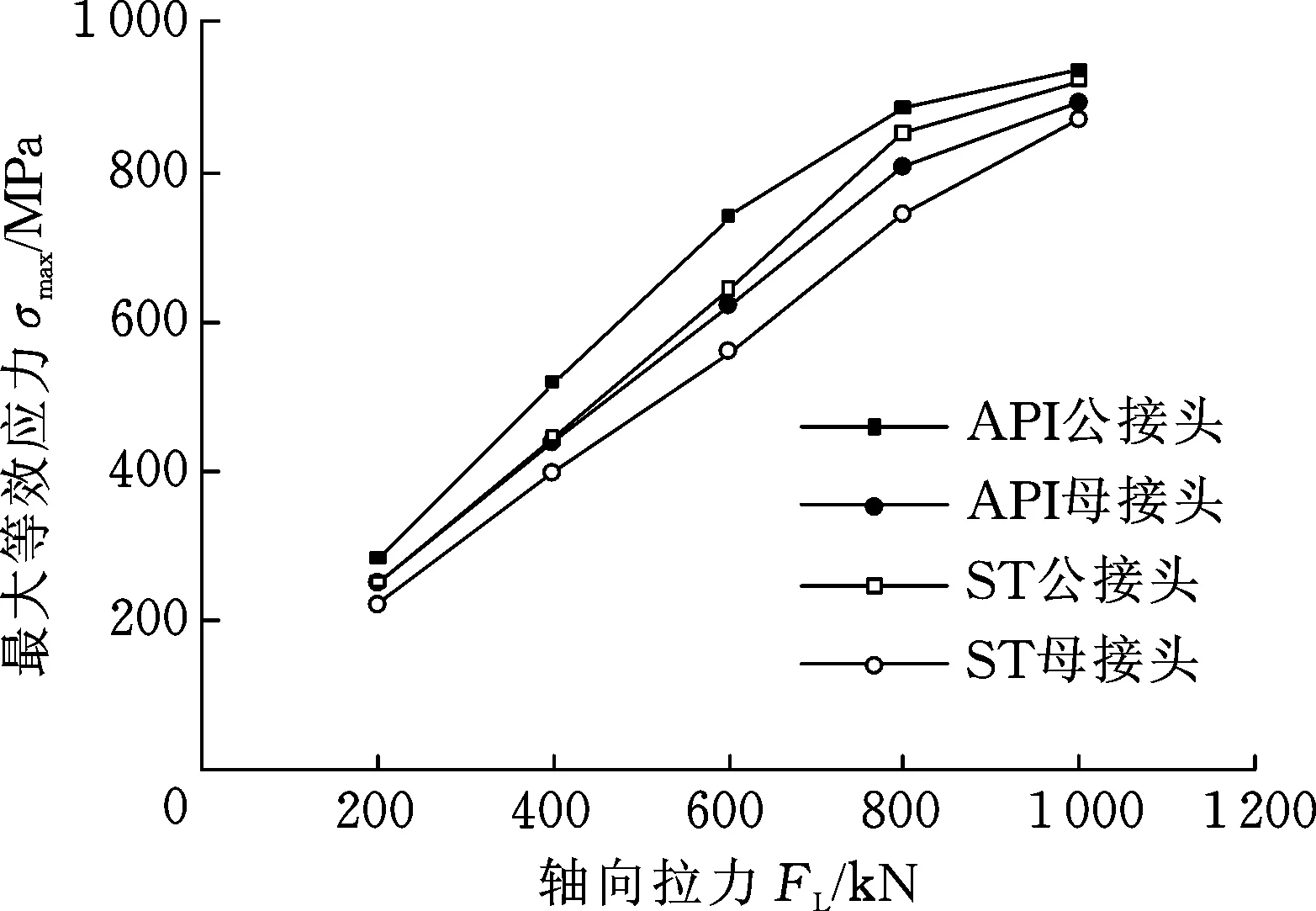
图15 API结构与ST结构抗拉性能对比Fig.15 Comparison of tensile properties between API structure and ST structure
不同压力下API结构与ST高抗弯结构性能对比如图16所示,可以看出,两种钻具接头变化趋势基本相同,在2 MN压缩载荷作用时应力呈线性关系变化,当外力超过2.5 MN时最大等效应力增速减缓,且达到材料的屈服极限。总体上API钻具接头公扣和母扣最大等效应力大于ST高抗弯接头最大等效应力,表明ST接头在抗压性能方面优于API接头。
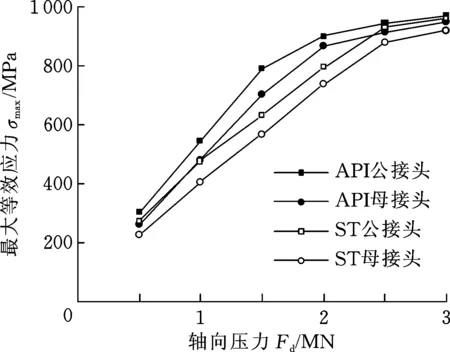
图16 API结构与ST结构抗压性能对比Fig.16 Comparison of compressive properties between API structure and ST structure
4.2 紧扣扭矩对比
对比计算高抗弯钻具接头与API钻具接头在紧扣扭矩作用下的最大等效应力,结果如图17所示。可以看出,两种钻具接头最大等效应力变化趋势大致相同,在紧扣扭矩作用下,API结构钻具接头最大等效应力大于ST结构钻具接头等效应力,且公扣上产生的应力均大于其对应母扣的最大应力。随着紧扣扭矩逐渐增大,两种扣型钻具接头应力变化规律趋近于材料的弹塑性变化规律,在6 kN·m紧扣扭矩下,API接头已经达到屈服极限,与API钻具接头相比,高抗弯钻具接头抗扭性能提高约10%。
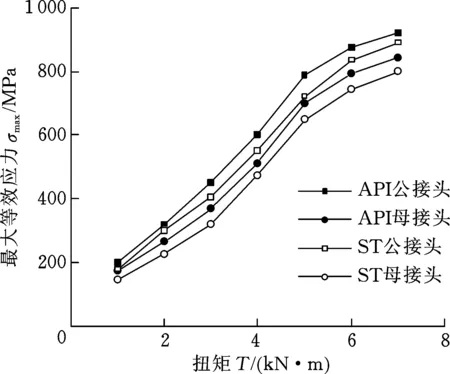
图17 API结构与ST结构抗扭性能对比Fig.17 Comparison of torque properties between API structure and ST structure
4.3 抗弯性能对比

图18 API结构与ST结构抗弯性能对比Fig.18 Comparison of bending properties between API structure and ST structure
对比计算高抗弯钻具接头与API钻具接头在弯曲载荷作用下的最大等效应力,结果如图18所示。可以看出,在弯曲载荷作用下,两种钻具接头中公扣最大等效应力均大于母扣承受的应力,且弯曲载荷相同时,与API钻具接头相比,高抗弯钻具接头抗弯性能提高15%,减少了因造斜率过高而导致的螺纹失效事故。为了研究高抗弯钻具接头在弯曲载荷作用下的密封特性,对比计算紧扣扭矩作用下两种钻具接头的接触压力特征,考虑到仅对螺纹参数进行正交优化,因此,分析第一圈及最后一圈螺纹牙啮合面接触压力变化情况,如图19所示。可以看出,第一圈及最后一圈螺纹牙接触压力变化较均匀,虽然弯曲载荷作用时螺纹牙一端受压一端受拉,但此时第一圈及最后一圈螺纹牙接触压力并未受到剧烈影响,且接触压力变化幅度较小,表明螺纹牙啮合面密封良好,且均未达到材料的屈服极限。与API钻具接头相比,高抗弯钻具接头密封性能提高约11%。
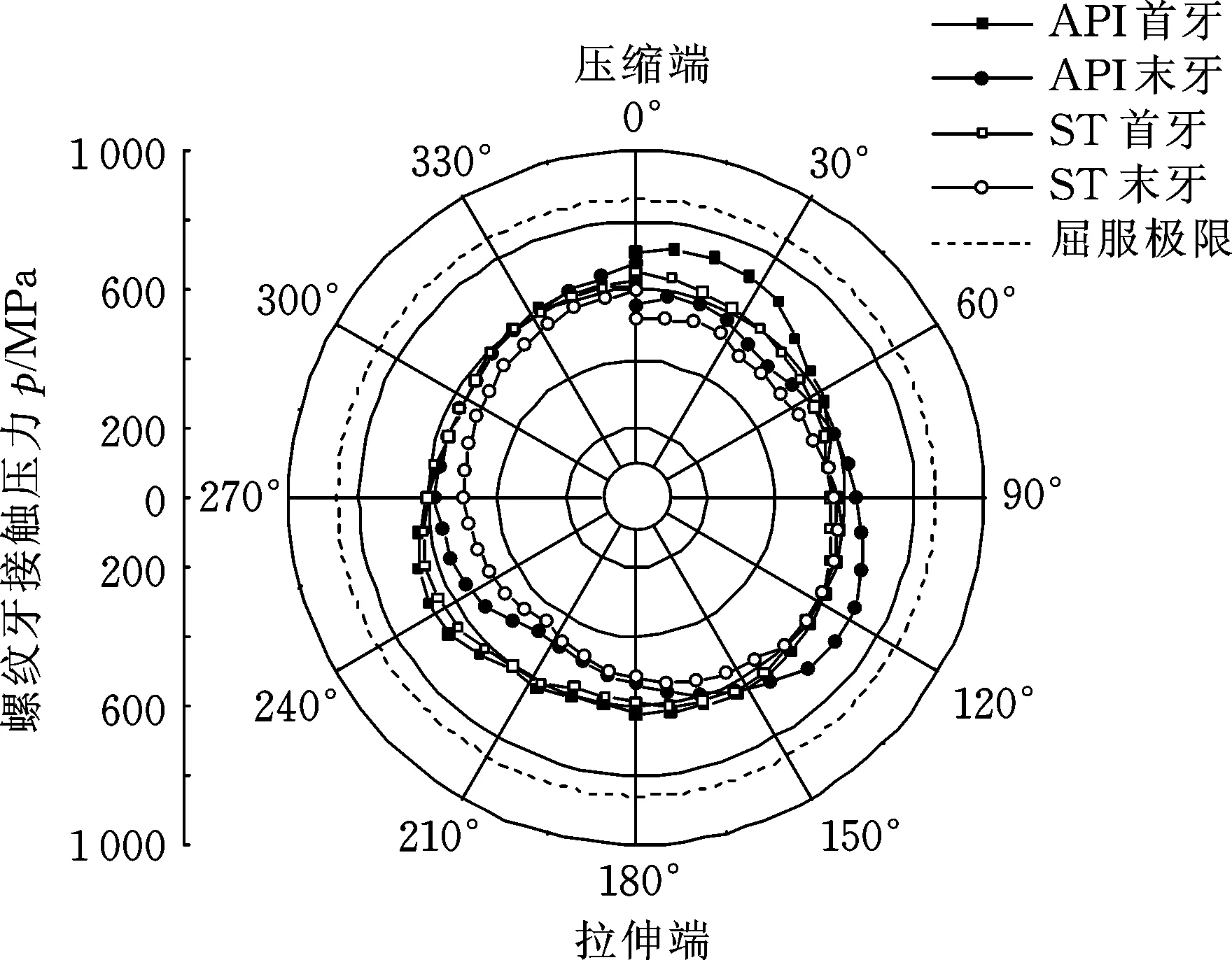
图19 API结构与ST结构密封性能对比Fig.19 Comparison of sealing performance between API structure and ST structure
5 结论
(1)本文基于钻具接头受弯时弹塑性关系,利用正交优化试验方法,综合考虑连接螺纹在井下的连接强度和密封性能,设计了一种高抗弯钻具接头,该钻具接头在满足抗拉/压、扭矩性能前提下可提高抗弯性能。得出各因素对抗弯性能影响的主次顺序分别为螺距、导向侧角度、承载侧角度及锥度。经正交优化方法计算出各弯曲载荷下各关键结构参数的较优组合,分别为:锥度1∶10,螺距7牙/英寸,承载侧角度20°,导向侧角度14°。
(2)对比计算了API钻具接头和ST高抗弯钻具接头在拉/压、扭矩、弯曲作用下的应力,其等效应力满足材料的弹塑性变化规律,且在外载荷作用下连接强度以及密封性能方面,高抗弯钻具接头均优于常规钻具接头,表明设计的高抗弯钻具接头能有效地满足小井眼开窗侧钻的钻井条件。
