钢坯拉速模糊信息粒化及钢坯定重切割的极限学习机预报
2020-01-03王福斌潘兴辰孙宇舸郭宝军
王福斌 潘兴辰 孙宇舸 郭宝军
1.华北理工大学电气工程学院,唐山,0632102.东北大学信息科学与工程学院,沈阳,1108193.北京交通大学海滨学院电子信息与控制工程系,沧州,061199
0 引言
钢坯连铸过程中,既有定尺切割又有定重切割生产工艺。为了与后续的棒材生产工艺相衔接,大多采用定重切割。在钢坯切割中,若定重精度不高,反而会影响后续棒材轧制成品率。如轧制长8 m规格的棒材时,若最后一根棒材轧制后尺寸为7.5 m,则视为不合格产品,不仅使钢坯材料利用率降低而且增加了能耗。因此,连铸钢坯定重预报精度是影响棒材轧制成材率、降低钢坯原材料浪费、减小能耗及环境污染的关键因素。
影响钢坯定重的因素较多,主要有钢坯拉速、切割机响应速度、钢水温度、钢坯定尺测量精度等。在众多因素中,钢坯拉速是影响钢坯截面变化的主要原因。由于钢坯截面的变化,往往导致以定尺为基准进行钢坯切割时,会使钢坯质量出现较大偏差。本课题组对连铸机的某一特定的钢流进行跟踪实验,针对每一根钢坯进行钢坯拉速、质量、长度等参数的测量,并连续测量182根钢坯生产工艺参数,对实验数据进行分析,结果表明,拉速是影响钢坯质量的主要因素。本文将拉速时间序列数据作为特征变量进行钢坯质量预报研究。由于每根钢坯的拉速数据量较大,故用模糊信息粒化方法对拉速样本数据进行特征提取,得到含不同信息的钢坯拉速数据粒化子集。通过构建基于拉速信息粒化数据的支持向量机(SVM)预报模型,获得钢坯平均拉速预报值[1-2]。最后结合其他工艺参数,采用极限学习机(ELM)神经网络实现钢坯定重的预报。将得到的钢坯切割质量预报数据作为控制决策依据,实时控制火切机的切割动作,完成对钢坯的定重切割。
1 钢坯工艺参数的测量及钢坯拉速分析
钢包中的钢水通过水口流入中间包,中间包中的钢水通过结晶器形成坯壳,再经过水冷拉坯最终形成小方坯、板坯等轧材,钢坯连铸工艺如图1所示。在钢坯生产过程中,需测量的工艺参数有钢水温度、钢坯拉速及钢坯定尺切割长度等。
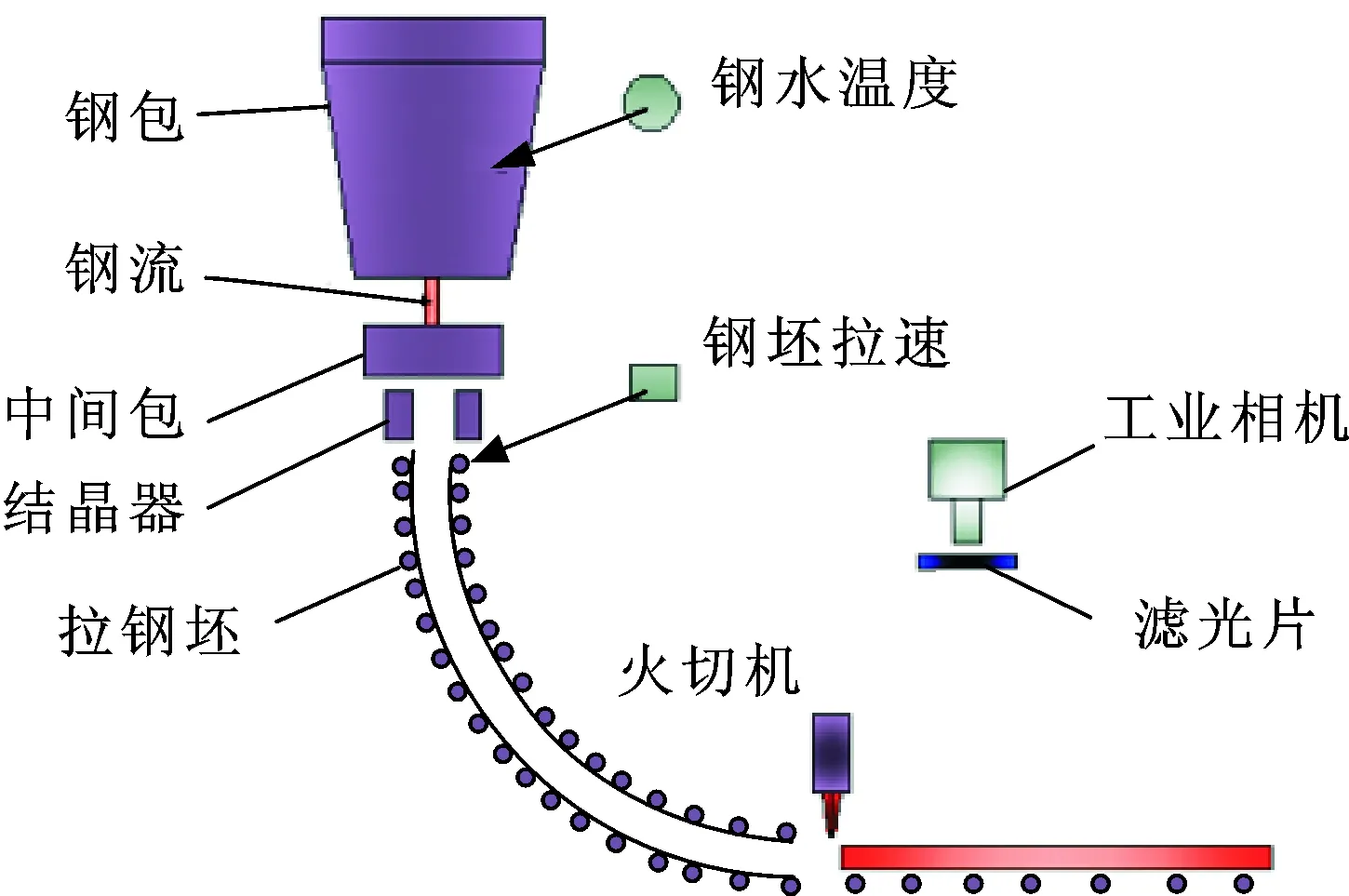
图1 钢坯连铸工艺过程Fig.1 Process of billet continuous casting
钢坯长度的测量采用图像测量方法,以实现非接触测量。在钢坯长度测量过程中,由于钢坯没有完全冷却,因此导致钢坯图像出现红色光晕现象。为此采用滤光片滤除光晕干扰,同时利用钢坯与背景之间的灰度差来减弱背景图像的干扰。
在进行钢坯长度的图像测量时,仍采用滤光片进行滤光处理。由于钢坯温度远小于钢水温度,故其光晕现象有所减弱,经滤光片滤光后钢坯与背景反差明显,更利于钢坯图像的分割,如图2所示。无滤光片时,钢坯图像背景较复杂,不利于钢坯目标图像的分割;采用滤光片后可明显滤除背景的干扰,对滤光后的钢坯图像分割效果较理想。

(a) 无滤光片图像

(b) 加滤光片图像

(c) 钢坯分割结果
在某型号连铸钢坯生产中,钢坯定尺长度为11.9 m。但在相同的钢坯长度下,会出现钢坯质量波动的现象。本课题组通过对182根钢坯进行连续测量,分析发现钢坯质量及其对应的长度处于经常变动中,多数原因是钢坯拉坯过程中拉速的波动。选取钢坯长度差在5 mm以内的两组钢坯,其中11 733 mm长的钢坯3根,11 738 mm长的钢坯7根,钢坯主要测量工艺参数见表1。在5 mm钢坯长度误差范围内,钢坯长度误差对钢坯质量的影响程度较弱,重点分析钢坯拉速与钢坯质量之间的关系。

表1 钢坯主要工艺参数
表1中,平均每根钢坯的拉速数据采集点数为360,钢坯的平均质量为2 439.89 kg。由表1中的数据可知,拉制钢坯时若平均拉速越高,则在大致相同的钢坯长度条件下钢坯的质量有减小的趋势,小于平均质量水平,如图3所示。平均拉速增大时,可导致钢坯截面呈变小的趋势,无法保证165 mm×165 mm截面的严格尺寸,并使得钢坯质量减小。这说明钢坯的平均拉速是影响钢坯质量较重要的因素之一。
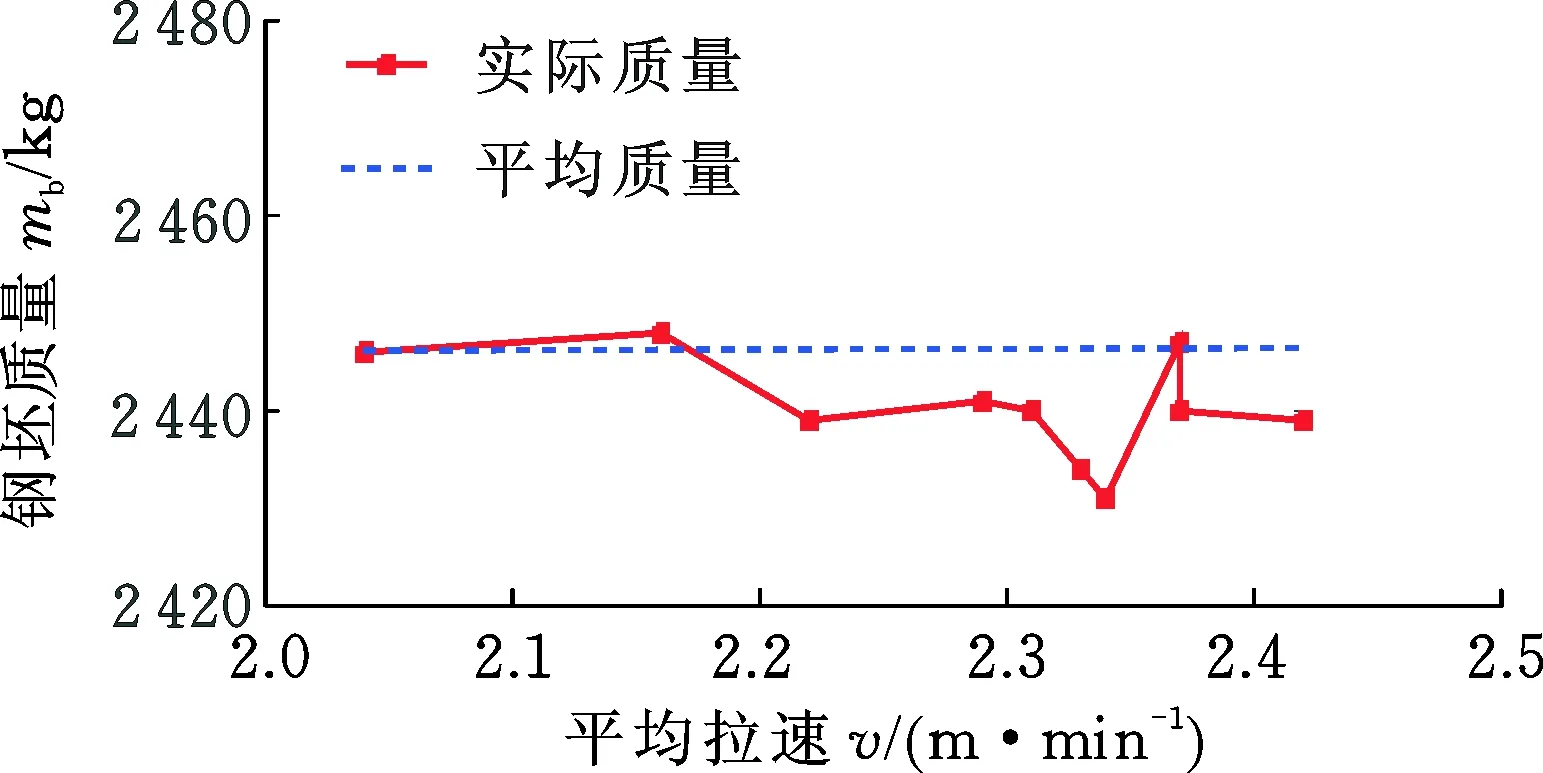
图3 钢坯质量随平均拉速的变化关系Fig.3 The relationship between the qualityand the average casting speed of steel billet
采用多项式最小二乘非线性拟合法,对表1中的10根钢坯的质量与平均拉速间的关系进行拟合,结果如图4所示。从拟合曲线的变化过程看出,随着钢坯平均拉速的变化,与之对应的钢坯质量也发生大致相同趋势的变化,说明采用平均拉速作为钢坯定重预报的主要参数是可行的。

图4 钢坯质量与平均拉速的最小二乘拟合Fig.4 Least squares fitting between the qualityand the average casting speed
2 钢坯拉速的模糊信息粒化
分析表明,钢坯平均拉速与钢坯质量之间存在一定的内在关联性。由于钢坯拉速数据量巨大,为有效提取有用的拉速信息进行钢坯质量预报,本文提出了模糊信息粒化与支持向量机相结合的钢坯平均拉速回归预报策略,用模糊信息粒化方法对钢坯拉速数据进行特征提取,进而用支持向量机对下一根钢坯平均拉速进行预报。
信息粒化的模型主要基于以下3种理论:模糊集理论模型、粗糙集理论模型和熵空间理论模型。本文采用基于模糊集理论的粒化模型对拉速时间序列数据进行模糊粒化。提取钢坯的平均拉速数据,将连续的每5根钢坯平均拉速数据通过划分窗口及模糊化处理,得到模糊粒子中的3个参数:平均拉速变化的最小值vlow、平均拉速变化的均值vmid和平均拉速变化的最大值vup,基于SVM模型实现对下一根钢坯平均拉速的预报[3]。
钢坯拉速数据可看作时间数据序列X={x1,x2, …,xn},粒化处理时,将数据序列X看作一个单窗口进行模糊化,采用三角型隶属度函数A(x,a,m,b)作为模糊粒子[4-5],有
(1)
其中,x为论域中的变量,a为三角型模糊集支撑下界,b为三角型模糊集支撑上界,m为三角型模糊集的核参数。a=1.2、b=3.2、m=2.2时的模糊隶属度函数如图5所示。
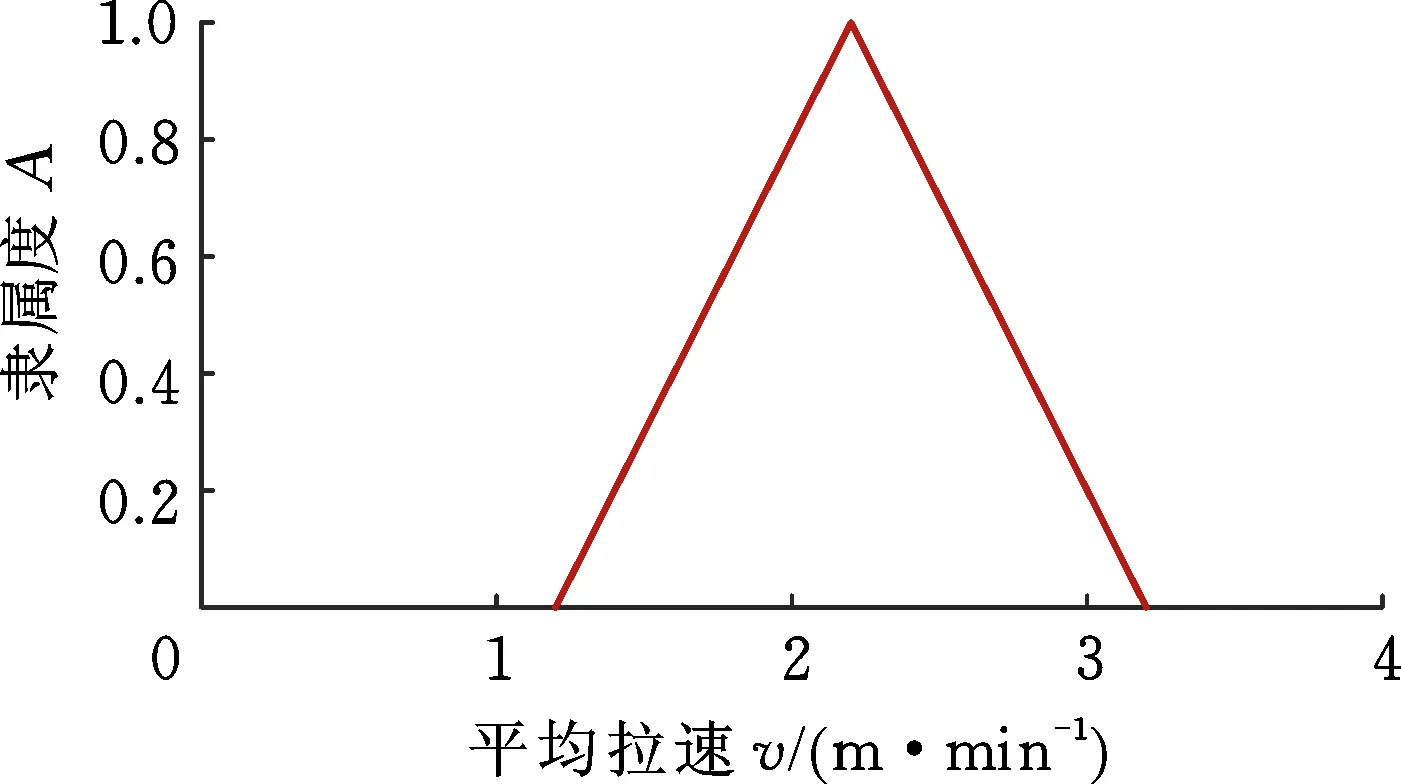
图5 三角形模糊集Fig.5 Triangular fuzzy set
以钢坯拉速时间序列数据作为输入,将每5根钢坯各自的平均拉速数据划分为一个窗口,按从小到大排列,得到X={x1,x2, …,x5},将其粒化为一个模糊输出粒子:钢坯平均拉速变化的最小值vlow、平均拉速变化的均值vmid和平均拉速变化的最大值vup,分别对应三角型隶属度函数A(x,a,m,b)中的a、m、b三个参数。粒化过程采用Witold Pedrycz模糊粒化算法,其核心思想如下:
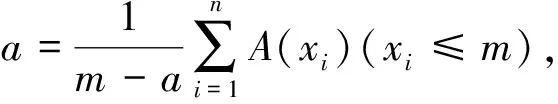
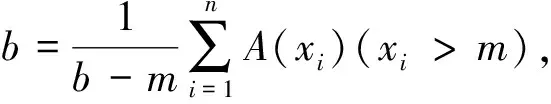
(3)将X={x1,x2, …,xn}中的元素按小到大的顺序重新排序。当n为偶数时,m取X中间元素的值;当n为奇数时,m取X中间两个元素的算术平均值。
(4)输出粒化后的模糊粒子P(a,m,b)。
3 基于信息粒化的钢坯平均拉速SVM预报
支持向量机(SVM)通过将输入向量映射到一高维特征空间,实现模式分类及非线性回归问题的求解。本文通过拉速数据的时间轴粒化,与SVM相结合建立时间序列的非线性预测模型[6]。
钢坯平均拉速SVM回归预报模型实现过程如图6所示,模型的核函数选用径向基核函数。模型的输入向量为钢坯平均拉速变化的最小值vlow、平均拉速变化的均值vmid和平均拉速变化的最大值vup。拉速数据信息粒化的时间窗口长度取5,即将每5根钢坯的平均拉速数据变换为一个三角型模糊粒子[7-10]。
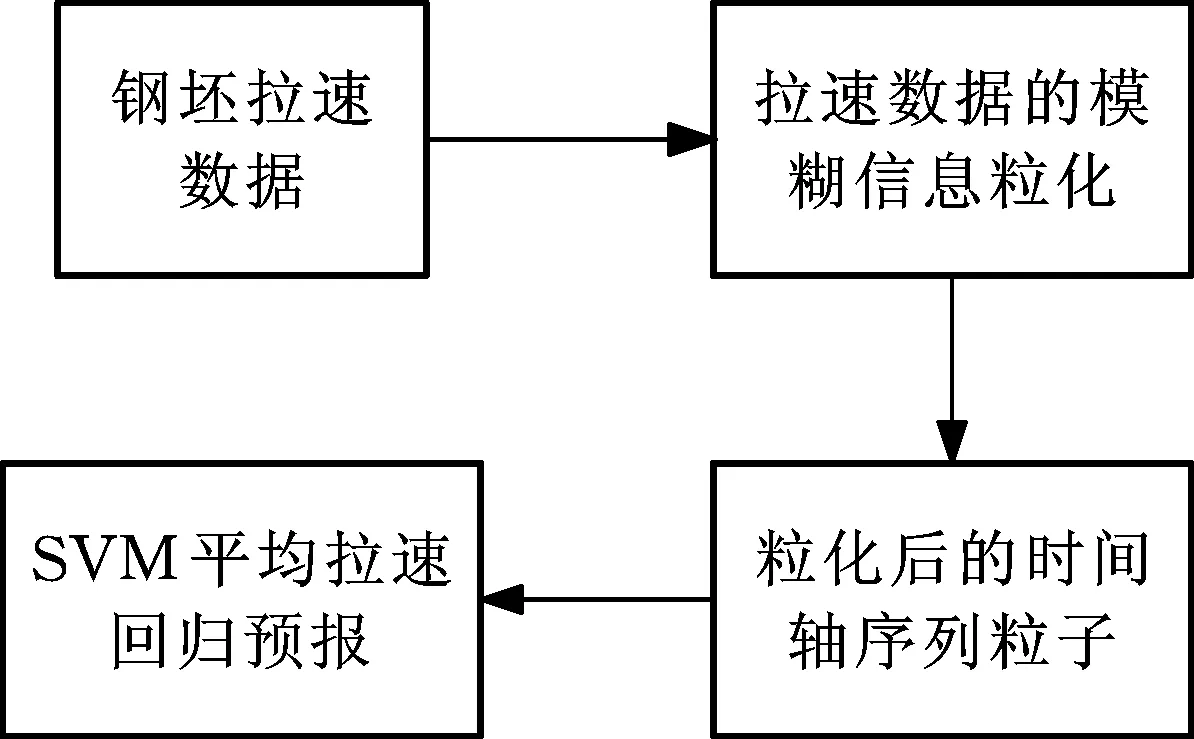
图6 基于拉速信息粒化的SVM回归预报Fig.6 SVM regression forecasting based on information granulation of casting speed
钢坯拉速数据的模糊信息粒化过程主要为窗口划分和模糊化过程,进而得到以模糊集形式表示的信息粒。窗口化按照钢坯拉速变化的时间序列,将每5根钢坯的平均拉速数据作为一个子序列;模糊化按照三角型隶属度函数,将一个窗口内的拉速数据变换为模糊粒子。
选择粒化窗口为5,对连续的125根钢坯进行粒化处理,使用时间序列三角形模糊信息粒子实现的拉速粒化结果如图7所示。
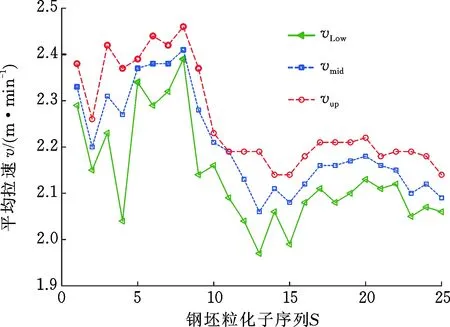
图7 连续的125根钢坯拉速信息粒化结果Fig.7 Information granulation results for casting speed of continuous 125 steel billets
将粒化后的数据作为输入量,下一根被预测的钢坯平均拉速作为输出量,构建训练样本。选取60根钢坯做粒化处理,构建的部分训练样本见表2。
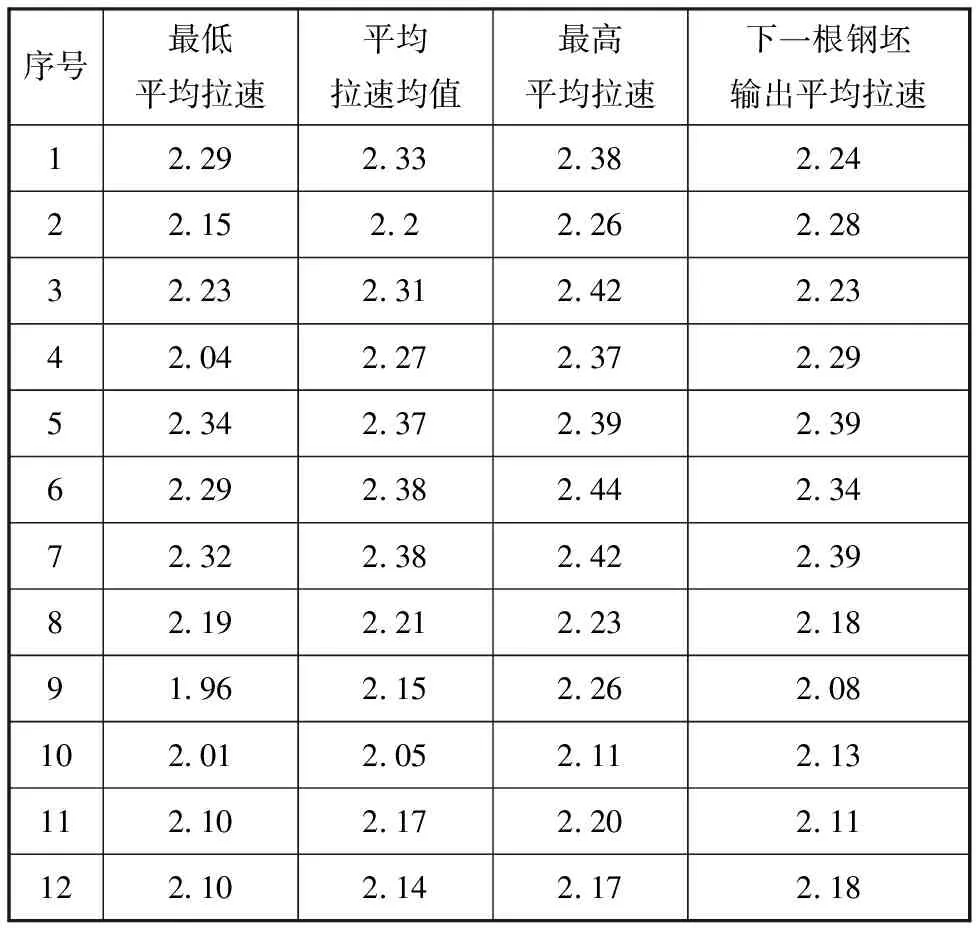
表2 钢坯平均拉速的SVM回归预报训练样本
用表2中的粒化数据对SVM回归模型进行训练,选取4组样本进行测试,经测试得到的平均拉速预报输出结果见表3。
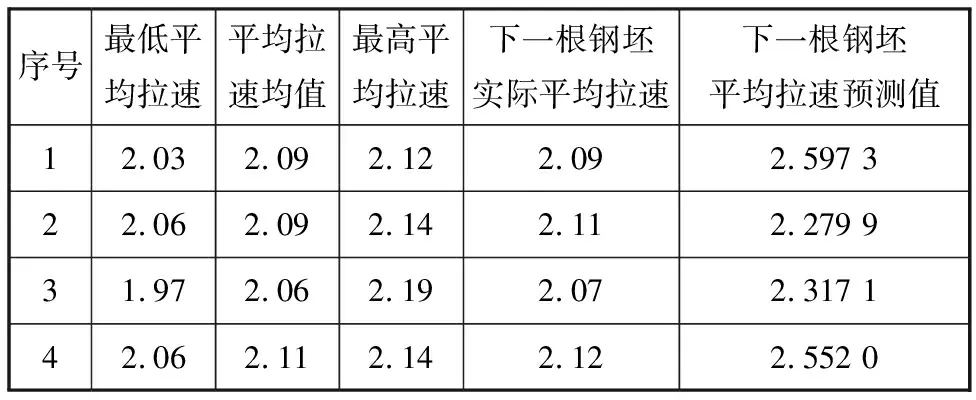
表3 SVM平均拉速预报结果
平均拉速的预报输出与实际输出对比如图8所示。由于样本数量有限,故平均拉速预报输出有一定的误差,若加大训练样本数量,预测精度会得到提高。

图8 钢坯平均拉速对比曲线Fig.8 Contrast curve of average casting speed of steel billets
4 ELM神经网络钢坯定重预报
4.1 ELM原理
传统的前馈型神经网络迭代过程采用最速梯度下降法更新权值和阈值,具有局部极值及泛化性能不佳等固有的缺陷。Huang等基于摩尔-彭罗斯(MP)广义逆矩阵理论提出了极限学习机(ELM)算法,与传统迭代算法相比,ELM采用单步计算解析求出网络的输出权值,极大地加快了网络学习速度[11-12]。ELM网络训练模型采用单隐层前向网络结构,如图9所示。
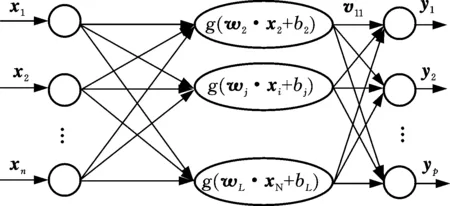
图9 ELM网络结构Fig.9 The network architecture of extreme learning machine
图9中,输入层、隐层和输出层的节点数分别为n、L、p;隐层神经元的激活函数为g(x),隐层单元阈值为bi。对于由N个输入及输出数据集构建的样本{(xi,yi)|xi∈Rn,yi∈Rn,i=1,2,…,N},通过L个隐层神经元获得的网络输出值
(2)
i=1,2,…,Nj=1,2,…,L
wj=(w1j,w2j,…,wnj)vj=(vj1,vj2,…,vjp)T
oi=(oi1,oi2,…,oip)T
其中,wj、vj分别为与第j个隐层节点相连接的输入权值向量和输出权值向量。极限学习机的寻优代价函数见文献[13-14],寻优代价函数中的广义逆矩阵见文献[15-17] 。
4.2 ELM神经网络钢坯定重预报
极限学习机钢坯质量预测模型训练样本见表4。训练样本的输入向量如下:钢坯截面积、钢坯平均拉速、定尺长度、下一根钢坯平均拉速预测值;输出向量为下一根钢坯质量。
实际运行时,训练及测试样本中的输入向量均做了归一化处理。采用表4中的归一化样本数据对ELM模型进行训练后,使用表5中的测试样本数据对ELM神经网络预报性能进行测试,钢坯质量预报结果见表5中最后一列。将预测质量与钢坯实际质量进行对比,表明ELM模型的预报结果具有较高的准确度。
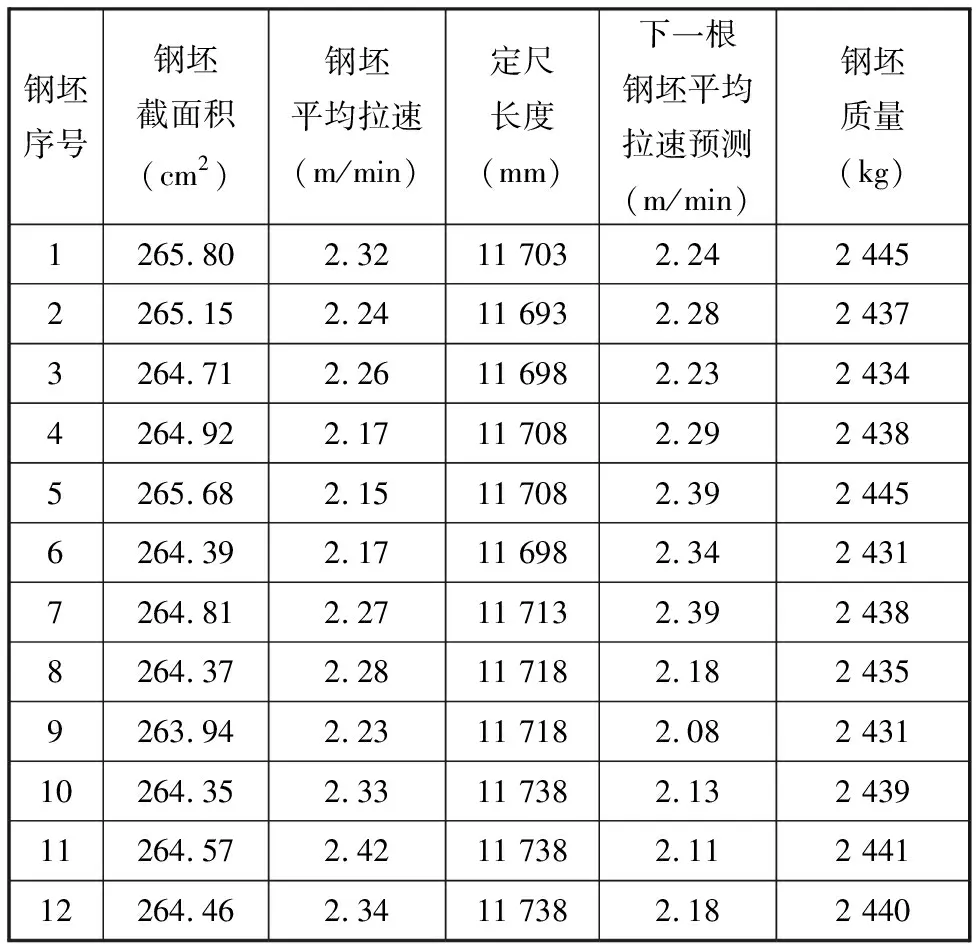
表4 基于ELM的钢坯定重训练样本
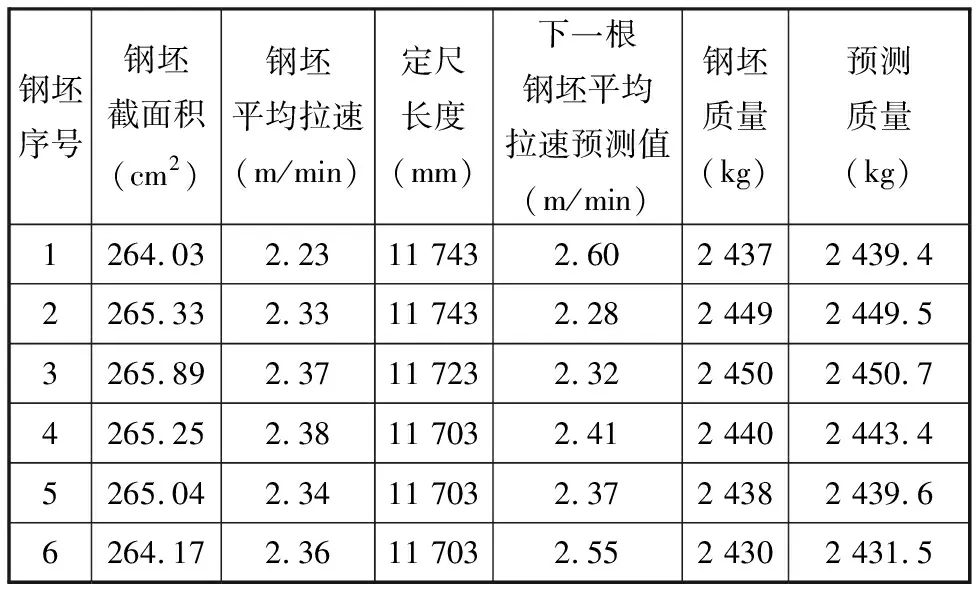
表5 ELM钢坯定重预报结果
为进一步比较ELM神经网络与传统的BP神经网络的预报性能,在同一组训练及测试样本条件下对BP网络预报性能进行测试,结果如图10所示。从预报结果看出,ELM神经网络的预报精度更高。
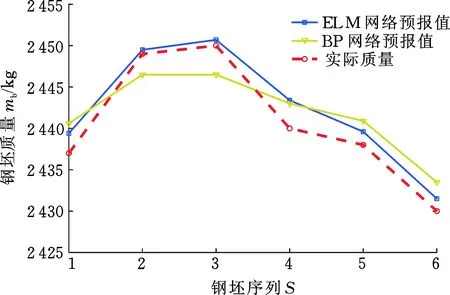
图10 ELM与BP神经网络预报结果比较Fig.10 Comparison of prediction results between ELM and BP neural network
5 结论
本文通过对连铸机钢坯生产过程的跟踪,采集大量的过程参数,定性分析了钢坯平均拉速与钢坯质量的关系。由于每根钢坯的拉速采集点数较多,故采用信息粒化模型对钢坯拉速进行模糊粒化处理,实现了基于拉速粒化数据的SVM钢坯平均拉速预报。通过结合拉速预报值及其他工艺参数,进一步实现了钢坯定重的ELM预报。对训练样本及测试样本的实验结果表明,本文提出的钢坯定重预报方法是有效的。若加大训练样本数量,会进一步提高预报精度。
