连续切换正系统的稳定性分析与L1增益控制

黄丽琼

（商洛学院 数学与计算机应用学院，陕西商洛 726000）

切换正系统是由有限个正系统和一个切换信号组成，其中切换信号协调各子系统之间的运行，切换正系统在网络、经济学及人口模型等要求状态模型为非负的领域内应用非常广泛[1-3]。近几年来对于切换正系统的稳定性问题研究结果非常多[4-6]，同时对于切换正系统，信号向量的绝对值之和具有一定的物理意义，因此对正系统进行L1增益分析是很有必要的。文献[7]利用线性余正Lyapunov 泛函给出双时滞线性切换正系统是指数稳定的且具有抑制干扰能力γ 的充分条件，文献[8]提出了一种时变分段定长线性Lyapunov 函数方法，给出了离散线性切换系统渐进稳定性的充分条件，并利用此方法得到系统的L2增益分析。文献[9]利用文献[8]中的时变分段定长线性Lyapunov 函数，给出了离散正切换系统的稳定性条件，同时利用线性矩阵不等式方法求解使系统渐进稳定的最小驻留时间。

本文主要将文献[8]中的方法推广到连续正切换线性系统中，借助时变分段余正Lyapunov 函数方法，得到一个带驻留时间约束的连续线性切换正系统稳定性的充分条件，并进一步利用此方法给出系统具有L1增益的充分条件。文中符号说明：Ai≻0（Ai≥0，Ai≺0）表示矩阵Ai中每一个元素都是正（非负，负）的表示由所有元素都是非负的n 维向量组成的集合，‖x‖1表示向量1-范数，‖x‖=表示向量的L1范数。

1 预备知识

本文主要考察如下一类连续时间切换正系统：

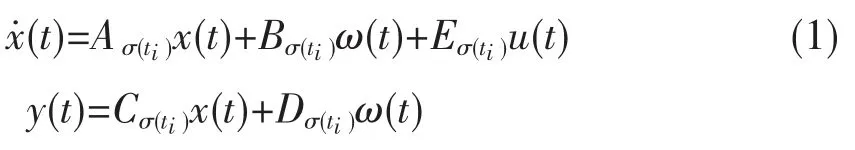
引理1[9]系统(1)为正系统，当且仅当下列条件成立

1）系统的初始状态x(0)非负。

2）Ai为 Metzler 矩阵，即 Ai的所有非对角元素全是非负的，Bσ(ti)，Cσ(ti)，Dσ(ti)，Eσ(ti)，i∈N 均为相容维数的非负矩阵。

定义1对任意切换信号σ(t)，假设σ(t)对应的切换序列为 t0,t1，…，tk，…，k∈N+，如果存在常数 t*满足则称 t*为系统(1)的最小的驻留时间。

定义2给定常数γ＞0，称系统(1)有一个标准L1增益，如果下列两个条件满足：

1）当 ω(t)=0，u(t)=0 时，系统(1)是渐进稳定的。

2）在零初始状态下，系统(1)满足

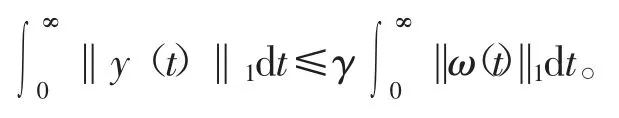
定义3若系统(1)满足初始状态且是渐进稳定的，那么对任意的切换信号σ(t)，都有‖x(t)‖→0(t→∞)。

2 主要结果

定理1考虑连续切换正系统(1)，其中ω(t)=0，u(t)=0,给定一个标量 d＞0，假设存在一系列的向量 λi,m,m=0,1,…,d-1，i∈N 使得下列条件成立：

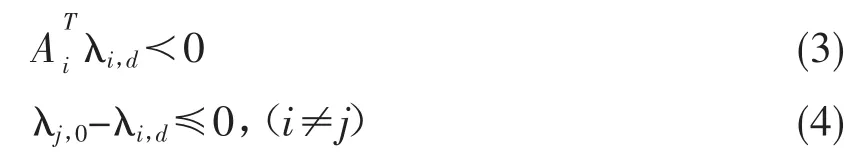
那么系统(1)在满足如下条件的切换信号下，是渐进稳定的。

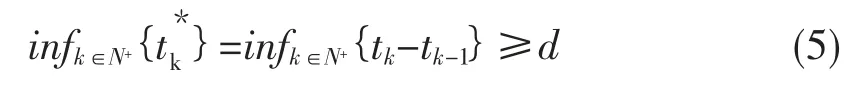
证明取Lyapunov 函数如Vi（x(t)）=x(t)Tλi(t)，其中

λi（t）在区间[tn,tn+d)上为时变向量λi,m，在区间[tn+d,tn+1)为不变常值 λi,d，假设系统(1)的切换序列为 t0，t1，…,tk,…，k∈N+，在区间[tn,tn+1)上第i 个子系统被激活，即σ(ti)=i，由于最小驻留时间为d,那么驻留时间区间被分成了两部分。

当 t∈[tn,tn+d)时，从式(2)可以得到

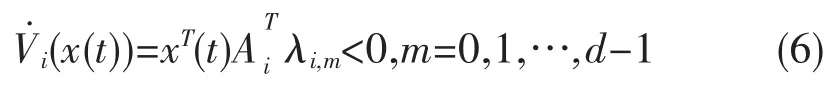
当 t∈[tn+d,tn+1)时，由式(3)得

假设在时刻tn，系统从第i 个子系统切换到第j 系统，从式(4)

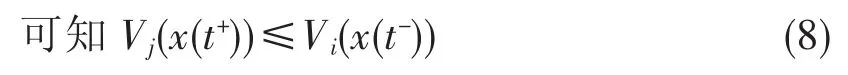
由式(6)(7)(8)可以知道函数Vσ(t)x(t)随着时间趋向于无穷最终收敛到零，从而说明系统（1）在切换信号(5)下是渐进稳定的。

定理2考虑连续时间切换正系统 (1)，其中 u(t)=0，给定一个标量 γ＞0,d＞0，如果存在一系列的向量λi,m,m=0,1,…,d-1,i∈N 使得下列条件成立：

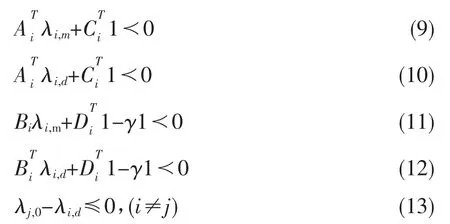
那么连续时间切换正系统(1)在ω(t)=0 的条件下为渐进稳定的，并在如下切换信号下有一个不超过γ 的标准L1增益表现系数。

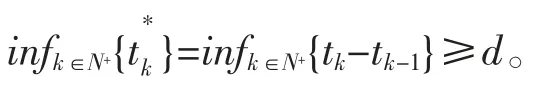
证明令ω(t)=0，根据定理1 可得到系统是渐进稳定的，下面主要证明系统的L1增益性。

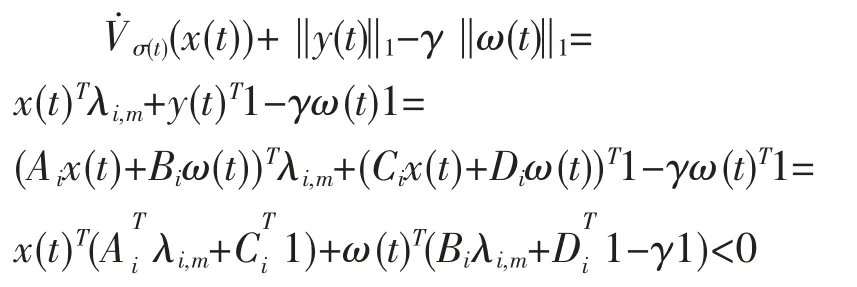
当t∈[tn+d,tn+1)时，相似的可以得到

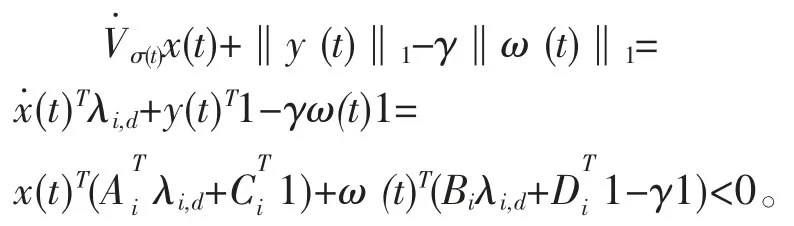
由式(10)(12)Vσ(t)x(t)＜-(‖y(t)‖1-γ‖ω(t)‖1)，t∈[tn＋d,tn＋1)。

由上述两部分证明结果可得出

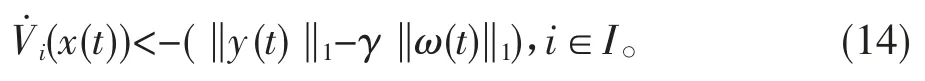
通过式(13)，可得

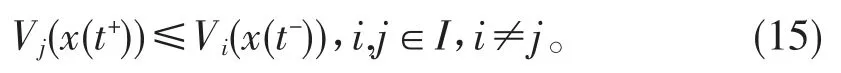
对区间[t0,t]，对式(14)两端进行积分得

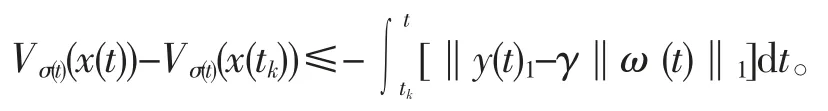
由式(15)可得

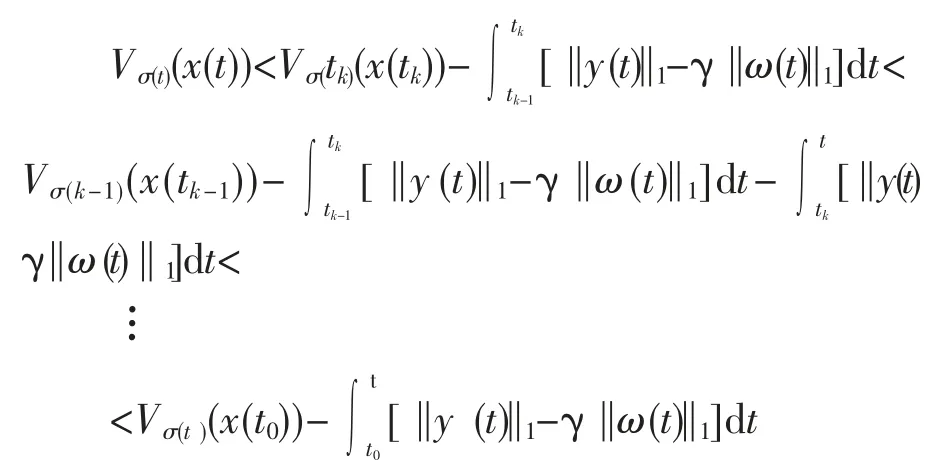
在零初始条件下，当t→∞有

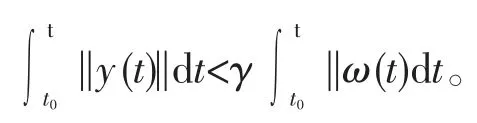
3 结论

本文讨论了带有驻留时间约束的切换正系统的稳定性，给出了使所讨论的系统在渐进稳定所容许的最小驻留时间的求解方法，同时把此方法推广到切换系统的L1增益分析中，给出了驻留时间与γ-L1增益之间的关系。