无界区域上一类拟线性外问题的耦合法
2020-01-02姚雪春
黄 姗,姚雪春
(南京财经大学 应用数学学院,江苏 南京 210023)
科学和工程计算中的许多实际问题,如电磁波的辐射与绕射等问题都可以归结为无界区域上偏微分方程边值问题[1-2]。用数值方法求解该问题可以通过引入人工边界来解决。冯康和余德浩教授首创并发展了自然边界元方法[3],由此产生了很多有效的方法,如自然边界元与有限元耦合法[4-5],DtN 交替算法[6,20-21],区域分解算法[7-8,18-19]等。 对于用耦合法求解方形或凹角裂缝外区域问题,常选取圆或圆弧作人工边界[9-10],但在求解“凹角椭圆形或凹角长条形区域[11]”内边界的外问题时,以圆弧作人工边界显然不是最佳选择,它会导致求解区域过大,从而产生一些不必要的计算,甚至得到令人不满意的数值结果。 所以,本文将给出求解一类具有凹角长条形内边界的拟线性方程[9-10,16]外问题的耦合法。
设Ω 为带凹角的长条形无界、简单的连通区域的外部,并且有足够光滑的边界,∂Ω=Γ0∪Γα∪Γ,其中 Γ0={(r,0)│r≥a},Γα={(r,α)│r≥b},Γ={(r,θ)│r=φ(θ)≥0,0≤θ≤α,φ(0)=a,φ(α)=b},而 Γ 是一条光滑的曲线。其中 α 为凹角(图1),边界 Γ 随 Γ0和 Γα的改变而改变。

本文研究的问题如下

为研究需要,首先引入椭圆坐标的一些性质,对于平面上的点,其直角坐标(x,y)和椭圆坐标(μ,φ)满足如下关系:

其中f0为常数,cosh 和sinh 为双曲余弦和双曲正弦,当μ取不同正整数时,式(2)描述了平面内的一簇共焦椭圆。
对于问题(1)选取椭圆弧形人工边界,即以原点为圆心, 如图2 作椭圆弧 ΓR={(μ,φ) │μ=μR,0≤φ≤α},且dist (Γ,ΓR)>0, 这样 ΓR将区域 Ω 分成两个子区域 Ωi和Ωe, 其中 Ωi为 ΓR,Γ,Ω0i,Ωαi围成的有界区域,Ωe为 ΓR,Γ0e,Γαe以外的无界区域。
上述的 α(x,u),β(x,u)满足的要求如下:


3.对∀u,v∈R 以及几乎所有的 x∈Ω,存在常数 CL>0,使得

定理1[12]变换(2)有如下性质:1.变换的Jacobi 行列式为

J(μ,φ)当且仅当(x,y)=(±f0,0)。
2.对于 u∈C2(R2),成立


1 精确的人工边界
在区域Ωe上有由 Kirchhoff 变换[13]得

所以

Ωe上的问题转化为

由分离变量法,可得Poisson 积分公式
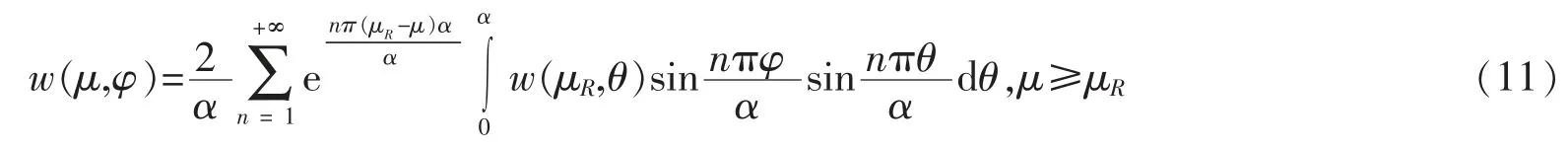
自然积分方程

由(9)

由(9)和(12)可得ΓR上的精确的人工边界条件

从而,Ωi的问题转化为

其中 Γ0i=Γ0∩Ωi,Γαi=Γα∩Ωi。 因此,问题(1)的解等价转化为求解问题(15)的解。
2 有限元逼近
2.1 等价变分问题
对于问题(15),引入Sobolev 标准的空间Wm,p。 ‖·‖和│·│分别参照相应范数和半范数定义,定义

问题(15)的解空间为

相应范数

问题(15)等价于如下变分问题:求u∈V,使得

根据文献[9],[14],对∀s∈R,在 Sobolev 空间中定义 Hs(ΓR)如下
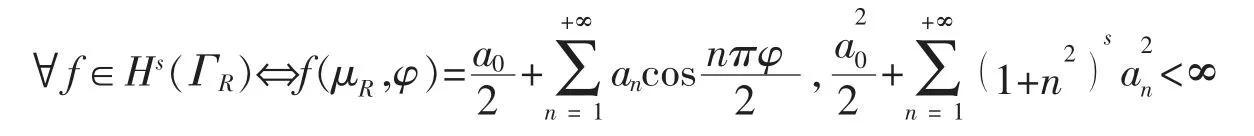
同时定义 Hs(ΓR)上的范数为

证明:令

则

由式(4)、Cauchy-Schwarz 不等式及迹定理有

考虑问题Ωe上的等价问题

并且问题(20)的解 u 满足

代入(19)整理得
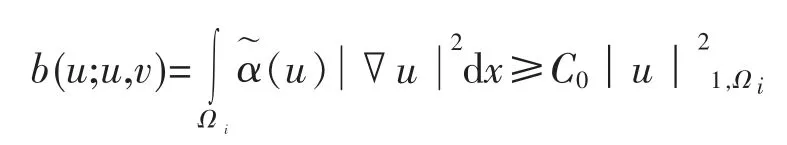
此外,对∀N∈N*,(14)式的前 N 项和记为

其中

可得问题(15)的如下近似

问题(23)的等价变分问题为
求 uN∈V,使得

其中

类似地,有
引理 2∃C>0,使得

2.2 有限元方法逼近
采用有限元剖分将区域Ωi分割成一系列规则的三角形单元ζh,使得

其中K 是一个曲边三角形,h 是三角形的最大直径。 令

问题(24)可转化为

与文献[15]中引理6.1 类似,有
引理 3问题(17)、(24)以及(28)的解是存在且唯一的。
2.3 收敛定理

设 {Vh}h→0是有限维空间 V∩C(Ωi)的子空间,并且满足

并且对

其中 C(v)>0 与 h 有关。

根据文献[15-16]中的收敛定理,得到

此外,可以得到下面的结果。
引理 4如果,u分别是(24)和(17)的解,那么有

证明 由(4)、(25)和引理 2,有

由 μ>μR以及在 V 中有界,于是存在的子列使得同文献[9]中引理 3.4 的证明可得式(33)。
综上得到以下结果。
定理 2令 u∈H2(Ωi)并假设其满足(29)-(31),则
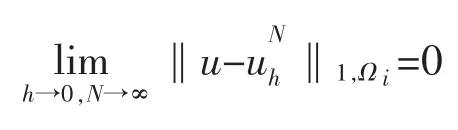
3 数值例子
设外区域Ω(如图3)由如下边界组成
Γ0={(r,0)│r≥a},Γα={(r,α)│r≥b},Γ={(r,θ)│r=φ(θ)≥0,0≤θ≤α,φ(0)=a,φ(α)=b}
考虑如下问题


令β=0,边界条件为

取人工边界 ΓR={(μ,φ)│μ=1.5,0<φ<α},其中
非线性项为

精确解为

区域剖分和数值结果如图4-5。
网格剖分,分别采用的是 2×9,4×17,8×33(见图4),16×55;图5 给出了人工边界上随着剖分的加密(分别有9,17,33,65 个节点)绝对误差的变化趋势;实验中,采用线性插值基函数,表1 表明,随着剖分的加密,得到的自然边界元与有限元耦合法具有线性的收敛速度。

图4 mesh=8×33
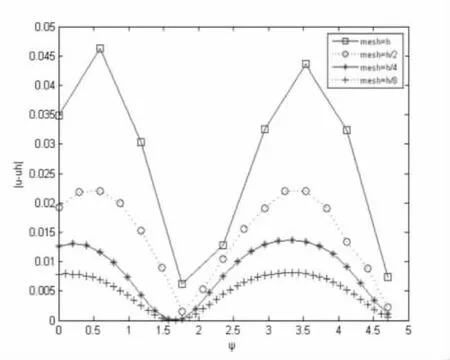
图5 不同网格下人工边界ΓR上的误差比较

表1 L2 和L∞范数下不同网格的误差比较
4 结论
文章主要运用自然边界元与有限元耦合法研究了椭圆凹角区域上的拟线性问题。首先依据自然边界归化得到了椭圆弧人工边界上的精确人工边界条件,然后给出了相应问题解的收敛性分析,最后给出了相应数值例子。 数值例子表明,采用(27)的线性插值基函数,伴随着剖分细度的增加,误差具有线性收敛速度。 这也说明了,本文所给出的数值方法对上述类型区域是精确有效的。
