利用XGBoost和SVR算法的地铁站客流量模型研究
2020-01-02李蕙萱吴瑞溢
李蕙萱,吴瑞溢
(黎明职业大学 通识教育学院,福建 泉州 362000)
随着我国城镇化进程的加快以及城市道路交通问题的不断恶化,越来越多的城市将发展以地铁为主的城市轨道交通作为解决城市交通问题的主要手段[1]。 地铁具有节能环保、干扰少以及客流运输效率高等优点,是我国城市轨道交通中运用最广泛的铁路系统种类。 但是,我国目前也面临这因城市地铁建设起步较晚,地铁站客流量预测准确率低的问题,这会直接导致交通资源的浪费以及地铁运营管理的混乱[2]。 因此,对城市地铁客流量预测问题进行具有重要的现实意义。
在大数据时代,社会生活和发展的方方面面都在发生颠覆性的转变。 特别是在交通领域,因为交通大数据具有体量大、种类多、价值丰富等特征,其在智慧城市建设背景下,通过相互作用和关联为城市交通管理提供更大的可能,并且从以往杂乱无章的管理方式中解脱出来。 交通大数据应用的关键是数据关联性研究,即将城市交通与其它因素的相互关联属性挖掘出来,从而提高数据本身的应用价值[3]。 比如,天气状况因素和城市交通拥堵程度的具有直接相关性,通过利用大数据分析对交通数据进行处理,挖掘出两者之间的关系,从而为交通管理、引导和规划提供数据支撑,这也是本文研究基于大数据分析的城市地铁站客流量预测的出发点。
针对地铁站客流量预测的问题,相关学者进行了很多研究。 比如,包磊通过建立灰色模型和马尔科夫链来对列车下一站实际客流量进行预测,实时客流量预测准确率较高[4]。 唐秋生和程鹏等提出一种基于GSO-BPNN 算法的地铁站客流量预测模型,与BP 网络预测模型相比,GSO-BPNN 预测模型有更好的收敛速度和稳定性[5]。 熊燕采用多元线性回归法对节假日前北京轨道客运量进行预测,预测结果和真实值相比拟合度较高,但是线性回归算法没有考虑交互效应和非线性的因果关系,会对建模精度产生不利影响[6]。
黄廷辉等以时间、道路状况以及天气状况等特征参数为基础,通过建立DUTP-GBDT 模型来预测实时交通流,准确率较高[7]。 许敏等提出一种基于改进的支持向量机算法来对繁忙机场高峰航班流量进行预测,该算法在短期实时预测和长期趋势预测中都可以获得较高的预测精度[8]。 文中受此启发,分别采用基于XGboost(extreme gradient boosting)和支持向量回归机(support vector regression,SVR)预测模型,并利用天气状况等特征参数对某大城市地铁站客流量进行预测,借助交叉验证、高偏差拟合、高方差过拟合以及特征归一等方法对模型参数进行优化以提高预测准确率,最后通过计算机仿真验证算法有效性。
1 XGBoost预测模型
1.1 回归决策树
XGBoost 的全称为Extreme Gradient Boosting,是GBDT 的一种高效实现,其是由陈天奇博士提出的[9]。
GBDT 是一种迭代决策树算法,由多棵决策树组成,即所有决策树的累加结果就是最终解。 采用GBDT 解决回归预测问题首先要生成回归决策树,即递归地构建回归二叉决策树的过程,应用平方误差最小化原则[10]。
假设训练数据集合如式(1)所示

其中X 为输入变量,Y 为连续输出变量。
分别对应每个回归决策树特征空间的一个划分以及划分单元上的输出值, 回归树模型如(2)式所示

其中Rm是被划分的输入空间的每个单元,cm是代表每个单元上固定的输出值。
这里通过启发式方法对输入空间进行划分,选择第j 个变量x(j)和对应取值s 分别作为切分变量与切分点,并定义两个区域
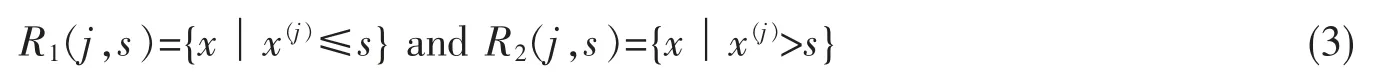
因为单元Rm上cm的最优值cmbest是Rm上所有输入实例xi对应输出yi的平均值,采用式(4)和式(5)寻找最优切分变量j 和最优切分点s。
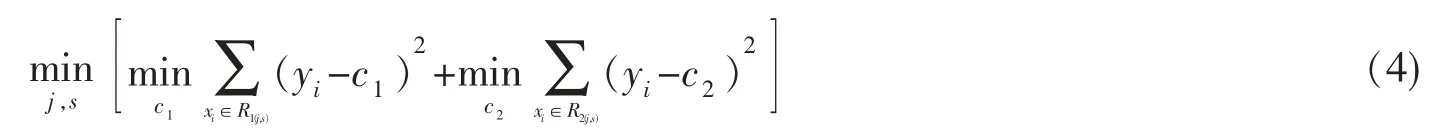

输入变量X,找到最优的切分变量j 以及对应的值s 构成(j,s),将输入空间划分为两个区域,按上述划分过程继续对每个区域进行划分。 当停止条件满足时,回归决策树生成完毕。
采用平方误差来表示回归决策树的预测误差,如式(6)所示,平方误差最小时对应每个单元的最优解。

1.2 梯度提升树算法
提升(boosting)方法是一种常用的统计学习算法,在数据挖掘中应用十分广泛且能取得较好结果,其迭代多棵决策树来共同决策。 因为本文讨论的是回归预测问题,所以提升树采用回归树作为基本分类器[11]。
回归提升树fM(x)采用如式(7)~(9)所示的前向分步算法得到。

其中,第m 步模型是由前一步模型fm-1(x)以及通过拟合残差学习的回归决策树叠加得到的残差采用式(6)的平方误差。 平方误差损失函数与当前模型拟合数据残差,分别如(10)式和(11)式所示,两式联立得到回归决策树,最后利用式(9)的加法模型即可得到回归提升树。
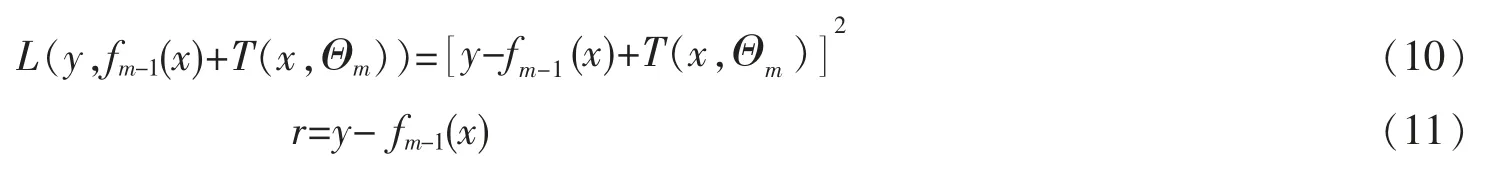
梯度提升算法(gradient boosting)可以简化优化过程,提高拟合速度。 Gradient boosting 是Freid-Man 在2000 年提出的,其利用的是当前模型中损失函数的负梯度值G 作为提升树算法中的残差的近似值,进而拟合一棵回归树[12]。

1.3 XGBoost算法
XGBoost 算法是在损失函数中加入正则化项,对整体求最优解后再以此权衡损失函数的下降和模型的复杂程度,从而避免过度拟合。基学习为决策回归树时,而正则化项与树的叶子节点的数量T与叶子节点的值有关。
在算法公式推导中,GBDT 只利用了一阶导数信息,而XGBoost 却对损失函数做了二阶的泰勒展开,其精度就更高。 XGBoost 在计算树节点分裂求增益的过程中做了如下三点改进:
(1) 在剪枝过程中,用阈值的设置来限制树的生成,
(2) 用系数的设置来对叶子节点值做平滑,防止过拟合;
(3)一种分裂节点寻找近似算法的实现,用于加速和减小内存消耗,即首先采取百分位法选取几个可能的分割点,然后从中根据计算公式找出最佳分割点。
2 SVR预测模型
2.1 SVR模型
支持向量机(SVM)通过将低维样本空间无法线性处理的样本集转化到高维特征空间中的线性超平面实现线性处理,并采用核函数的展开定理大大简化了计算复杂度,因而被广泛应用在分类、回归问题中。 SVR 是Vladimir N.Vapnik 在1996 年首次提出的,其是SVM 在回归问题应用分支。
SVR 采用了支持向量的思想,利用拉格朗日乘子式来对数据进行回归分析。 其中,支持向量(support vector)是训练数据集的样本点与分离超平面距离最近的样本点的实例。
假定一个特征空间的训练数据集

其中,xi∈X=Rn,yi∈Y={+1,-1},i=1,2,…,N, xi为第 i 个特征向量,yi为类标记。 转化低维的回归问题为高维特征空间,如(13)式和(14)式所示

式(13)表示回归函数和实际训练点之间的函数间隔,其表示回归预测的正确性及准确率。 将一定误差范围外的边界点作为模型确定的支持向量,范围内的点都作为模型上的点。 为了解决某些想本店不知能满足函数间隔不小于1 的边界条件的问题,引入松弛变量ζi≥0,同时对每个松弛变量支付一个代价,得到新的支持向量回归表达式,如式(15)和式(16)所示:

其中,式(15)中的C 为惩罚参数,其作用是平衡函数间隔和误分类点的个数,根据实际问题做调整。式(16)的两个不等式约束是去掉绝对值的结果,如式(17)和(18)所示。

约束最优化问题经常是利用拉格朗日的对偶性(Lagrange duality),将原始问题转化为对偶问题从而来得到原始的解。 现引入拉格朗日乘子,得到拉格朗日乘子式如(19)式所示

式中,C=a1i+u1iand C=a2i+u2i因为拉格朗日乘子 a1i≥0,a2i≥0。所以 0≤a1i,a2i≤C,又 g1i和 g2i不能同时存在,所以 a1i×a2i=0,因此支持向量回归的同柔性边界 KKT 条件达成了,如式(20)-(22)所示

将得到的支持向量带入求解得问题最优解,如式(23)所示

由此求得回归方程,如式(24)所示

2.2 核函数
SVR 采用核函数技巧,通过非线性变换将非线性问题转换为线性问题来进行求解。 核函数的定义:设X 是输入空间(欧式空间Rn的子集或离散集合),又设H 为特征空间(希尔伯特空间),如果存在一个从 X 到 H 的映射 φ(x),使得对所有 x,z∈X,函数 K(x,z)满足条件 K(x,z)=φ(x)·φ(z),则称 K(x,z)为核函数,φ(x)为映射函数,其中,φ(x)·φ(z)为 φ(x)与 φ(z)的内积。因为直接计算 K(x,z)比较容易,所以在预测问题中,只定义K(x,z),而不具体定义φ(x),在特征空间中隐式的进行学习。
文中的地铁站客流量流预测问题采用多项式核函数(polynomial kernel function),如式(25)所示

对应的支持向量机是一个p 次多项式回归器。 因此,回归决策函数就如(26)式所示

3 仿真实验
3.1 影响因素选择及数据预处理
影响地铁站客流量的因素有很多种,包括天气状况,周末节假日,大型活动事件以及政策影响等,其中天气状况对交通的影响是直接且立竿见影的,地铁站客流量不例外,其对天气呈现出高敏感性。 因此,文中主要研究的是天气状况,日期以及是否有重大活动对地铁站客流量的影响,具体主要包括是否下雨,空气湿度,风向等。
文中选取的是某大城市2011 年5 月份采集的某地数十个地铁站的客流数据和天气状况特征。在训练之前,对数据进行特征归一化处理,这样做的目的是面对多维特征问题时,相近的特征尺度可以帮助预测算法更快地收敛。特别是对于SVR 模型,分布范围较大或较小的数据会对模型参数产生比较大的影响,除非原始各维特征的分布范围就比较接近,否则必须进行归一化处理。具体的预处理方法是正太标准化处理[13],将所有特征的尺度都尽量缩放到-1 到1 之间,如式(27)所示:

其中:xn是特征数据的平均值;Sn是特征数据的标准差。
同时对一些非连续特征进行独热编码,如是否下雨、该站是否有重大活动以及在一周中的星期几等特征,
3.2 模型调参
将建立的模型和实际数据进行拟合。 当模型复杂度偏低时,拟合误差就会较大,即高偏差欠拟合,对此可通过增加模型复杂度来解决。 比如,采用高阶模型(预测)或是引进更多的特征(分类)等就可避免此类问题产生。而当模型复杂度偏高并且训练数据过少时,就会引起测试误差变大,即高方差过拟合,对此就需要降低模型的复杂度,比如加上正则惩罚项,增加训练数据等。
文中采用交叉验证的方法来解决模型训练过程中高偏差或者高方差问题。 交叉验证(cross validation)是由Seymour Geisser 提出的一种统计学上将数据样本切割成较小子集的实用方法,也叫循环估计(rotation estimation)。 其工作原理是将部分原始数据作为训练集,其余为验证集,用验证集来检验通过训练集得到的模型从而评价模型性能[14],为了降低验证结果的可变性,将原始数据集进行多次划分以得到多组互补子集从而进行多次交叉验证。 交叉验证不仅考虑了模型建立的训练误差,同时也考虑了泛化误差。
交叉验证主要有Hold-Out Method,K-fold Cross Validation (K-CV) 以及Leave-One-Out Cross Validation(LOO-CV)三种方法。 Hold-Out Method 只用将原始数据集进行简单的分组,方法复杂度低且方便实际应用,但是效果较差,因为随机分组会对预测结果产生较大的影响,而且会造成原始数据的重复使用或漏用。 LOO-CV 可以使几乎所有原始数据都参与训练而没有随机性,这样建立的模型更接近实际情况并增加预测可靠性,但是原始数据集数据量过大会增加模型建立的计算复杂度。本文的客流量预测模型采用K-CV 交叉验证法,将原始数据集均分成n 组,每个数据子集分别做一次验证集,其余的n-1 组子集数据作为训练集,利用n 个模型的最终验证集的预测准确率的均值来评估模型性能指标从而有效的避免过拟合和欠拟合[15]。
3.3 结果分析
(1)评价系数
样本数据为N,设定yi(i=1,2…,N)为地铁进站客流量的实测值,fi(i=1,2…,N)为模型对人流量的预测值。 主要通过下面两个指标对预测结果进行评价。

其中决定系数反映了决策制和期望值的接近程度,即模型对变量的描述能力。 0<R2≤1,R2的值越接近1 表示模型的对变量的预测能力越强。
(2)数据选取和描述
选取某大城市总共465 个地铁站,从2011 年5 月1 日到2011 年5 月30 日以分钟为间隔的所有进站客流量,如图1 所示。
(3)数据划分和特征选取:
首先对总体数据进行初步的分析,单独分析某一特征对进站人流的影响,如图2 所示,以星期几为横坐标绘制出人流的变化曲线。

图1 某大城市地铁站进站客流量
可以看到星期对人流的影响是很明显的,在周五和周六的的人流量明显少于其他几天,同样观察得到是否雨天、是否重大活动等离散变量对人流的影响也很显著。 于是考虑将上述变量作为建模特征,并在数据预处理中对以上非连续特征进行独热编码。
初步观察连续特征(所在小时、平均温度、平均湿度等)对入站人流量的影响,如图3 所示,以小时数为横坐标绘制出人流的变化曲线图。

图2 星期-进站人流曲线

图3 小时-进站人流曲线
最后经过观察每一变量对人流量的影响,最终选择建模的特征有:地铁站编号、星期几、小时、平均温度、平均气压、平均湿度、是否重大活动、是否有雨、是否有雾、七天前此刻的人流。
为方便模型调参以及模型检验,把所有数据按照9∶1 的比例划分为训练集、验证集,训练集采用交叉验证的方法对模型进行训练和调参,以达到较好的拟合效果,最后用验证集来检测模型性能。
(4)基本的线性回归模型预测
首先建立基本的线性回归模型,以某一时刻的所有特征为训练样本带入线性回归式中


通过求导公式得到参数的梯度下降更新方程

经过200 次的梯度下降训练,在测试集中得到的预测结果与实际结果如图4 所示。
蓝色曲线是实际的人流量,黄色的是线性回归模型预测的结果,可以看到预测拟合的效果不是很理想,对此分析,原因可能是可能是欠拟合(高偏差),则需要提供更多的训练数据;或者是过拟合(高方差),则考虑增加预测模型的复杂度。 为了进一步分析模型误差的问题,通过交叉验证的方法,将训练集按照5∶1 的比例作为新的训练集和交叉验证集,画出随着样本数增加模型的性能分别在训练集和交叉验证集上的表现图,分别对应平均误差和决定系数两个评价参数,学习曲线如图5 所示。

图4 线性回归预测与实际对比

图5 线性回归模型学习曲线
可以看到无论对于平均误差还是决定系数,验证集和训练集的评价指标已经基本接近,可以判断线性回归预测模型是属于高偏差欠拟合的状态,因此为进一步提高预测精度,需要使用更复杂的非线性预测模型,如SVR 和XGBoost。
针对数据特征的关系,使用的SVR 模型核函数为RBF 核函数,此模型受参数的影响很大,利用交叉验证的方法,寻找最优的错误项的惩罚参数C 和学习率ε。 得到C=10000,ε=0.08。 对比测试集中的预测值和实际值,如图6。
最后使用XGBoost 的方法,作为提升(boosting)方法的一种,XGBoost 不断的训练迭代拟合当前树模型的残差。 利用交叉验证的方法,寻找的最优模型参数:最大树深 max_depth = 11,min_child_weight=2,样本随机采样率subsample = 0.8,得到的预测结果与实际对比如图7。

图6 SVR 预测与实际对比

图7 XGboost 预测与实际对比
表1 可以看到相比最基本的线性回归模型,SVR 和XGBoost 的模型的预测性能都有很大的提高,其中XGBoost 的效果最好,但是同时XGBoost 的模型也最复杂,调参和训练过程更加耗时,SVR作为一种调参简单易于训练的基本模型也有其优势。

表1 评价系数对比
4 结束语
交通大数据具有体量大、种类多、价值丰富等特征,其在智慧城市建设背景下,通过相互作用和关联为城市交通管理提供更大的可能,并且从以往杂乱无章的管理方式中解脱出来。 交通大数据应用的关键是数据关联性研究,文中对地铁站交通与天气因素的相互关联属性进行分析挖掘。
文中基于某大城市地铁站客流量统计大数据以及天气状况(如雨天、雾天、平均温度以及平均湿度等)等特征构建了XGBoost 和SVR 的地铁站客流量模型,采用特征归一化进行数据预处理和交叉验证的方法调整模型参数来提高建模精度。 验证结果表明,梯度提升决策树和支持向量机两种模型的地铁客流量均取得了较好的预测效果,预测准确率分别为82.5%和54.5%,均优于传统的预测模型。
