风场对明渠输水工程水位的影响及快速预测研究
2020-01-02郭维维
郭维维,龙 岩
(1.山西省水利水电科学研究院,山西太原 030002;2.中国水利水电科学研究院,北京 100038)
为解决水资源时空分布不均的情况,需要新建调水工程。据不完全统计,目前全球已建、在建或拟建的大型跨流域调水工程有160 多项[1],这些工程成为当地工业、农业、城市和人民生活的命脉。有些调水工程中,明渠是主要的建筑物。南水北调中线工程全长1 277 km,其中渠首至北拒马河中支南长1 196.505 km,采用明渠输水[2-3]。在明渠输水系统上,有若干个节制闸、分水口、退水闸等建筑物[4],水流直接暴露在外面。如果发生极端天气,如狂风、暴雨等会对渠道内的水位产生影响,因此,研究风场对明渠输水工程水位的影响非常必要。
近年来,许多学者研究风对湖泊及输水工程的影响[5-7],如J.H.Schoen 等[8]研究风对南非圣卢西亚河口的影响;A.M. Razmi 等[9]研究风对日内瓦湖的水流变化规律影响;E.J.Anderson 等[10]研究圣克莱尔湖和圣克莱尔河三角洲的风力和水力流之间的关系;Guo 等[11]研究风对切萨皮克湾驱动环流侧向结构的影响;类宏程等[12]借助于SMS 地表水软件,研究风对南水北调东线工程东平湖输水流场的影响,指出风生流对东平湖湖区流场的影响可以忽略;郭运武等[13]通过风水槽实验,研究风对河道溢油扩展、漂移的影响,提出无论是对于瞬时溢油还是连续溢油,风都能使溢油油膜扩展尺度增加约2倍;张卓等[14]采用三维数值模型研究风应力对水流运动和摩阻特性的影响,指出底部摩阻受风生底流的影响;陈丽萍等[15]分析了风速对水体中挥发性污染物传质的影响,指出风速越大,污染团尾部的浓度分布占据的空间越大。这些研究主要是对风速变化的研究,忽略了风向及风持续时间的影响,因此,研究风对明渠输水工程水位的影响及快速预测十分必要。
本文依据南水北调中线干渠资料,选取典型渠段作为研究对象,构建输水干渠二维水动力模型,综合考虑风速、风向、风源位置及风的持续时间等因素,模拟明渠内闸前水位变化过程,提出在风的影响下最大水位变幅的快速预测公式,并将其结果与实际监测数据作比较研究。
1 数值模拟
1.1 二维水动力模型
忽略地球自转引起的加速度,平面二维水流控制方程包括连续方程与运动方程。
连续方程:

运动方程:
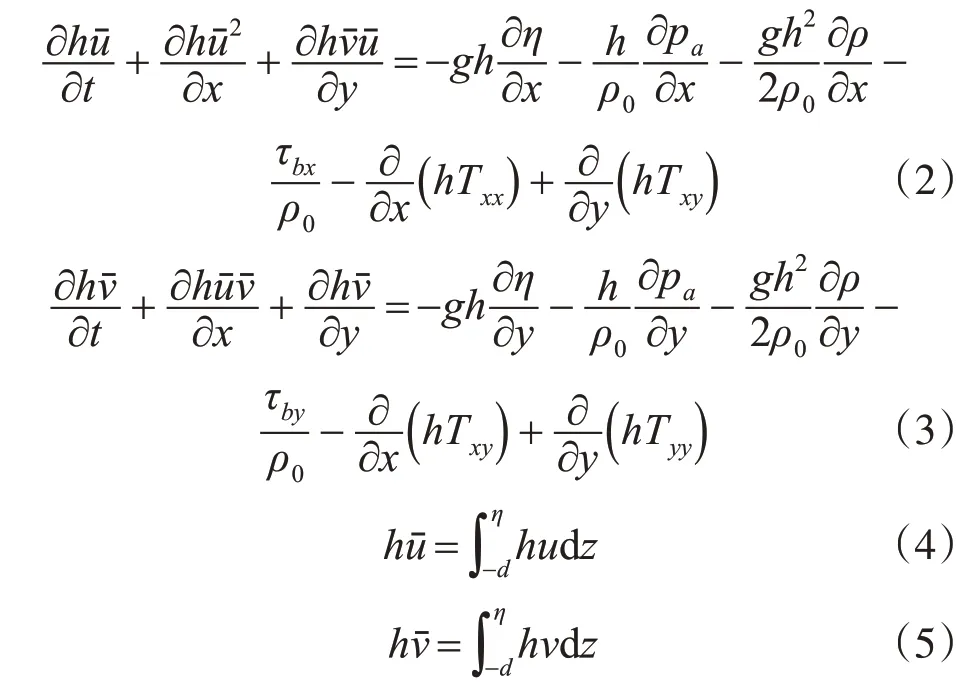
上述式中,h=η+d 为总水深;d 为静止水深;η 为水位;u、v 分别为x、y 方向的流速;Txx、Tyy、Txy为水平粘滞应力项;τbx、τby为床面剪切力;uˉ、vˉ为水深深度方向的平均速度。
1.2 研究对象及模拟工况
在该模型中,风摩擦力可设定为函数。摩擦力是两个风速值的线性内插的函数,如果风速小于最小值或大于最大值,摩擦力则取相应设定的最大或最小值,而不再随风速变化做内插。风摩擦力产生的表面应力大小,由下式得到[16]:

式中,ρa为空气密度;cd为空气中的经验拖拽力;us为渠道表面流速;uˉw=(uw,vw)是海面以上10 m处所测量到的风速。
为研究不同风速、风的持续时间以及风向对闸门前水位的影响,对南水北调中线干渠进行分析,选取典型渠段,设置了31种不同工况。模拟输水明渠的参数如表1 所示,数值模拟工况及参数如表2所示。

表1 模拟渠道的基本参数

表2 模拟工况基本参数
2 结果分析
2.1 不同风速下水位变幅模拟结果分析
模拟风速变化情况下水位变化过程,根据表2中的参数变化范围,设置10 种工况。其中,风持续时间、风向与水流的夹角和模拟时间保持不变,分别为5 h、0°和82 h,风源位置以1 km 为间隔,在1~9 km变化;风速分别为3,6,10,14,18,20,24,28,32 m/s 和36 m/s。对数值模拟结果进行分析后得出:在相同风速下,离风源位置越近,最大水位增幅就越大,风源距离的增加和风速增加的效应刚好相反(见图1(a));在风源位置固定的情况下,风速越大,最大水位增幅也越大(见图1(b))。

图1 不同风速下最大水位增幅变化
2.2 不同风持续时间下水位变幅模拟结果分析
在研究风持续时间对水位的影响过程中,根据表2 中的参数变化范围,设置9 种工况。其中,风速、风向与水流的夹角和模拟时间保持不变,分别为36 m/s、0°和82h,风源位置以1 km 为间隔,从1~9 km 变化;风持续时间分别为:2,5,10,24,30,36,48,60 h和72 h。对数值模拟结果进行分析,结果如图2 所示。风的持续时间对水位变幅的影响很小,误差小,最大偏差为9.83%,因此认为风的持续时间对水位变幅的影响可以忽略不计。

图2 不同风持续时间下水位变化
2.3 不同风向下水位变幅模拟结果分析
在研究风向对水位的影响过程中,根据表2 中的参数变化范围,设置14种工况。其中,风速、风持续时间与模拟时间保持不变,分别为20 m/s、5 h 和82 h,风源位置以1 km 为间隔,从1~9 km 变化;风向与水流的夹角从0°到225°以15°为间隔进行划分。对数值模拟结果进行分析,结果如图3 所示。其中,南风表示β=0°,西北风表示β=45°,北风表示β=180°,东南风表示β=225°。从图4中可以看出,南风和北风下水位变幅值一致,西北风和东南风下的水位变幅一致,即风向与水流方向的夹角位于0°到180°之间的水位变幅与夹角位于180°到360°之间的水位变幅互为相反数。提取风向与水流的夹角β位于0°到180°之间的数值模拟结果,对其进行提炼,得到不同风向下水位最大变幅变化,如表3 所示。从表3 可以看出,随着夹角的增大,水位增幅变小;当夹角为90°时,水位变幅很小;但是当夹角大于90°时,水位下降,而且水位下降值与0°到90°的增幅相同。

图3 不同风向下水位变化过程

表3 不同风向下水位变化情况
基于此,将风速为20 m/s,风向与水流的夹角β位于0°到360°之间的最大水位变幅进行对比,如图4所示。从图4可以看出,整个水位变幅是关于夹角β=180°对称,而0°到90°为最大水位变幅的一个周期,因此0°到360°之间的最大水位变幅可以用式(7)表示。
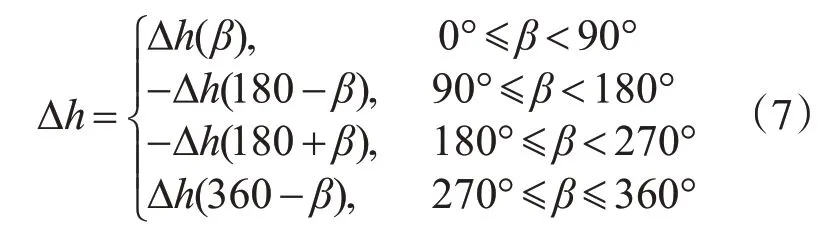
式中,Δh为最大水位增幅,cm。
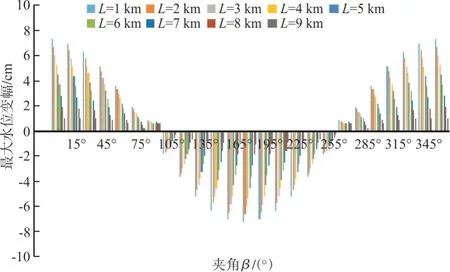
图4 不同风向下最大水位变幅
2.4 风对水位影响的快速预测
通过对不同风速、风的持续时间以及风的方向对闸门前水位的影响研究可知,风的持续时间对最大水位变幅影响很小,且最大水位变幅随风速的增加而增加,随风源距离的增加而减小,同时风向与水流的夹角在0°到90°为最大水位变幅的一个周期。因此分析一个变化周期内最大水位变幅的规律,可以得到风对明渠输水工程最大水位变幅的预测公式:
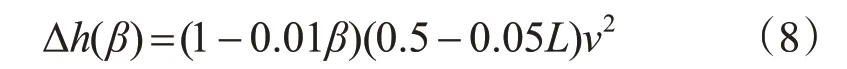
式中,Δh(β)为夹角在0°到90°的最大水位增幅,cm;β为风向与水流的夹角,0°≤β≤90°;L为风源距闸门的距离,km;v为风速,m/s。
2.5 结果验证
2018 年2 月23 日18:00 至2 月24 日18:00,南水北调中线邯郸管理处监测到沁河节制闸闸前水位变化如图5 所示。从图5 可以看出,闸前水位由90.60 m上涨到90.69 m,最大水位增幅为9 cm。
通过气象调查可知,当天为3级北风,风速约为5.1 m/s,风向与水流的夹角β=320°,风源距离沁河节制闸大概1 km。将数据代入式(7)和式(8)中,计算得到最大水位增幅为9.33 cm,与实际值的相对误差为3.66%,误差很小,说明最大水位预测公式对明渠输水工程适用性比较强。


图5 沁河节制闸闸前水位变化
3 结 论
本文主要研究的是风对闸前水位的影响以及风下最高水位快速预测。以南水北调中线干渠资料为基础,通过改变风的条件,利用二维水动力模型研究不同风速、不同风持续时间、不同风源位置以及不同风向下明渠输水工程中闸前水位变化规律及风变化下最高水位快速预测公式,结果表明:
(1)在相同风速下,离风源位置越近,最大水位增幅就越大,风源距离的增加和风速增加的效应刚好相反;在风源位置固定的情况下,风速越大,最大水位增幅也就越大;
(2)风的持续时间对最大水位变幅影响很小,最大偏差为9.83%;
(3)随着风向与水流方向的夹角增大,水位增幅变小,当夹角为90°时,水位变幅很小,但当夹角大于90°时,水位下降,且下降值与0°到90°的增幅相同;
(4)风向与水流的夹角β位于0°到360°之间,整个水位变幅关于夹角β=180°对称,而0°到90°为最大水位变幅的一个周期;
(5)将实际监测的结果和快速预测公式计算结果进行对比,其误差为3.66%,说明最大水位预测公式对明渠输水工程的适用性较强。
