基于改进DIN模型的土压平衡盾构土舱压力计算方法及适用性分析

宋兴海，陈 行，郭治岳，陈文宇

（1.河北水利电力学院土木工程学院，河北沧州 061001；2.四川省公路规划勘察设计研究院有限公司，四川成都 610041；3.西南交通大学土木工程学院，四川成都 610031）

城市地铁隧道施工时环境保护很关键。对于土压平衡盾构，合理控制土舱压力能有效降低对隧道围岩的扰动，减小对地面建（构）筑物的影响［1］。成都市区位于成都平原东部，下伏基岩主要为白垩系上统灌口组（K2g）泥岩，其上主要分布有5～30 m 的第四系沉积层［2］。地铁隧道埋深变化较大，经常穿越上覆土层与下伏泥岩，导致掌子面水土压力变化较为复杂。传统的土压力理论有全土重理论、郎肯土压力理论、太沙基理论、普氏理论等［3-4］。但这些方法目前仍存在一些问题，例如深埋与浅埋的分界线难以确定［5］，没有考虑水压力变化对侧向土压力的影响等，因此不适用于成都地层条件连续变化的情况。

本文结合成都地区的地质情况，探讨在土压平衡盾构土舱压力计算中太沙基理论与DIN 模型的适用性。根据盾构进入泥岩后的水土压力变化对DIN 模型进行改进，并研究改进的DIN 模型在成都地区的适用情况。

1 土舱压力计算模型

1.1 传统土压力理论

土压平衡盾构作业时土舱内的土压力基本等于掌子面横向土压力［6］，深埋隧道需要考虑自然拱效应。传统土压力理论中常用的太沙基公式为

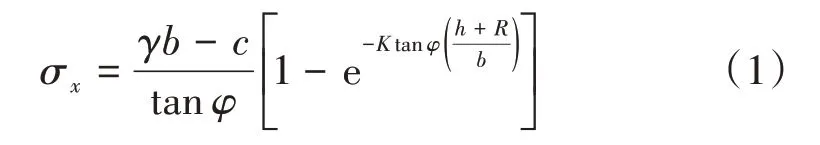
式中：σx为土舱压力；K为掌子面土层的静止侧压力系数；γ为上覆土层平均重度；c为土体黏聚力；φ为土体内摩擦角；h为隧道埋深；R为隧道半径；b为自然拱的半跨度，b=R+Rtan（45°-φ/2）。

太沙基公式仅适用于深埋隧道，埋深较浅时通常使用全土重理论。深埋与浅埋的分界线目前在规范中仍没有统一的界定［5］。同时，传统的土压力理论没有系统地考虑水压力的变化，仅在弱透水地层中对水头进行折减，往往过于保守，不适用于隧道埋深连续变化时盾构土舱压力计算。

1.2 德国工业标准DIN 4085土压力理论

德国工业标准DIN 4085 中采用理论分析与数理统计的方法得到了土压力与隧道埋深的关系式［7-8］。其中，土舱压力σx的计算公式为

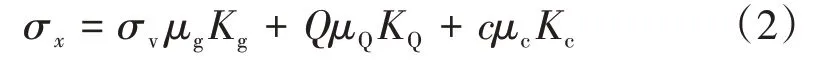
式中：σv为竖向土压力，σv=γh；Q为地面附加压力；Kg，KQ，Kc分别为土体自重、附加压力和土体黏聚力的侧压力系数；μg，μQ，μc分别为土体自重、附加压力和土体黏聚力的形状系数，μg与μQ相等，取值主要与隧道直径和计算点埋深有关。

根据标准中给出的自重系数推荐取值表［7］，拟合得到其计算公式为

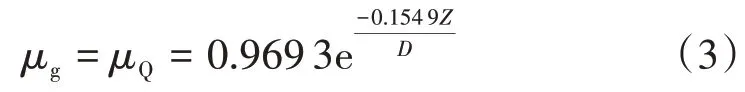
式中：Z为计算点埋深；D为隧道外径。

DIN模型主要考虑了上覆土重、地面附加压力、土体黏聚力对隧道掌子面土压力的影响。土压力随埋深连续变化，但这种方法也没有考虑不同地层中水压力变化对掌子面土压力的影响，在高水位地区适用性有限。

2 成都市天府新区高水位环境土舱压力计算方法

2.1 成都市天府新区地质特点

成都平原在构造上具有地堑式压陷盆地的特点，盆地内主要是第四系不同成因的松散堆积物［9］。由于地壳构造作用，第四系地层从西北的龙门山向东南的龙泉山逐渐变薄，在西部的犀浦尚有100 m 厚度，在成都中心市区厚10～25 m，在龙泉山西侧仅有数米［10］。

成都市地铁建设主要集中在中心市区与东南的天府新区［11］。地下水位在2～10 m，第四系地层厚约5～25 m，主要由粉质黏土、粉土、粉细砂、砂卵石等构成，下伏基岩为泥岩。地铁隧道主要穿越砂卵石地层与泥岩地层。砂卵石及其上覆砂土层的渗透性较强，在计算砂卵石地层中盾构的土舱压力时应采用水土分算的方式。泥岩地层属于渗透性较差的地层，但若隧道埋深较浅，盾构与砂卵石地层之间的泥岩地层受到盾构掘进扰动渗透性增强，因此不能完全将泥岩看作不透水地层，如图1。其中：h1为砂卵石层及其上覆砂土层厚度；h2为隧道顶面泥岩层厚度，即渗流长度。

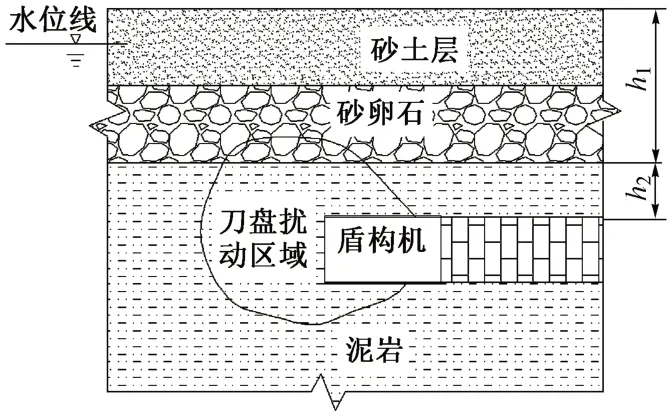
图1 成都市天府新区地铁隧道所处地层

2.2 泥岩地层中水压折减

在泥岩地层中，地下水流经土体时受到土体的阻力而产生水头损失。若隧道埋深较深，水头完全转化为土体竖向有效应力，即几乎不发生渗流，这种情况下可以采用水土合算的方式计算土舱压力［12］。若隧道埋深较浅但仍处于泥岩地层中，此时泥岩中会出现明显的渗流现象，则需要采用水土分算的方式计算土舱压力。由于渗流会造成水头损失，水压力应进行一定的折减，则采用水土分算的DIN 模型土舱压力公式为

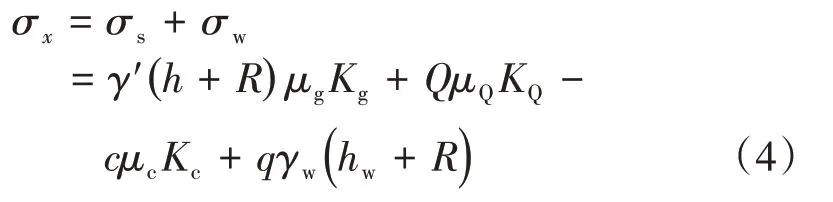
式中：σs为掌子面土压力；σw为掌子面水压力；γ′为土体平均有效重度（即上覆土层的加权平均重度，水位线以上取天然重度，水位线以下取浮重度）；q为水头折减系数；γw为水的重度；hw为地下水位距刀盘顶部的垂直距离。

式（4）中考虑了地下水渗流造成的水头损失，但渗流也会产生渗透力，渗透力将转化为土体竖向有效应力，因此考虑渗透力后DIN模型土舱压力公式为

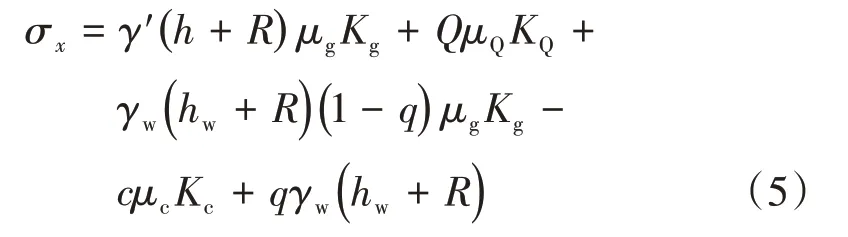
水头折减系数q是一个经验数值，其与地层的渗透性和渗流长度（图1中的h2）有关。通过对成都地铁部分工程的统计分析，在渗流地层为泥岩地层时，q的推荐取值见表1。

表1 q的推荐取值

3 改进的DIN模型效果分析

3.1 3种土舱压力理论公式对复合地层的适用性

成都市天府新区地铁隧道穿越的地层是典型的砂卵石和泥岩组成的复合地层。以成都地铁18 号线盾构区间标准段隧道断面为例，盾壳直径8.6 m，管片外径8.3 m，内径7.5 m。天府一街砂卵石层及其上覆砂土层厚度h1为14 m，地下水位距地面5 m。分别采用传统土压力理论，DIN 模型和改进的DIN模型计算土舱压力。传统土压力理论中以2倍洞径D（即16.6 m）为深浅埋隧道分界。浅埋隧道采用全土重理论计算，深埋隧道采用太沙基理论计算。传统土压力理论与DIN 模型在砂卵石层及其上覆砂土层中采用水土分算，刀盘顶部进入泥岩后采用水土合算。改进的DIN模型采用式（5）计算，水头折减系数按表1取值。

计算所得土舱压力与埋深的关系见图2。可以看出：传统土压力理论在深浅埋交界处和砂卵石地层与泥岩地层交界处的计算结果不连续，在校核结构安全性时可以取最大值来保证安全性，但土舱压力设定值的计算结果出现突变，明显不符合地下水压力和土压力的变化规律。DIN模型在砂卵石地层与泥岩地层交界处的计算结果也存在不连续的问题，而改进的DIN模型考虑水压力连续变化的影响，得出的结果连续性较好，更适用于土舱压力的计算。

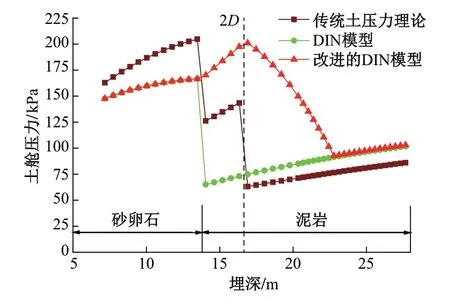
图2 3种理论公式计算结果对比

3.2 改进的DIN模型计算结果与实测值的对比

以成都地铁18号线天府一街的实测数据［13］为例，使用本文改进的DIN 模型计算土舱压力，并与实测值进行比较，见图3。由于地层的不确定性以及现场的人为调整，实测值的离散性较大，因此使用一元多次方程对实测数据进行拟合。

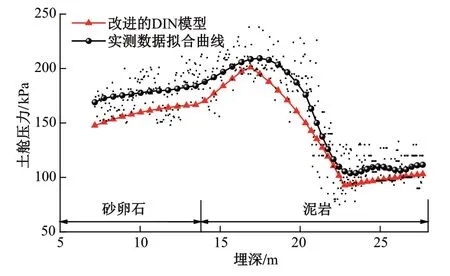
图3 改进的DIN模型计算的土舱压力与实测值对比

由图3可知：计算结果与实测值的整体平均误差为10.5%，精度满足盾构土舱压力设定值要求。这是因为改进的土舱压力计算公式综合了水土分算与水土合算的特点，同时考虑了盾构进入泥岩地层后水压力变化的连续性，使计算结果连续，实用性更强。

3.3 成都西部盾构隧道土舱压力3种理论计算结果对比

成都西部温江区的第四系沉积物厚度较大，主要以砂卵石为主。其地质情况与天府新区不同，地铁隧道几乎全部处于砂卵石地层中。以成都地铁4号线西延线为例，地铁隧道外径为6 m，埋深4～28 m，地下水位距地表3.5 m。分别采用全土重理论，太沙基理论，改进的DIN 模型计算土舱压力，并与实测值对比，见图4。

由图4可以看出：当埋深小于9 m 时，由于砂卵石地层没有黏聚力以及上覆土层厚度较小，基本没有产生土拱效应，改进的DIN 模型与太沙基理论的计算结果偏小，全土重理论的计算结果更接近实测数据；当埋深超过9 m 后，全土重理论的计算结果偏大，改进的DIN模型的计算结果更接近实测数据。

结合以上分析可以看出，改进的DIN 模型不仅适用于成都市天府新区盾构隧道穿越砂卵石和泥岩复合地层的情况，也适用于成都西部盾构隧道穿越砂卵石地层的情况，但当埋深小于隧道外径1.5D时，应对其计算结果进行修正。

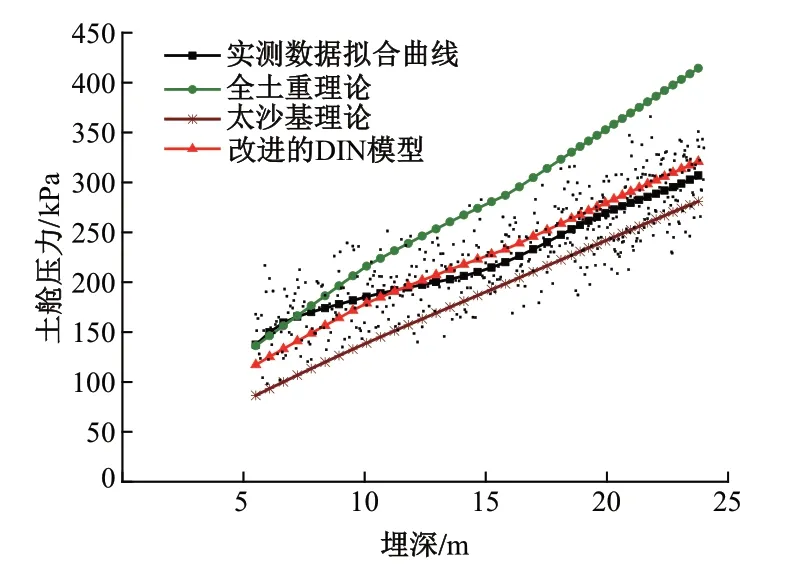
图4 3种土压理论计算结果与实测值对比

4 结语

土舱压力理论计算值是调控土舱压力的重要参考依据之一，传统的全土重理论和太沙基理论计算得到的结果连续性较差。在德国工业标准提出的DIN模型中加入渗透力的影响和静水压力折减，考虑了地下水压力连续变化，最后得出的公式较为适用于地铁隧道穿越透水地层与不透水地层分界的情况。

本文结合成都市区的工程地质特点，通过数理统计给出了采用改进的DIN 模型计算土舱压力时水头折减系数的推荐取值，并通过实例计算发现改进的DIN模型在浅埋砂卵石地层中计算值偏小。